Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

13 Unconventional Superconductivity in Novel Materials 701

Table 13.6. Crystallographic data and T

for some organic metals based on the donor molecules TMTSF and ET. Z is the

number of formula units per unit cell. For T

the usually stated values are given independent from the experimental de-

termination. The actual thermodynamic values may differ slightly. For the ET-based compounds the out-of-plane lattice

parameter is underlined

Compound sp-gr. a(Å) b (Å) c(Å) ˛(

◦

) ˇ(

◦

)  (

◦

) ZT

(K)

(TMTSF)

1 7.297 7.711 13.522 83.39 86.27 71.01 1 [404] 0.9

(TMTSF)

ClO

1 7.266 7.678 13.275 84.58 86.73 70.43 1 [430] 1.2

ˇ-(ET)

1 6.615 9.100 15.286 94.38 95.59 109.78 1 [431,432] 1.4

ˇ-(ET)

IBr

1 6.593 8.975 15.093 93.79 94.97 110.54 1 [433] 2.8

-(ET)

/c 16.387 8.466 12.832 90 108.56 90 2 [434] 3.5

-(ET)

Cu(NCS)

16.256 8.456 13.143 90 110.28 90 2 [435] 10.4

-(ET)

Cu[N(CN)

]Br Pnma 12.949 30.016 8.539 90 90 90 4 [391] 11.5

-(ET)

Cu[N(CN)

]Cl Pnma 12.977 29.977 8.480 90 90 90 4 [392] 12.8

˛-(ET)

KHg(SCN)

1 10.082 20.565 9.933 103.70 90.91 93.06 2 [436] –

˛-(ET)

Hg(SCN)

1 10.091 20.595 9.963 103.67 90.47 93.30 2 [437] 1.1



-(ET)

1 9.260 11.635 17.572 94.69 91.70 103.10 2 [438] 5.2

this value was reported in [388] for a pressure of 12 kbar. A pressure of ∼ 6 kbar is however sufficient

to suppress the SDW state and enable superconductivity with T

≈ 1.1 K. See, e.g., [439,440]

at a pressure of ∼ 0.3kbar

recently superconductivity with T

≈ 100 mK was reported to occur at 2.5 kbar [441]

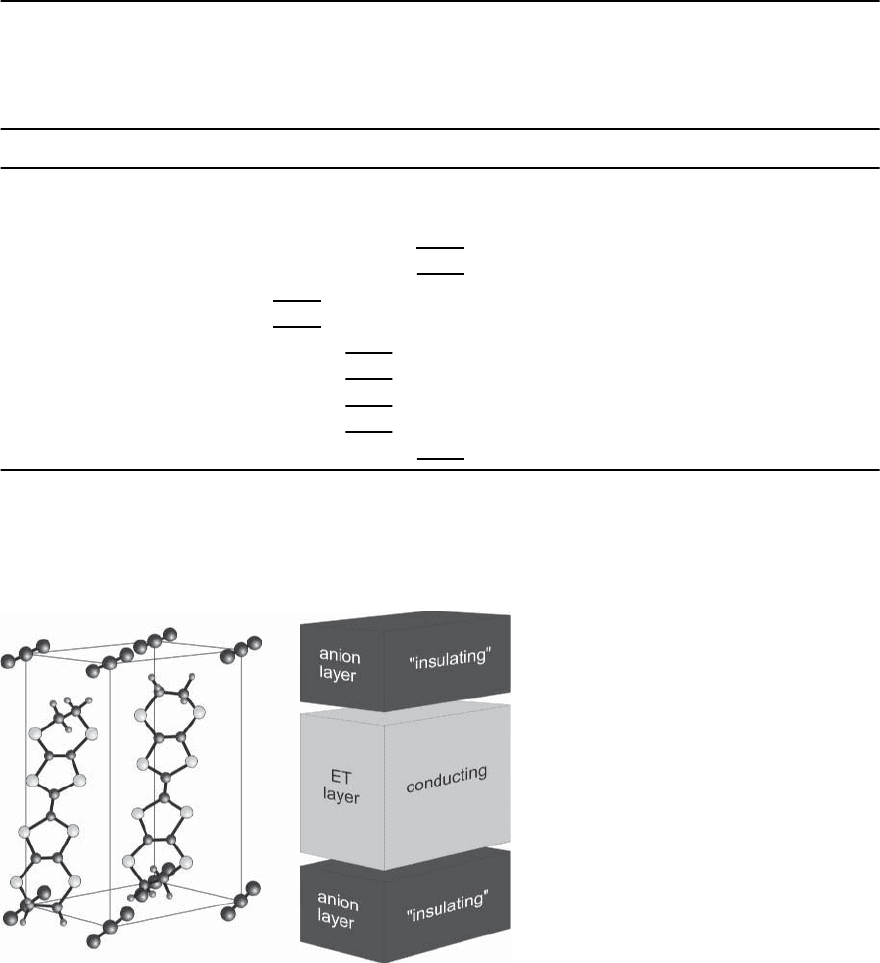
Fig. 13.67. Characteristic layered structure of

the quasi-two-dimensional (2D) organic met-

als, exemplified by the crystal structure of ˇ-

(ET)

. The short distances between the sulfur

atoms ofdifferent ET molecules result in a good

conductivity withintheETlayers.TheETlayers

are separated by the poorly conducting anion

layers, schematically shown on the right side

the charge transfer lead to partially filled molecu-

lar bands, enabling metallic conductivity. The anion

layers are sandwiched between the highly conduct-

ing ET layers.This results in very strong anisotropies

of the physical properties parallel and perpendicular

to the layers. The electrical resistivity perpendicular

tothelayersislargerbyabout3−6ordersofmag-

nitude than for electronic transport within the ET

layers [389,399]. One should mention, however, that

the exact value of this anisotropy is difficult to deter-

702 M.B. Maple et al.

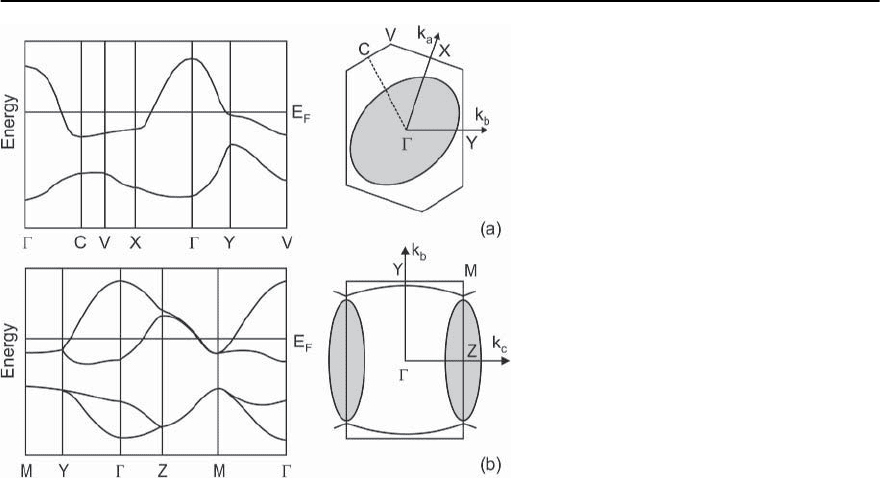
Fig. 13.68. Calculated energy dispersions and

Fermi surfaces for (a) ˇ-phase and (b) -phase

ET salts (after [443,444] and [445])

mine since any dislocation disturbing the in-plane

transport will immediately lead to an enhanced in-

plane resistance [401,442].This 2D structure,which

is also reﬂected in the superconducting properties, is

observed in all ET phases and resembles that of many

layered cuprates, such as Bi

CaCu

8−ı

[396].

Although the layered structure occurs in all ET-

basedsuperconductors,thevarying in-plane packing

motifs of the organic molecules lead to different 2D

electronic structures. The overlap integrals vary con-

siderably depending on whether the ET molecules

are aligned face-to-face or side-by-side [443,444].

The in-plane transfer energies can be obtained from

these overlap integrals that, together with the known

crystal structures, allow the in-plane electronic band

structures to be calculated using the rather simple,

but well-established extended H¨uckel tight-binding

approximation. Two examples of the resulting en-

ergy dispersions and of the in-plane Fermi surfaces

are shown in Fig. 13.68.

For the ˇ phase,one electron per unit cell is trans-

ferred to the anion leaving the highest occupied

molecular orbital half filled. The nearly isotropic in-

plane overlap integrals lead to an almost circular

free-electron-like FS (Fig. 13.68(a)) [443, 444]. The

validity of this result has been verified by measure-

ments of magnetic quantum oscillations and angular

dependent magnetoresistance oscillations [410,446].

Indeed, only one closed orbit with the predicted area

(shaded area in Fig. 13.68(a)) and only slightly more

cornered shape [446, 447] could be reconstructed

from the data.

For the  phase, the resulting FS is almost as sim-

pleasfortheˇ phase. Here, the ET molecules form

dimers where adjacent pairs in the plane are rotated

by approximately 90

◦

with respect to each other.This

doubles the unit cell, resulting in two transferred

electrons on two highest occupied molecular orbitals

(see the dispersion relation in Fig. 13.68(b)). The re-

sulting FS again resembles the free-electron picture

wheretheFScutsthefirstBrillouinzonewithsmall

gaps opening at the zone boundary due to Bragg re-

ﬂections [445]. In fact, for -(ET)

Cu(NCS)

,larger

gaps at the zone boundary are found due to the

lack of a center of symmetry [448].Again, de Haas–

van Alphen (dHvA) and Shubnikov–de Haas (SdH)

experiments confirm the predicted band structures

for the -phasematerialsaswellasformostother

phases. However, the calculated effective masses are

often much smaller than the experimental values,

13 Unconventional Superconductivity in Novel Materials 703

sometimes close to the free-electron value. This is

usually ascribed to the fact that many-body effects

like electron–electron and electron–phonon interac-

tions are typically not included in band-structure

calculations.For moredetails on Fermi-surfacestud-

ies, see the reviews in [410,446,449].

Although the extended-H¨uckel treatment has

been successful in describing the in-plane electronic

band structure of organic metals and superconduc-

tors, it leaves the interlayer band structure unclear.

The large separation of the conducting organic lay-

ers by relatively thick anion layers has led to the

question of whether a real 3D Fermi surface exists

at all. When the interlayer transport is incoherent,

i.e.,when an electron loses its phase information be-

tween successive tunneling processes, no Bloch state

can evolve and the band picture breaks down [450].

Although there is no experimental proof for this sce-

nario, certain experimental features can be utilized

to verify the coherent transport and the existence of

a 3D Fermi surface [450,451].

The most direct test of the 3D nature of the FS,

which even gives a number for the interlayer trans-

fer integral t

⊥

, is the detection of nodes in mag-

netic quantum oscillations.Figure13.69(a) showsthe

dHvA signal for ˇ-(ET)

IBr

. The fast dHvA oscilla-

tions visible in the magnetization can be ascribed to

the closed FS shown in Fig.13.68(a).The existence of

a corrugatedFS,sketched in the inset of Fig.13.69(a),

results in two slightly different extremal orbits for

the field H normal to the layer, leading to the beat-

ing nodes observed in the dHvA signal. At certain

angles  of the field relative to the normal to the

ET planes, only one extremal orbit perpendicular to

H remains and, consequently, no beating node ap-

pears in the dHvA signal. The careful determination

of the angular dependence of these nodes allows a

reliable extraction of t

⊥

[452]. For ˇ-(ET)

IBr

with

a Fermi energy E

≈ 0.11 eV, the transfer integral

⊥

=0.4 meV is obtained.

Although solid proof exists for the coherent mo-

tion of electrons in band or Bloch states in ˇ-phase

ET salts, such evidence is missing for other or-

ganic metals. For example, the magnetization of ˇ



(ET)

shows sawtooth-like dHvA os-

cillations which follow the behavior expectedfor a 2D

metal with fixed chemical potential almost perfectly

(Fig. 13.69(b)) [453]. Furthermore, from the absence

of any beating node in dHvA and SdH oscillations,

which start at about 1.4 T deep in the superconduct-

ing state [454], any possible FS corrugation must be

extremely small. Indeed, additional tests for the ex-

istence of a 3D FS failed for this material [455],mak-

ing it a likely candidate for the 2D metal with inco-

herent interlayer transport envisioned by McKenzie

and Moses [450].Along these lines, deviations from

the conventional Bloch–Boltzmann transport theory

were observed in the interlayer magnetoresistance,

i.e., a field-induced metal-insulator transition was

found [456]. In spite of these highly unusual proper-

ties which contradict Fermi-liquid theory, the inter-

layer resistanceatH = 0 ismetallic overthe whole in-

vestigated temperature range (see Fig. 13.70) and the

measured quantum oscillations are consistent with

an in-plane Fermi liquid. A possible realization of

the FS of ˇ



-(ET)

is depicted in the

inset of Fig. 13.69(b).

For some organic superconductors, such as -

(ET)

Cu[N(CN)

]Br, the interlayer resistivity in-

creases upon cooling, reaching a maximum be-

fore metallic behavior sets in at lower temperature

[389,399]. There were speculations that this might

be caused by antiferromagnetic ﬂuctuations, espe-

cially since NMR measurements of the spin-lattice

relaxation rate 1/T

revealed a maximum in 1/(t

close to the temperature where the maximum in R

was observed (see also the dashed line in Fig. 13.76

below) [457,458].However, as was shown in a recent

thorough study, a significant part of the scattering

contribution giving rise to the anomalous resistiv-

ity maximum is extrinsic in nature [459]. For low-

resistance variants of -(ET)

Cu[N(CN)

]Br, grown

by a different preparation route [459], no resistance

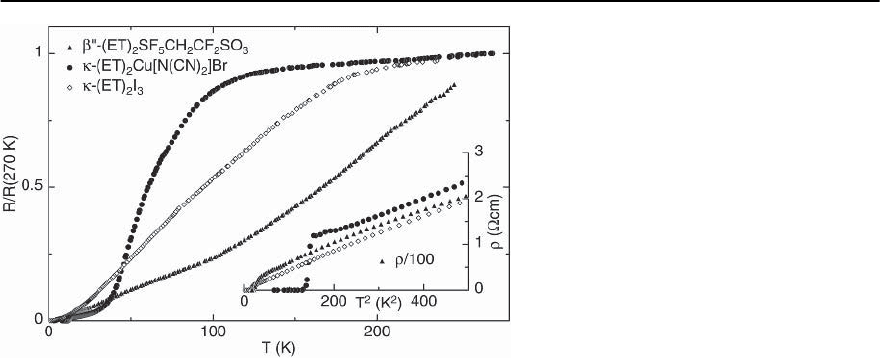
maximum occurs. This metallic behavior all the way

down from room temperature is presented for such

a -(ET)

Cu[N(CN)

]Br sample in Fig. 13.70, where

the metallic resistance for two other organic super-

conductors is shown as well.

At high temperature, there is no generic T depen-

dence forthe differentorganic metals.Towards lower

T, however, the interlayer resistivity can fairly well

be described by  = 

+ AT

(inset of Fig. 13.70).

704 M.B. Maple et al.

Fig. 13.69. (a) de Haas–van Alphen (dHvA) os-

cillations in the magnetization of ˇ-(ET)

IBr

at T =0.4 K. The nodes in the signal are caused

by the slightly corrugated FS perpendicular to

theconducting ETplanes.The schematicsketch

in the inset greatly exaggerates this corruga-

tion.(b) Torque as a function of magnetic field

of ˇ



-(ET)

. The dHvA signal

(open circles in the upper inset) can be de-

scribed almost perfectly by a 2D theory (solid

line in the upper inset)TheFScanberegarded

as ideally 2D (lower inset)

This T

behavior, which is also observed for many

other organic metals [389], is usually taken as a

sign of a well-behaved Fermi liquid where scatter-

ing is dominated by electron-electron interactions.

However, although electronic correlations certainly

are present in these low-dimensional metals, the

wide temperature range over which the T

behav-

ior can be found is not typical. Usually, this tem-

perature dependence of  can only be observed at

very low temperatures. The coefficient A depends on

the strength of the electron–electron interaction and

is roughly proportional to 

,where is the Som-

merfeld coefficient of the specific heat [188]. As dis-

cussed in Sect. 13.3, for narrow-band systems like

heavy-fermion metals, where electronic correlations

are undoubtedly much more dominant than for or-

ganic metals,A/

≈ 10

−5

§ cm(mol K/J)

.Fortran-

sition metals,A/

is even a factor 100 smaller. Using

a Sommerfeld coefficient  ≈ 25 mJ/mol K

derived

from the specific heat of the organic metals (see be-

low), A ≈ 6 × 10

−9

§ cm K

−2

would be expected for

narrow-band metals. This is 6 to 8 orders of mag-

nitude smaller than is actually observed for the or-

ganic metals (A ≈ 4m§ cm K

−2

for the -phase salts

and about 100 times larger for the ˇ



salt). When

using the in-plane resistivity data, A is still at least

two orders of magnitude larger than expected. Thus,

it seems highly questionable to seek the origin of

13 Unconventional Superconductivity in Novel Materials 705

Fig. 13.70. Temperature dependence of the in-

terlayer resistance R,normalizedbyR at 270

K, for three different organic superconductors.

The inset shows the resistivity  as a function

of T

.Notethat for ˇ



-(ET)

has been divided by 100

this T

behavior of the resistivity solely within the

electronic system [460]. Scattering of 2D electrons

at phonons might be the relevant mechanism. Inter-

estingly, a number of other novel superconductors,

including MgB

and the borocarbides, reveal a T

dependence as well, hinting at a possible common

mechanism.

A further point which should be noted is the ex-

traordinarily high interlayer resistivity  of the or-

ganic metals.For -(ET)

Cu[N(CN)

]Br,  ≈ 1 § cm

just above T

, which is about a factor of 10

larger

than for lead at T

.Forˇ



-(ET)

,  is

another factor ∼ 50 larger. The mean-free path de-

rived from these values of  according to the usual

transport theory is much smaller than the inter-

atomic distances.This effect becomes even more pro-

nouncedtowardshigher temperatures.Again onehas

to ask, in analogy to the high-T

cuprates, whether

the interlayer transport can be understood in terms

of the usual Fermi-liquid theory.

13.4.3 Superconducting-State Properties

The organic superconductors, as well as all other

novel superconductors discussed here, are strongly

type-II superconductors. The lower critical fields,

, of the organic superconductors are only a few

mT and the upper critical fields, H

,areintheTesla

range. These fields depend strongly on the direction

of the applied field.For H applied within the planes,

perpendicular to the least-conducting direction, H

often exceedsthePauli paramagnetic limit [16,17].As

will be discussed below in more detail, this is taken

as an indication for triplet pairing in the 1D ma-

terials. For the 2D organic superconductors, on the

other hand, many-body effects seem to explain the

observed moderate H

enhancement.

Above a certain threshold field H

irr

within the

Shubnikov phase, the magnetic ﬂux can move freely

leading to dissipative phenomena and phase dia-

grams similar to those studied in great detail for

the high-T

materials. In spite of their moderate val-

ues of T

, the layered structure and the high purity

of the organic superconductors lead to a large re-

versible range in the mixed state. In contrast to the

high-T

superconductors,the upper critical fields of

the organic superconductors are relatively low and

more experimentally accessible. Thus, we can con-

veniently study the complete superconducting phase

diagrams and the rich physics of the vortex phase.

Indeed, as previously observed in high-T

cuprates,

the first-order vortex-lattice melting transition close

to H

irr

was resolved in two -phase ET superconduc-

tors by means of sophisticated magnetization exper-

iments [461,462].Anothercommon featureobserved

for the highly anisotropic cuprates [463] and the

equally anisotropicET superconductorsis the occur-

rence of Josephson plasma resonances in magneto-

optical experiments [464].

706 M.B. Maple et al.

1D Organic Superconductors

All the known 1D Bechgaard superconductors, ex-

cept for (TMTSF)

ClO

, need pressure above at

least 6 kbar to become superconducting at transition

temperatures around 1 K. The amount of pressure

needed to suppress the insulating ground state de-

pends on the quality of nesting, i.e., on the electronic

energy which can be gained at a Peierls transition. In

other words, a certain degree of two-dimensionality

is necessary to allow superconductivity to appear. In

fact, an almost linear relationship has been observed

between the lattice parameter b (see Fig. 13.63) and

the critical pressure which suppresses the SDW state

and induces superconductivity [465].

A further increase in pressure P results in a rapid

decreaseof T

onthe orderof dT

/dP ≈ 0.1K/kbar.A

decreasing T

with pressure is a common feature in

many conventional superconductors, however, with

a much smaller dT

/dP. This can be explained by

stiffening of the lattice under pressure that results in

an increase of the average phonon frequency. This

lattice stiffening is expected to be especially strong

in soft organic crystals. Since in conventional super-

conductors T

depends sensitively on the phonon fre-

quency, T

decreases.

For the highly anisotropic organic metals, a cor-

respondingly strong directional dependence of the

critical fields is observed. The lowest upper critical

fields are found for H aligned along the c

∗

direc-

tion (H

≈ 0.16 T for (TMTSF)

ClO

) [389]. For

this fieldorientation,orbitaleffects, i.e.,diamagnetic

currents running in the ab



plane, limit H

.Formag-

netic fields along b



and a, this orbital limiting is

largely suppressed due to the short c

∗

-axis coher-

ence length. Consequently, in early experiments up-

per critical fields of ∼ 2and∼ 2.8 T, respectively,

were reported [466].Thisresultwasdiscussed in light

of a possible Pauli-limited H

, suggesting that the

Cooper pairs in the Bechgaard salts are in the sin-

glet state. Neglecting spin-orbit coupling and many-

body effects, the Pauli (or Clogston) limit is given

by H

=(1.85 T/K)T

[16, 17], i.e., H

≈ 2.3 T for

(TMTSF)

ClO

with T

=1.25 K.

Since H

displays a strong anisotropy, an exact

alignment of the field with respect to the princi-

pal axes, a, b



,andc

∗

is required for its correct de-

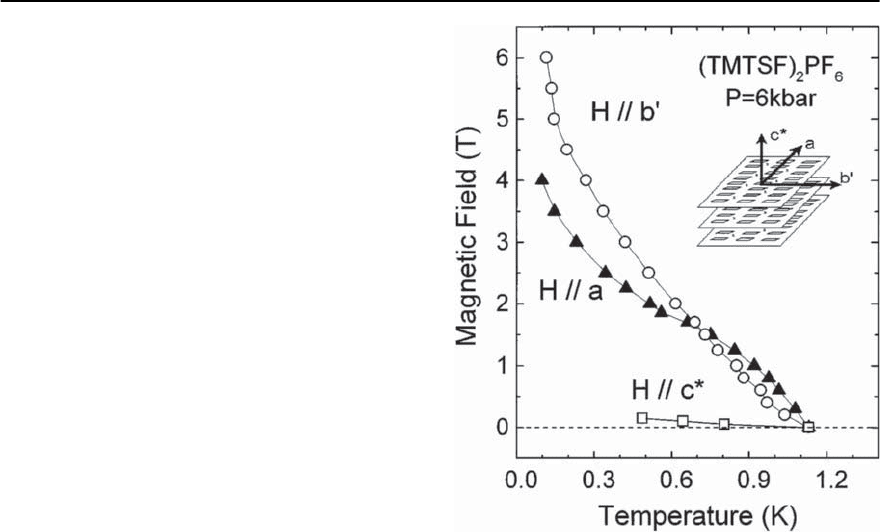
Fig. 13.71. H − T phase diagram of (TMTSF)

at an ap-

plied pressure of 6 kbar for fields aligned along the a, b



and c

∗

directions (see inset)Thedataareextractedfrom

electrical-resistance measurements [439,440]

termination. Indeed, by carefully aligning H. Lee et

al. proved impressively that for (TMTSF)

under

pressure, H

definitely exceeds the Pauli paramag-

netic limit (Fig. 13.71) [439,440]. This occurs for H

oriented along the a direction but even more pro-

nounced for H aligned along the b



direction. For

these field orientations, the orbital motion of the

charge carriers is greatly suppressed due to the weak

interplane transfer.TheH −T phase diagram was ex-

tracted from electrical-resistance data. The validity

of this determination has recently been verified for

(TMTSF)

ClO

utilizing torque magnetization mea-

surements [467]. The observed strong H

enhance-

ment triggered the proposal by Lebed of triplet or

p-wave pairing occurring in the 1D organic super-

conductors [468].

In order to provide further evidence for triplet

pairing,ajointeffortbyseveral different groupstack-

led the challenging task of performing NMR mea-

surements under pressure at dilution-refrigerator

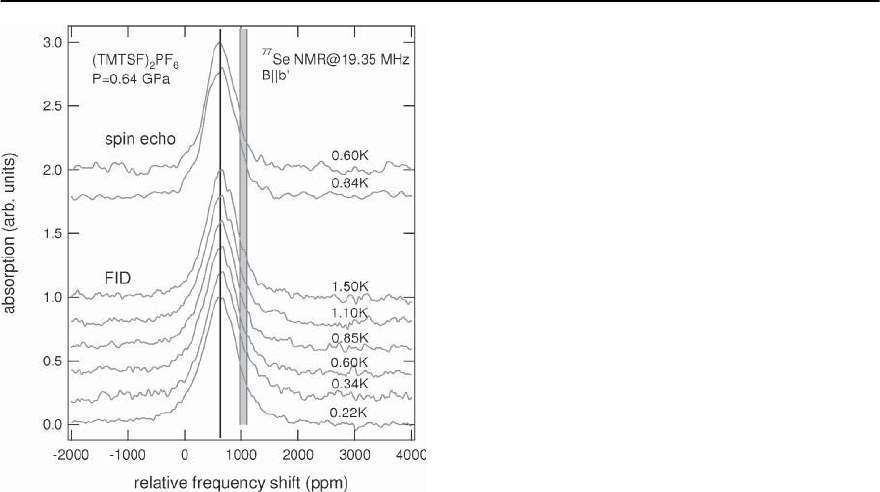
13 Unconventional Superconductivity in Novel Materials 707

Fig. 13.72.

Se NMR spectra below and above T

for

(TMTSF)

with a magnetic field H =2.38 T aligned

along the b



-axis. The center of the NMR peak is virtu-

ally independent of temperature (solid line), whereas the

hashed r egion marks the expected range where it should

occur for a singlet ground state below T

[440,469]

temperatures [469,470].The resulting

Se NMR data

revealed no observable change in the Knight shift be-

tween the normal metallic and the superconducting

state (Fig. 13.72). This provided strong support for

triplet pairing since for singlet Cooper pairs with

antiparallel spins, the Knight shift, which depends

linearly on the electron-spin susceptibility, should

drop rapidly below T

.Indeed,the unchanged Knight

shift observed previously for Sr

RuO

[321] is one of

the primary pieces of evidence for a triplet state in

this superconductor.Stimulated by the experiments

for (TMTSF)

, Lebed suggested a triplet vector

order parameter with the spins oriented along the b-

axis [471].This proposal fitsnicely withthe observed

features that a magnetic field applied along the b



di-

rection cannot destroy superconductivity. It further

predicts a finiteenergy gap over the whole FS,which

is consistent with thermal-conductivity results for

(TMTSF)

ClO

[472]. In another work, spin-triplet

f -wave-like pairing was suggested, which should be

in competition with singlet d-wave pairing [473]. It

should be noted that previous measurements already

showed a strongly enhanced H

for (TMTSF)

AsF

[474]. This and the suppression of superconductiv-

ity by defects and by chemical substitution moti-

vated early suggestions of a possible p-wave symme-

try in the 1D organic metals [475,476].Very recently,

however, the same group that performed the NMR

shown in Fig. 13.72 carefully checked their results.

In (TMTSF)

ClO

they found a clear change of the

Knight shift at low-enough magnetic fields in the su-

perconductingstate[711].This clearlyprovesthesin-

glet nature of the Cooper pairing. It remains a chal-

lenge to understand the high-field zero-resistance

state in the Bechgaard salts where the Knight shift

remains as in the normal state.

Although the experimental data now point to a

singletscenario,noconsensuson thenatureof super-

conductivityin the Bechgaard salts has been reached

[477]. In other theoretical models it was shown that

even conventional s-wave pairing with an appropri-

ate anisotropic orbital momentum may lead to the

critical-field curve shown in Fig. 13.71 [478]. An-

other possibility is an unconventional d-wave state

where the line nodes of the d-wave gap function are

assumed to be eliminated by the anion ordering in

(TMTSF)

ClO

[479].

2D Organic Superconductors

Equally intense and even more controversial is the

discussiononthe nature of the superconducting state

in the 2D organic superconductors.However, before

discussing this issue in more detail some principal

superconducting properties as well as some high-

field peculiarities will be presented.

Supercond u cting Properties

A typical magnetic phase diagram of the 2D

organic superconductors is exemplified for -

(ET)

Cu[N(CN)

]Br in Fig. 13.73. The magnetic field

isappliedperpendicular totheETplanes.H

andH

are obtained from dc-magnetization measurements,

,whereasH

irr

is derived from measurements of

ac susceptibility,

[480,481].The magnetization is

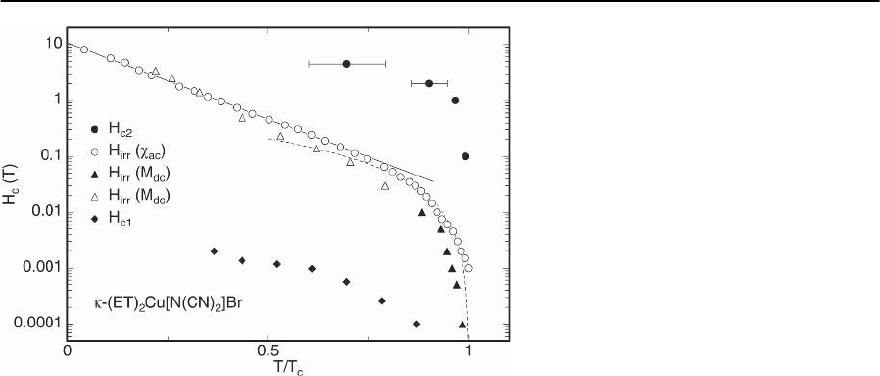
708 M.B. Maple et al.

Fig. 13.73. Temperature dependences of H

, and of the irreversibility field, H

irr

of -

(ET)

Cu[N(CN)

]Br. The data points (•, )are

from [480]. The solid line is an exponential fit,

irr

∝ exp(−AT /T

), at low T.AT

3/2

depen-

dence near T

is denoted by the dashed line

broadened considerably in fields due to supercon-

ducting ﬂuctuations, and a scaling analysis was per-

formed in order to obtain H

(Fig. 13.73) [480],in a

manner similar to that done for the high-T

cuprates.

The lower critical field is often extracted from

the first deviation from perfect diamagnetism. For

the strongly type-II superconductors, like the or-

ganic and high-T

superconductors, however, this

may overestimate H

since above H

,ﬂuxcanonly

penetrate into the sample over a final energy barrier.

This leads to magnetic relaxation effects which be-

come increasingly slow close to H

[399,481]. Since

no time dependence of M is expected to occur in the

Meissner state,H

is defined as the fieldat whichthe

magnetic relaxation vanishes [481].The H

data are

depicted in Fig. 13.73.

For -(ET)

Cu[N(CN)

]Br, an upper critical field

of (12±2) T and a lower critical fieldof(3±1) mT for

T = 0 can be estimated. From these results the ther-

modynamic critical field H

≈ 100 mT, the in-plane

coherence length 



≈ 5 nm, and the Ginzburg–

Landau parameter  ≈ 100 can be derived. With

an average in-plane lattice parameter on the order

d ≈ 1nm, 



/d is approximately 5, which is con-

siderably smaller than the value of ∼10

typical for

pure metals, but comparable to what is found in

high-T

cuprates and other “exotic” superconduc-

tors. The BCS coherence length is given by 

0.18v

≈ 6.7 nm, using an estimate of the

Fermi velocity v

≈ 5.6 × 10

m/s from dHvA data.

With a mean-free path l of 200 to 400 Å, determined

from magnetic quantum oscillations,this organic su-

perconductor is just barely in the clean limit with

l/

≈ 5.In this case,oneexpects 



=0.74

≈ 5nm

which agrees quite well with the experimental value

for 



. For fields parallel to the ET layers, H

is con-

siderably smaller than the earth’s field, making it

nearly impossible to measure [482]. From the esti-

mated value of H

at T = 0 for in-plane field orien-

tations, an approximate interplane coherence length

of 

⊥

≈ 0.5nm can be determined, which is much

smaller than the layer distance of about1.6 nm [396].

For other 2D organic superconductors,similar super-

conducting parameters have been found [402].

The physics of vortex dynamics in type-II su-

perconductors, extensively studied for the high-T

cuprates, has also been investigated in detail for the

organic metals.Abovethe threshold field H

irr

of type-

II superconductors, vortices are free to move and,

therefore, the magnetization is reversible.Below H

irr

the vortices are pinned, resulting in magnetic hys-

teresis, a diamagnetic ac-susceptibility signal, and a

vanishing electrical resistivity. Since the depinning

of the vortices is an activated process, slightly differ-

ent values for H

irr

are obtained depending on the

method used and the criterion applied. Nonethe-

less,the gross temperature and angular dependences

of H

irr

are largely unaffected by these unambigu-

ities [481, 482]. The H

irr

data in Fig. 13.73 show a

clear crossover at T/T

≈ 0.75, independent of the

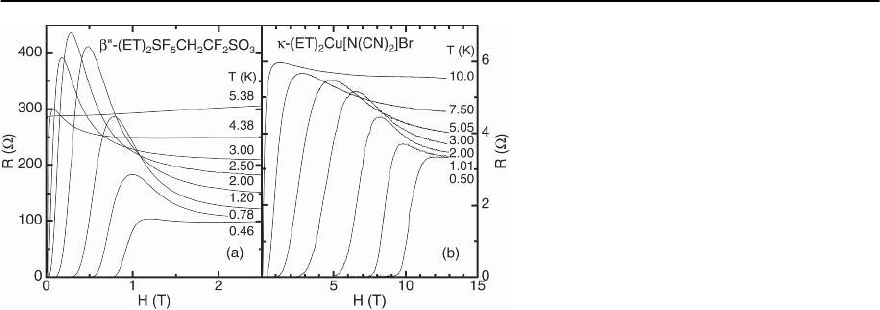
13 Unconventional Superconductivity in Novel Materials 709

Fig. 13.74. The interlayer magnetoresistance

of (a) ˇ



-(ET)

and (b) -

(ET)

Cu[N(CN)

]Br for fields applied perpen-

dicular to the ET planes with strong peaks be-

fore superconductivity occurs

method used to obtain the data. The same behav-

ior has been observed for another -phase organic

superconductor as well [483]. A crossover from 3D

vortex ﬂuctuations to 2D ﬂuctuations is predicted at

amagneticfieldH

≈ 4¥

/

≈ 0.08 T, where

=2.07×10

−15

is the magnetic-ﬂux quantum,

d ≈ 1.6 nm is the interlayer distance, and  ≈ 200 is

the anisotropy parameter estimated from magnetic-

torque measurements for -phase superconductors

[484,485]. This prediction is in excellent agreement

with the experimental value of H

≈ 0.05 T.

Thermally activated 3D vortices are believed to

be responsible for the power-law T dependence of

irr

∝ T

3/2

close to T

(Fig.13.73) [486],whereas the

low-temperature exponential behavior can be under-

stood by the breakdown of proximity-induced su-

perconductivity (see [481] for details). This suggests

that superconductivity is induced in the normal-

conducting anion layers by the superconducting ET

layers. Above a certain threshold field H

irr

for this

proximity-induced superconductivity,thesupercon-

ducting layers are effectively decoupled, and the vor-

tices are weakly pinned 2D objects (pancake vor-

tices). Measurements of the angular dependence of

irr

have verified that in the low-T 2D pinning

regime, H

irr

() exhibits 2D behavior as predicted

by Tinkham for H

() of 2D films [204,487]. Close

to T

, the Lawrence–Doniach model [488] for 3D

anisotropic superconductors describes the data well

[481,483].

In contrast to most conventional superconductors,

the short coherence lengths and large anisotropies

in 2D organic superconductors lead to strong ther-

mal ﬂuctuations close to T

, clearly visible in the

electrical resistivity, the diamagnetic signal, and the

specific heat. Estimates for the width of the tem-

perature regime where thermal ﬂuctuations are rel-

evant can be made using the Ginzburg criterion,

G = |T − T

|/T

∝ (T

−2



−2





−1

⊥

)

.FortheETsu-

perconductors with T

∼ 10 K, a value of G ≈ 10

−2

results,which is comparable to values found for high-

cuprateswhere the larger T

iscompensated by the

correspondingly larger thermodynamic critical field

[395,396,399,402].Forelemental superconductors,

G is of the order 10

−8

due to the much larger coher-

ence lengths. The ﬂuctuation width becomes much

broader in applied magnetic fields, an effect visible

in resistivity and magnetization data,and it has been

studied extensively in both organic and high-T

su-

perconductors [389,396].

One peculiar feature of the 2D organic supercon-

ductors is the occurrence of pronounced peaks in

the interlayer resistance R close to the supercon-

ducting phase boundary (Fig. 13.74), which is be-

lieved to be caused by thermal ﬂuctuations. With

decreasing field, a peak in R is observed before su-

perconductivity sets in. This peak is observed over

a range of temperatures up to T

.Althoughanum-

ber of models have been suggested (see [395,399]for

an overview), a feasible explanation is based on the

ﬂuctuation-induced decrease of the normal density

of states at the Fermi level. Combined with the other

conductivity contributions caused by ﬂuctuations

(Aslamazov–Larkin and Maki–Thompson contribu-

710 M.B. Maple et al.

tions), the observed behavior can be qualitatively re-

produced taking into account the high anisotropy of

the superconductors[395,489,490].Nevertheless,the

origin of this peak effect in the resistance measure-

ments is still not well understood.

Measurements of the physical properties of 2D

organic superconductors in high magnetic fields re-

veal a number of intriguing features. For the or-

ganic superconductor -(ET)

Cu(NCS)

,measure-

ments using a tuned-circuit differential suscep-

tometer revealed a change in the vortex rigidity

at in-plane magnetic fields of about 22 T [491].

This has been suggested to indicate the onset of

a Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state.

This FFLO state is predicted to evolve at high mag-

netic fields when an attractive interaction between

the Zeeman-split spin-up and spin-down quasipar-

ticles leads to pairs with nonzero total momen-

tum [238, 239]. (See also the discussion above for

CeCoIn

.) 2D organic superconductorsare good can-

didates for this scenario when the magnetic field is

applied in plane, which prevents the appearance of

orbital pair-breaking effects. Indeed, very recently

specific-heat measurements revealed clear thermo-

dynamic evidence for the existence of an FFLO state

in -(ET)

Cu(NCS)

[712].

A second fascinating aspect of the high-field work

on organic superconductors is the observation of

field-induced dissipation-less diamagnetic currents

in the organic metal ˛-(ET)

KHg(SCN)

[492,493].

This material is now believed to be in a CDW state

at low temperatures (below 8 K) and fields below

about 23 T [494,495];the material stays metallic with

only a partial nesting of the 1D FS sheets. Early

experimental data were interpreted in favor of a

SDW state (see [410] for details). At higher fields

above 23 T, when the Zeeman splitting deteriorates

the nesting condition for the spin-up and spin-down

bands, a spatially modulated incommensurate so-

called CDW

state is believed to evolve (analogous to

the FFLO statefor superconductors) [496].Itiswithin

this high-field, low-temperature state that proper-

ties resembling a superconducting vortex state ap-

pear.More precisely,a field-induceddiamagnetic sig-

nal [493] and hysteresis loops comparable to the

irreversible region of the Shubnikov phase are ob-

served [492,494,497]. Although Fr¨ohlich supercon-

ductivity has been suggested [401], further justifi-

cation of this proposal is absent. Recently, Harri-

son has suggested that the coexistence of the CDW

with a strongly field-dependent orbital magnetiza-

tion, caused by the Landau quantization of the 2D

Fig. 13.75. Left panel: In-plane field de-

pendence of the resistance R of -

(BETS)

FeCl

for different tempera-

tures from 0.8to5.4K. Right panel:

The H −T phase diagram indicates that

after the suppression of an antiferro-

magnetic insulating (AI) low-field state

with magnetic field, field-induced su-

perconductivity (FISC), referred to in

the text as magnetic field induced su-

perconductivity (MFIS),is observed be-

tween about 18 to 41 T [500]