Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.

Apago PDF Enhancer
707
SAMPLE PROBLEM 11.1
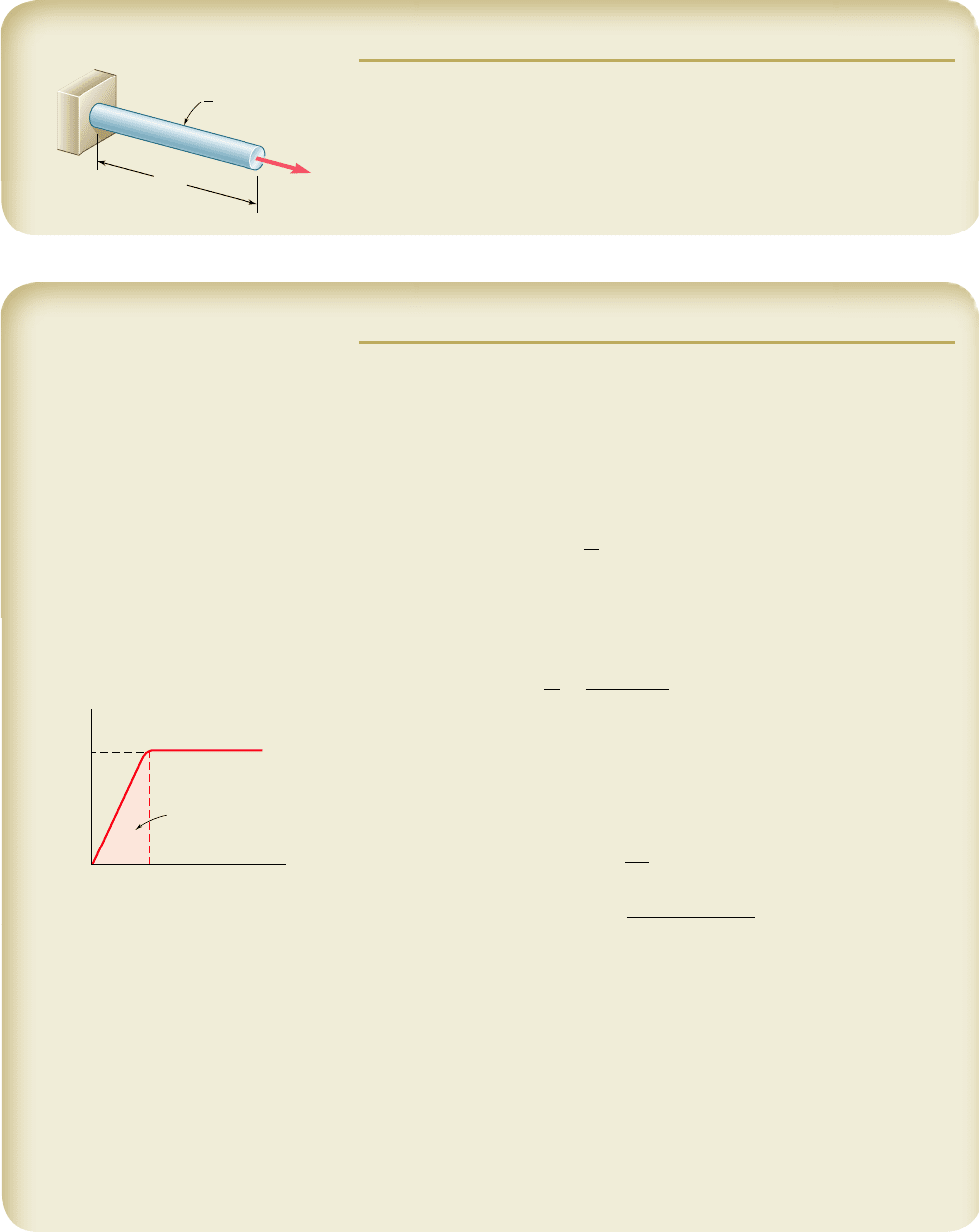
During a routine manufacturing operation, rod AB must acquire an elastic
strain energy of 120 in ? lb. Using E 5 29 3 10
6
psi, determine the required
yield strength of the steel if the factor of safety with respect to permanent
deformation is to be five.
SOLUTION
Factor of Safety. Since a factor of safety of five is required, the rod
should be designed for a strain energy of
U 5 5
1
120 in ? lb
2
5 600 in ? lb
Strain-Energy Density. The volume of the rod is
V 5 AL 5
p
4
10.75 in.2
2
160 in.25 26.5 in
3
Since the rod is of uniform cross section, the required strain-energy
density is
u 5
U
V
5
600 in ?
lb
26
.
5 in
3
5 22.6 in ? lb/in
3
Yield Strength. We recall that the modulus of resilience is equal to
the strain-energy density when the maximum stress is equal to s
Y
. Using
Eq. (11.8), we write
u 5
s
2
Y
2
E
22.6 in ? lb/in
3
5
s
2
Y
2129 3 10
6
p
si2
s
Y
= 36.2 ksi
◀
Comment. It is important to note that, since energy loads are not
linearly related to the stresses they produce, factors of safety associated with
energy loads should be applied to the energy loads and not to the
stresses.
5 ft
B
A
P
-in. diameter
3
4
Modulus of
resilience
Y
bee80288_ch11_692-758.indd Page 707 11/12/10 5:13:17 PM user-f499bee80288_ch11_692-758.indd Page 707 11/12/10 5:13:17 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
SOLUTION
Bending Moment. Using the free-body diagram of the entire beam,
we determine the reactions
R
A
5
P
b
L
x
R
B
5
Pa
L
x
For portion AD of the beam, the bending moment is
M
1
5
P
b
L
x
For portion DB, the bending moment at a distance v from end B is
M
2
5
Pa
L
v
a. Strain Energy. Since strain energy is a scalar quantity, we add the
strain energy of portion AD to that of portion DB to obtain the total strain
energy of the beam. Using Eq. (11.17), we write
U
5
U
AD
1
U
DB
5
#
a
0
M
2
1
2EI
dx 1
#
b
0
M
2
2
2EI
dv
5
1
2EI
#
a
0
a
Pb
L
xb
2
dx 1
1
2EI
#
b
0
a
Pa
L
vb
2
dv
5
1
2EI
P
2
L
2
a
b
2
a
3
3
1
a
2
b
3
3
b
5
P
2
a
2
b
2
6EIL
2
1a 1 b2
or, since (a 1 b) 5 L,
U 5
P
2
a
2
b
2
6EIL
◀
b. Evaluation of the Strain Energy. The moment of inertia of a
W10 3 45 rolled-steel shape is obtained from Appendix C and the given
data is restated using units of kips and inches.
P 5 40
k
ips L 5 12
ft
5 144 in
.
a
5 3
ft
5 36 in
.
b
5 9
f
t 5 108 in.
E 5 29 3 10
6
p
si 5 29 3 10
3
ksi I 5 248 in
4
Substituting into the expression for U, we have
U 5
140 kips2
2
136 in.2
2
1108 in.2
2
6
1
29 3 10
3
ksi
21
248 in
4
21
144 in.
2
U 5 3.89 in ? kips
◀
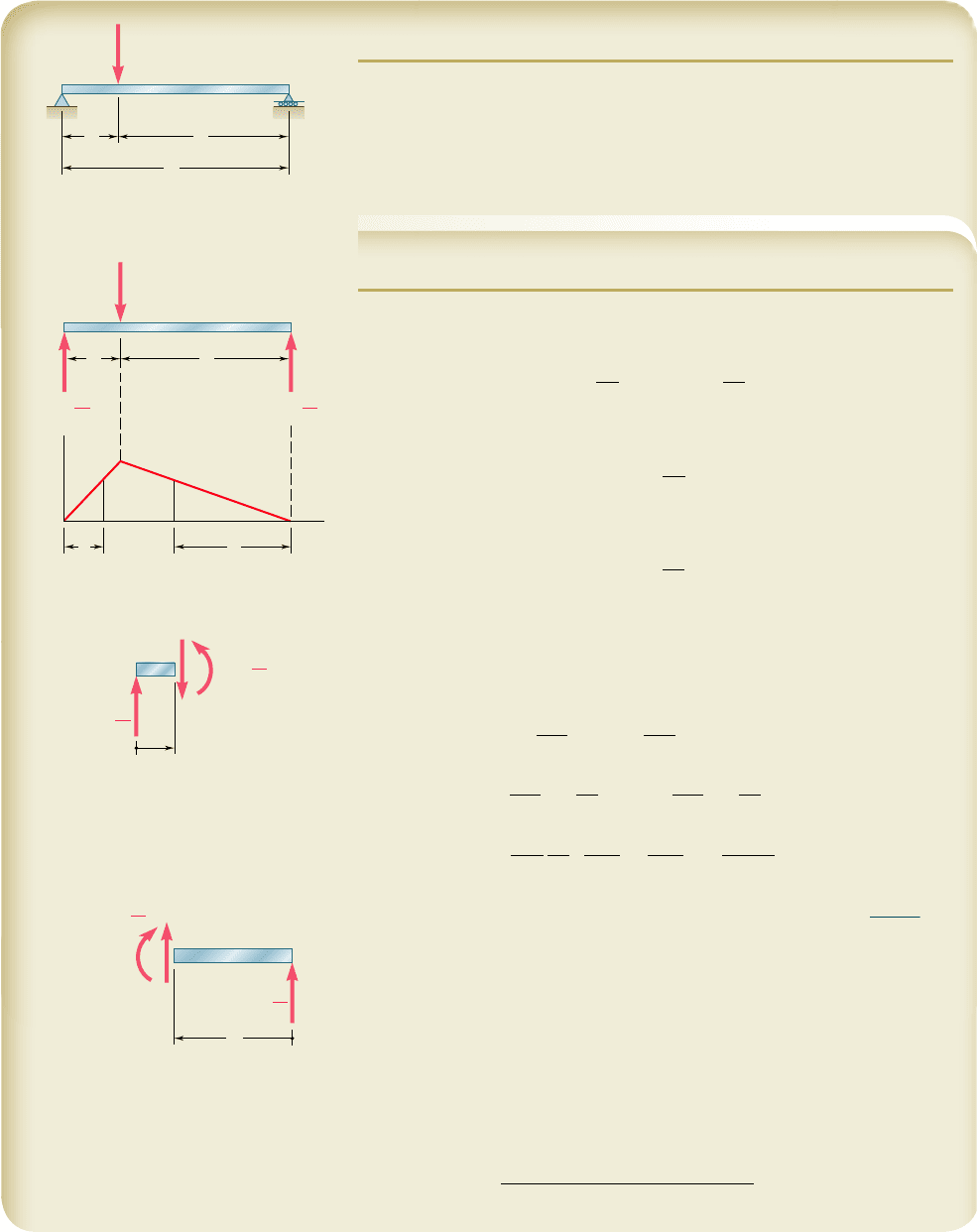
SAMPLE PROBLEM 11.2
(a) Taking into account only the effect of normal stresses due to bending,
determine the strain energy of the prismatic beam AB for the loading shown.
(b) Evaluate the strain energy, knowing that the beam is a W10 3 45,
P 5 40 kips, L 5 12 ft, a 5 3 ft, b 5 9 ft, and E 5 29 3 10
6
psi.
A
L
ab
B
D
P
xv
a
Pb
L
b
D
M
2
R
A
M
1
M
x
AB
Pa
L
R
B
P
x
A
Pb
L
M
1
V
1
x
Pb
L
R
A
From A to D:
v
B
V
2
Pa
L
M
2
v
Pb
L
R
B
F
rom
B
to
D
:
708
bee80288_ch11_692-758.indd Page 708 11/19/10 11:34:03 PM user-f499bee80288_ch11_692-758.indd Page 708 11/19/10 11:34:03 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
PROBLEMS
709
11.1 Determine the modulus of resilience for each of the following
metals:
(a) Stainless steel
AISI 302 (annealed): E 5 190 GPa s
Y
5 260 MPa
(b) Stainless steel 2014-T6
AISI 302 (cold-rolled): E 5 190 GPa s
Y
5 520 MPa
(c) Malleable cast iron: E 5 165 GPa s
Y
5 230 MPa
11.2 Determine the modulus of resilience for each of the following
alloys:
(a) Titanium: E 5 16.5 3 10
6
psi s
Y
5 120 ksi
(b) Magnesium: E 5 6.5 3 10
6
psi s
Y
5 29 ksi
(c) Cupronickel (annealed) E 5 20 3 10
6
psi s
Y
5 16 ksi
11.3 Determine the modulus of resilience for each of the following
grades of structural steel:
(a) ASTM A709 Grade 50: s
Y
5 50 ksi
(b) ASTM A913 Grade 65: s
Y
5 65 ksi
(c) ASTM A709 Grade 100: s
Y
5 100 ksi
11.4 Determine the modulus of resilience for each of the following alu-
minum alloys:
(a) 1100-H14: E 5 70 GPa s
Y
5 55 MPa
(b) 2014-T6 E 5 72 GPa: s
Y
5 220 MPa
(c) 6061-T6 E 5 69 GPa: s
Y
5 150 MPa
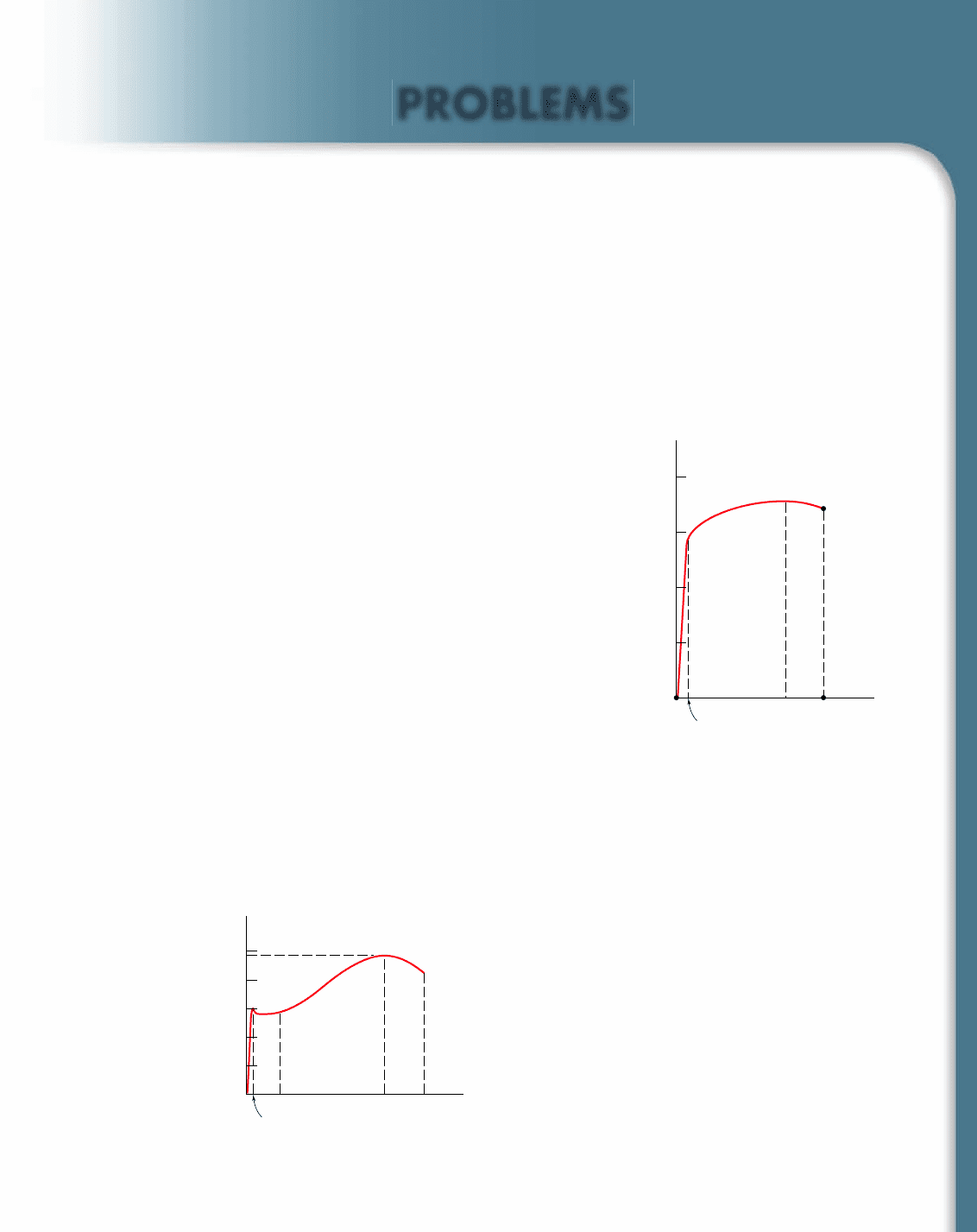
11.5 The stress-strain diagram shown has been drawn from data obtained
during a tensile test of an aluminum alloy. Using E 5 72 GPa,
determine (a) the modulus of resilience of the alloy, (b) the modu-
lus of toughness of the alloy.
11.6 The stress-strain diagram shown has been drawn from data obtained
during a tensile test of a specimen of structural steel. Using E 5
29 3 10
6
psi, determine (a) the modulus of resilience of the steel,
(b) the modulus of toughness of the steel.
(MPa)
600
450
300
150
0.006
0.14 0.18
Fig. P11.5
0.002
0.021 0.2 0.25
100
(ksi)
80
60
40
20
0
Fig. P11.6
bee80288_ch11_692-758.indd Page 709 11/12/10 5:13:32 PM user-f499bee80288_ch11_692-758.indd Page 709 11/12/10 5:13:32 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
710
Energy Methods
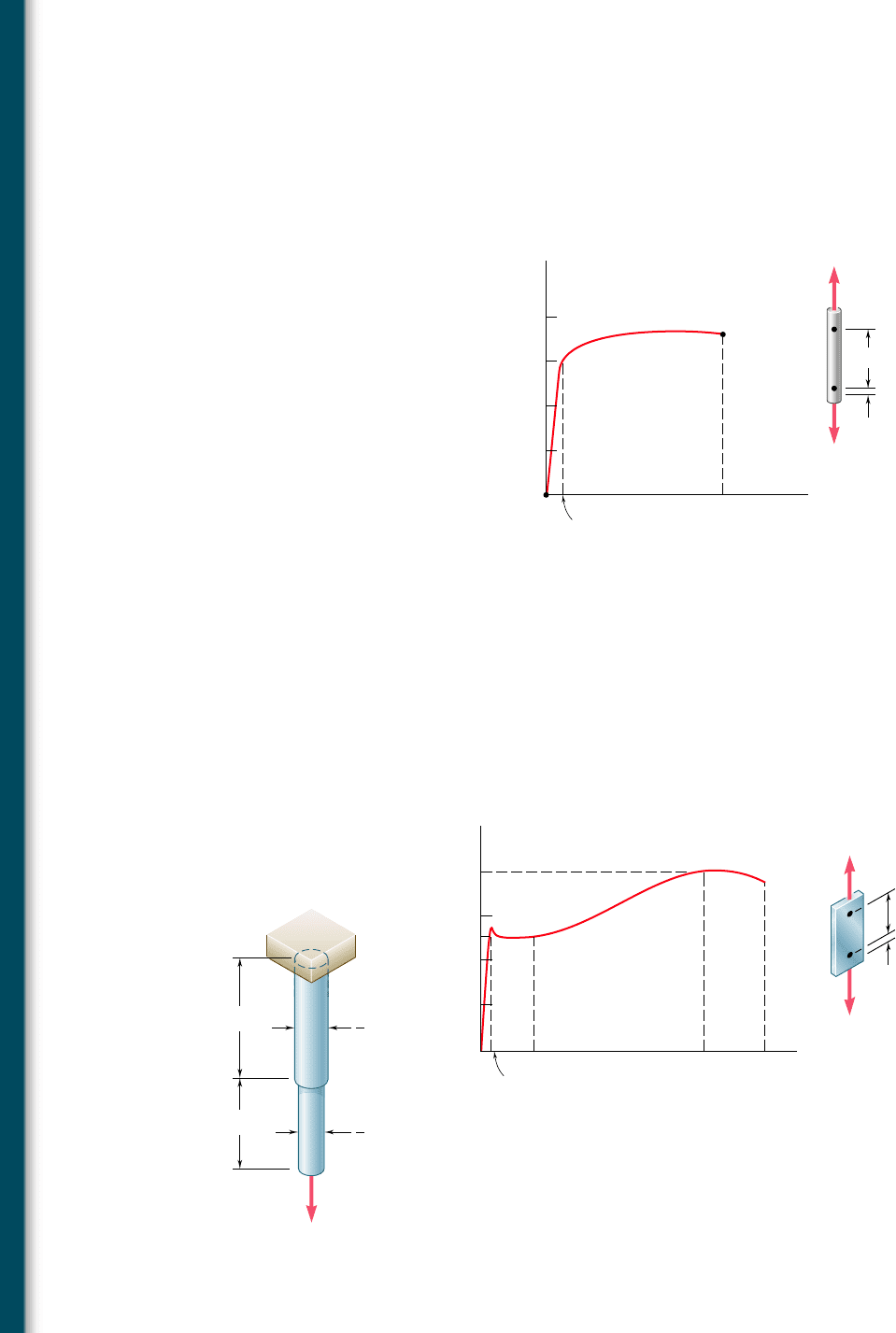
40
30
20
10
0.104
1.85
P'
P (kips)
(in.)
15 in.
P
Fig. P11.7
11.7 The load-deformation diagram shown has been drawn from data
obtained during a tensile test of a 0.875-in.-diameter rod of an
aluminum alloy. Knowing that the deformation was measured using
a 15-in. gage length, determine (a) the modulus of resilience of
the alloy, (b) the modulus of toughness of the alloy.
11.8 The load-deformation diagram shown has been drawn from data
obtained during a tensile test of structural steel. Knowing that the
cross-sectional area of the specimen is 250 mm
2
and that the defor-
mation was measured using a 500-mm gage length, determine
(a) the modulus of resilience of the steel, (b) the modulus of tough-
ness of the steel.
P
B
C
2 ft
3 ft
A
in.
3
4
in.
5
8
Fig. P11.9
0.6
8.6 78 96
P
P'
500 mm
75
100
P (kN)
(mm)
50
25
Fig. P11.8
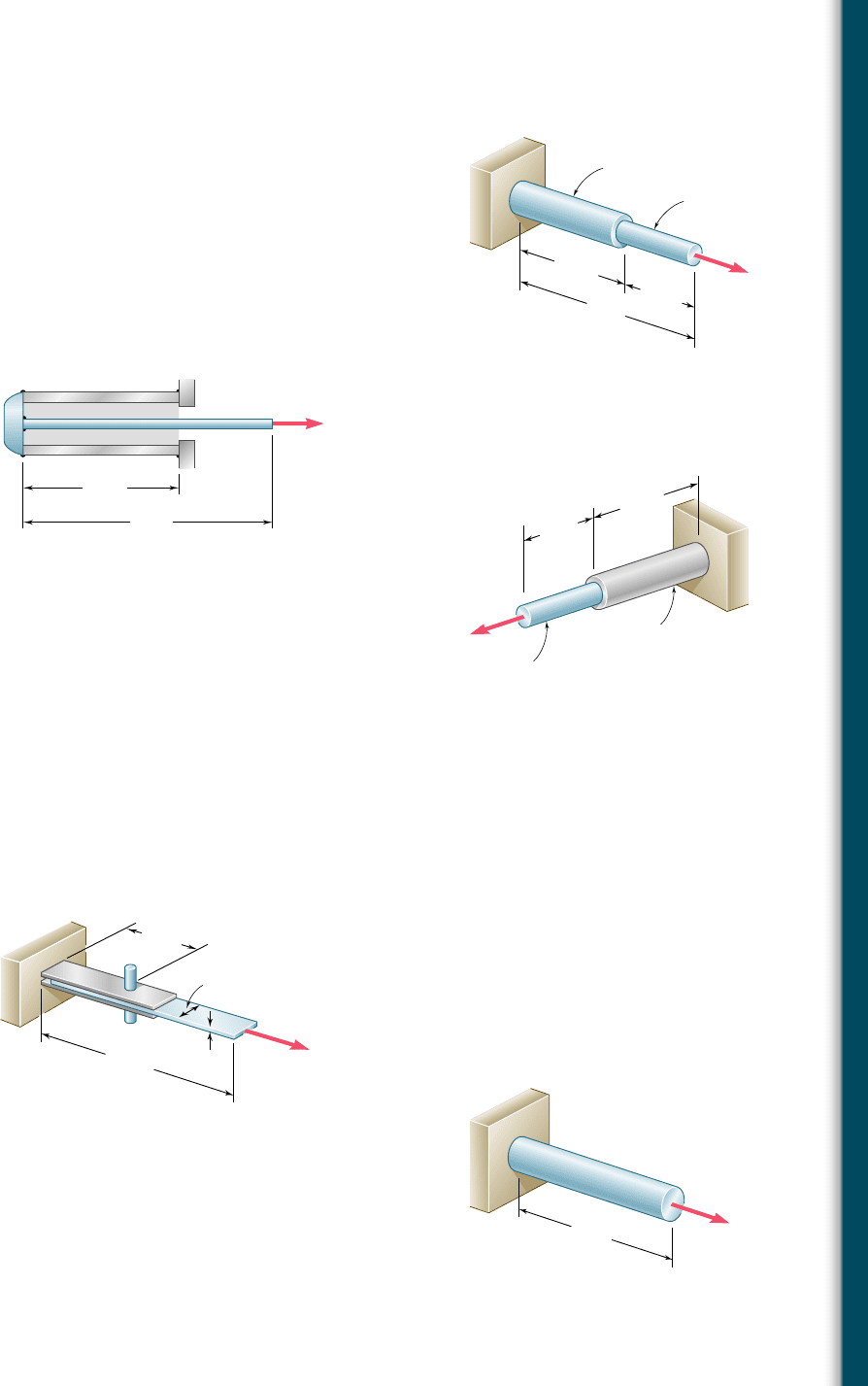
11.9 Using E 5 29 3 10
6
psi, determine (a) the strain energy of the
steel rod ABC when P 5 8 kips, (b) the corresponding strain
energy density in portions AB and BC of the rod.
bee80288_ch11_692-758.indd Page 710 11/12/10 5:13:45 PM user-f499bee80288_ch11_692-758.indd Page 710 11/12/10 5:13:45 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
711
Problems
11.10 Using E 5 200 GPa, determine (a) the strain energy of the steel
rod ABC when P 5 25 kN, (b) the corresponding strain-energy
density in portions AB and BC of the rod.
11.11 A 30-in. length of aluminum pipe of cross-sectional area 1.85 in
2
is welded to a fixed support A and to a rigid cap B. The steel rod
EF, of 0.75-in. diameter, is welded to cap B. Knowing that the
modulus of elasticity is 29 3 10
6
psi for the steel and 10.6 3 10
6
psi for the aluminum, determine (a) the total strain energy of the
system when P 5 8 kips, (b) the corresponding strain-energy den-
sity of the pipe CD and in the rod EF.
20-mm diameter
1.2 m
0.8 m
2 m
16-mm diamete
r
P
B
A
C
Fig. P11.10
11.12 Rod AB is made of a steel for which the yield strength is s
Y
5
450 MPa and E 5 200 GPa; rod BC is made of an aluminum alloy
for which s
Y
5 280 MPa and E 5 73 GPa. Determine the maxi-
mum strain energy that can be acquired by the composite rod ABC
without causing any permanent deformations.
11.13 A single 6-mm-diameter steel pin B is used to connect the steel
strip DE to two aluminum strips, each of 20-mm width and 5-mm
thickness. The modulus of elasticity is 200 GPa for the steel and
70 GPa for the aluminum. Knowing that for the pin at B the allow-
able shearing stress is t
all
5 85 MPa, determine, for the loading
shown, the maximum strain energy that can be acquired by the
assembled strips.
14-mm diameter
1.6 m
1.2 m
10-mm diameter
P
B
C
A
Fig. P11.12
1.25 m
0.5 m
5 mm
20 mm
B
A
D
C
E
P
Fig. P11.13
1.8 m
B
C
P
Fig. P11.14
11.14 Rod BC is made of a steel for which the yield strength is s
Y
5
300 MPa and the modulus of elasticity is E 5 200 GPa. Knowing
that a strain energy of 10 J must be acquired by the rod when
the axial load P is applied, determine the diameter of the rod
for which the factor of safety with respect to permanent defor-
mation is six.
Fig. P11.11
30 in.
D
B
A
EF
P
C
48 in.
bee80288_ch11_692-758.indd Page 711 11/12/10 5:13:53 PM user-f499bee80288_ch11_692-758.indd Page 711 11/12/10 5:13:53 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
712
Energy Methods
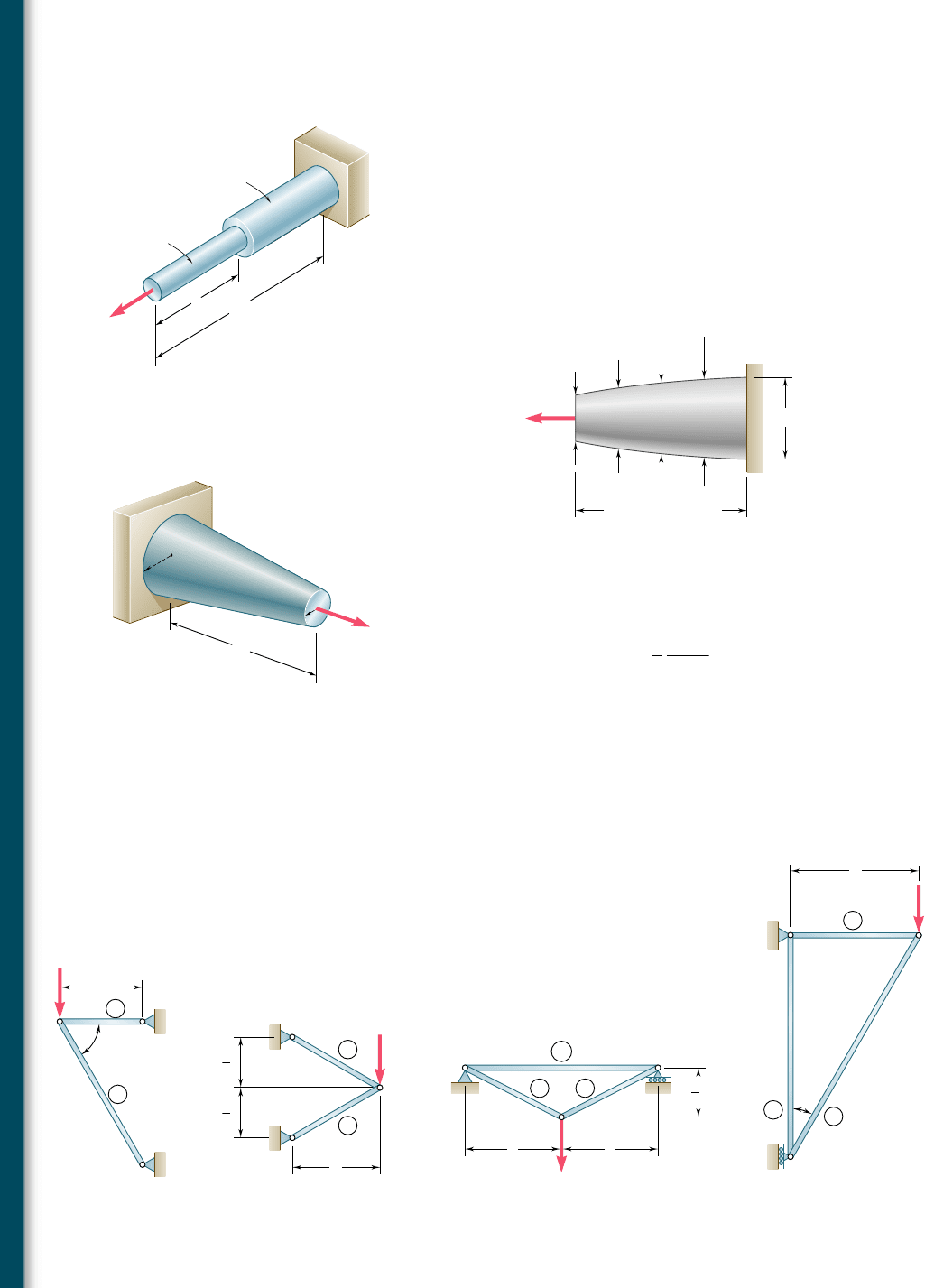
11.15 The assembly ABC is made of a steel for which E 5 200 GPa and
s
Y
5 320 MPa. Knowing that a strain energy of 5 J must be
acquired by the assembly as the axial load P is applied, determine
the factor of safety with respect to permanent deformation when
(a) x 5 300 mm, (b) x 5 600 mm.
11.16 Using E 5 10.6 3 10
6
psi, determine by approximate means the
maximum strain energy that can be acquired by the aluminum rod
shown if the allowable normal stress is s
all
5 22 ksi.
P
A
x
900 mm
18-mm diameter
12-mm diameter
B
C
Fig. P11.15
4 @ 1.5 in. 6 in.
A
B
1.5 in.
2.10 in.
2.55 in.
2.85 in.
3 in.
P
Fig. P11.16
11.17 Show by integration that the strain energy of the tapered rod AB is
U 5
1
4
P
2
L
EA
min
where A
min
is the cross-sectional area at end B.
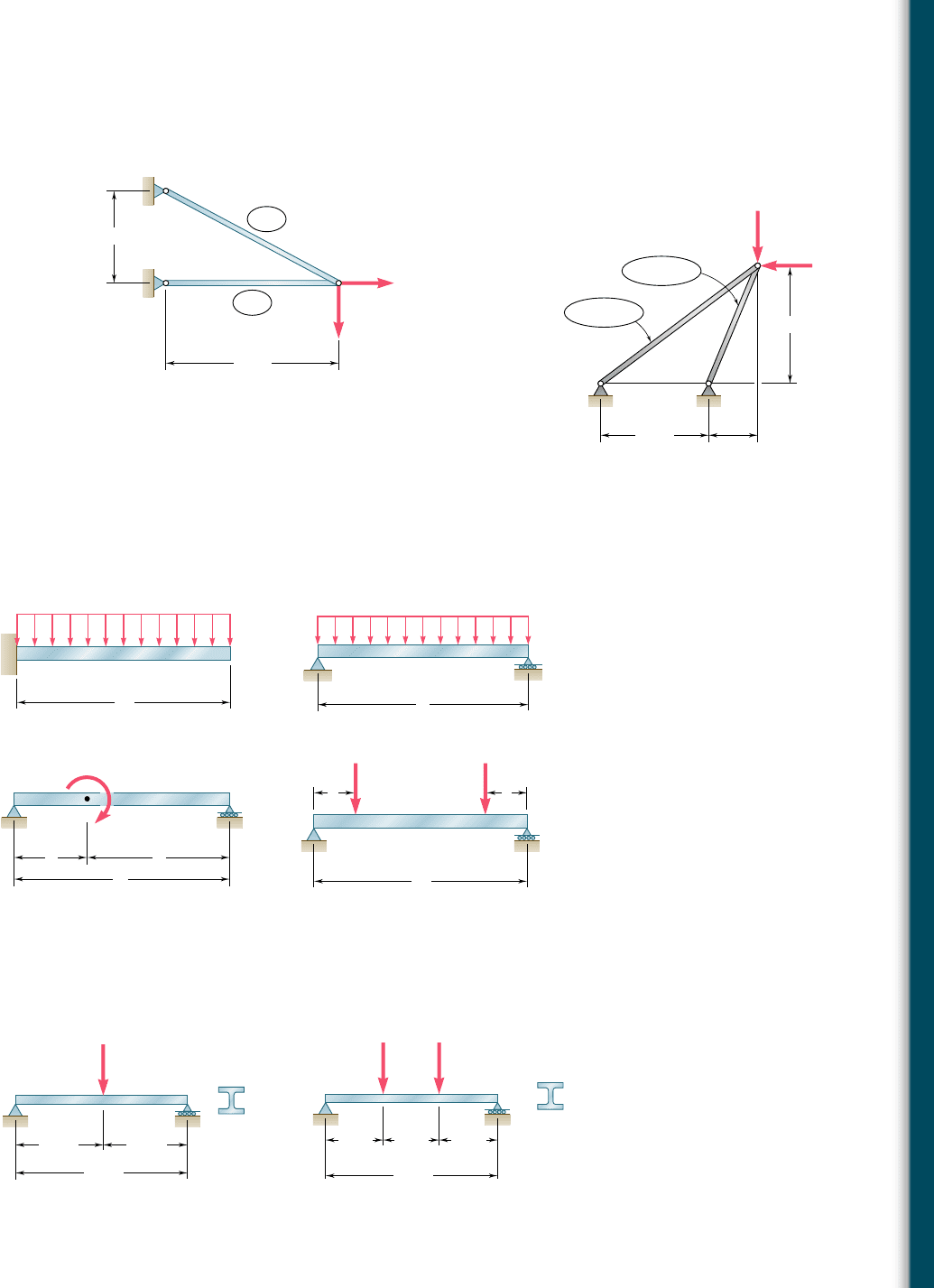
11.18 through 11.21 In the truss shown, all members are made of
the same material and have the uniform cross-sectional area indi-
cated. Determine the strain energy of the truss when the load P
is applied.
Fig. P11.17
L
B
2c
c
A
P
Fig. P11.18
l
C
A
A
P
D
B
60⬚
Fig. P11.20
A A
2A
DB
C
l l
P
l
1
2
Fig. P11.21
C
30°
B
l
A
A
A
D
P
l
l
D
B
C
1
2
l
1
2
A
A
P
Fig. P11.19
bee80288_ch11_692-758.indd Page 712 11/12/10 5:14:05 PM user-f499bee80288_ch11_692-758.indd Page 712 11/12/10 5:14:05 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
713
Problems
11.22 Each member of the truss shown is made of steel and has the
cross-sectional area shown. Using E 5 29 3 10
6
psi, determine the
strain energy of the truss for the loading shown.
3 in
2
4 in
2
20 kips
24 kips
D
B
C
7.5 ft
4 ft
Fig. P11.22
11.23 Each member of the truss shown is made of aluminum and has
the cross-sectional area shown. Using E 5 72 GPa, determine the
strain energy of the truss for the loading shown.
11.24 throug h 11.27 Taking into account only the effect of normal
stresses, determine the strain energy of the prismatic beam AB for
the loading shown.
30 kN
80 kN
2500 mm
2
2000 mm
2
C
D
B
2.2 m
1 m
2.4 m
Fig. P11.23
w
B
A
L
Fig. P11.24
B
w
A
L
Fig. P11.25
M
0
A
B
D
L
ab
Fig. P11.26
DE
B
A
aa
L
PP
Fig. P11.27
11.28 and 11.29 Using E 5 200 GPa, determine the strain energy
due to bending for the steel beam and loading shown. (Ignore the
effect of shearing stresses.)
Fig. P11.28
B
C
180 kN
A
2.4 m 2.4 m
4.8 m
W360 64
Fig. P11.29
B
DE
80 kN
A
80 kN
W310 74
1.6 m 1.6 m 1.6 m
4.8 m
bee80288_ch11_692-758.indd Page 713 11/12/10 5:14:22 PM user-f499bee80288_ch11_692-758.indd Page 713 11/12/10 5:14:22 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer
714
Energy Methods
11.30 and 11.31 Using E 5 29 3 10
6
psi, determine the strain energy
due to bending for the steel beam and loading shown. (Ignore the
effect of shearing stresses.)
C
B
4 kips
A
W6 9
8 ft
2 ft
Fig. P11.30
B
A
D
C
D
60 in.
15 in. 15 in.
1.5 in.
3 in.
2 kips
2 kips
Fig. P11.31
11.32 Assuming that the prismatic beam AB has a rectangular cross sec-
tion, show that for the given loading the maximum value of the
strain-energy density in the beam is
u
max
5 15
U
V
where U is the strain energy of the beam and V is its volume.
11.33 The ship at A has just started to drill for oil on the ocean floor at
a depth of 5000 ft. The steel drill pipe has an outer diameter of
8 in. and a uniform wall thickness of 0.5 in. Knowing that the top
of the drill pipe rotates through two complete revolutions before
the drill bit at B starts to operate and using G 5 11.2 3 10
6
psi,
determine the maximum strain energy acquired by the drill pipe.
11.34 Rod AC is made of aluminum and is subjected to a torque T applied
at C. Knowing that G 5 73 GPa and that portion BC of the rod is
hollow and has an inner diameter of 16 mm, determine the strain
energy of the rod for a maximum shearing stress of 120 MPa.
w
B
A
L
Fig. P11.32
5000 ft
A
B
Fig. P11.33
24-mm diameter
400 mm
500 mm
C
B
A
T
Fig. P11.34
11.35 Show by integration that the strain energy in the tapered rod AB
is
U 5
7
48
T
2
L
G
J
min
where J
min
is the polar moment of inertia of the rod at end B.
Fig. P11.35
L
B
2c
c
A
T
bee80288_ch11_692-758.indd Page 714 11/12/10 5:14:37 PM user-f499bee80288_ch11_692-758.indd Page 714 11/12/10 5:14:37 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
715
Problems
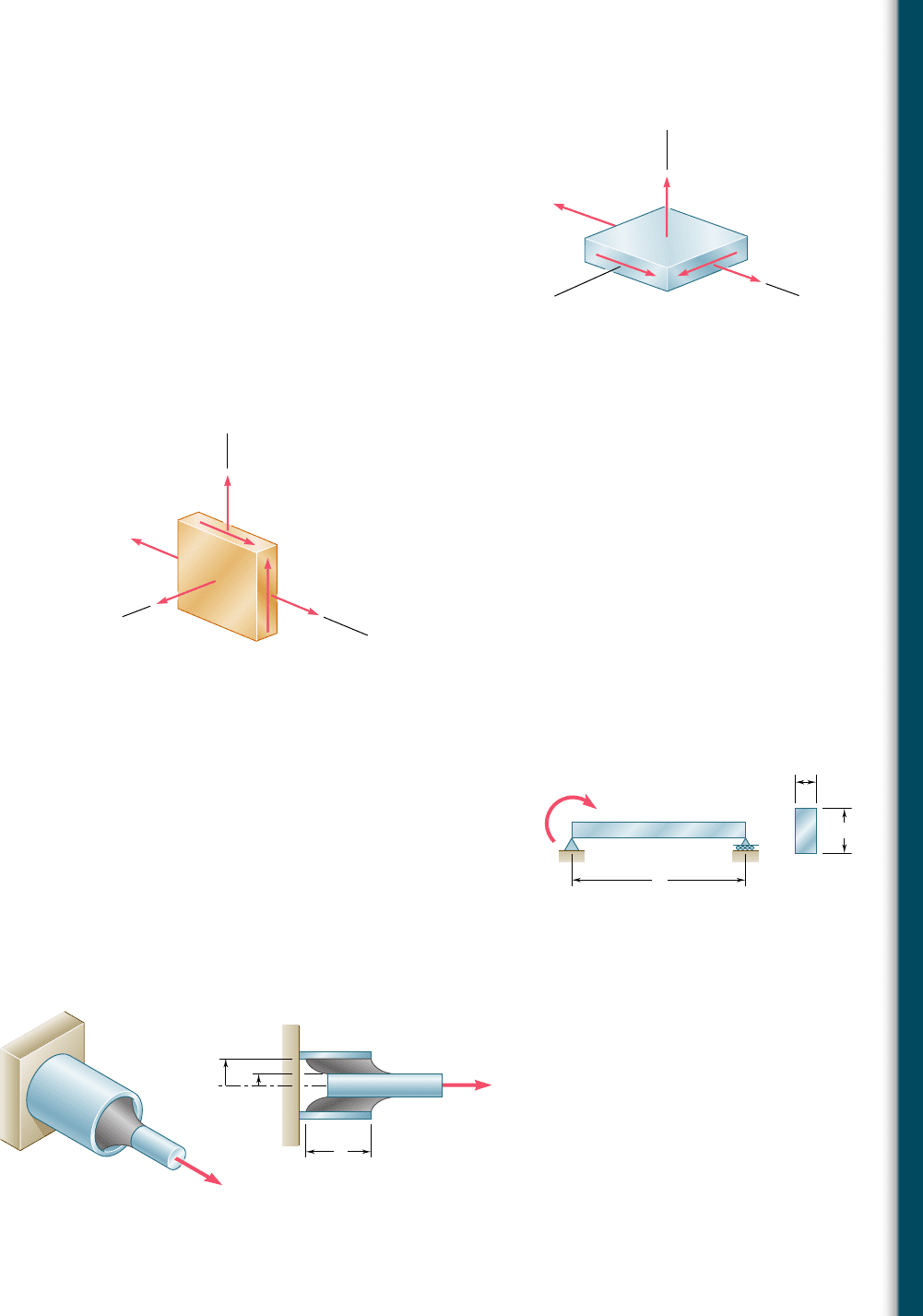
11.36 The state of stress shown occurs in a machine component made
of a grade of steel for which s
Y
5 65 ksi. Using the maximum-
distortion-energy criterion, determine the factor of safety associated
with the yield strength when (a) s
y
5 116 ksi, (b) s
y
5 216 ksi.
11.37 The state of stress shown occurs in a machine component made
of a grade of steel for which s
Y
5 65 ksi. Using the maximum-
distortion-energy criterion, determine the range of values of s
y
for
which the factor of safety associated with the yield strength is equal
to or larger than 2.2.
11.38 The state of stress shown occurs in a machine component made of
a brass for which s
Y
5 160 MPa. Using the maximum-distortion-
energy criterion, determine the range of values of s
z
for which
yield does not occur.
z
x
8 ksi
14 ksi
y
σ
y
Fig. P11.36 and P11.37
z
σ
z
75 MPa
y
x
100 MPa
20 MPa
Fig. P11.38 and P11.39
11.39 The state of stress shown occurs in a machine component made of
a brass for which s
Y
5 160 MPa. Using the maximum-distortion-
energy criterion, determine whether yield occurs when (a) s
z
5
145 MPa, (b) s
z
5 245 MPa.
11.4 0 Determine the strain energy of the prismatic beam AB, taking into
account the effect of both normal and shearing stresses.
*11.41 A vibration isolation support is made by bonding a rod A, of radius
R
1
, and a tube B, of inner radius R
2
, to a hollow rubber cylinder.
Denoting by G the modulus of rigidity of the rubber, determine
the strain energy of the hollow rubber cylinder for the loading
shown.
B
b
d
A
L
M
0
Fig. P11.40
Q
B
A
L
(b)
A
B
R
2
R
1
(a)
A
Q
Fig. P11.41
bee80288_ch11_692-758.indd Page 715 11/12/10 5:14:50 PM user-f499bee80288_ch11_692-758.indd Page 715 11/12/10 5:14:50 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer
716
Energy Methods
11.7 IMPACT LOADING
Consider a rod BD of uniform cross section which is hit at its end B
by a body of mass m moving with a velocity v
0
(Fig. 11.22a). As the
rod deforms under the impact (Fig. 11.22b), stresses develop within
the rod and reach a maximum value s
m
. After vibrating for a while,
the rod will come to rest, and all stresses will disappear. Such a
sequence of events is referred to as an impact loading (Photo 11.2).
In order to determine the maximum value s
m
of the stress
occurring at a given point of a structure subjected to an impact load-
ing, we are going to make several simplifying assumptions.
First, we assume that the kinetic energy T 5
1
2
mv
2
0
of the strik-
ing body is transferred entirely to the structure and, thus, that the
strain energy U
m
corresponding to the maximum deformation x
m
is
U
m
5
1
2
mv
2
0
(11.37)
This assumption leads to the following two specific requirements:
1. No energy should be dissipated during the impact.
2. The striking body should not bounce off the structure and
retain part of its energy. This, in turn, necessitates that the
inertia of the structure be negligible, compared to the inertia
of the striking body.
In practice, neither of these requirements is satisfied, and only
part of the kinetic energy of the striking body is actually transferred
to the structure. Thus, assuming that all of the kinetic energy of the
striking body is transferred to the structure leads to a conservative
design of that structure.
We further assume that the stress-strain diagram obtained from
a static test of the material is also valid under impact loading. Thus,
for an elastic deformation of the structure, we can express the maxi-
mum value of the strain energy as
U
m
5
#
s
2
m
2E
dV
(11.38)
In the case of the uniform rod of Fig. 11.22, the maximum
stress s
m
has the same value throughout the rod, and we write
U
m
5 s
2
m
Vy2E. Solving for s
m
and substituting for U
m
from Eq.
(11.37), we write
s
m
5
B
2U
m
E
V
5
B
mv
2
0
E
V
(11.39)
We note from the expression obtained that selecting a rod with a
large volume V and a low modulus of elasticity E will result in a
smaller value of the maximum stress s
m
for a given impact
loading.
In most problems, the distribution of stresses in the structure
is not uniform, and formula (11.39) does not apply. It is then
convenient to determine the static load P
m
, which would produce
the same strain energy as the impact loading, and compute from P
m
the corresponding value s
m
of the largest stress occurring in the
structure.
(a)
Area A
v
0
v 0
B
B
D
D
L
(b)
m
x
m
Fig. 11.22 Rod subject to impact loading.
Photo 11.2 Steam alternately lifts a weight
inside the pile driver and then propels it
downward. This delivers a large impact load to
the pile that is being driven into the ground.
bee80288_ch11_692-758.indd Page 716 11/12/10 5:15:00 PM user-f499bee80288_ch11_692-758.indd Page 716 11/12/10 5:15:00 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
