Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.


Apago PDF Enhancer
The deflection y
A
of the point A where the load P is applied is
obtained from Eq. (11.70). Since P is vertical and directed downward, y
A
represents a vertical deflection and is positive downward. We have
y
A
5
0U
0P
5
#
L
0
M
EI
0M
0P
dx
(11.73)
The bending moment M at a distance x from A is
M 52
1
Px 1
1
2
wx
2
2
(11.74)
and its derivative with respect to P is
0
M
0P
52x
Substituting for M and 0M
y
0P into Eq. (11.73), we write
y
A
5
1
EI
#
L
0
aPx
2
1
1
2
wx
3
b dx
y
A
5
1
EI
a
PL
3
3
1
wL
4
8
b
(11.75)
Substituting the given data, we have
y
A
5
1
5 3 10
6
N ? m
2
c
16 3 10
3
N212 m2
3
3
1
14 3 10
3
N/m212 m2
4
8
d
y
A
5 4.8 3 10
2
3
my
A
5 4.8 mmw
We note that the computation of the partial derivative 0M
y
0P could not
have been carried out if the numerical value of P had been substituted
for P in the expression (11.74) for the bending moment.
We can observe that the deflection x
j
of a structure at a given
point C
j
can be obtained by the direct application of Castigliano’s
theorem only if a load P
j
happens to be applied at C
j
in the direction
in which x
j
is to be determined. When no load is applied at C
j
, or
when a load is applied in a direction other than the desired one, we
can still obtain the deflection x
j
by Castigliano’s theorem if we use
the following procedure: We apply a fictitious or “dummy” load Q
j
at C
j
in the direction in which the deflection x
j
is to be determined
and use Castigliano’s theorem to obtain the deflection
x
j
5
0
U
0Q
j
(11.76)
due to Q
j
and the actual loads. Making Q
j
5 0 in Eq. (11.76) yields
the deflection at C
j
in the desired direction under the given
loading.
The slope u
j
of a beam at a point C
j
can be determined in a
similar manner by applying a fictitious couple M
j
at C
j
, computing
the partial derivative 0U
y
0M
j
, and making M
j
5 0 in the expression
obtained.
737
bee80288_ch11_692-758.indd Page 737 11/12/10 5:17:09 PM user-f499bee80288_ch11_692-758.indd Page 737 11/12/10 5:17:09 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
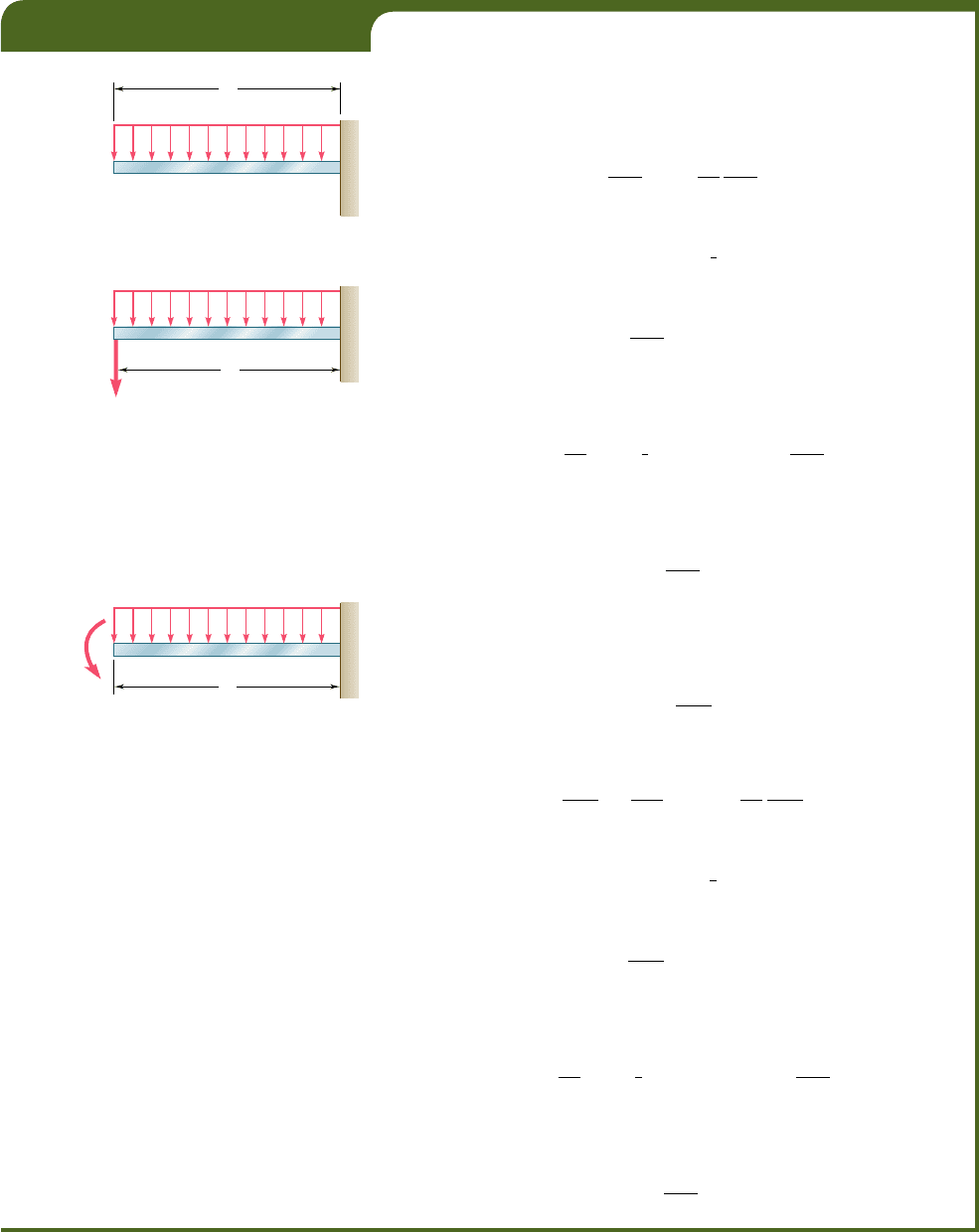
EXAMPLE 11.13
The cantilever beam AB supports a uniformly distributed load w (Fig.
11.41). Determine the deflection and slope at A.
Deflection at A. We apply a dummy downward load Q
A
at A
(Fig. 11.42) and write
y
A
5
0U
0Q
A
5
#
L
0
M
EI
0M
0Q
A
dx
(11.77)
The bending moment M at a distance x from A is
M 52Q
A
x 2
1
2
wx
2
(11.78)
and its derivative with respect to Q
A
is
0
M
0Q
A
52x
(11.79)
Substituting for M and 0M
/
0
Q
A
from (11.78) and (11.79) into (11.77), and
making Q
A
5 0, we obtain the deflection at A for the given loading:
y
A
5
1
EI
#
L
0
12
1
2
wx
2
212x2 dx 51
wL
4
8EI
Since the dummy load was directed downward, the positive sign indicates
that
y
A
5
wL
4
8EI
w
Slope at A. We apply a dummy counterclockwise couple M
A
at
A (Fig. 11.43) and write
u
A
5
0
U
0M
A
Recalling Eq. (11.17), we have
u
A
5
0
0M
A
#
L
0
M
2
2EI
dx 5
#
L
0
M
EI
0M
0M
A
dx
(11.80)
The bending moment M at a distance x from A is
M 52M
A
2
1
2
wx
2
(11.81)
and its derivative with respect to M
A
is
0
M
0M
A
521
(11.82)
Substituting for M and 0M
y
0M
A
from (11.81) and (11.82) into (11.80),
and making M
A
5 0, we obtain the slope at A for the given loading:
u
A
5
1
EI
#
L
0
12
1
2
wx
2
21212 dx 51
wL
3
6EI
Since the dummy couple was counterclockwise, the positive sign indicates
that the angle u
A
is also counterclockwise:
u
A
5
wL
3
6EI
a
B
A
w
L
Fig. 11.41
B
A
Q
A
w
L
Fig. 11.42
B
A
w
M
A
L
Fig. 11.43
738
bee80288_ch11_692-758.indd Page 738 11/12/10 5:17:10 PM user-f499bee80288_ch11_692-758.indd Page 738 11/12/10 5:17:10 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer
739
EXAMPLE 11.14
A load P is supported at B by two rods of the same material and of the
same cross-sectional area A (Fig. 11.44). Determine the horizontal and
vertical deflection of point B.
We apply a dummy horizontal load Q at B (Fig. 11.45). From
Castigliano’s theorem we have
x
B
5
0
U
0Q
y
B
5
0
U
0P
Recalling from Sec. 11.4 the expression (11.14) for the strain energy of a
rod, we write
U 5
F
2
BC
1BC2
2AE
1
F
2
BD
1BD2
2AE
where F
BC
and F
BD
represent the forces in BC and BD, respectively. We
have, therefore,
x
B
5
0U
0Q
5
F
BC
1
BC
2
AE
0F
BC
0Q
1
F
BD
1
BD
2
AE
0F
BD
0Q
(11.83)
and
y
B
5
0U
0P
5
F
BC
1
BC
2
AE
0F
BC
0P
1
F
BD
1
BD
2
AE
0F
BD
0P
(11.84)
From the free-body diagram of pin B (Fig. 11.46), we obtain
F
BC
5 0.6P 1 0.8Q F
BD
5 20.8P 1 0.6Q (11.85)
Differentiating these expressions with respect to Q and P, we write
0
F
BC
0Q
5 0.8
0
F
BD
0Q
5 0.6
0
F
BC
0P
5 0.6
0
F
BD
0P
520.8
(11.86)
Substituting from (11.85) and (11.86) into both (11.83) and (11.84), mak-
ing Q 5 0, and noting that BC 5 0.6l and BD 5 0.8l, we obtain the
horizontal and vertical deflections of point B under the given load P:
x
B
5
1
0.6P
2
1
0.6l
2
AE
10.821
1
20.8P
2
1
0.8l
2
AE
10.62
520.096
P
l
AE
y
B
5
1
0.6P
2
1
0.6l
2
AE
10.621
1
20.8P
2
1
0.8l
2
AE
120.82
5 10.728
P
l
AE
Referring to the directions of the loads Q and P, we conclude that
x
B
5 0.096
P
l
AE
z
y
B
5 0.728
P
l
AE
w
We check that the expression obtained for the vertical deflection of B is
the same that was found in Example 11.09.
C
D
B
l
P
3
3
4
4
Fig. 11.44
Q
C
D
B
l
P
3
3
4
4
Fig. 11.45
B
3
3
4
4
F
BC
F
BD
P
Q
Fig. 11.46
bee80288_ch11_692-758.indd Page 739 11/12/10 5:17:17 PM user-f499bee80288_ch11_692-758.indd Page 739 11/12/10 5:17:17 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
740
Energy Methods
*11.14 STATICALLY INDETERMINATE STRUCTURES
The reactions at the supports of a statically indeterminate elastic struc-
ture can be determined by Castigliano’s theorem. In the case of a
structure indeterminate to the first degree, for example, we designate
one of the reactions as redundant and eliminate or modify accordingly
the corresponding support. The redundant reaction is then treated as
an unknown load that, together with the other loads, must produce
deformations that are compatible with the original supports. We first
calculate the strain energy U of the structure due to the combined
action of the given loads and the redundant reaction. Observing that
the partial derivative of U with respect to the redundant reaction rep-
resents the deflection (or slope) at the support that has been elimi-
nated or modified, we then set this derivative equal to zero and solve
the equation obtained for the redundant reaction.† The remaining
reactions can be obtained from the equations of statics.
†This is in the case of a rigid support allowing no deflection. For other types of support,
the partial derivative of U should be set equal to the allowed deflection.
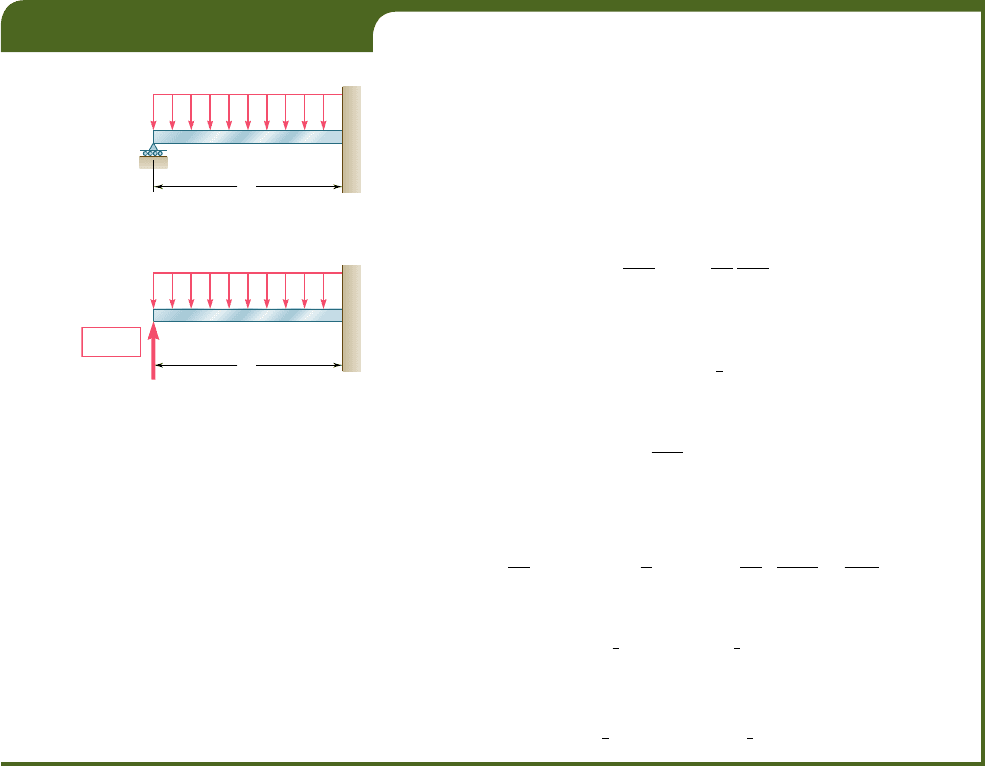
EXAMPLE 11.15
Determine the reactions at the supports for the prismatic beam and load-
ing shown (Fig. 11.47).
The beam is statically indeterminate to the first degree. We con-
sider the reaction at A as redundant and release the beam from that
support. The reaction R
A
is now considered as an unknown load (Fig.
11.48) and will be determined from the condition that the deflection y
A
at A must be zero. By Castigliano’s theorem y
A
5 0U
y
0R
A
, where U is the
strain energy of the beam under the distributed load and the redundant
reaction. Recalling Eq. (11.70), we write
y
A
5
0U
0R
A
5
#
L
0
M
EI
0M
0R
A
dx
(11.87)
We now express the bending moment M for the loading of Fig. 11.48.
The bending moment at a distance x from A is
M 5 R
A
x 2
1
2
wx
2
(11.88)
and its derivative with respect to R
A
is
0
M
0R
A
5 x
(11.89)
Substituting for M and 0M
/
0R
A
from (11.88) and (11.89) into
(11.87), we write
y
A
5
1
EI
#
L
0
aR
A
x
2
2
1
2
wx
3
b dx 5
1
EI
a
R
A
L
3
3
2
wL
4
8
b
Setting y
A
5 0 and solving for R
A
, we have
R
A
5
3
8
wL R
A
5
3
8
wLx
From the conditions of equilibrium for the beam, we find that the reac-
tion at B consists of the following force and couple:
R
B
5
5
8
wLx M
B
5
1
8
wL
2
i
B
A
w
L
Fig. 11.47
R
A
y
A
0
B
A
w
L
Fig. 11.48
bee80288_ch11_692-758.indd Page 740 11/12/10 5:17:26 PM user-f499bee80288_ch11_692-758.indd Page 740 11/12/10 5:17:26 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer
741
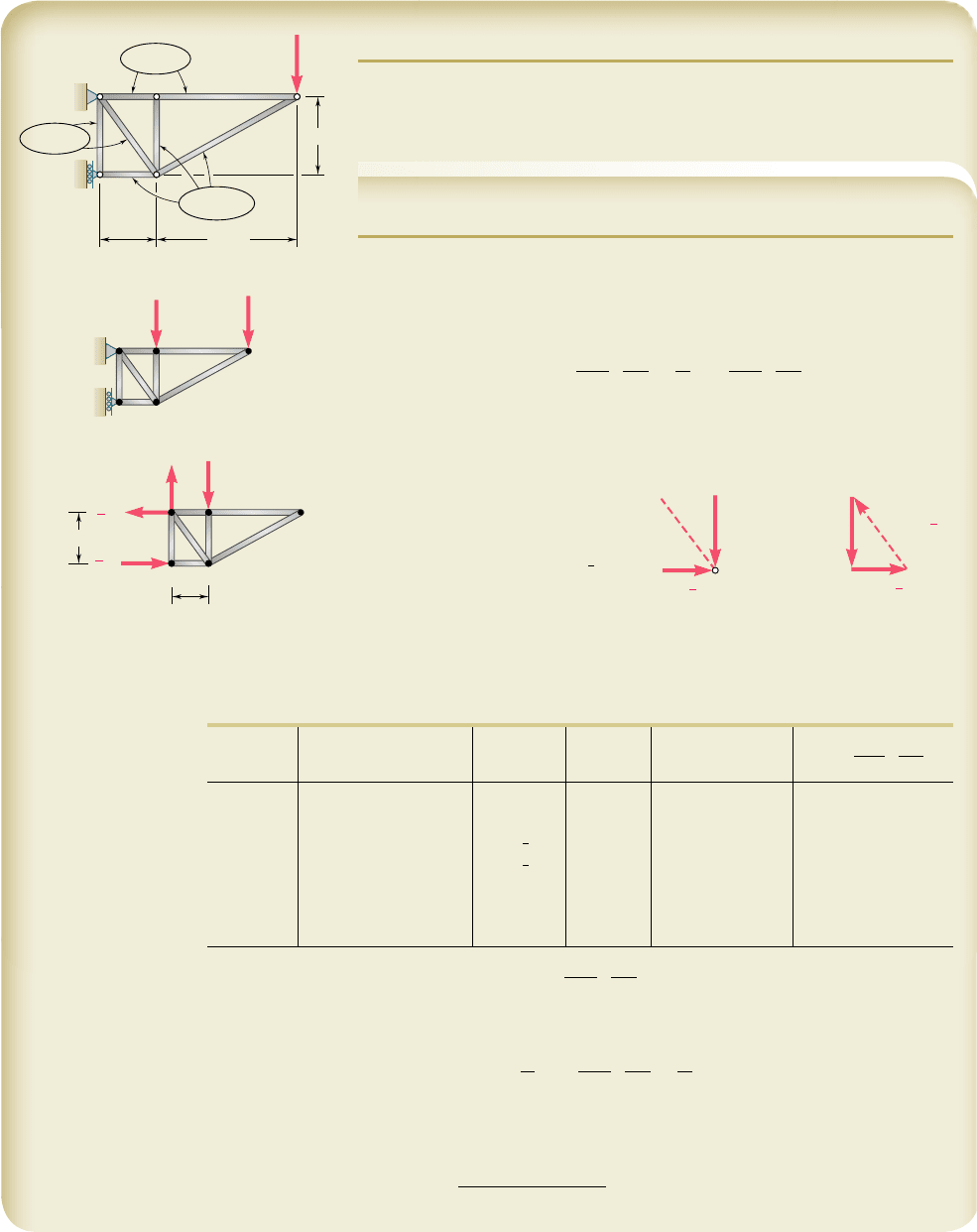
EXAMPLE 11.16
A load P is supported at B by three rods of the same material and the same
cross-sectional area A (Fig. 11.49). Determine the force in each rod.
Fig. 11.49
H
0.5l
0.6l
0.8l
C
D
l
P
B
H
C
D
P
B
R
H
y
H
0
Fig. 11.50
B
F
BC
F
BH
R
H
F
BD
P
Fig. 11.51
The structure is statically indeterminate to the first degree. We
consider the reaction at H as redundant and release rod BH from its sup-
port at H. The reaction R
H
is now considered as an unknown load (Fig.
11.50) and will be determined from the condition that the deflection y
H
of point H must be zero. By Castigliano’s theorem y
H
5 0U
y
0R
H
, where
U is the strain energy of the three-rod system under the load P and the
redundant reaction R
H
. Recalling Eq. (11.72), we write
y
H
5
F
BC
1
BC
2
AE
0F
BC
0R
H
1
F
BD
1
BD
2
AE
0F
BD
0R
H
1
F
BH
1
BH
2
AE
0F
BH
0R
H
(11.90)
We note that the force in rod BH is equal to R
H
and write
F
BH
5 R
H
(11.91)
Then, from the free-body diagram of pin B (Fig. 11.51), we obtain
F
BC
5 0.6P 2 0.6R
H
F
BD
5 0.8R
H
2 0.8P (11.92)
Differentiating with respect to R
H
the force in each rod, we write
0
F
BC
0R
H
520.6
0
F
BD
0R
H
5 0.8
0
F
BH
0R
H
5 1
(11.93)
Substituting from (11.91), (11.92), and (11.93) into (11.90), and not-
ing that the lengths BC, BD, and BH are, respectively, equal to 0.6l, 0.8l,
and 0.5l, we write
y
H
5
1
AE
310.6P 2 0.6R
H
210.6l2120.62
1
1
0.8R
H
2 0.8P
21
0.8l
21
0.8
2
1 R
H
1
0.5l
21
1
24
Setting y
H
5 0, we obtain
1.228R
H
2 0.728P 5 0
and, solving for R
H
,
R
H
5 0.593P
Carrying this value into Eqs. (11.91) and (11.92), we obtain the forces in
the three rods:
F
BC
5 10.244P F
BD
5 20.326P F
BH
5 10.593P
bee80288_ch11_692-758.indd Page 741 11/12/10 5:17:31 PM user-f499bee80288_ch11_692-758.indd Page 741 11/12/10 5:17:31 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
742
SOLUTION
Castigliano’s Theorem. Since no vertical load is applied at joint C,
we introduce the dummy load Q as shown. Using Castigliano’s theorem, and
denoting by F
i
the force in a given member i caused by the combined load-
ing of P and Q, we have, since E 5 constant,
y
C
5
a
a
F
i
L
i
A
i
E
b
0F
i
0Q
5
1
E
a
a
F
i
L
i
A
i
b
0F
i
0Q
(1)
Force in Members. Considering in sequence the equilibrium of joints
E, C, B, and D, we determine the force in each member caused by load Q.
Joint E: F
CE
5 F
DE
5 0
Joint C: F
AC
5 0; F
CD
5 2Q
Joint B: F
AB
5 0; F
BD
5 2
3
4
Q
The force in each member caused by the load P was previously found
in Sample Prob. 11.4. The total force in each member under the combined
action of Q and P is shown in the following table. Forming 0F
i
y
0Q for each
member, we then compute (F
i
L
i
yA
i
)
1
0F
i
y
0Q
2
as indicated in the table.
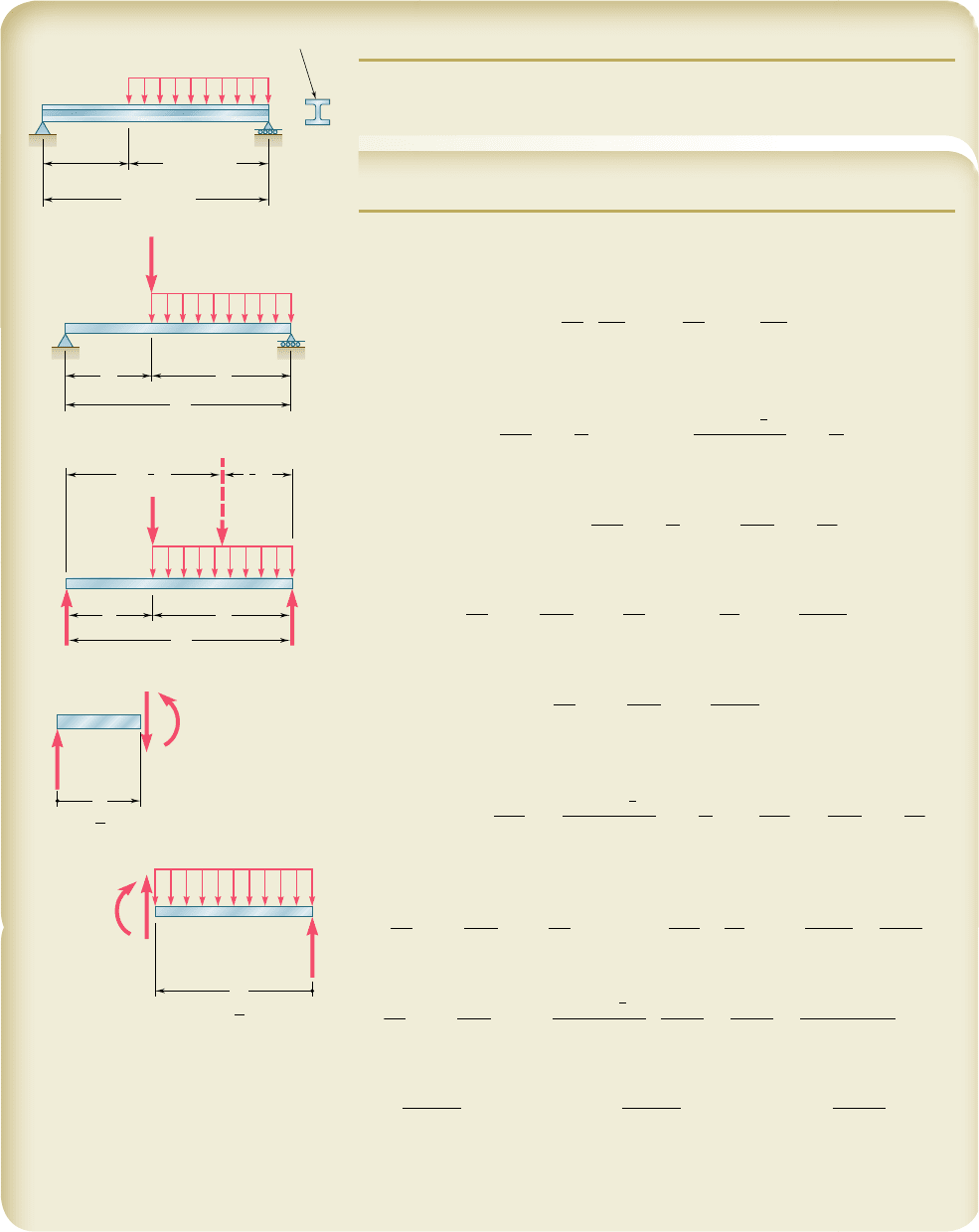
SAMPLE PROBLEM 11.5
For the truss and loading of Sample Prob. 11.4, determine the vertical
deflection of joint C.
a
a
F
i
L
i
A
i
b
0F
i
0Q
5 4306P 1 4263Q
Deflection of C. Substituting into Eq. (1), we have
y
C
5
1
E
a
a
F
i
L
i
A
i
b
0F
i
0Q
5
1
E
14306P 1 4263Q2
Since the load Q is not part of the original loading, we set Q 5 0. Substitut-
ing the given data, P 5 40 kN and E 5 73 GPa, we find
y
C
5
4306 140 3 10
3
N2
73
3
10
9
Pa
5 2.36 3 10
23
m
y
C
5 2.36 mmw
◀
Member F
i
0F
i
y0Q L
i
, m A
i
, m
2
a
F
i
L
i
A
i
b
0F
i
0
Q
AB 0 0 0.8 500 3 10
26
0
AC 115Py8 0 0.6 500 3 10
26
0
AD 15Py4 1 5Qy4
5
4
1.0 500 3 10
26
13125P 1 3125Q
BD 221Py8 2 3Qy4 2
3
4
0.6 1000 3 10
26
11181P 1 338Q
CD 2Q 21 0.8 1000 3 10
26
1 800Q
CE 115Py8 0 1.5 500 3 10
26
0
DE 217Py8 0 1.7 1000 3 10
26
0
500 mm
2
0.8 m
0.6 m
1.5 m
P 40 kN
A
C
E
B
D
500 mm
2
1000 mm
2
C
Q
A
BD
E
P
A
C
QQ
0.8 m
Q
Q
3
4
3
4
E
B
0.6 m
D
Joint D Force triangle
D
F
AD
F
CD
Q
F
CD
Q
3
4
F
BD
Q
3
4
F
BD
Q
5
4
F
AD
Q
bee80288_ch11_692-758.indd Page 742 11/12/10 5:17:39 PM user-f499bee80288_ch11_692-758.indd Page 742 11/12/10 5:17:39 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
743
SOLUTION
Castigliano’s Theorem. Since the given loading does not include a
vertical load at point D, we introduce the dummy load Q as shown. Using
Castigliano’s theorem and noting that EI is constant, we write
y
D
5
#
M
EI
a
0M
0Q
b
dx 5
1
EI
#
M
a
0M
0Q
b
dx
(1)
The integration will be performed separately for portions AD and DB.
Reactions. Using the free-body diagram of the entire beam, we find
R
A
5
wb
2
2L
1 Q
b
L
x
R
B
5
wb1a 1
1
2
b2
L
1 Q
a
L
x
Portion AD of Beam. Using the free body shown, we find
M
1
5 R
A
x 5
a
wb
2
2L
1 Q
b
L
b
x
0M
1
0Q
51
b
x
L
Substituting into Eq. (1) and integrating from A to D gives
1
EI
#
M
1
0M
1
0Q
dx 5
1
EI
#
a
0
R
A
x a
bx
L
b dx 5
R
A
a
3
b
3EIL
We substitute for R
A
and then set the dummy load Q equal to zero.
1
EI
#
M
1
0M
1
0Q
dx 5
wa
3
b
3
6EIL
2
(2)
Portion DB of Beam. Using the free body shown, we find that the
bending moment at a distance v from end B is
M
2
5 R
B
v 2
wv
2
2
5
c
wb1a 1
1
2
b2
L
1 Q
a
L
d
v 2
wv
2
2
0
M
2
0Q
51
av
L
Substituting into Eq. (1) and integrating from point B where v 5 0, to point
D where v 5 b, we write
1
EI
#
M
2
0M
2
0Q
dv 5
1
EI
#
b
0
aR
B
v 2
wv
2
2
b a
av
L
b dv 5
R
B
ab
3
3EIL
2
wab
4
8EIL
Substituting for R
B
and setting Q 5 0,
1
EI
#
M
2
0M
2
0Q
dv 5 c
wb1a 1
1
2
b2
L
d
ab
3
3EIL
2
wab
4
8EIL
5
5a
2
b
4
1 ab
5
24EIL
2
w
(3)
Deflection at Point D. Recalling Eqs. (1), (2), and (3), we have
y
D
5
wab
3
24EIL
2
14a
2
1 5ab 1 b
2
25
wab
3
24EIL
2
14a 1 b21a 1 b25
wab
3
24EIL
14a 1 b2
From Appendix C we find that I 5 68.9 in
4
for a W10 3 15. Substituting
for I, w, a, b, and L their numerical values, we obtain
y
D
5 0.262 in.w
◀
SAMPLE PROBLEM 11.6
For the beam and loading shown, determine the deflection at point D. Use
E 5 29 3 10
6
psi.
B
A
D
L 12 ft
a 4.5 ft
w 1.8 kips/ft
b 7.5 ft
W10 15
B
A
D
L
a
w
b
Q
B
A
D
L
a
a b
1
2
wb
b
R
A
R
B
b
1
2
Q
x
(x
a)
A
From A to D
M
1
R
A
V
1
w
From B to D
B
v
R
B
M
2
V
2
(v
b)
bee80288_ch11_692-758.indd Page 743 11/12/10 5:17:49 PM user-f499bee80288_ch11_692-758.indd Page 743 11/12/10 5:17:49 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
744
SOLUTION
Castigliano’s Theorem. The beam is indeterminate to the first degree
and we choose the reaction R
A
as redundant. Using Castigliano’s theorem,
we determine the deflection at A due to the combined action of R
A
and the
distributed load. Since EI is constant, we write
y
A
5
#
M
EI
a
0M
0R
A
b
dx 5
1
EI
#
M
0M
0R
A
dx
(1)
The integration will be performed separately for portions AB and BC of the
beam. Finally, R
A
is obtained by setting y
A
equal to zero.
Free Body: Entire Beam. We express the reactions at B and C in
terms of R
A
and the distributed load
R
B
5
9
4
wL 2 3R
A
R
C
5 2R
A
2
3
4
wL (2)
Portion AB of Beam. Using the free-body diagram shown, we find
M
1
5 R
A
x 2
wx
2
2
0
M
1
0R
A
5 x
Substituting into Eq. (1) and integrating from A to B, we have
1
EI
#
M
1
0M
0R
A
dx 5
1
EI
#
L
0
aR
A
x
2
2
wx
3
2
b dx 5
1
EI
a
R
A
L
3
3
2
wL
4
8
b
(3)
Portion BC of Beam. We have
M
2
5
a
2R
A
2
3
4
wL
b
v 2
wv
2
2
0
M
2
0R
A
5 2v
Substituting into Eq. (1) and integrating from C, where v 5 0, to B, where
v 5
1
2
L, we have
1
EI
#
M
2
0M
2
0R
A
dv 5
1
EI
#
L
y
2
0
a4R
A
v
2
2
3
2
wLv
2
2 wv
3
b dv
5
1
EI
a
R
A
L
3
6
2
wL
4
16
2
wL
4
64
b
5
1
EI
a
R
A
L
3
6
2
5wL
4
64
b
(4)
Reaction at A. Adding the expressions obtained in (3) and (4), we
determine y
A
and set it equal to zero
y
A
5
1
EI
a
R
A
L
3
3
2
wL
4
8
b
1
1
EI
a
R
A
L
3
6
2
5wL
4
64
b
5 0
Solving for R
A
,
R
A
5
13
3
2
wL
R
A
5
13
3
2
wLx
◀
Reactions at B and C. Substituting for R
A
into Eqs. (2), we obtain
R
B
5
33
3
2
wLx
R
C
5
w
L
16
x
◀
SAMPLE PROBLEM 11.7
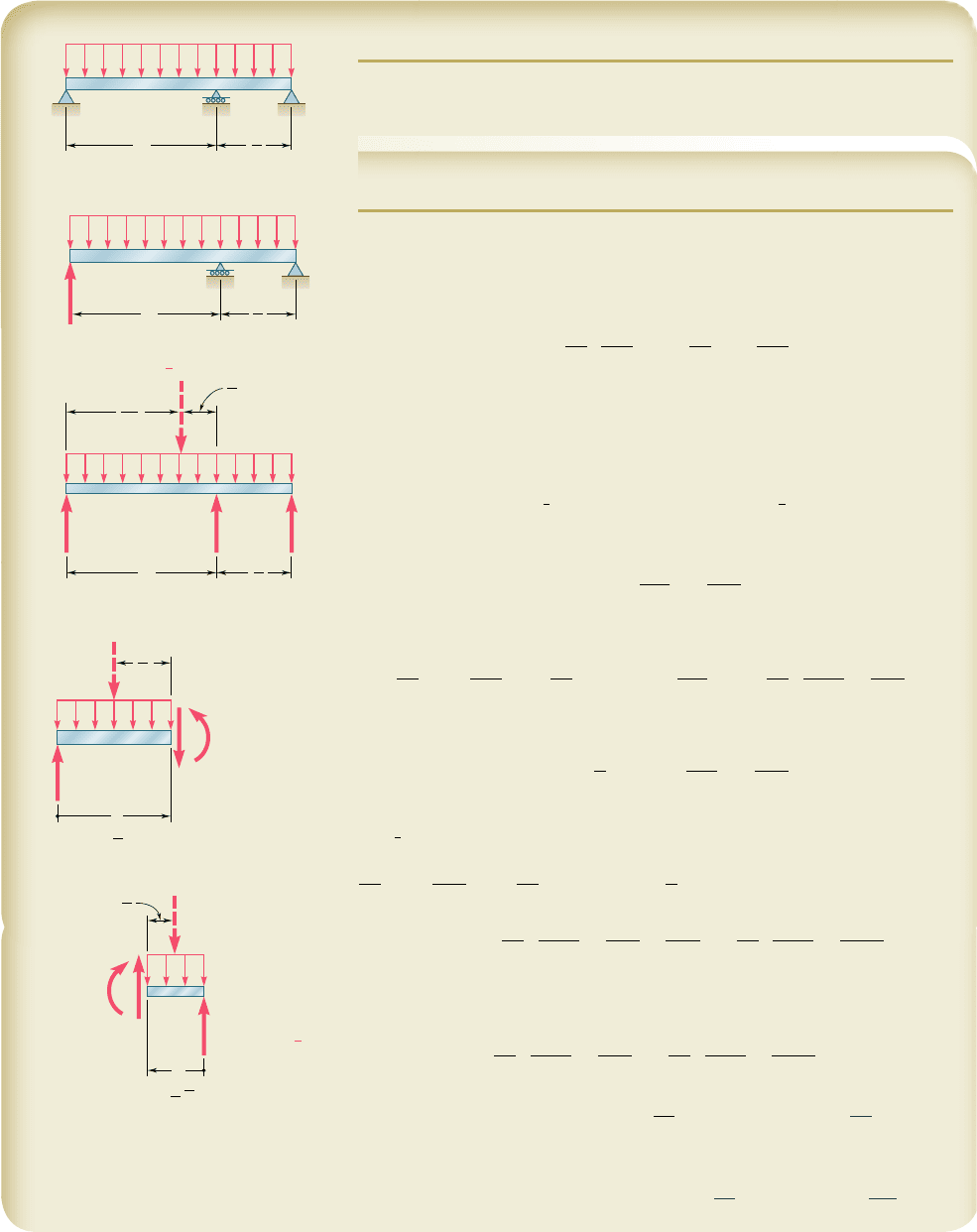
For the uniform beam and loading shown, determine the reactions at the
supports.
C
A
B
L
L
2
w
B
A
C
L
R
A
L
2
w
B
A
C
L
wL
3
2
L
4
3L
4
L
2
R
A
R
B
R
C
wx
x
A
From A to B
M
1
R
A
V
1
x
2
(x
L)
(v
)
From C to B
C
v
R
C
2R
A
M
2
V
2
L
2
v
2
wv
wL
3
4
bee80288_ch11_692-758.indd Page 744 11/19/10 11:34:35 PM user-f499bee80288_ch11_692-758.indd Page 744 11/19/10 11:34:35 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
PROBLEMS
745
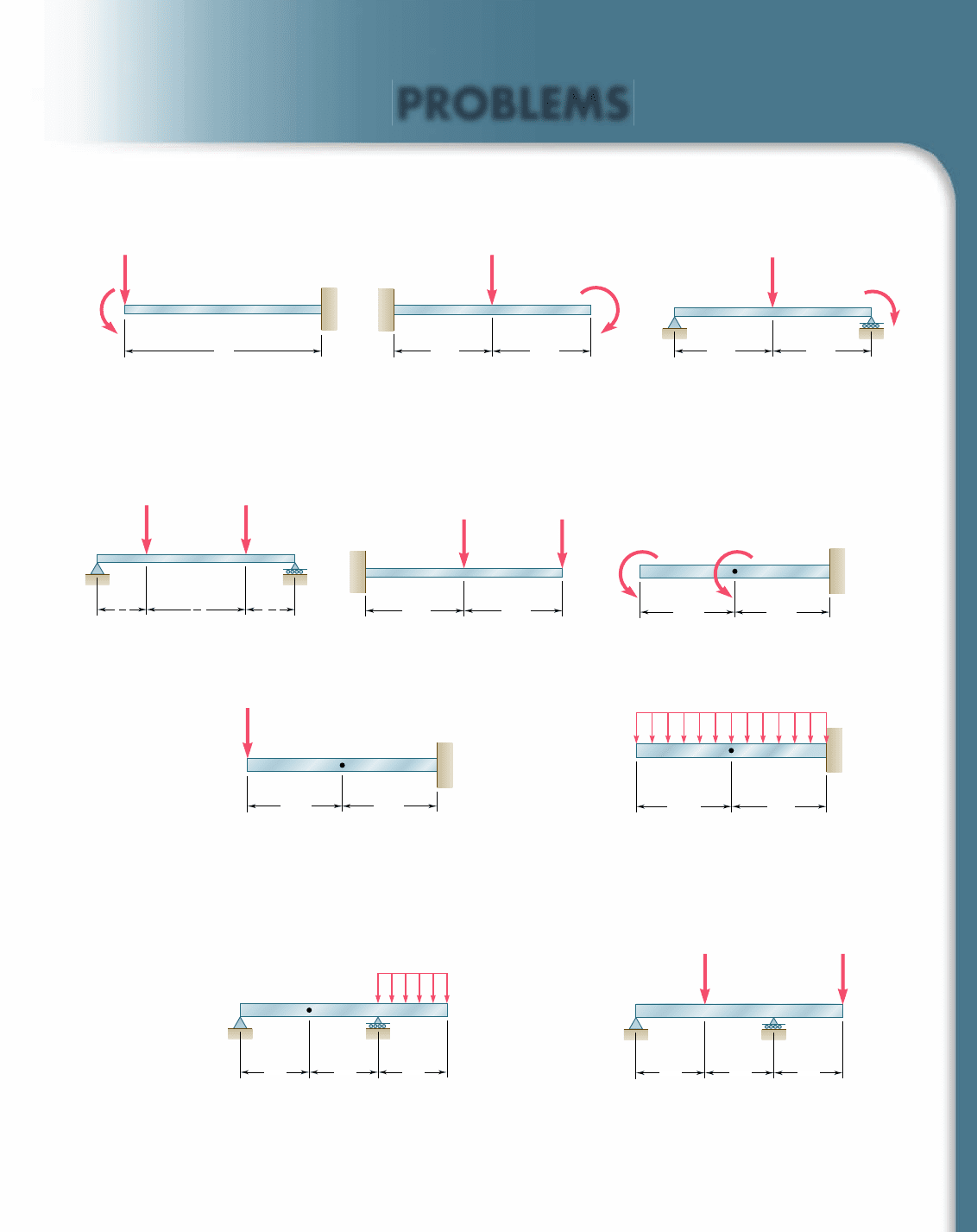
11.77 throu g h 11.79 Using the information in Appendix D, com-
pute the work of the loads as they are applied to the beam (a) if
the load P is applied first, (b) if the couple M is applied first.
L
B
A
M
0
P
Fig. P11.77
B
A
C
M
0
L/2 L/2
P
Fig. P11.78
B
A
C
P
M
0
L/2 L/2
Fig. P11.79
11.80 thr ough 11.82 For the beam and loading shown, (a) compute
the work of the loads as they are applied successively to the beam,
using the information provided in Appendix D, (b) compute the
strain energy of the beam by the method of Sec. 11.4 and show
that it is equal to the work obtained in part a.
D
E
B
A
L
4
L
2
L
4
P P
Fig. P11.80
B
A
C
L/2 L/2
P
P
Fig. P11.81
C
B
L/2 L/2
A
M
0
M
0
Fig. P11.82
11.83 and 11.84 For the prismatic beam shown, determine the
deflection of point D.
B
D
L/2 L/2
A
P
Fig. P11.83 and P11.85
11.85 and 11.86 For the prismatic beam shown, determine the slope
at point D.
11.87 and 11.88 For the prismatic beam shown, determine the
deflection at point D.
L/2 L/2
B
A
D
w
Fig. P11.84 and P11.86
11.89 and 11.90 For the prismatic beam shown, determine the slope
at point D.
A
B
w
DE
L/2 L/2
L/2
Fig. P11.87 and P11.89
A
B
DE
L/2 L/2
L/2
P P
Fig. P11.88 and P11.90
bee80288_ch11_692-758.indd Page 745 11/12/10 5:18:16 PM user-f499bee80288_ch11_692-758.indd Page 745 11/12/10 5:18:16 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
Apago PDF Enhancer
746
Energy Methods
11.91 For the beam and loading shown, determine the slope at end A.
Use E 5 200 GPa.
11.92 For the beam and loading shown, determine the slope at end C.
Use E 5 29 3 10
6
psi.
B
C
160 kN
A
2.4 m 2.4 m
4.8 m
W310 74
Fig. P11.91
B
A
C
6 ft
2 ft
8 kips 4 kips
W14 30
Fig. P11.92 and P11.93
11.93 For the beam and loading shown, determine the deflection at end C.
Use E 5 29 3 10
6
psi.
11.94 For the beam and loading shown, determine the deflection at
point D. Use E 5 200 GPa.
B
A
DE
0.6 m
90 kN 90 kN
0.6 m
2 m
S250 37.8
Fig. P11.94
11.95 and 11.96 For the beam and loading shown, determine the
deflection at point B. Use E 5 200 GPa.
A
CB
0.6 m 0.9 m
40 mm
80 mm
5 kN/m
4 kN
Fig. P11.95
8 kN
A
C
18 kN/m
B
1 m 1.5 m
2.5 m
W250 22.3
Fig. P11.96
11.97 For the beam and loading shown, determine the deflection at point C.
Use E 5 29 3 10
6
psi.
B
D
C
A
8 kips
S8 18.4
6 ft
3 ft
3 ft
Fig. P11.97 and P11.98
11.98 For the beam and loading shown, determine the slope at end A.
Use E 5 29 3 10
6
psi.
bee80288_ch11_692-758.indd Page 746 11/15/10 8:06:16 PM user-f499bee80288_ch11_692-758.indd Page 746 11/15/10 8:06:16 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11
