Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

757

COMPUTER PROBLEMS

The following problems are designed to be solved with a computer.

11.C1 A rod consisting of n elements, each of which is homogeneous and

of uniform cross section, is subjected to a load P applied at its free end.

The length of element i is denoted by L

and its diameter by d

. (a) Denot-

ing by E the modulus of elasticity of the material used in the rod, write a

computer program that can be used to determine the strain energy acquired

by the rod and the deformation measured at its free end. (b) Use this pro-

gram to determine the strain energy and deformation for the rods of Probs.

11.9 and 11.10.

11.C2 Two 0.75 3 6-in. cover plates are welded to a W8 3 18 rolled-steel

beam as shown. The 1500-lb block is to be dropped from a height h 5 2 in.

onto the beam. (a) Write a computer program to calculate the maximum

normal stress on transverse sections just to the left of D and at the center

of the beam for values of a from 0 to 60 in. using 5-in. increments. (b) From

the values considered in part a, select the distance a for which the maximum

normal stress is as small as possible. Use E 5 29 3 10

psi.

Element i

Element 1

Element n

Fig. P11.C1

60 in. 60 in.

1500 lb

 6 in.

W8  18

Fig. P11.C2

11.C3 The 16-kg block D is dropped from a height h onto the free end

of the steel bar AB. For the steel used s

all

5 120 MPa and E 5 200 GPa.

(a) Write a computer program to calculate the maximum allowable height

h for values of the length L from 100 mm to 1.2 m, using 100-mm incre-

ments. (b) From the values considered in part a, select the length corre-

sponding to the largest allowable height.

24 mm

Fig. P11.C3

bee80288_ch11_692-758.indd Page 757 11/12/10 5:21:20 PM user-f499bee80288_ch11_692-758.indd Page 757 11/12/10 5:21:20 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer

758

Energy Methods

11.C4 The block D of mass m 5 8 kg is dropped from a height h 5 750 mm

onto the rolled-steel beam AB. Knowing that E 5 200 GPa, write a com-

puter program to calculate the maximum deflection of point E and the

maximum normal stress in the beam for values of a from 100 to 900 m,

using 100-mm increments.

1.8 m

W150  13.5

Fig. P11.C4

11.C5 The steel rods AB and BC are made of a steel for which s

300 MPa and E 5 200 GPa. (a) Write a computer program to calculate for

values of a from 0 to 6 m, using 1-m increments, the maximum strain energy

that can be acquired by the assembly without causing any permanent defor-

mation. (b) For each value of a considered, calculate the diameter of a

uniform rod of length 6 m and of the same mass as the original assembly,

and the maximum strain energy that could be acquired by this uniform rod

without causing permanent deformation.

10-mm diameter

6 m

6-mm diameter

Fig. P11.C5

11.C6 A 160-lb diver jumps from a height of 20 in. onto end C of a diving

board having the uniform cross section shown. Write a computer program

to calculate for values of a from 10 to 50 in., using 10-in. increments, (a) the

maximum deflection of point C, (b) the maximum bending moment in the

board, (c) the equivalent static load. Assume that the diver’s legs remain

rigid and use E 5 1.8 3 10

psi.

12 ft

16 in.

2.65 in.

20 in.

Fig. P11.C6

bee80288_ch11_692-758.indd Page 758 11/12/10 5:21:27 PM user-f499bee80288_ch11_692-758.indd Page 758 11/12/10 5:21:27 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer

APPENDIX A Moments of Areas A2

APPENDIX B Typical Properties of Selected

Materials Used in Engineering A12

APPENDIX C Properties of Rolled-Steel Shapes† A16

APPENDIX D Beam Deflections and Slopes A28

APPENDIX E Fundamentals of Engineering

Examination A29

†Courtesy of the American Institute of Steel Construction, Chicago, Illinois.

Appendices

bee80288_app_A1-A30.indd Page A1 11/19/10 6:02:13 PM user-f499bee80288_app_A1-A30.indd Page A1 11/19/10 6:02:13 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app

Apago PDF Enhancer

Moments of Areas

A.1 FIRST MOMENT OF AN AREA;

CENTROID OF AN AREA

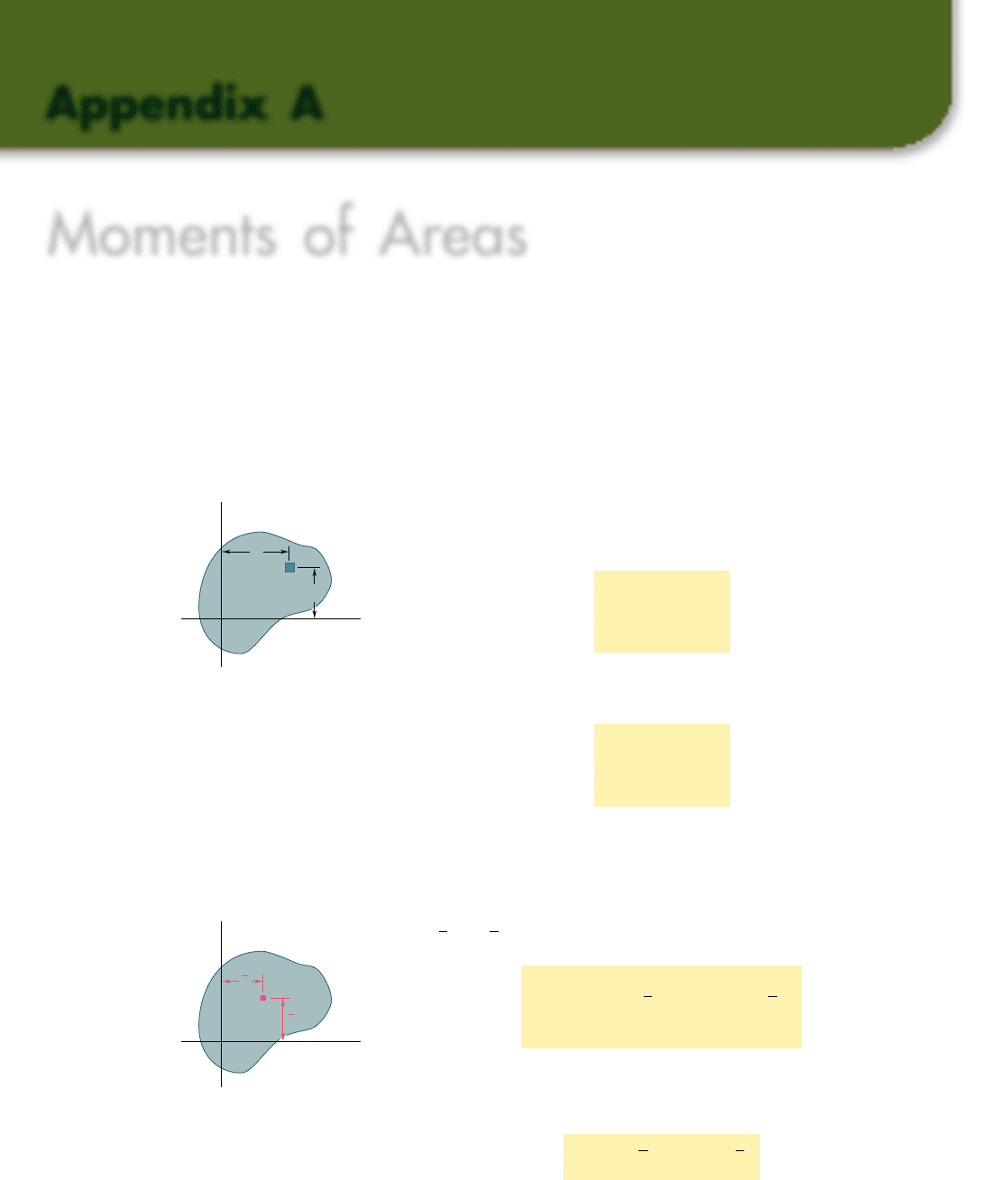
Consider an area A located in the xy plane (Fig. A.1). Denoting by

x and y the coordinates of an element of area dA, we define the first

moment of the area A with respect to the x axis as the integral

y dA

(A.1)

Similarly, the first moment of the area A with respect to the y axis is

defined as the integral

x dA

(A.2)

We note that each of these integrals may be positive, negative, or

zero, depending on the position of the coordinate axes. If SI units

are used, the first moments

and

are expressed in

;

if U.S. customary units are used, they are expressed in f

or i

The centroid of the area A is defined as the point C of coordi-

nates

and y (Fig. A.2), which satisfy the relations

x dA 5 Ax

y dA 5 Ay

(A.3)

Comparing Eqs. (A.1) and (A.2) with Eqs. (A.3), we note that the

first moments of the area A can be expressed as the products of the

area and of the coordinates of its centroid:

5 AyQ

5 Ax (A.4)

Fig. A.1

Fig. A.2

Appendix A

bee80288_app_A1-A30.indd Page A2 11/19/10 6:02:13 PM user-f499bee80288_app_A1-A30.indd Page A2 11/19/10 6:02:13 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app

Apago PDF Enhancer

When an area possesses an axis of symmetry, the first moment

of the area with respect to that axis is zero. Indeed, considering the

area A of Fig. A.3, which is symmetric with respect to the y axis, we

observe that to every element of area dA of abscissa x corresponds

an element of area

¿ of abscissa 2

It follows that the integral in

Eq. (A.2) is zero and, thus, that Q

5 0. It also follows from the first

of the relations (A.3) that

Thus, if an area A possesses an axis

of symmetry, its centroid C is located on that axis.

A.1 First Moment of an Area

Since a rectangle possesses two axes of symmetry (Fig. A.4a),

the centroid C of a rectangular area coincides with its geometric

center. Similarly, the centroid of a circular area coincides with the

center of the circle (Fig. A.4b).

When an area possesses a center of symmetry O, the first

moment of the area about any axis through O is zero. Indeed, con-

sidering the area A of Fig. A.5, we observe that to every element of

area dA of coordinates x and y corresponds an element of area

of coordinates 2

and 2y. It follows that the integrals in Eqs. (A.1)

and (A.2) are both zero, and that Q

5 Q

5 0. It also follows from

Eqs. (A.3) that

x 5 y 5 0, that is, the centroid of the area coincides

with its center of symmetry.

When the centroid C of an area can be located by symmetry,

the first moment of that area with respect to any given axis can be

readily obtained from Eqs. (A.4). For example, in the case of the

rectangular area of Fig. A.6, we have

5 Ay 5 1bh21

h25

and

5 Ax 5 1bh21

b25

In most cases, however, it is necessary to perform the integrations

indicated in Eqs. (A.1) through (A.3) to determine the first moments

and the centroid of a given area. While each of the integrals involved

is actually a double integral, it is possible in many applications to

select elements of area dA in the shape of thin horizontal or vertical

strips, and thus to reduce the computations to integrations in a single

variable. This is illustrated in Example A.01. Centroids of common

geometric shapes are indicated in a table inside the back cover of

this book.

dA'

–x

Fig. A.3

(a)(b)

Fig. A.4

Fig. A.6

y 

x 

dA'

–y

–x

Fig. A.5

bee80288_app_A1-A30.indd Page A3 11/19/10 6:02:19 PM user-f499bee80288_app_A1-A30.indd Page A3 11/19/10 6:02:19 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app

Apago PDF Enhancer

A.2 DETERMINATION OF THE FIRST MOMENT AND

CENTROID OF A COMPOSITE AREA

Consider an area A, such as the trapezoidal area shown in Fig. A.9,

which may be divided into simple geometric shapes. As we saw in

the preceding section, the first moment

of the area with respect

to the x axis is represented by the integral

y dA, which extends

over the entire area A. Dividing A into its component parts A

, A

we write

y dA 5

y dA 1

y dA

or, recalling the second of Eqs. (A.3),

5 A

1 A

where y

, y

, and y

represent the ordinates of the centroids of the

com ponent areas. Extending this result to an arbitrary number of

compo nent areas, and noting that a similar expression may be

obtained for

, we write





(A.5)

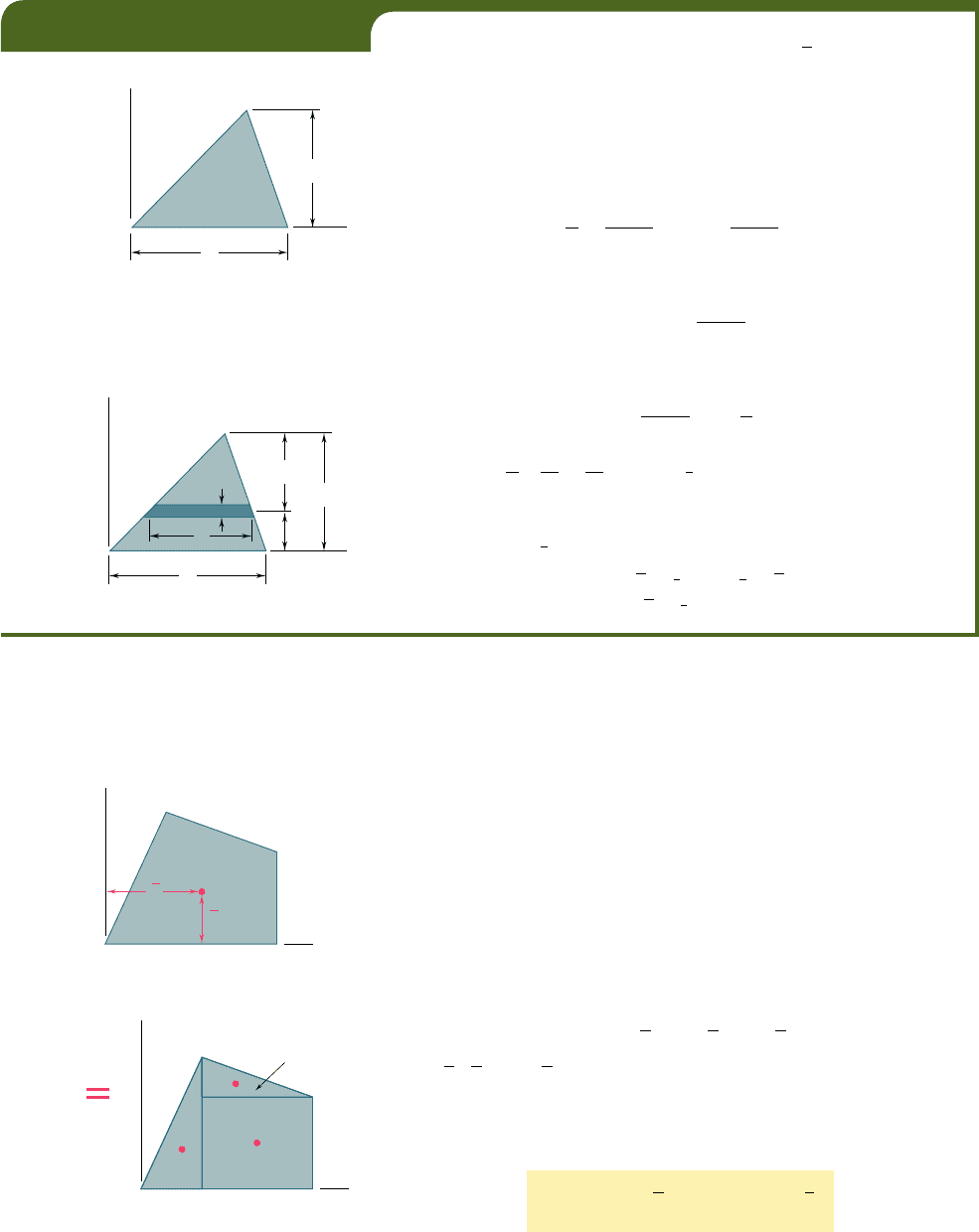
For the triangular area of Fig. A.7, determine (a) the first moment

the area with respect to the x axis, (b) the ordinate

y of the centroid of

the area.

(a) First Moment Q

. We select as an element of area a horizon-

tal strip of length u and thickness dy, and note that all the points within

the element are at the same distance y from the x axis (Fig. A.8). From

similar triangles, we have

2 y

u 5 b

2 y

and

dA 5 u dy 5 b

2 y

The first moment of the area with respect to the x axis is

y dA 5

h 2 y

dy 5

1hy 2 y

2 dy

Q

(b) Ordinate of Centroid. Recalling the first of Eqs. (A.4) and

observing that

bh, we have

5 Ay

5 1

bh2y

y 5

EXAMPLE A.01

Fig. A.7

h – y

Fig. A.8

Fig. A.9

bee80288_app_A1-A30.indd Page A4 11/19/10 6:02:27 PM user-f499bee80288_app_A1-A30.indd Page A4 11/19/10 6:02:27 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app

Apago PDF Enhancer

To obtain the coordinates

and

of the centroid C of the

composite area A, we substitute Q

5 AY and Q

5 A

into Eqs.

(A.5). We have

Y 5





AX 5

Solving for

and

and recalling that the area A is the sum of the

component areas A

, we write

X 5

Y 5

(A.6)

A.2 Centroid of a Composite Area

EXAMPLE A.02

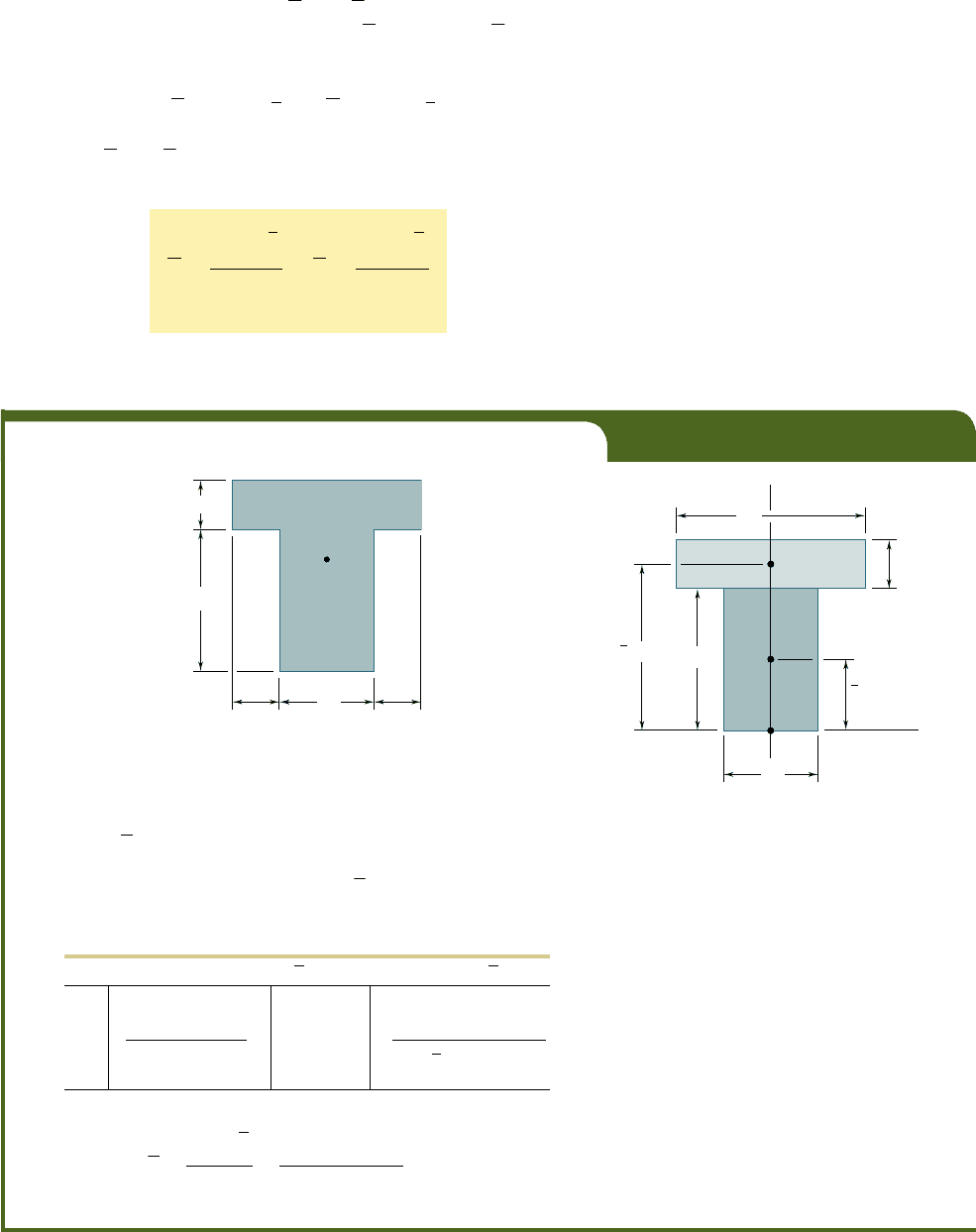
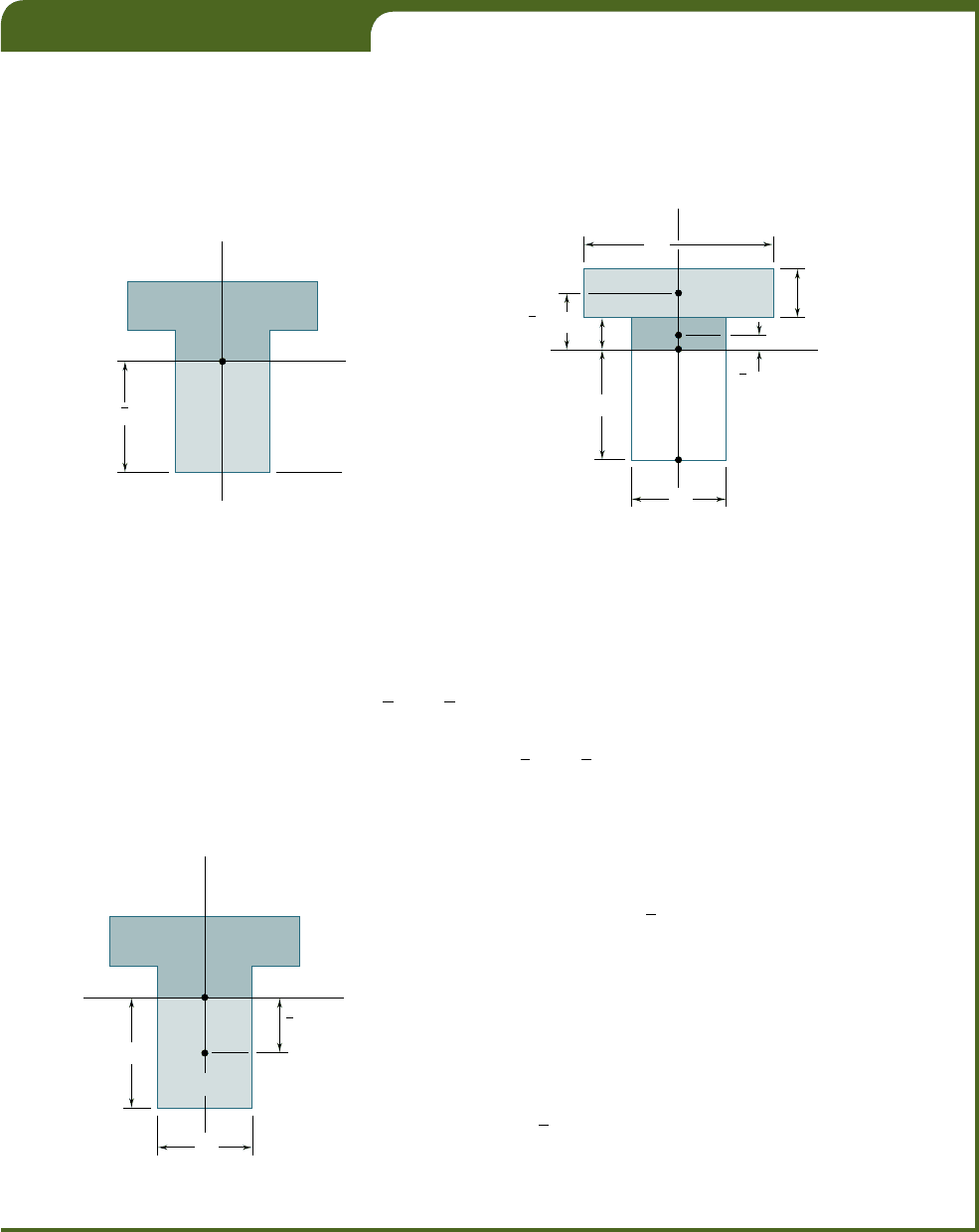
Locate the centroid C of the area A shown in Fig. A.10.

Dimensions in mm

Fig. A.10

Dimensions in mm

 70

 30

Fig. A.11

Selecting the coordinate axes shown in Fig. A.11, we note that the

centroid C must be located on the y axis, since this axis is an axis of sym-

metry; thus,

Dividing A into its component parts

and

, we use the second

of Eqs. (A.6) to determine the ordinate

of the centroid. The actual

computation is best carried out in tabular form.

184 3 10

4 3 10

5 46 mm

Area, mm

, mm

(20)(80) 5 1600 70 112 3 10

(40)(60) 5 2400 30 72 3 10

5 4000

5 184 3 10

bee80288_app_A1-A30.indd Page A5 11/19/10 6:02:33 PM user-f499bee80288_app_A1-A30.indd Page A5 11/19/10 6:02:33 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app

Apago PDF Enhancer

Referring to the area A of Example A.02, we consider the hori-

zontal

¿ axis through its centroid C. (Such an axis is called a

centroidal axis.) Denoting by

¿ the portion of A located above

that axis (Fig. A.12), determine the first moment of

¿ with

respect to the

¿ axis.

EXAMPLE A.03

Solution. We divide the area

¿ into its components A

and

(Fig. A.13). Recalling from Example A.02 that C is located

46 mm above the lower edge of A, we determine the ordinates

y¿

and y¿

of A

and A

and express the first moment Q¿

x¿

¿ with

respect to

¿ as follows:

x¿

5 A

1 A

20 3 80

14 3 40

5 42.3 3 10

Alternative Solution. We first note that since the centroid

C of A is located on the

¿ axis, the first moment

x¿

of the entire

area A with respect to that axis is zero:

x¿

5 Ay¿ 5 A

5 0

Denoting by

– the portion of A located below the

¿ axis and

by Q–

x¿

its first moment with respect to that axis, we have

therefore

x¿

5 Q

x¿

1 Q

–

x¿

5 0orQ

x¿

52Q

–

x¿

which shows that the first moments of

¿ and

– have the same

magnitude and opposite signs. Referring to Fig. A.14, we write

Q–

x¿

5 A

y¿

5 140 3 462122325242.3 3 10

and

Q¿

x¿

52Q–

x¿

5142.3 3 10

Fig. A.12

Fig. A.13

Dimensions in mm

 24

 7

Fig. A.14

A''  A

Dimensions in mm

 23

bee80288_app_A1-A30.indd Page A6 11/19/10 6:02:38 PM user-f499bee80288_app_A1-A30.indd Page A6 11/19/10 6:02:38 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app

Apago PDF Enhancer

A.3 SECOND MOMENT, OR MOMENT OF INERTIA,

OF AN AREA; RADIUS OF GYRATION

Consider again an area A located in the xy plane (Fig. A.1) and the

element of area dA of coordinates x and y. The second moment, or

moment of inertia, of the area A with respect to the x axis, and the

second moment, or moment of inertia, of A with respect to the y

axis are defined, respectively, as

dAI

(A.7)

These integrals are referred to as rectangular moments of inertia,

since they are computed from the rectangular coordinates of the

element dA. While each integral is actually a double integral, it is

possible in many applications to select elements of area dA in the

shape of thin horizontal or vertical strips, and thus reduce the com-

putations to integrations in a single variable. This is illustrated in

Example A.04.

We now define the polar moment of inertia of the area A with

respect to point O (Fig. A.15) as the integral

(A.8)

where

is the distance from O to the element dA. While this integral

is again a double integral, it is possible in the case of a circular area

to select elements of area dA in the shape of thin circular rings, and

thus reduce the computation of

to a single integration (see Exam-

ple A.05).

We note from Eqs. (A.7) and (A.8) that the moments of inertia

of an area are positive quantities. If SI units are used, moments of

inertia are expressed in

; if U.S. customary units are used,

they are expressed in f

or i

An important relation may be established between the polar

moment of inertia

of a given area and the rectangular moments

of inertia I

and I

of the same area. Noting that r

5 x

1 y

, we

write

dA 5

1 y

2 dA 5

dA 1

5 I

1 I

(A.9)

The radius of gyration of an area A with respect to the x axis

is defined as the quantity r

, that satisfies the relation

5 r

A (A.10)

A.3 Second Moment, or Moment of

Inertia, of an Area

Fig. A.1 (repeated)



Fig. A.15

bee80288_app_A1-A30.indd Page A7 11/19/10 6:02:46 PM user-f499bee80288_app_A1-A30.indd Page A7 11/19/10 6:02:46 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app

Apago PDF Enhancer

Moments of Areas

where I

is the moment of inertia of A with respect to the x axis.

Solving Eq. (A.10) for r

, we have

(A.11)

In a similar way, we define the radii of gyration with respect to the

y axis and the origin O. We write

5 r

(A.12)

5 r

(A.13)

Substituting for

, I

, and I

in terms of the corresponding radii of

gyration in Eq. (A.9), we observe that

5 r

1 r

(A.14)

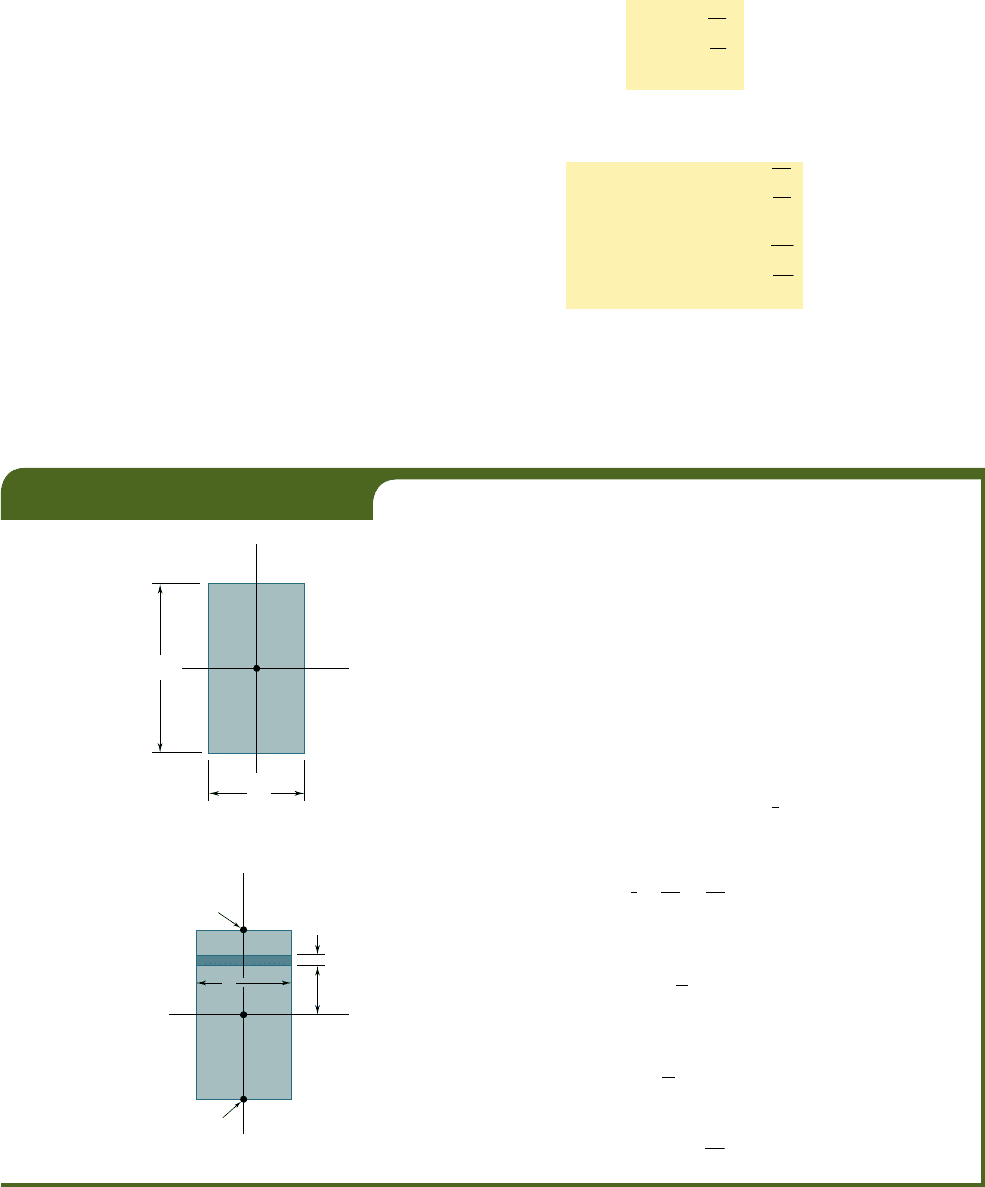
For the rectangular area of Fig. A.16, determine (a) the moment of inertia

of the area with respect to the centroidal x axis, (b) the corresponding

radius of gyration r

(a) Moment of Inertia I

. We select as an element of area a

horizontal strip of length b and thickness dy (Fig. A.17). Since all the

points within the strip are at the same distance y from the x axis, the

moment of inertia of the strip with respect to that axis is

5 y

dA 5 y

1b dy2

Integrating from y 52

2 to y 51

2, we write

dA 5

1b dy25

b3y

(b) Radius of Gyration r

. From Eq. (A.10), we have

5 r

A

5 r

and, solving for

5 h

EXAMPLE A.04

Fig. A.16

Fig. A.17

 h/2

 h/2

bee80288_app_A1-A30.indd Page A8 11/19/10 6:02:49 PM user-f499bee80288_app_A1-A30.indd Page A8 11/19/10 6:02:49 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/app