Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

687

REVIEW PROBLEMS

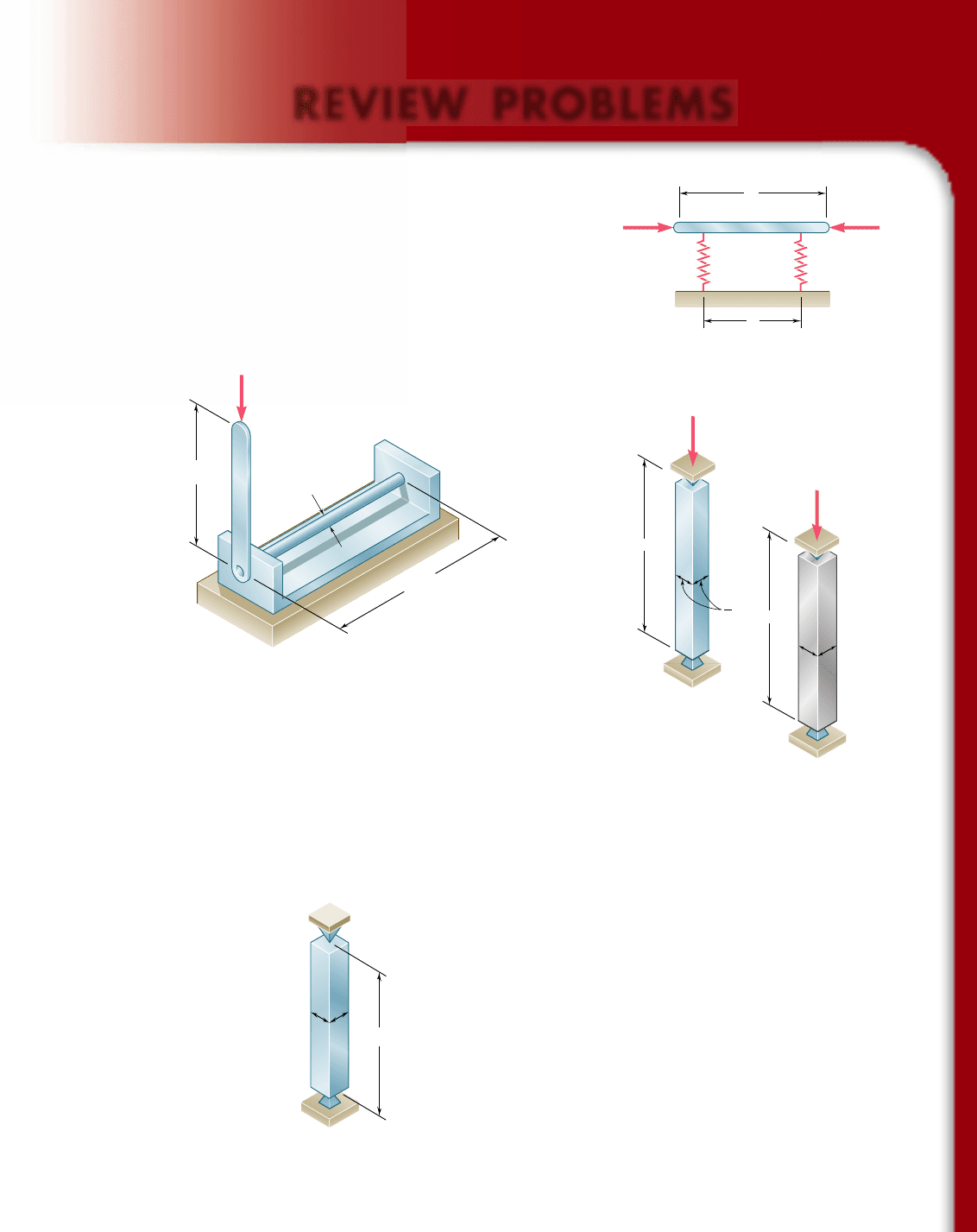
10.117 The rigid bar AD is attached to two springs of constant k and is

in equilibrium in the position shown. Knowing that the equal and

opposite loads P and P9 remain horizontal, determine the magni-

tude P

of the critical load for the system.

10.118 The steel rod BC is attached to the rigid bar AB and to the fixed

support at C. Knowing that G 5 11.2 3 10

psi, determine the

diameter of rod BC for which the critical load P

of the system is

80 lb.

Fig. P10.117

15 in.

20 in.

Fig. P10.118

10.119 Determine (a) the critical load for the steel strut, (b) the dimension

d for which the aluminum strut will have the same critical load.

weight of the steel strut.

10.120 Supports A and B of the pin-ended column shown are at a fixed

distance L from each other. Knowing that at a temperature T

the force in the column is zero and that buckling occurs when the

temperature is T

5 T

1 DT, express DT in terms of b, L and the

coefficient of thermal expansion a.

in.

4 ft

Steel

E  29  10

psi



 490 lb/ft

Aluminum

E  10.1  10

psi



 170 lb/ft

Fig. P10.119

Fig. P10.120

bee80288_ch10_630-691.indd Page 687 11/1/10 2:39:46 PM user-f499bee80288_ch10_630-691.indd Page 687 11/1/10 2:39:46 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

688

Columns

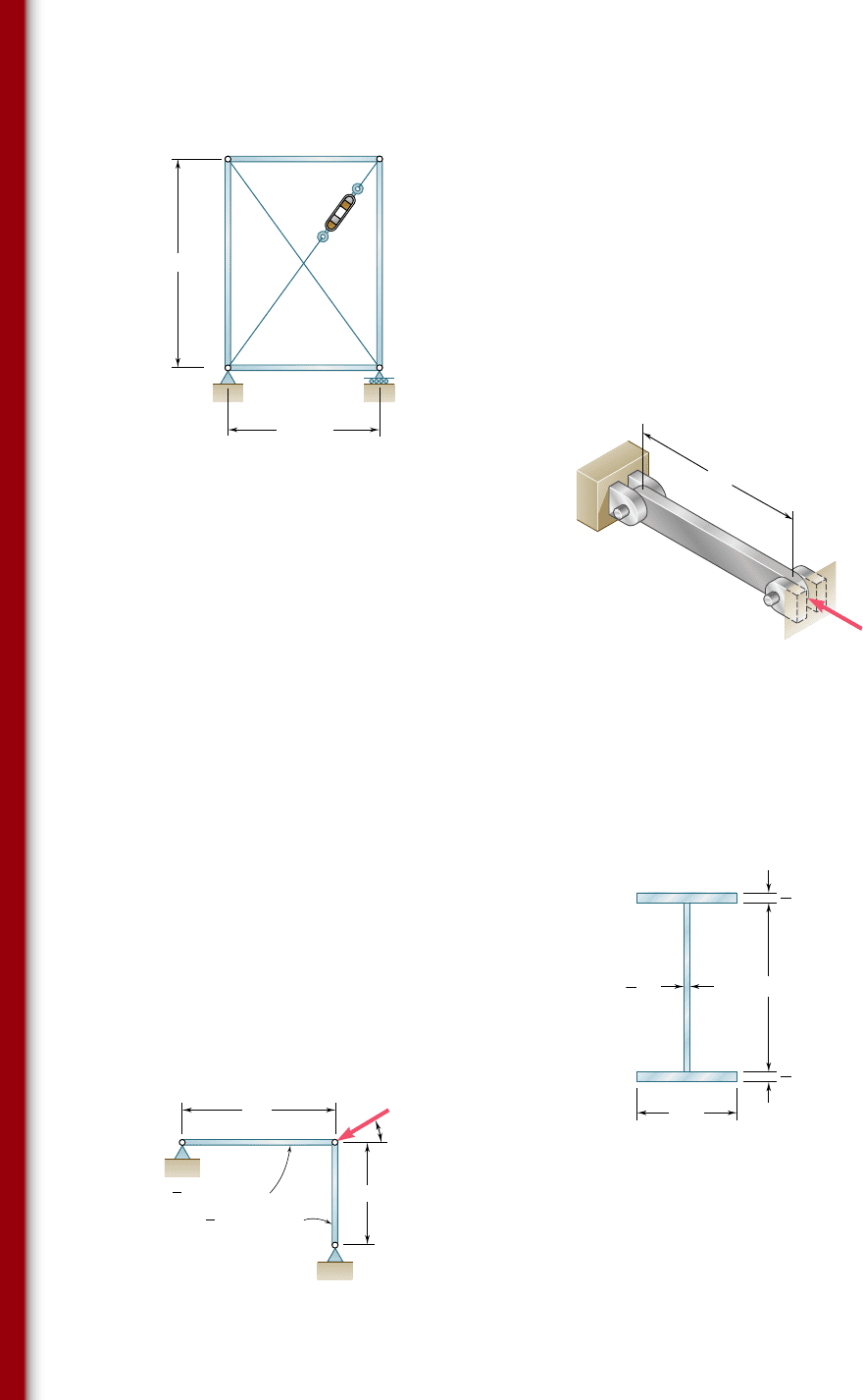
10.121 Members AB and CD are 30-mm-diameter steel rods, and members

BC and AD are 22-mm-diameter steel rods. When the turnbuckle

is tightened, the diagonal member AC is put in tension. Knowing

that a factor of safety with respect to buckling of 2.75 is required,

determine the largest allowable tension in AC. Use E 5 200 GPa

and consider only buckling in the plane of the structure.

10.122 The uniform aluminum bar AB has a 20 3 36-mm rectangular

cross section and is supported by pins and brackets as shown. Each

end of the bar may rotate freely about a horizontal axis through the

pin, but rotation about a vertical axis is prevented by the brackets.

Using E 5 70 GPa, determine the allowable centric load P if a

factor of safety of 2.5 is required.

2.25 m

3.5 m

Fig. P10.121

2 m

Fig. P10.122

10.123 A column with the cross section shown has a 13.5-ft effective

length. Using allowable stress design, determine the largest cen-

tric load that can be applied to the column. Use s

5 36 ksi and

E 5 29 3 10

psi.

10 in.

6 in.

in.

Fig. P10.123

-in. diameter

3 ft

2 ft

Fig. P10.124

10.124 (a) Considering only buckling in the plane of the structure shown

and using Euler’s formula, determine the value of u between 0 and

908 for which the allowable magnitude of the load P is maximum.

(b) Determine the corresponding maximum value of P knowing

that a factor of safety of 3.2 is required. Use E 5 29 3 10

psi.

bee80288_ch10_630-691.indd Page 688 11/1/10 2:40:40 PM user-f499bee80288_ch10_630-691.indd Page 688 11/1/10 2:40:40 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

689

Review Problems

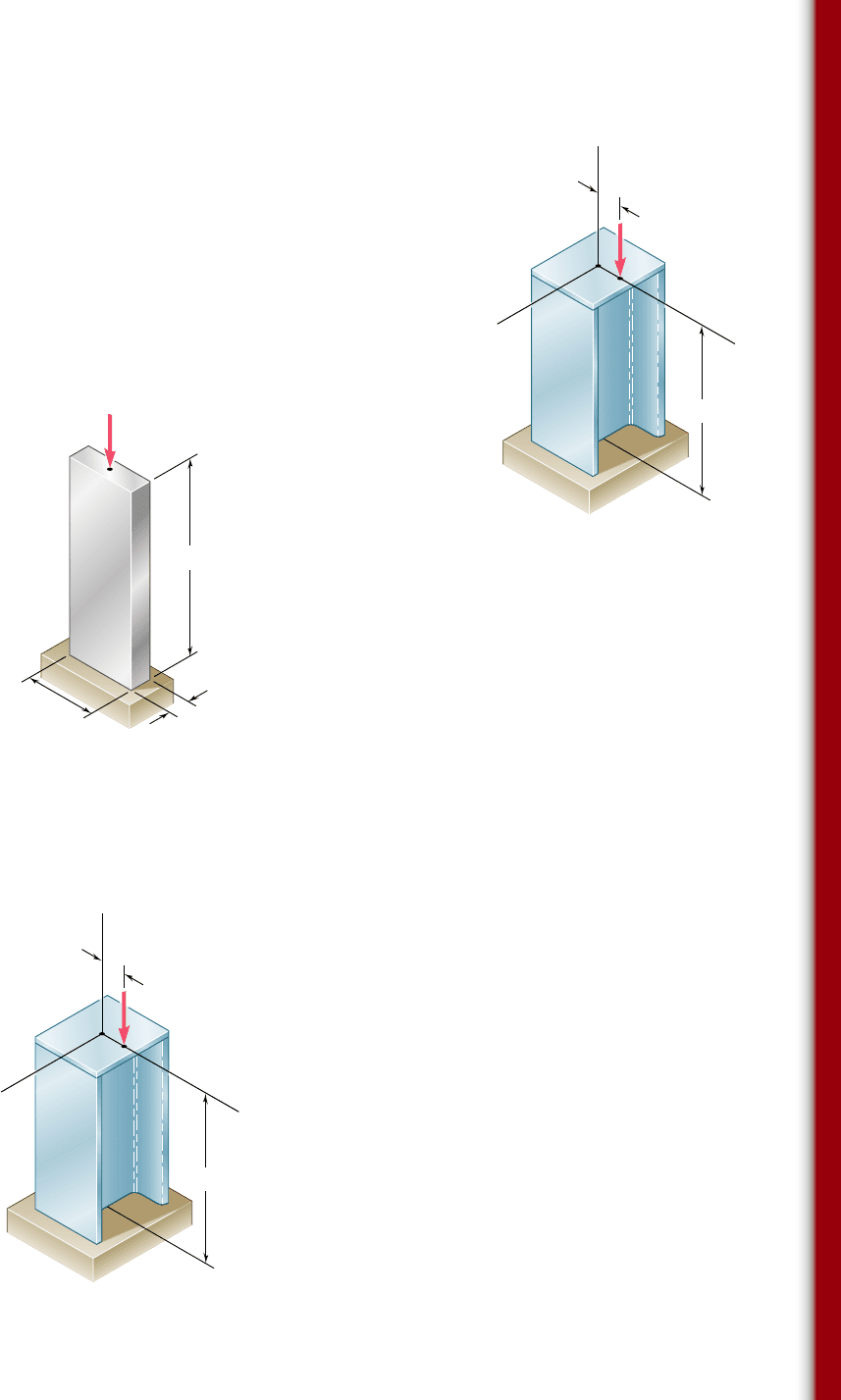
10.125 An axial load P of magnitude 560 kN is applied at a point on the

x axis at a distance e 5 6 mm from the geometric axis of the

W200 3 46.1 rolled-steel column BC. Using E 5 200 GPa, deter-

mine (a) the horizontal deflection of end C, (b) the maximum stress

in the column.

10.126 A column of 17-ft effective length must carry a centric load of

235 kips. Using allowable stress design, select the wide-flange

shape of 10-in. nominal depth that should be used. Use s

5 36 ksi

and E 5 29 3 10

psi.

10.127 Bar AB is free at its end A and fixed at its base B. Determine

the allowable centric load P if the aluminum alloy is (a) 6061-T6,

(b) 2014-T6.

200  46.1

2.3 m

Fig. P10.125

85 mm

30 mm

10 mm

Fig. P10.127

10.128 A 43-kip axial load P is applied to the rolled-steel column BC at

a point on the x axis at a distance e 5 2.5 in. from the geometric

axis of the column. Using the allowable-stress method, select the

wide-flange shape of 8-in. nominal depth that should be used. Use

E 5 29 3 10

psi and s

5 36 ksi.

8 ft

Fig. P10.128

bee80288_ch10_630-691.indd Page 689 11/1/10 2:40:52 PM user-f499bee80288_ch10_630-691.indd Page 689 11/1/10 2:40:52 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

690

COMPUTER PROBLEMS

The following problems are designed to be solved with a computer.

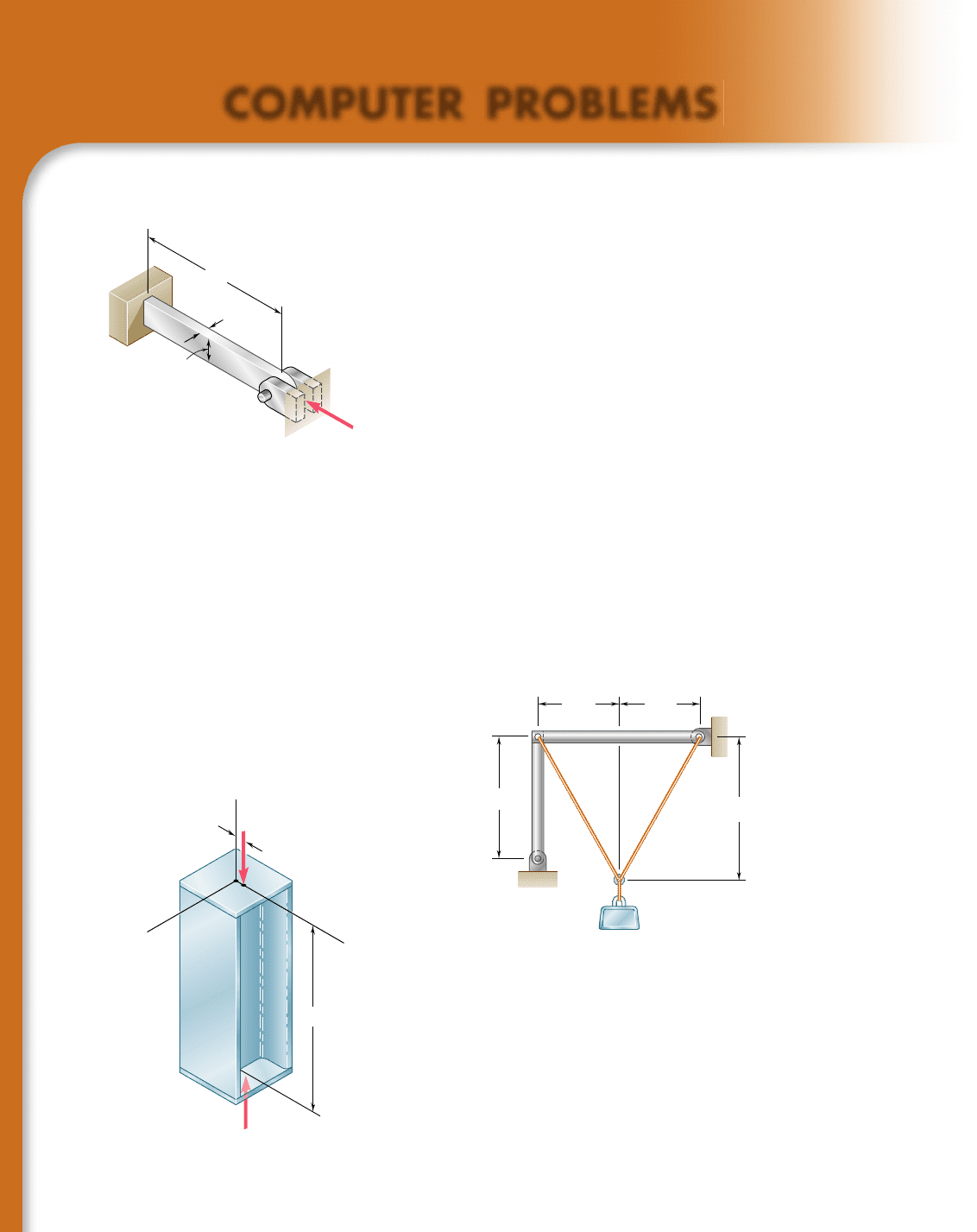
10.C1 A solid steel rod having an effective length of 500 mm is to be

used as a compression strut to carry a centric load P. For the grade of steel

used, E 5 200 GPa and s

5 245 MPa. Knowing that a factor of safety of

2.8 is required and using Euler’s formula, write a computer program and

use it to calculate the allowable centric load P

all

for values of the radius of

the rod from 6 mm to 24 mm, using 2-mm increments.

10.C2 An aluminum bar is fixed at end A and supported at end B so that

it is free to rotate about a horizontal axis through the pin. Rotation about a

vertical axis at end B is prevented by the brackets. Knowing that E 5 10.1 3

psi, use Euler’s formula with a factor of safety of 2.5 to determine the

allowable centric load P for values of b from 0.75 in. to 1.5 in., using 0.125-in.

increments.

10.C3 The pin-ended members AB and BC consist of sections of alumi-

num pipe of 120-mm outer diameter and 10-mm wall thickness. Knowing

that a factor of safety of 3.5 is required, determine the mass m of the largest

block that can be supported by the cable arrangement shown for values of

h from 4 m to 8 m, using 0.25-m increments. Use E 5 70 GPa and consider

only buckling in the plane of the structure.

1.5 in.

6 ft

Fig. P10.C2

3 m

4 m

3 m

Fig. P10.C3

10.C4 An axial load P is applied at a point located on the x axis at a dis-

tance e 5 0.5 in. from the geometric axis of the W8 3 40 rolled-steel col-

umn AB. Using E 5 29 3 10

psi, write a computer program and use it to

calculate for values of P from 25 to 75 kips, using 5-kip increments, (a) the

horizontal deflection at the midpoint C, (b) the maximum stress in the

column.

8  40

18.4 ft

Fig. P10.C4

bee80288_ch10_630-691.indd Page 690 11/1/10 2:41:00 PM user-f499bee80288_ch10_630-691.indd Page 690 11/1/10 2:41:00 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

691

Computer Problems

10.C5 A column of effective length L is made from a rolled-steel shape

and carries a centric axial load P. The yield strength for the grade of steel

used is denoted by s

, the modulus of elasticity by E, the cross-sectional

area of the selected shape by A, and its smallest radius of gyration by r.

Using the AISC design formulas for allowable stress design, write a com-

puter program that can be used with either SI or U.S. customary units to

determine the allowable load P. Use this program to solve (a) Prob. 10.57,

(b) Prob. 10.58, (c) Prob. 10.60.

10.C6 A column of effective length L is made from a rolled-steel shape

and is loaded eccentrically as shown. The yield strength of the grade of

steel used is denoted by s

, the allowable stress in bending by s

all

, the

modulus of elasticity by E, the cross-sectional area of the selected shape

by A, and its smallest radius of gyration by r. Write a computer program

that can be used with either SI or U.S. customary units to determine the

allowable load P, using either the allowable-stress method or the interaction

method. Use this program to check the given answer for (a) Prob. 10.113,

(b) Prob. 10.114.

Fig. P10.C6

bee80288_ch10_630-691.indd Page 691 11/1/10 2:41:10 PM user-f499bee80288_ch10_630-691.indd Page 691 11/1/10 2:41:10 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

As the diver comes down on the diving

board the potential energy due to his

elevation above the board will be

converted into strain energy due to

the bending of the board. The normal

and shearing stresses resulting from

energy loadings will be determined

in this chapter.

692

bee80288_ch11_692-758.indd Page 692 11/12/10 5:10:20 PM user-f499bee80288_ch11_692-758.indd Page 692 11/12/10 5:10:20 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer

CHAPTER

693

Energy Methods

bee80288_ch11_692-758.indd Page 693 11/12/10 5:12:13 PM user-f499bee80288_ch11_692-758.indd Page 693 11/12/10 5:12:13 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer

694

Chapter 11 Energy Methods

11.1 Introduction

11.2 Strain Energy

11.3 Strain-Energy Density

11.4 Elastic Strain Energy for Normal

Stresses

11.5 Elastic Strain Energy for Shearing

Stresses

11.6 Strain Energy for a General

State of Stress

11.7 Impact Loading

11.8 Design for Impact Loads

11.9 Work and Energy under a

Single Load

11.10 Deflection under a Single Load

By the Work-Energy Method

*11.11 Work and Energy under Several

Loads

*11.12 Castigliano’s Theorem

*11.13 Deflections by Castigliano’s

Theorem

*11.14 Statically Indeterminate Structures

11.1 INTRODUCTION

In the previous chapter we were concerned with the relations exist-

ing between forces and deformations under various loading condi-

tions. Our analysis was based on two fundamental concepts, the

concept of stress (Chap. 1) and the concept of strain (Chap. 2). A

third important concept, the concept of strain energy, will now be

introduced.

In Sec. 11.2, the strain energy of a member will be defined as

the increase in energy associated with the deformation of the mem-

ber. You will see that the strain energy is equal to the work done by

a slowly increasing load applied to the member. The strain-energy

density of a material will be defined as the strain energy per unit

volume; it will be seen that it is equal to the area under the stress-

strain diagram of the material (Sec. 11.3). From the stress-strain

diagram of a material two additional properties will be defined,

namely, the modulus of toughness and the modulus of resilience of

the material.

In Sec. 11.4 the elastic strain energy associated with normal

stresses will be discussed, first in members under axial loading and

then in members in bending. Later you will consider the elastic

strain energy associated with shearing stresses such as occur in tor-

sional loadings of shafts and in transverse loadings of beams (Sec.

11.5). Strain energy for a general state of stress will be considered

in Sec. 11.6, where the maximum-distortion-energy criterion for

yielding will be derived.

The effect of impact loading on members will be considered

in Sec. 11.7. You will learn to calculate both the maximum stress and

the maximum deflection caused by a moving mass impacting on a

member. Properties that increase the ability of a structure to with-

stand impact loads effectively will be discussed in Sec. 11.8.

In Sec. 11.9 the elastic strain of a member subjected to a

single concentrated load will be calculated, and in Sec. 11.10 the

deflection at the point of application of a single load will be

determined.

The last portion of the chapter will be devoted to the determi-

nation of the strain energy of structures subjected to several loads

(Sec. 11.11). Castigliano’s theorem will be derived in Sec. 11.12 and

used in Sec. 11.13 to determine the deflection at a given point of a

structure subjected to several loads. In the last section Castigliano’s

theorem will be applied to the analysis of indeterminate structures

(Sec. 11.14).

11.2 STRAIN ENERGY

Consider a rod BC of length L and uniform cross-sectional area A,

which is attached at B to a fixed support, and subjected at C to a

slowly increasing axial load P (Fig. 11.1). As we noted in Sec. 2.2,

by plotting the magnitude P of the load against the deformation x of

the rod, we obtain a certain load-deformation diagram (Fig. 11.2)

that is characteristic of the rod BC.

Fig. 11.1 Axially loaded rod.

bee80288_ch11_692-758.indd Page 694 11/12/10 5:12:18 PM user-f499bee80288_ch11_692-758.indd Page 694 11/12/10 5:12:18 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

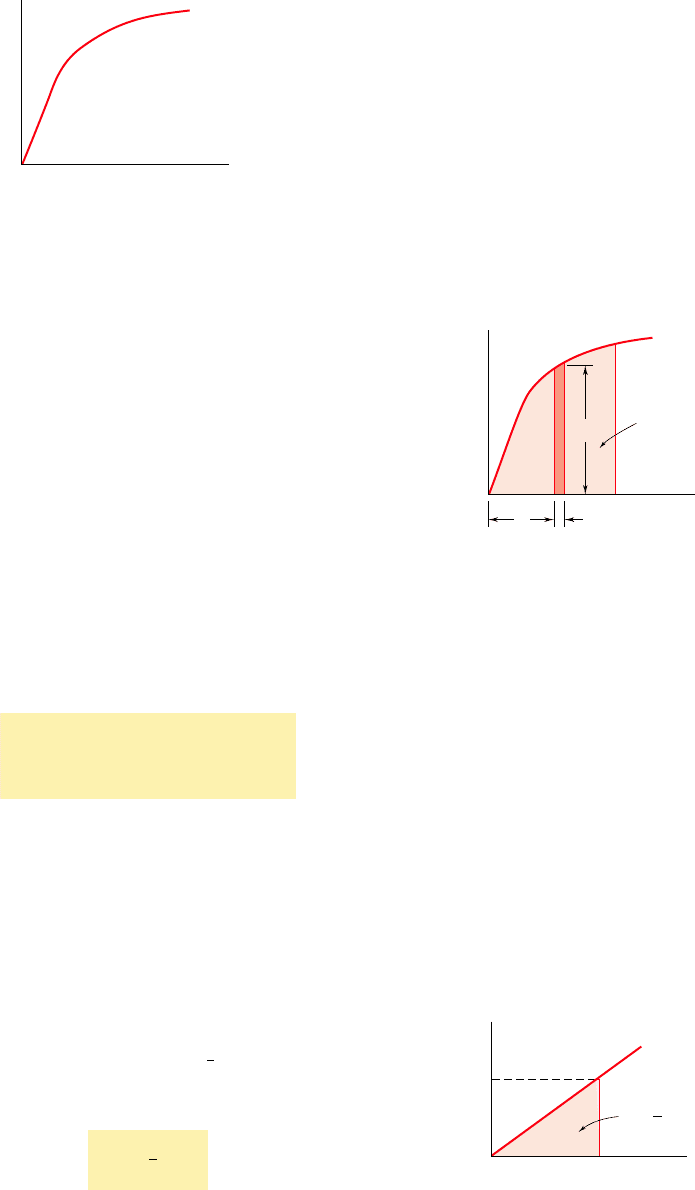
Apago PDF Enhancer

695

11.2 Strain Energy

Let us now consider the work dU done by the load P as the

rod elongates by a small amount dx. This elementary work is equal

to the product of the magnitude P of the load and of the small elon-

gation dx. We write

dU 5 P dx (11.1)

and note that the expression obtained is equal to the element of area

of width dx located under the load-deformation diagram (Fig. 11.3).

The total work U done by the load as the rod undergoes a deforma-

tion x

is thus

U 5

P dx

and is equal to the area under the load-deformation diagram between

x 5 0 and x 5 x

The work done by the load P as it is slowly applied to the rod

must result in the increase of some energy associated with the defor-

mation of the rod. This energy is referred to as the strain energy of

the rod. We have, by definition,

Strain energy 5 U 5

P dx

(11.2)

We recall that work and energy should be expressed in units

obtained by multiplying units of length by units of force. Thus, if SI

metric units are used, work and energy are expressed in N ? m; this

unit is called a joule (J). If U.S. customary units are used, work and

energy are expressed in ft ? lb or in in ? lb.

In the case of a linear and elastic deformation, the portion of

the load-deformation diagram involved can be represented by a

straight line of equation P 5 kx (Fig. 11.4). Substituting for P in Eq.

(11.2), we have

U 5

kx dx 5

U 5

(11.3)

where P

is the value of the load corresponding to the deformation x

Fig. 11.2 Load-deformation diagram.

U  Are

Fig. 11.3 Work due to load P.

P  kx

U  P

Fig. 11.4 Work due to linear,

elastic deformation.

bee80288_ch11_692-758.indd Page 695 11/12/10 5:12:23 PM user-f499bee80288_ch11_692-758.indd Page 695 11/12/10 5:12:23 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11

Apago PDF Enhancer

696

Energy Methods

The concept of strain energy is particularly useful in the deter-

mination of the effects of impact loadings on structures or machine

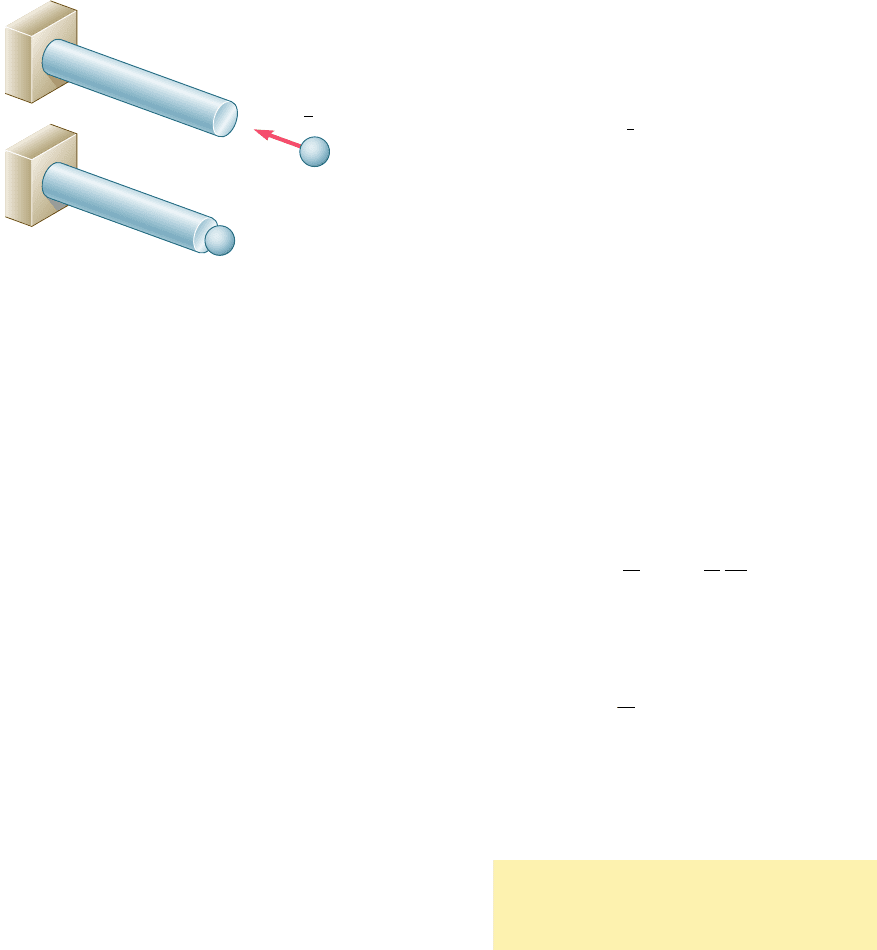
components. Consider, for example, a body of mass m moving with

a velocity v

which strikes the end B of a rod AB (Fig. 11.5a).

Neglecting the inertia of the elements of the rod, and assuming no

dissipation of energy during the impact, we find that the maximum

strain energy U

acquired by the rod (Fig. 11.5b) is equal to the

original kinetic energy T 5

of the moving body. We then deter-

mine the value P

of the static load which would have produced the

same strain energy in the rod, and obtain the value s

of the largest

stress occurring in the rod by dividing P

by the cross-sectional area

of the rod.

11.3 STRAIN-ENERGY DENSITY

As we noted in Sec. 2.2, the load-deformation diagram for a rod BC

depends upon the length L and the cross-sectional area A of the rod.

The strain energy U defined by Eq. (11.2), therefore, will also depend

upon the dimensions of the rod. In order to eliminate the effect of size

from our discussion and direct our attention to the properties of the

material, the strain energy per unit volume will be considered. Dividing

the strain energy U by the volume V 5 AL of the rod (Fig. 11.1), and

using Eq. (11.2), we have

Recalling that PyA represents the normal stress s

in the rod,

and x/L the normal strain P

, we write

where P

denotes the value of the strain corresponding to the elonga-

tion x

. The strain energy per unit volume, UyV, is referred to as the

strain-energy density and will be denoted by the letter u. We have,

therefore,

Strain-energy density 5 u 5

(11.4)

The strain-energy density u is expressed in units obtained by divid-

ing units of energy by units of volume. Thus, if SI metric units are

used, the strain-energy density is expressed in J/m

or its multiples

kJ/m

and MJ/m

; if U.S. customary units are used, it is expressed

in in ? lb/in

.†

U  0

 0



T 

U  U





T  0

v  0

(a)

(b)

Fig. 11.5 Rod subject to impact loading.

†We note that 1 J/m

and 1 Pa are both equal to 1 N/m

, while 1 in ? lb/in

and 1 psi are

both equal to 1 lb/in

. Thus, strain-energy density and stress are dimensionally equal and

could be expressed in the same units.

bee80288_ch11_692-758.indd Page 696 11/12/10 5:12:29 PM user-f499bee80288_ch11_692-758.indd Page 696 11/12/10 5:12:29 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch11