Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

677

centric loading of Fig. 10.34a and to the pure bending of

Fig. 10.34b. We have

all

centric

all

bendin

# 1

(10.55)

The type of formula obtained is known as an interaction formula.

We note that, when M 5 0, the use of this formula results in

the design of a centrically loaded column by the method of Sec. 10.6.

On the other hand, when P 5 0, the use of the formula results in

the design of a beam in pure bending by the method of Chap. 4.

When P and M are both different from zero, the interaction formula

results in a design that takes into account the capacity of the member

to resist bending as well as axial loading. In all cases, (s

all

)

centric

will

be determined by using the largest slenderness ratio of the column,

regardless of the plane in which bending takes place.†

When the eccentric load P is not applied in a plane of sym-

metry of the column, it causes bending about both of the principal

axes of the cross section. We recall from Sec. 4.14 that the load P

can then be replaced by a centric load P and two couples repre-

sented by the couple vectors M

and M

shown in Fig. 10.35. The

interaction formula to be used in this case is

all

centric

ƒ M

ƒ z

max

all

bendin

ƒ M

ƒ x

max

all

bendin

# 1

(10.56)

10.7 Design of Columns under an

Eccentric Load

†This procedure is required by all major codes for the design of steel, aluminum, and

timber compression members. In addition, many specifications call for the use of an

additional factor in the second term of Eq. (10.55); this factor takes into account the

additional stresses resulting from the deflection of the column due to bending.

EXAMPLE 10.05

Use the interaction method to determine the maximum load P that can

be safely supported by the column of Example 10.04 with an eccentricity

of 0.8 in. The allowable stress in bending is 24 ksi.

The value of (s

all

)

centric

has already been determined in Example

10.04. We have

all

centric

5 19.79 ksi

all

bending

5 24 ksi

Substituting these values into Eq. (10.55), we write

79 k

24 k

# 1.0

Using the numerical data from Example 10.04, we write

79 k

0.8

1.0

1.33

24 k

# 1.0

P # 26.6

ips

The maximum load that can be safely applied is thus P 5 26.6 kips.

Fig. 10.35 Column with eccentric load.

bee80288_ch10_630-691.indd Page 677 11/1/10 2:38:38 PM user-f499bee80288_ch10_630-691.indd Page 677 11/1/10 2:38:38 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

678

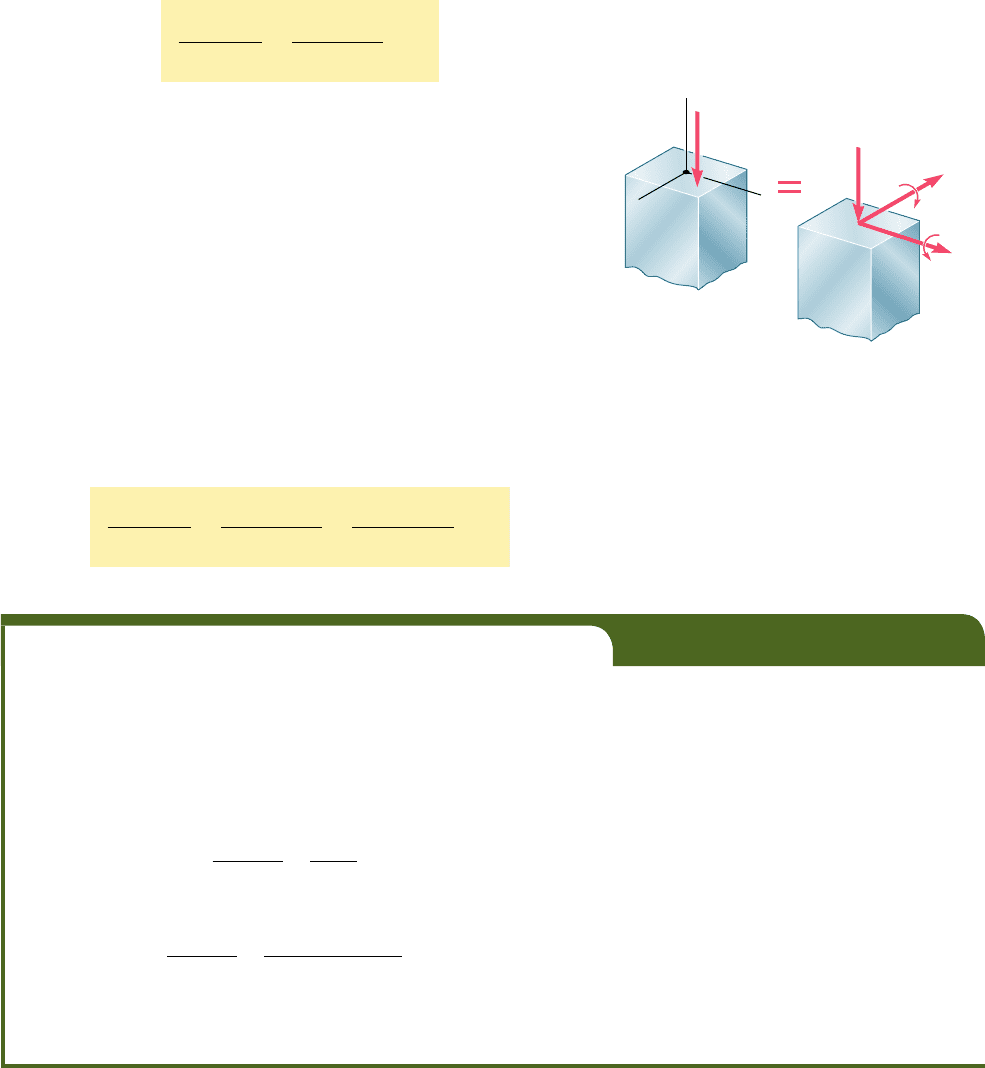
SAMPLE PROBLEM 10.5

Using the allowable-stress method, determine the largest load P that can be

safely carried by a W310 3 74 steel column of 4.5-m effective length. Use

E 5 200 GPa and s

5 250 MPa.

SOLUTION

The largest slenderness ratio of the column is Lyr

5 (4.5 m)y(0.0498 m) 5

90.4. Using Eq. (10.41) with E 5 200 GPa and s

5 250 MPa, we find that

the slenderness ratio at the junction between the two equations for s

Lyr 5 133.2. Thus, we use Eqs. (10.38) and (10.39) and find that s

162.2 MPa. Using Eq. (10.42), the allowable stress is

all

centric

5 162.2

1.67 5 97.1 MPa

For the given column and loading, we have

42 3 10

0.200 m

050 3 10

Substituting into Eq. (10.58), we write

# s

all

42 3 10

0.200 m

1.050 3 10

# 97.1 MPa

P # 327

The largest allowable load P is thus P 5 327 kNw

◀

200 mm

W310 ⫻ 74

A ⫽ 9420 mm

⫽ 132 mm

⫽ 1050 ⫻ 10

⫽ 49.8 mm

200 mm

M ⫽ P(0.200 m)

SAMPLE PROBLEM 10.6

Using the interaction method, solve Sample Prob. 10.5. Assume (s

all

)

bending

150 MPa.

SOLUTION

Using Eq. (10.60), we write

all

centric

all

bending

# 1

Substituting the given allowable bending stress and the allowable centric

stress found in Sample Prob. 10.5, as well as the other given data, we have

19.42 3 10

1 3 10

P10.200 m2

11.050 3 10

150 3 10

# 1

P # 423

The largest allowable load P is thus P = 423 kNw

◀

bee80288_ch10_630-691.indd Page 678 11/20/10 2:57:51 PM user-f499bee80288_ch10_630-691.indd Page 678 11/20/10 2:57:51 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10

Apago PDF Enhancer

679

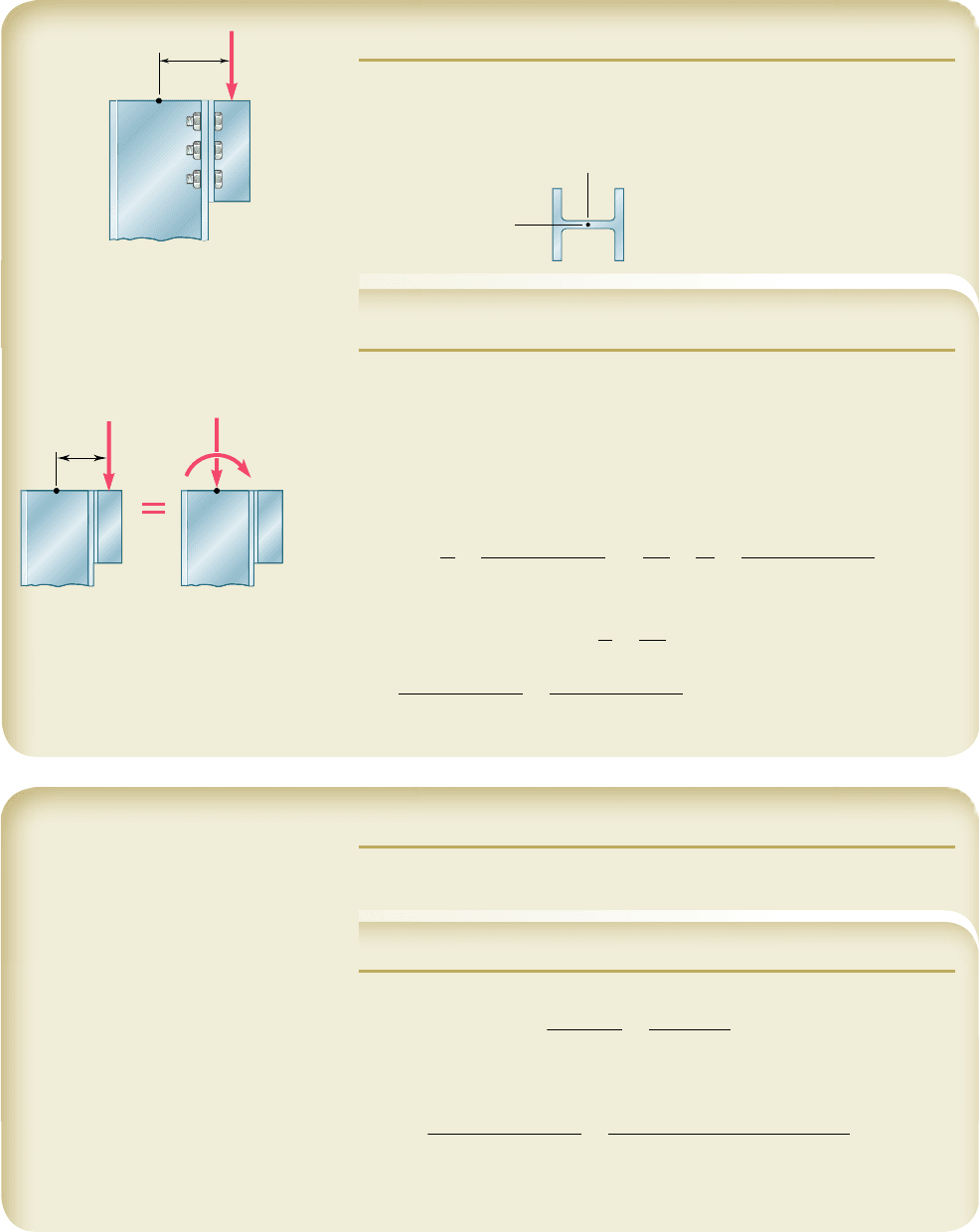
SAMPLE PROBLEM 10.7

A steel column having an effective length of 16 ft is loaded eccentrically as

shown. Using the interaction method, select the wide-flange shape of 8-in.

nominal depth that should be used. Assume E 5 29 3 10

psi and s

5 36 ksi,

and use an allowable stress in bending of 22 ksi.

SOLUTION

So that we can select a trial section, we use the allowable-stress method with

all

5 22 ksi and write

all

(1)

From Appendix C we observe for shapes of 8-in. nominal depth that

and r

< 3.5 in. Substituting into Eq. (1), we have

22 ksi 5

85 kips

425 kip ? in.

4 in.

3.5 in.

< 10.2 in

We select for a first trial shape: W8 3 35.

Trial 1: W8 3 35. The allowable stresses are

Allowable Bending Stress: (see data)

all

bending

5 22 ksi

Allowable Concentric Stress: The largest slenderness ratio of the column

is Lyr

5 (192 in.)y(2.03 in.) 5 94.6. Using Eq. (10.41) with E 5 29 3 10

psi

and s

5 36 ksi, we find that the slenderness ratio at the junction between

the two equations for s

is Lyr 5 133.7. Thus, we use Eqs. (10.38) and (10.39)

and find that s

5 22.5 ksi. Using Eq. (10.42), the allowable stress is

all

centric

5 22.5

1.67 5 13.46 ksi

For the W8 3 35 trial shape, we have

ips

3 in

5 8.25 ksi

425

ip ? in.

31.2 in

5 13.62 ksi

With this data we find that the left-hand member of Eq. (10.60) is

all

centric

all

bending

8.25 ksi

13.46 ksi

13.62 ksi

22 ksi

5 1.232

Since 1.232 . 1.000, the requirement expressed by the interaction formula

is not satisfied; we must select a larger trial shape.

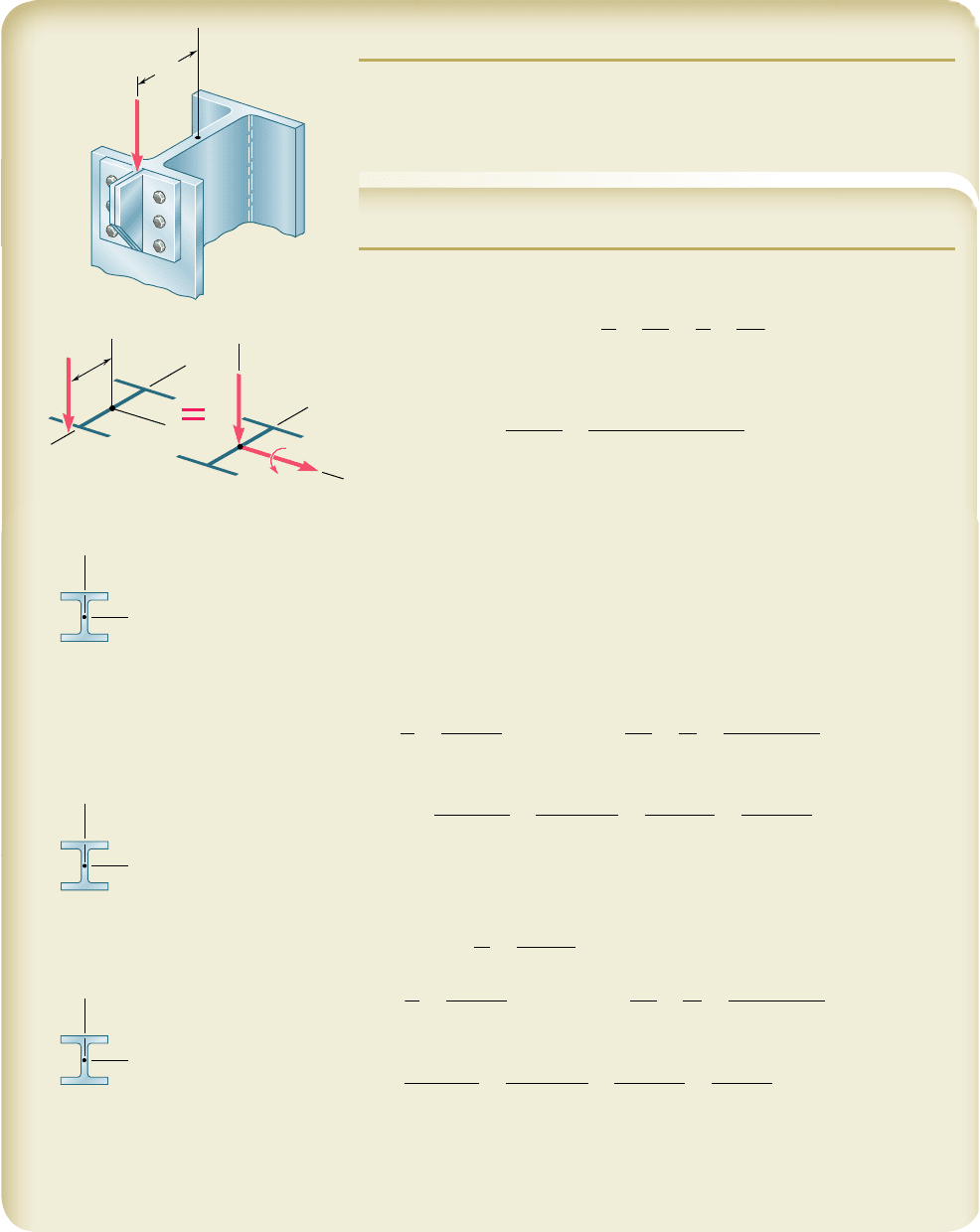
Trial 2: W8 3 48. Following the procedure used in trial 1, we write

192

in.

2.08 in.

5 92.3

all

centric

5 13.76 ksi

ips

1 in

5 6.03 ksi

425

ip ? in.

43.2 in

5 9.84 ksi

Substituting into Eq. (10.60) gives

all

centric

all

bending

6.03 ksi

13.76 ksi

9.82 ksi

22 ksi

5 0.885 , 1.000

The W8 3 48 shape is satisfactory but may be unnecessarily large.

Trial 3: W8 3 40. Following again the same procedure, we find that

the interaction formula is not satisfied.

Selection of Shape. The shape to be used is W8 3 48

◀

5 in.

P ⫽ 85 kips

5 in.

P ⫽ 85 kips

M ⫽ (85 kips)(5 in.)

⫽ 425 kip · in.

W8 ⫻ 35

A ⫽ 10.3 in

⫽ 3.51 in.

⫽ 2.03 in.

⫽ 31.2 in

L ⫽ 16 ft ⫽ 192 in.

W8 ⫻ 48

A ⫽ 14.1 in

⫽ 3.61 in.

⫽ 2.08 in.

⫽ 43.2 in

L ⫽ 16 ft ⫽ 192 in.

W8 ⫻ 40

A ⫽ 11.7 in

⫽ 3.53 in.

⫽ 2.04 in.

⫽ 35.5 in

L ⫽ 16 ft ⫽ 192 in.

bee80288_ch10_630-691.indd Page 679 11/20/10 2:57:59 PM user-f499bee80288_ch10_630-691.indd Page 679 11/20/10 2:57:59 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10

Apago PDF Enhancer

PROBLEMS

680

10.89 An eccentric load is applied at a point 22 mm from the geometric

axis of a 60-mm-diameter rod made of a steel for which s

250 MPa and E 5 200 GPa. Using the allowable-stress method,

determine the allowable load P.

10.90 Solve Prob. 10.89, assuming that the load is applied at a point 40 mm

from the geometric axis and that the effective length is 0.9 m.

10.91 A column of 5.5-m effective length is made of the aluminum alloy

2014-T6, for which the allowable stress in bending is 220 MPa.

Using the interaction method, determine the allowable load P,

knowing that the eccentricity is (a) e 5 0, (b) e 5 40 mm.

22 mm

60 mm diameter

1.2 m

Fig. P10.89

152 mm

15 mm

5.5 m

Fig. P10.91

10.92 Solve Prob. 10.91, assuming that the effective length of the column

is 3.0 m.

10.93 A sawn-lumber column of 5.0 3 7.5-in. cross section has an effec-

tive length of 8.5 ft. The grade of wood used has an adjusted allow-

able stress for compression parallel to the grain s

5 1180 psi and

an adjusted modulus E 5 440 3 10

psi. Using the allowable-stress

method, determine the largest eccentric load P that can be applied

when (a) e 5 0.5 in., (b) e 5 1.0 in.

10.94 Solve Prob. 10.93 using the interaction method and an allowable

stress in bending of 1300 psi.

10.95 A column of 14-ft effective length consists of a section of steel

tubing having the cross section shown. Using the allowable-stress

method, determine the maximum allowable eccentricity e if

(a) P 5 55 kips, (b) P 5 35 kips. Use s

5 36 ksi and E 5

29 3 10

psi.

10.96 Solve Prob. 10.95, assuming that the effective length of the column

is increased to 18 ft and that (a) P 5 28 kips, (b) P 5 18 kips.

7.5 in.

5.0 in.

Fig. P10.93

4 in.

in.

14 ft

Fig. P10.95

bee80288_ch10_630-691.indd Page 680 11/1/10 2:39:01 PM user-f499bee80288_ch10_630-691.indd Page 680 11/1/10 2:39:01 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

681

Problems

10.97 The compression member AB is made of a steel for which s

250 MPa and E 5 200 GPa. It is free at its top A and fixed at its

base B. Using the allowable-stress method, determine the largest

allowable eccentricity e

, knowing that (a) e

5 0, (b) e

5 8 mm.

10.98 The compression member AB is made of a steel for which s

250 MPa and E 5 200 GPa. It is free at its top A and fixed at its

base B. Using the interaction method with an allowable bending

stress equal to 120 MPa and knowing that the eccentricities e

and

are equal, determine their largest allowable common value.

10.99 An eccentric load P 5 10 kips is applied at a point 0.8 in. from

the geometric axis of a 2-in.-diameter rod made of the aluminum

alloy 6061-T6. Using the interaction method and an allowable

stress in bending of 21 ksi, determine the largest allowable effec-

tive length L that can be used.

0.55 m

50 mm

75 mm

P  170 kN

Fig. P10.97 and P10.98

P  10 kips

0.8 in.

2 in. diameter

Fig. P10.99

10.100 Solve Prob. 10.99, assuming that the aluminum alloy used is 2014-

T6 and that the allowable stress in bending is 24 ksi.

10.101 A rectangular column is made of a grade of sawn wood that has

an adjusted allowable stress for compression parallel to the grain

5 8.3 MPa and an adjusted modulus of elasticity E 5 11.1 GPa.

Using the allowable-stress method, determine the largest allowable

effective length L that can be used.

10.102 Solve Prob. 10.101, assuming that P 5 105 kN.

10.103 An 11-kip vertical load P is applied at the midpoint of one edge

of the square cross section of the steel compression member AB,

which is free at its top A and fixed at its base B. Knowing that for

the grade of steel used s

5 36 ksi and E 5 29 3 10

psi. and using

the allowable-stress method, determine the smallest allowable

dimension d.

10.104 Solve Prob. 10.103, assuming that the vertical load P is applied at

the corner of the cross section.

P  85 kN

240 mm

180 mm

25 mm

Fig. P10.101

4.5 ft

P  11 kips

Fig. P10.103

bee80288_ch10_630-691.indd Page 681 11/1/10 2:39:12 PM user-f499bee80288_ch10_630-691.indd Page 681 11/1/10 2:39:12 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

682

Columns

10.105 A steel tube of 80-mm outer diameter is to carry a 93-kN load P

with an eccentricity of 20 mm. The tubes available for use are made

with wall thicknesses in increments of 3 mm from 6 mm to 15 mm.

Using the allowable-stress method, determine the lightest tube that

can be used. Assume E 5 200 GPa and s

5 250 MPa.

10.106 Solve Prob. 10.105, using the interaction method with P 5 165 kN,

e 5 15 mm, and an allowable stress in bending of 150 MPa.

10.107 A compression member of rectangular cross section has an effec-

tive length of 0.9 m and is made of the aluminum alloy 2014-T6

for which the allowable stress in bending is 160 MPa. Using the

interaction method, determine the smallest dimension d of the

cross section that can be used when e 5 10 mm.

10.108 Solve Prob. 10.107, assuming that e 5 5 mm.

10.109 An aluminum tube of 3-in. outside diameter is to carry a load of

10 kips having an eccentricity e 5 0.6 in. Knowing that the stock

of tubes available for use are made of alloy 2014-T6 and have wall

thicknesses in increments of

in. up to

in. determine the lightest

tube that can be used. Use the allowable-stress method.

10.110 Solve Prob. 10.109, using the interaction method of design with an

allowable stress in bending of 25 ksi.

10.111 A sawn lumber column of rectangular cross section has a 2.2-m

effective length and supports a 41-kN load as shown. The sizes

available for use have b equal to 90 mm, 140 mm, 190 mm, and

240 mm. The grade of wood has an adjusted allowable stress for

compression parallel to the grain s

5 8.1 MPa and an adjusted

modulus E 5 8.3 GPa. Using the allowable-stress method, deter-

mine the lightest section that can be used.

2.2 m

80-mm oute

diameter

e  20 mm

Fig. P10.105

P  144 kN

56 mm

Fig. P10.107

10.112 Solve Prob. 10.111, assuming that e 5 40 mm.

e  0.6 in.

3-in. outside

diameter

6 ft

P  10 kips

Fig. P10.109

41 kN

190 mm

e  80 mm

Fig. P10.111

bee80288_ch10_630-691.indd Page 682 11/1/10 2:39:21 PM user-f499bee80288_ch10_630-691.indd Page 682 11/1/10 2:39:21 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

683

Problems

10.113 A steel column having a 24-ft effective length is loaded eccentri-

cally as shown. Using the allowable-stress method, select the wide-

flange shape of 14-in. nominal depth that should be used. Use

5 36 ksi and E 5 29 3 10

psi.

10.114 Solve Prob. 10.113 using the interaction method, assuming that

5 50 ksi and the allowable stress in bending is 30 ksi.

10.115 A steel column of 7.2-m effective length is to support an 83-kN

eccentric load P at a point D, located on the x axis as shown. Using

the allowable-stress method, select the wide-flange shape of

250-mm nominal depth that should be used. Use E 5 200 GPa and

5 250 MPa.

P  120 kips

8 in.

Fig. P10.113

 70 mm

Fig. P10.115

125 mm

Fig. P10.116

10.116 A steel compression member of 5.8-m effective length is to support a

296-kN eccentric load P. Using the interaction method, select the

wide-flange shape of 200-mm nominal depth that should be used. Use

E 5 200 GPa, s

5 250 MPa, and s

all

5 150 MPa in bending.

bee80288_ch10_630-691.indd Page 683 11/1/10 2:39:30 PM user-f499bee80288_ch10_630-691.indd Page 683 11/1/10 2:39:30 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

684

REVIEW AND SUMMARY

This chapter was devoted to the design and analysis of columns, i.e.,

prismatic members supporting axial loads. In order to gain insight

into the behavior of columns, we first considered in Sec. 10.2 the

equilibrium of a simple model and found that for values of the load

P exceeding a certain value P

, called the critical load, two equilib-

rium positions of the model were possible: the original position with

zero transverse deflections and a second position involving deflec-

tions that could be quite large. This led us to conclude that the first

equilibrium position was unstable for P . P

, and stable for P , P

since in the latter case it was the only possible equilibrium

position.

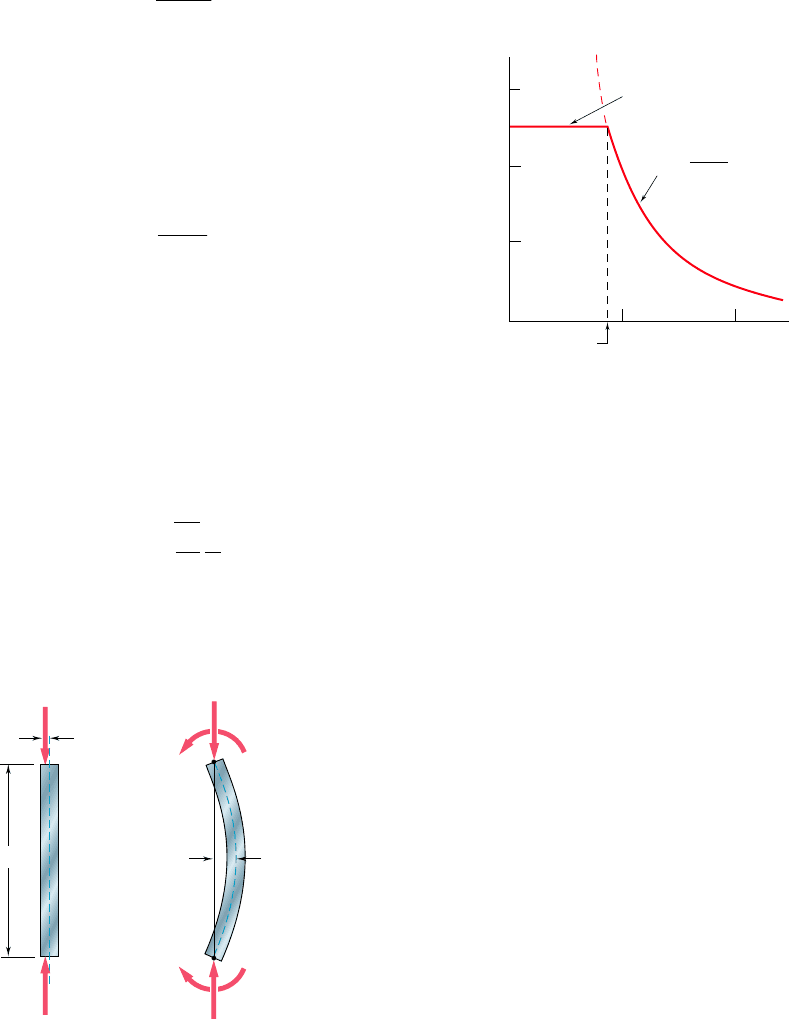
In Sec. 10.3, we considered a pin-ended column of length L and of

constant flexural rigidity EI subjected to an axial centric load P.

Assuming that the column had buckled (Fig. 10.36), we noted that

the bending moment at point Q was equal to 2Py and wrote

(10.4)

Critical load

Euler’s formula

[ x  0, y  0]

[ x  L, y  0]

(a)(b)

P P

Fig. 10.36

Solving this differential equation, subject to the boundary conditions

corresponding to a pin-ended column, we determined the smallest

load P for which buckling can take place. This load, known as the

critical load and denoted by P

, is given by Euler’s formula:

(10.11)

bee80288_ch10_630-691.indd Page 684 11/19/10 12:58:36 AM user-f499bee80288_ch10_630-691.indd Page 684 11/19/10 12:58:36 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10

Apago PDF Enhancer

685

where L is the length of the column. For this load or any larger load,

the equilibrium of the column is unstable and transverse deflections

will occur.

Denoting the cross-sectional area of the column by A and its

radius of gyration by r, we determined the critical stress s

corre-

sponding to the critical load P

(10.13)

The quantity Lyr is called the slenderness ratio and we plotted s

as a function of Lyr (Fig. 10.37). Since our analysis was based on

stresses remaining below the yield strength of the material, we noted

that the column would fail by yielding when s

. s

In Sec. 10.4, we discussed the critical load of columns with

various end conditions and wrote

(10.119)

where L

is the effective length of the column, i.e., the length of

an equivalent pin-ended column. The effective lengths of several

columns with various end conditions were calculated and shown in

Fig. 10.17 on page 642.

In Sec. 10.5, we considered columns supporting an eccentric axial

load. For a pin-ended column subjected to a load P applied with an

eccentricity e, we replaced the load by a centric axial load and a

couple of moment M

5 Pe (Figs. 10.38 and 10.39) and derived the

following expression for the maximum transverse deflection:

max

5 e

sec

2 1

(10.28)

100

0 100

200

250

300

(MPa)

 250 MPa

E  200 GPa

(L/r)









Fig. 10.37

Effective length

Review and Summary

Eccentric axial load. Secant formula.

Fig. 10.38

 Pe

max

Fig. 10.39

Slenderness ratio

bee80288_ch10_630-691.indd Page 685 11/1/10 2:39:43 PM user-f499bee80288_ch10_630-691.indd Page 685 11/1/10 2:39:43 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch

Apago PDF Enhancer

686

Columns

We then determined the maximum stress in the column, and from the

expression obtained for that stress, we derived the secant formula:

max

1 1

sec

(10.36)

This equation can be solved for the force per unit area, PyA, that

causes a specified maximum stress s

max

in a pin-ended column or

any other column of effective slenderness ratio L

yr.

In the first part of the chapter we considered each column as a

straight homogeneous prism. Since imperfections exist in all real col-

umns, the design of real columns is done by using empirical formulas

based on laboratory tests and set forth in specifications and codes

issued by professional organizations. In Sec. 10.6, we discussed the

design of centrically loaded columns made of steel, aluminum, or

wood. For each material, the design of the column was based on

formulas expressing the allowable stress as a function of the slender-

ness ratio Lyr of the column. For structural steel, we also discussed

the alternative method of Load and Resistance Factor Design.

In the last section of the chapter [Sec. 10.7], we studied two methods

used for the design of columns under an eccentric load. The first

method was the allowable-stress method, a conservative method in

which it is assumed that the allowable stress is the same as if the

column were centrically loaded. The allowble-stress method requires

that the following inequality be satisfied:

# s

all

(10.53)

The second method was the interaction method, a method used in

most modern specifications. In this method the allowable stress for

a centrically loaded column is used for the portion of the total stress

due to the axial load and the allowable stress in bending for the stress

due to bending. Thus, the inequality to be satisfied is

all

centric

all

bendin

# 1

(10.55)

Eccentrically loaded columns

Allowable-stress method

Interaction method

Design of real columns

Centrically loaded columns

bee80288_ch10_630-691.indd Page 686 11/1/10 2:39:45 PM user-f499bee80288_ch10_630-691.indd Page 686 11/1/10 2:39:45 PM user-f499/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch10/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch