Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.

Apago PDF Enhancer
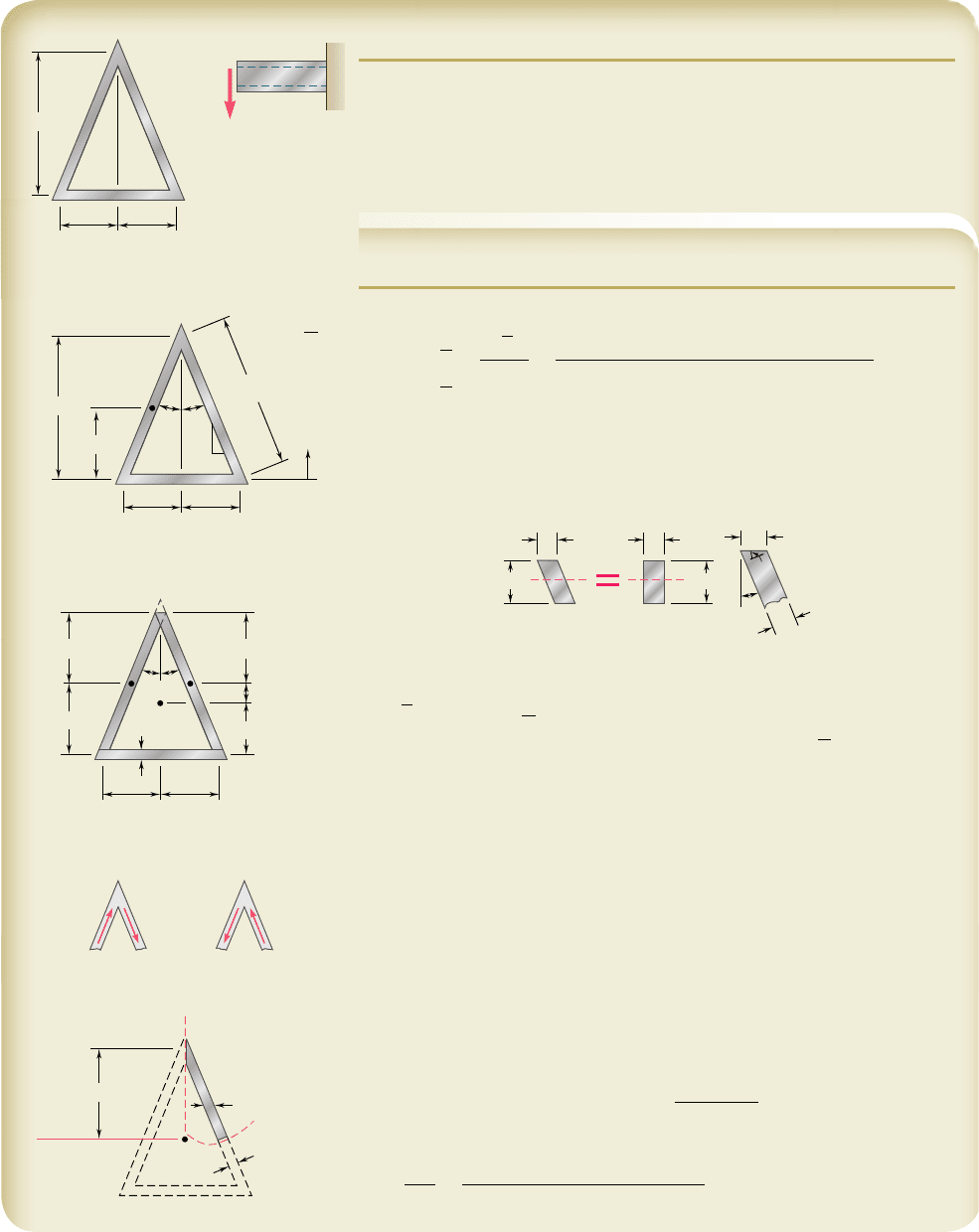
SAMPLE PROBLEM 6.5
The thin-walled extruded beam shown is made of aluminum and has a uniform
3-mm wall thickness. Knowing that the shear in the beam is 5 kN, determine
(a) the shearing stress at point A, (b) the maximum shearing stress in the beam.
Note: The dimensions given are to lines midway between the outer and inner
surfaces of the beam.
SOLUTION
Centroid. We note that AB 5 AD 5 65 mm.
Y 5
o
y
A
o
A
5
23165 mm213 mm2130 mm2
4
23165 mm213 mm241 150 mm213 mm2
Y 5 21
.
67 mm
Centroidal Moment of Inertia. Each side of the thin-walled beam can
be considered as a parallelogram, and we recall that for the case shown
I
nn
5 bh
3
y12 where b is measured parallel to the axis nn.
b 5 13 mm2
y
cos b 5 13 mm2
y
112
y
1325 3.25 mm
I 5 o 1
I 1 Ad
2
25 23
1
12
13.25 mm2160 mm2
3
1 13.25 mm2160 mm218.33 mm2
2
41 3
1
12
150 mm213 mm2
3
1 150 mm213 mm2121.67 mm2
2
4
I 5 214
.
6 3 10
3
mm
4
I 5 0
.
2146 3 10
26
m
4
a. Shearing Stress at A. If a shearing stress t
A
occurs at A, the shear
flow will be q
A
5 t
A
t and must be directed in one of the two ways shown.
But the cross section and the loading are symmetric about a vertical line
through A, and thus the shear flow must also be symmetric. Since neither
of the possible shear flows is symmetric, we conclude that t
A
5 0b
b. Maximum Shearing Stress. Since the wall thickness is constant,
the maximum shearing stress occurs at the neutral axis, where Q is maxi-
mum. Since we know that the shearing stress at A is zero, we cut the section
along the dashed line shown and isolate the shaded portion of the beam. In
order to obtain the largest shearing stress, the cut at the neutral axis is made
perpendicular to the sides, and is of length t 5 3 mm.
Q 5 313.25 mm2138.33 mm24 a
38.33 m
m
2
b5 2387 mm
3
Q 5 2.387 3 10
26
m
3
t
E
5
V
Q
It
5
15 kN212.387 3 10
26
m
3
2
10.2146 3 10
26
m
4
210.003 m2
t
m
a
x
5 t
E
5 18.54 MPab
D
B
A
60 mm
65 mm
cos
12
13
⫽
13
12
5
y


30 mm
25 mm 25 mm
hh
bb
nn nn
3 mm


3.25 mm
D
C
B
A
30 mm
21.67 mm
3 mm
8.33 mm


30 mm
30 mm
25 mm 25 mm
q
A
q
A
q
A
q
A
OR
b ⫽ 3.25 mm
t ⫽ 3 mm
C
A
E
Neutral axis
38.33 mm
5 kN
D
B
A
60 mm
25 mm 25 mm
407
bee80288_ch06_380-435.indd Page 407 10/29/10 7:45:55 PM user-f499bee80288_ch06_380-435.indd Page 407 10/29/10 7:45:55 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
PROBLEMS
408
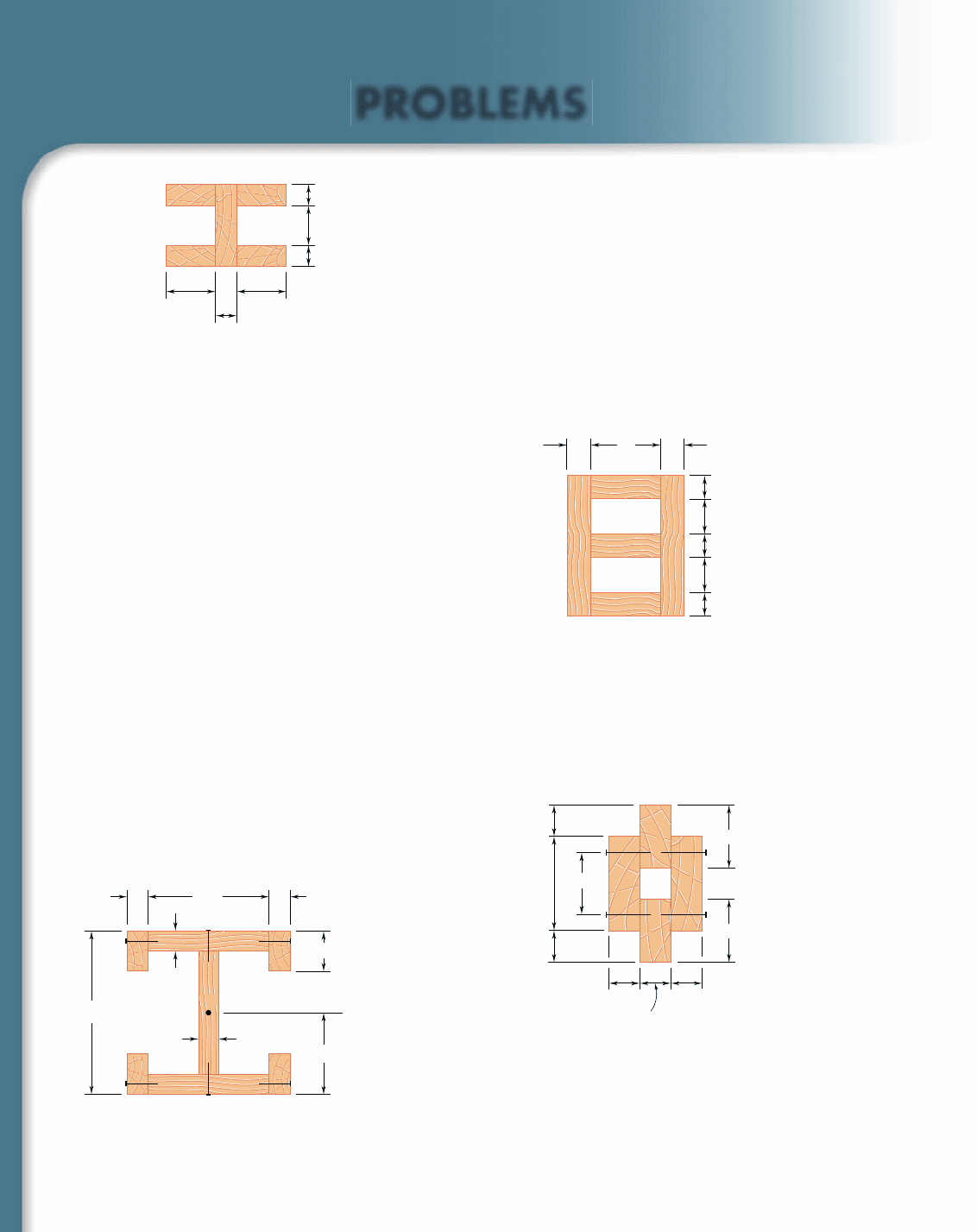
6.32 The built-up timber beam is subjected to a 1500-lb vertical shear.
Knowing that the longitudinal spacing of the nails is s 5 2.5 in.
and that each nail is 3.5 in. long, determine the shearing force in
each nail.
6.29 The built-up beam shown is made by gluing together five planks.
Knowing that in the glued joints the average allowable shearing
stress is 350 kPa, determine the largest permissible vertical shear
in the beam.
6.30 For the beam of Prob. 6.29, determine the largest permissible hori-
zontal shear.
6.31 Several wooden planks are glued together to form the box beam
shown. Knowing that the beam is subjected to a vertical shear of
3 kN, determine the average shearing stress in the glued joint
(a) at A, (b) at B.
40 mm
80 mm
40 mm
40 mm
100 mm 100 mm
Fig. P6.29
Fig. P6.31
20 60 20
20
30
20
30
20
Dimensions in mm
A
B
4 in.
4 in.
2 in. 2 in.
2 in.
2 in.
6 in. 4 in.
2 in.
Fig. P6.32
6.33 The built-up wooden beam shown is subjected to a vertical shear
of 8 kN. Knowing that the nails are spaced longitudinally every
60 mm at A and every 25 mm at B, determine the shearing force
in the nails (a) at A, (b) at B. (Given: I
x
5 1.504 3 10
9
mm
4
.)
Fig. P6.33
300
100
200
400
50
50
50
50
B
B
A
x
AA
A
C
Dimensions in mm
bee80288_ch06_380-435.indd Page 408 10/28/10 8:01:33 PM user-f499bee80288_ch06_380-435.indd Page 408 10/28/10 8:01:33 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
409
Problems
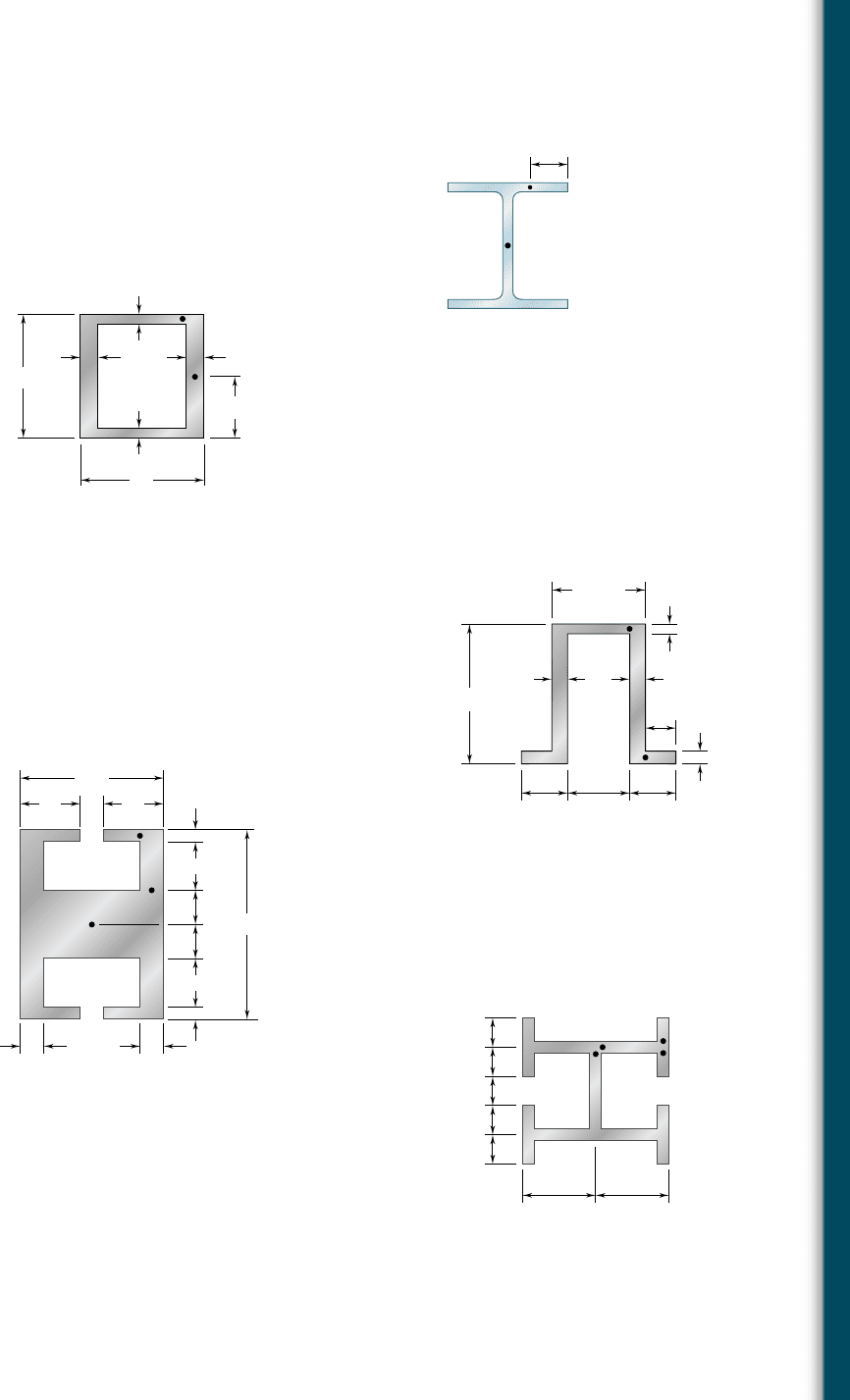
6.34 Knowing that a vertical shear V of 50 kips is exerted on a W14 3
82 rolled-steel beam, determine the shearing stress (a) at point a,
(b) at the centroid C.
6.35 An extruded aluminum beam has the cross section shown. Know-
ing that the vertical shear in the beam is 150 kN, determine the
shearing stress at (a) point a, (b) point b.
Fig. P6.34
a
C
4.15 in.
Fig. P6.35
b
1212
40
80
80
Dimensions in mm
6
6
a
6.36 Knowing that a given vertical shear V causes a maximum shearing
stress of 75 MPa in the hat-shaped extrusion shown, determine the
corresponding shearing stress at (a) point a, (b) point b.
6.37 Knowing that a given vertical shear V causes a maximum shearing
stress of 75 MPa in an extruded beam having the cross section shown,
determine the shearing stress at the three points indicated.
Fig. P6.36
60 mm
20 mm 28 mm 20 mm
4 mm
4 mm
14 mm
6 mm 6 mm
b
a
40 mm
Fig. P6.37
40
30
30
40
10
10
160
120
50 50
20 20
c
b
a
Dimensions in mm
Fig. P6.38
1.5 in.
d
c
a
b
0.6 in.
0.6 in.
0.6 in.
0.6 in.
0.6 in.
1.5 in.
6.38 An extruded beam has the cross section shown and a uniform wall
thickness of 0.20 in. Knowing that a given vertical shear V causes
a maximum shearing stress t
5 9 ksi, determine the shearing stress
at the four points indicated.
6.39 Solve Prob. 6.38 assuming that the beam is subjected to a horizon-
tal shear V.
bee80288_ch06_380-435.indd Page 409 10/28/10 8:01:42 PM user-f499bee80288_ch06_380-435.indd Page 409 10/28/10 8:01:42 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
410
Shearing Stresses in Beams
and Thin-Walled Members
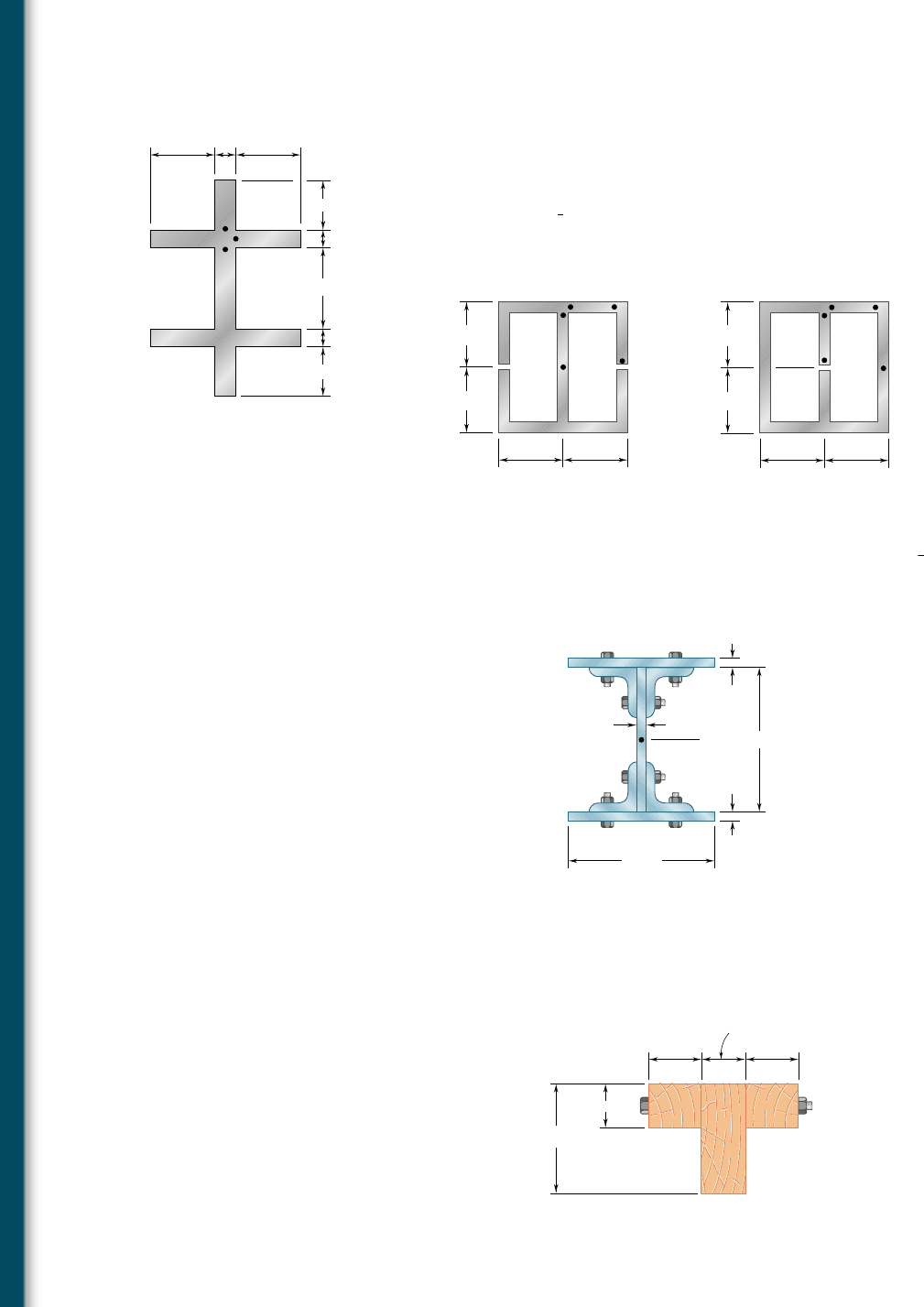
6.40 Knowing that a given vertical shear V causes a maximum shearing
stress of 50 MPa in a thin-walled member having the cross section
shown, determine the corresponding shearing stress at (a) point a,
(b) point b, (c) point c.
6.41 and 6.42 The extruded aluminum beam has a uniform wall
thickness of
1
8
in. Knowing that the vertical shear in the beam is
2 kips, determine the corresponding shearing stress at each of the
five points indicated.
6.43 Three 1 3 18-in. steel plates are bolted to four L6 3 6 3 1 angles to
form a beam with the cross section shown. The bolts have a
7
8
-in.
diameter and are spaced longitudinally every 5 in. Knowing that the
allowable average shearing stress in the bolts is 12 ksi, determine the
largest permissible vertical shear in the beam. (Given: I
x
5 6123 in
4
.)
Fig. P6.40
40 mm
30 mm
50 mm
30 mm
10 mm
10 mm
12 mm40 mm
b
c
a
1.25 in.
1.25 in.
1.25 in. 1.25 in.
b
c
a
e
d
Fig. P6.42
1.25 in.
1.25 in.
1.25 in. 1.25 in.
b
c
a
e
d
Fig. P6.41
Fig. P6.43
C
1 in.
1 in.
1 in.
18 in.
18 in.
x
Fig. P6.44
125 mm 125 mm
100 mm
100 mm
250 mm
6.44 Three planks are connected as shown by bolts of 14-mm diameter
spaced every 150 mm along the longitudinal axis of the beam. For
a vertical shear of 10 kN, determine the average shearing stress in
the bolts.
bee80288_ch06_380-435.indd Page 410 10/28/10 8:01:51 PM user-f499bee80288_ch06_380-435.indd Page 410 10/28/10 8:01:51 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
411
Problems
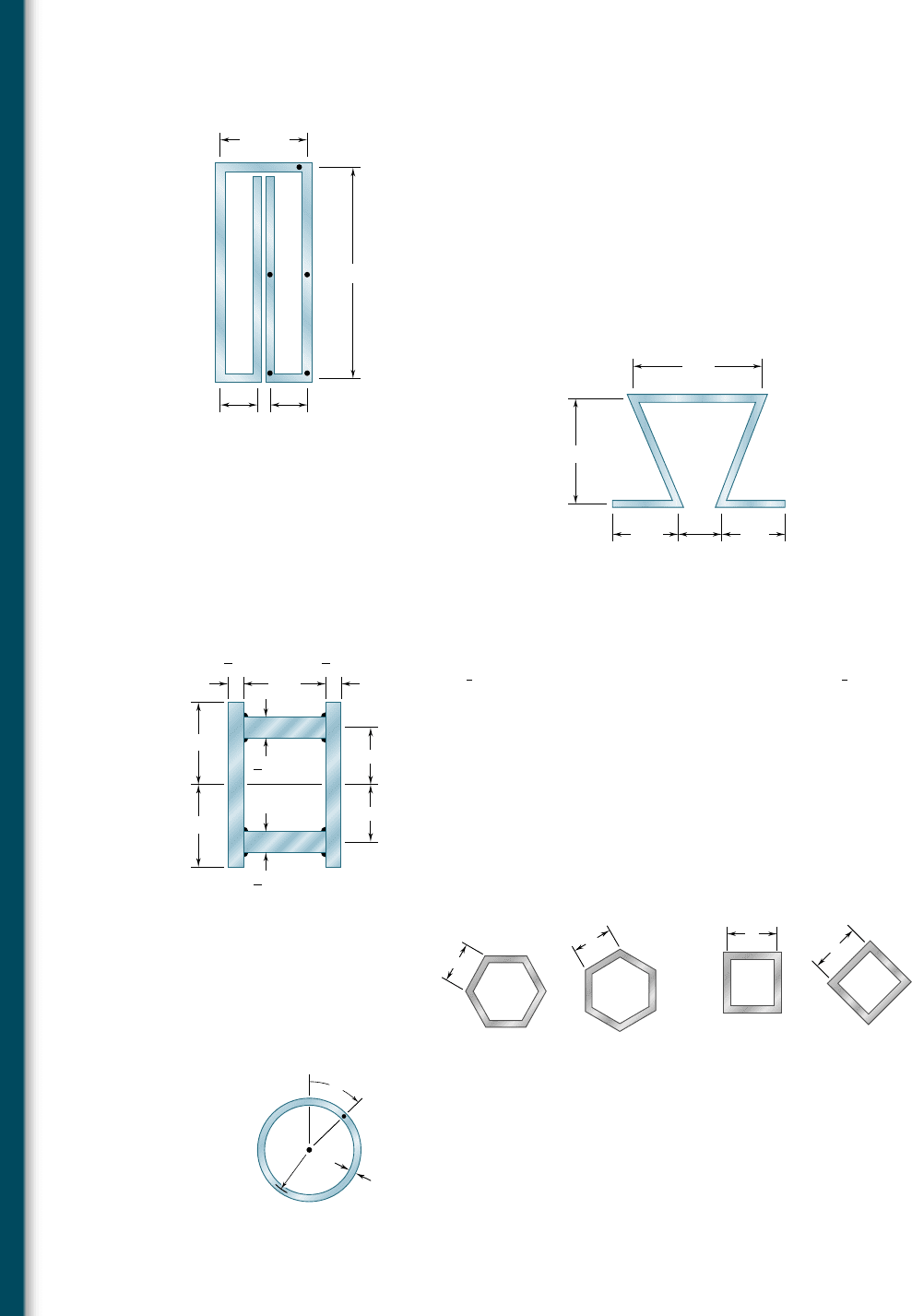
6.45 A beam consists of three planks connected as shown by steel bolts
with a longitudinal spacing of 225 mm. Knowing that the shear in
the beam is vertical and equal to 6 kN and that the allowable aver-
age shearing stress in each bolt is 60 MPa, determine the smallest
permissible bolt diameter that can be used.
Fig. P6.45
100 mm
100 mm
50 mm100 mm50 mm
25 mm
25 mm
6.46 A beam consists of five planks of 1.5 3 6-in. cross section con-
nected by steel bolts with a longitudinal spacing of 9 in. Knowing
that the shear in the beam is vertical and equal to 2000 lb and that
the allowable average shearing stress in each bolt is 7500 psi, deter-
mine the smallest permissible bolt diameter that can be used.
6.47 A plate of
1
4
-in. thickness is corrugated as shown and then used as
a beam. For a vertical shear of 1.2 kips, determine (a) the maxi-
mum shearing stress in the section, (b) the shearing stress at point B.
Also sketch the shear flow in the cross section.
Fig. P6.46
6 in.
1 in.
1 in.
Fig. P6.47
1.6 in.
2 in. 2 in.
1.2 in. 1.2 in.
AB
D
EF
6.48 A plate of 4-mm thickness is bent as shown and then used as a
beam. For a vertical shear of 12 kN, determine (a) the shearing
stress at point A, (b) the maximum shearing stress in the beam.
Also sketch the shear flow in the cross section.
Fig. P6.48
Dimensions in mm
25
A
20 25
48
20
50
bee80288_ch06_380-435.indd Page 411 11/13/10 12:25:51 AM user-f499bee80288_ch06_380-435.indd Page 411 11/13/10 12:25:51 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch06/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch06
Apago PDF Enhancer
412
Shearing Stresses in Beams
and Thin-Walled Members
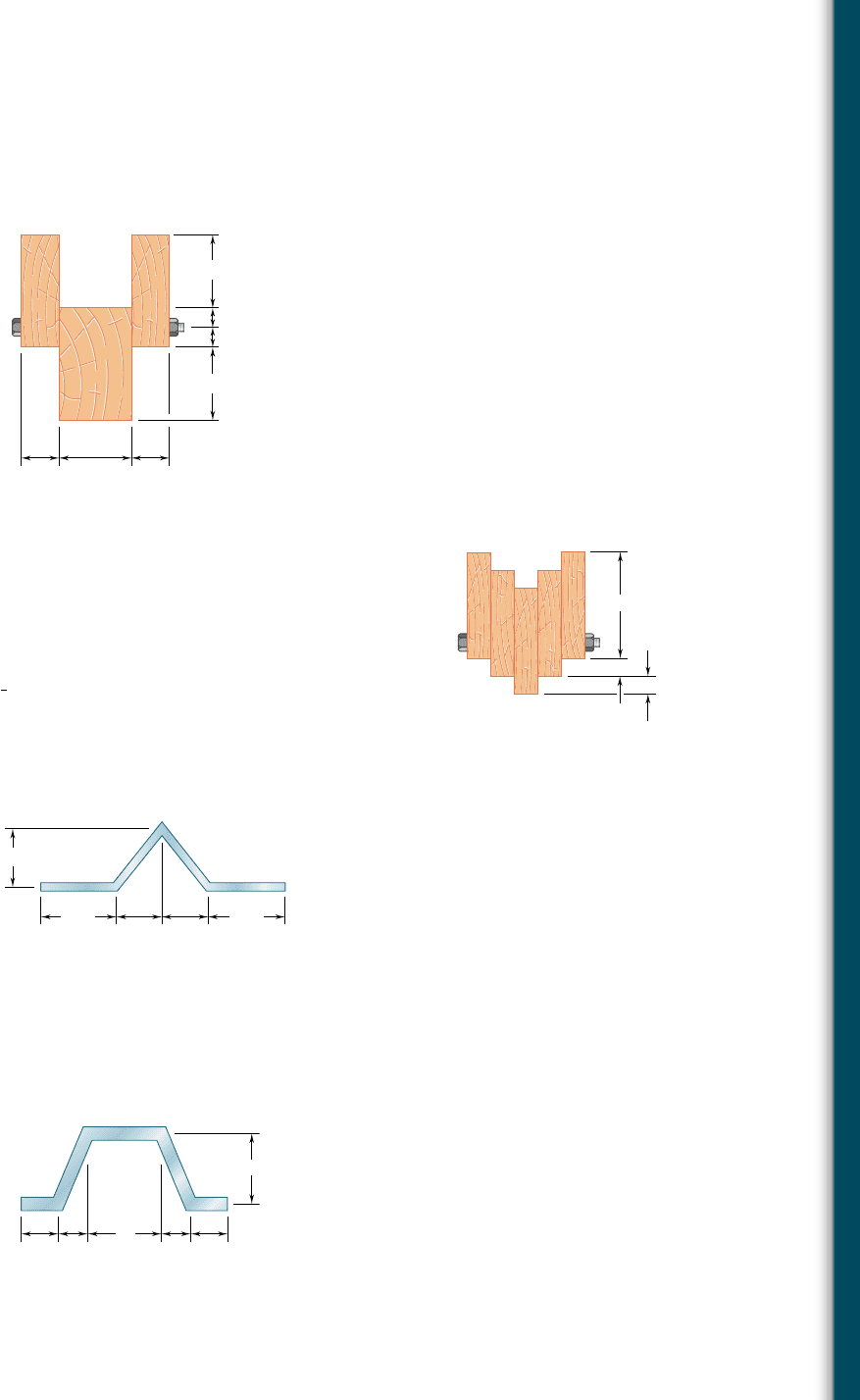
6.49 A plate of 2-mm thickness is bent as shown and then used as a
beam. For a vertical shear of 5 kN, determine the shearing stress
at the five points indicated and sketch the shear flow in the cross
section.
6.50 A plate of thickness t is bent as shown and then used as a beam.
For a vertical shear of 600 lb, determine (a) the thickness t for
which the maximum shearing stress is 300 psi, (b) the correspond-
ing shearing stress at point E. Also sketch the shear flow in the
cross section.
d
a
e
bc
50 mm
10 mm 10 mm
22 mm
Fig. P6.49
6.51 The design of a beam calls for connecting two vertical rectangular
3
8
3 4-in. plates by welding them to two horizontal
1
2
3 2-in. plates
as shown. For a vertical shear V, determine the dimension a for
which the shear flow through the welded surfaces is maximum.
6.52 and 6.53 An extruded beam has a uniform wall thickness t.
Denoting by V the vertical shear and by A the cross-sectional area
of the beam, express the maximum shearing stress as t
max
5 k(VyA)
and determine the constant k for each of the two orientations
shown.
Fig. P6.50
4.8 in.
6 in.
3 in. 3 in.
2 in.
B
G
E
D
FA
2 in.
2 in.
2 in.
a
a
in.
3
8
in.
1
2
in.
1
2
in.
3
8
Fig. P6.51
Fig. P6.52
(a)
a
a
(b)
Fig. P6.53
a
a
(a)(b)
6.54 (a) Determine the shearing stress at point P of a thin-walled pipe
of the cross section shown caused by a vertical shear V. (b) Show
that the maximum shearing stress occurs for u 5 908 and is equal
to 2VyA, where A is the cross-sectional area of the pipe.
Fig. P6.54
C
r
m
t
P
bee80288_ch06_380-435.indd Page 412 10/28/10 8:02:07 PM user-f499bee80288_ch06_380-435.indd Page 412 10/28/10 8:02:07 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer
413
Problems
6.55 For a beam made of two or more materials with different moduli
of elasticity, show that Eq. (6.6)
t
ave
5
VQ
I
t
remains valid provided that both Q and I are computed by using the
transformed section of the beam (see Sec. 4.6) and provided further
that t is the actual width of the beam where t
ave
is computed.
6.56 and 6.57 A steel bar and an aluminum bar are bonded together
as shown to form a composite beam. Knowing that the vertical
shear in the beam is 4 kips and that the modulus of elasticity is
29 3 10
6
psi for the steel and 10.6 3 10
6
psi for the aluminum,
determine (a) the average stress at the bonded surface, (b) the
maximum shearing stress in the beam. (Hint: Use the method indi-
cated in Prob. 6.55.)
6.58 and 6.59 A composite beam is made by attaching the timber
and steel portions shown with bolts of 12-mm diameter spaced
longitudinally every 200 mm. The modulus of elasticity is 10 GPa
for the wood and 200 GPa for the steel. For a vertical shear of 4 kN,
determine (a) the average shearing stress in the bolts, (b) the shear-
ing stress at the center of the cross section. (Hint: Use the method
indicated in Prob. 6.55.)
Fig. P6.56
2 in.
1 in.
1.5 in.
Steel
Aluminum
Fig. P6.57
2 in.
1 in.
1.5 in.
Aluminum
Steel
Fig. P6.58
150 mm
12 mm
250 mm
12 mm
140 mm 6 mm6 mm
90 mm
90 mm
84 mm
Fig. P6.59
bee80288_ch06_380-435.indd Page 413 10/28/10 8:02:19 PM user-f499bee80288_ch06_380-435.indd Page 413 10/28/10 8:02:19 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer
6.60 Consider the cantilever beam AB discussed in Sec. 6.8 and the
portion ACKJ of the beam that is located to the left of the trans-
verse section CC9 and above the horizontal plane JK, where K is
a point at a distance y , y
Y
above the neutral axis (Fig. P6.60).
(a) Recalling that s
x
5 s
Y
between C and E and s
x
5 (s
Y
yy
Y
)y
between E and K, show that the magnitude of the horizontal
shearing force H exerted on the lower face of the portion of beam
ACKJ is
H 5
1
2
bs
Y
a2c 2 y
Y
2
y
2
y
Y
b
(b) Observing that the shearing stress at K is
t
xy
5 lim
¢Ay0
¢H
¢A
5 lim
¢xy0
1
b
¢H
¢x
5
1
b
0H
0x
and recalling that y
Y
is a function of x defined by Eq. (6.14), derive
Eq. (6.15).
A
J
x
CE
K
B
Plastic
Neutral axis
P
E'
C'
y
y
Y
Fig. P6.60
*6.9 UNSYMMETRIC LOADING OF THIN-WALLED
MEMBERS; SHEAR CENTER
Our analysis of the effects of transverse loadings in Chap. 5 and in
the preceding sections of this chapter was limited to members pos-
sessing a vertical plane of symmetry and to loads applied in that
plane. The members were observed to bend in the plane of loading
(Fig. 6.39) and, in any given cross section, the bending couple M
and the shear V (Fig. 6.40) were found to result in normal and shear-
ing stresses defined, respectively, by the formulas
s
x
52
M
y
I
(4.16)
and
t
ave
5
V
Q
It
(6.6)
In this section, the effects of transverse loadings on thin-walled
members that do not possess a vertical plane of symmetry will be
C
x
P
Fig. 6.39 Channel beam.
M
V
N.A.
C'
(V P, M Px)
Fig. 6.40 Loaded in vertical
plane of symmetry.
414
Shearing Stresses in Beams
and Thin-Walled Members
bee80288_ch06_380-435.indd Page 414 10/28/10 8:02:27 PM user-f499bee80288_ch06_380-435.indd Page 414 10/28/10 8:02:27 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
Apago PDF Enhancer
415
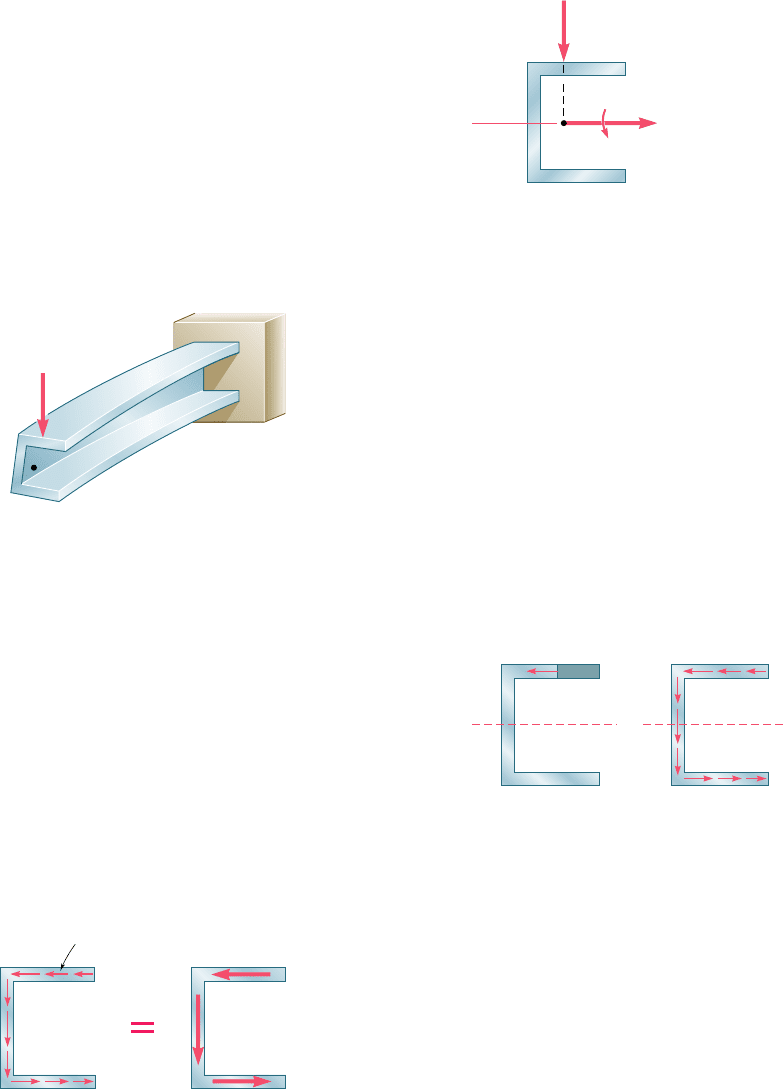
examined. Let us assume, for example, that the channel member of
Fig. 6.39 has been rotated through 908 and that the line of action of
P still passes through the centroid of the end section. The couple vec-
tor M representing the bending moment in a given cross section is
still directed along a principal axis of the section (Fig. 6.41), and the
neutral axis will coincide with that axis (cf. Sec. 4.13). Equation (4.16),
therefore, is applicable and can be used to compute the normal stresses
in the section. However, Eq. (6.6) cannot be used to determine the
shearing stresses in the section, since this equation was derived for a
member possessing a vertical plane of symmetry (cf. Sec. 6.7). Actually,
the member will be observed to bend and twist under the applied load
(Fig. 6.42), and the resulting distribution of shearing stresses will be
quite different from that defined by Eq. (6.6).
M
N.A.
C'
(V P, M Px)
V
Fig. 6.41 Load
perpendicular to vertical
plane of symmetry.
6.9 Unsymmetric Loading of Thin-Walled
Members; Shear Center
C
P
Fig. 6.42 Deformation of channel
beam when not loaded in vertical
plane of symmetry.
N.A.
DE
AB
N.A.
DE
AB
(a) Shear stress (b) Shear flow q
Fig. 6.43 Stresses applied to cross section
as a result of load shown in Fig. 6.42.
DE
AB
dF q ds
F
V
F'
DE
AB
(a) Shear flow q (b) Resultant forces
on elements
Fig. 6.44
The following question now arises: Is it possible to apply the
vertical load P in such a way that the channel member of Fig. 6.42
will bend without twisting and, if so, where should the load P be
applied? If the member bends without twisting, then the shearing
stress at any point of a given cross section can be obtained from
Eq. (6.6), where Q is the first moment of the shaded area with
respect to the neutral axis (Fig. 6.43a), and the distribution of stresses
will look as shown in Fig. 6.43b, with t 5 0 at both A and E. We
note that the shearing force exerted on a small element of cross-
sectional area dA 5 t ds is dF 5 t dA 5 tt ds, or dF 5 q ds (Fig.6.44a),
bee80288_ch06_380-435.indd Page 415 10/28/10 8:02:35 PM user-f499bee80288_ch06_380-435.indd Page 415 10/28/10 8:02:35 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer
416
Shearing Stresses in Beams
and Thin-Walled Members
P
P
y
P
z
(a)(b)
e
OO
Fig. 6.47 Beam with oblique load.
where q is the shear flow q 5 tt 5 VQyI at the point considered.
The resultant of the shearing forces exerted on the elements of the
upper flange AB of the channel is found to be a horizontal force F
(Fig. 6.44b) of magnitude
F 5
#
B
A
q ds (6.17)
Because of the symmetry of the channel section about its neutral
axis, the resultant of the shearing forces exerted on the lower flange
DE is a force F9 of the same magnitude as F but of opposite sense.
We conclude that the resultant of the shearing forces exerted on the
web BD must be equal to the vertical shear V in the section:
V 5
#
D
B
q ds
(6.18)
We now observe that the forces F and F9 form a couple of
moment Fh, where h is the distance between the center lines of the
flanges AB and DE (Fig. 6.45a). This couple can be eliminated if
the vertical shear V is moved to the left through a distance e such
that the moment of V about B is equal to Fh (Fig. 6.45b). We write
Ve 5 Fh or
e 5
F
h
V
(6.19)
and conclude that, when the force P is applied at a distance e to the
left of the center line of the web BD, the member bends in a vertical
plane without twisting (Fig. 6.46).
The point O where the line of action of P intersects the axis of
symmetry of the end section is called the shear center of that section.
We note that, in the case of an oblique load P (Fig. 6.47a), the
member will also be free of any twist if the load P is applied at the
shear center of the section. Indeed, the load P can then be resolved
into two components P
z
and P
y
(Fig. 6.47b) corresponding respec-
tively to the loading conditions of Figs. 6.39 and 6.46, neither of
which causes the member to twist.
F
V
V
F'
D
E
A
e
h
B
D
E
A
B
(a) Resultant forces
on elements
(b) Placement of V to
eliminate twisting
Fig. 6.45
e
O
P
Fig. 6.46 Placement of load to
eliminate twisting.
bee80288_ch06_380-435.indd Page 416 10/28/10 8:02:39 PM user-f499bee80288_ch06_380-435.indd Page 416 10/28/10 8:02:39 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles
