Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

387

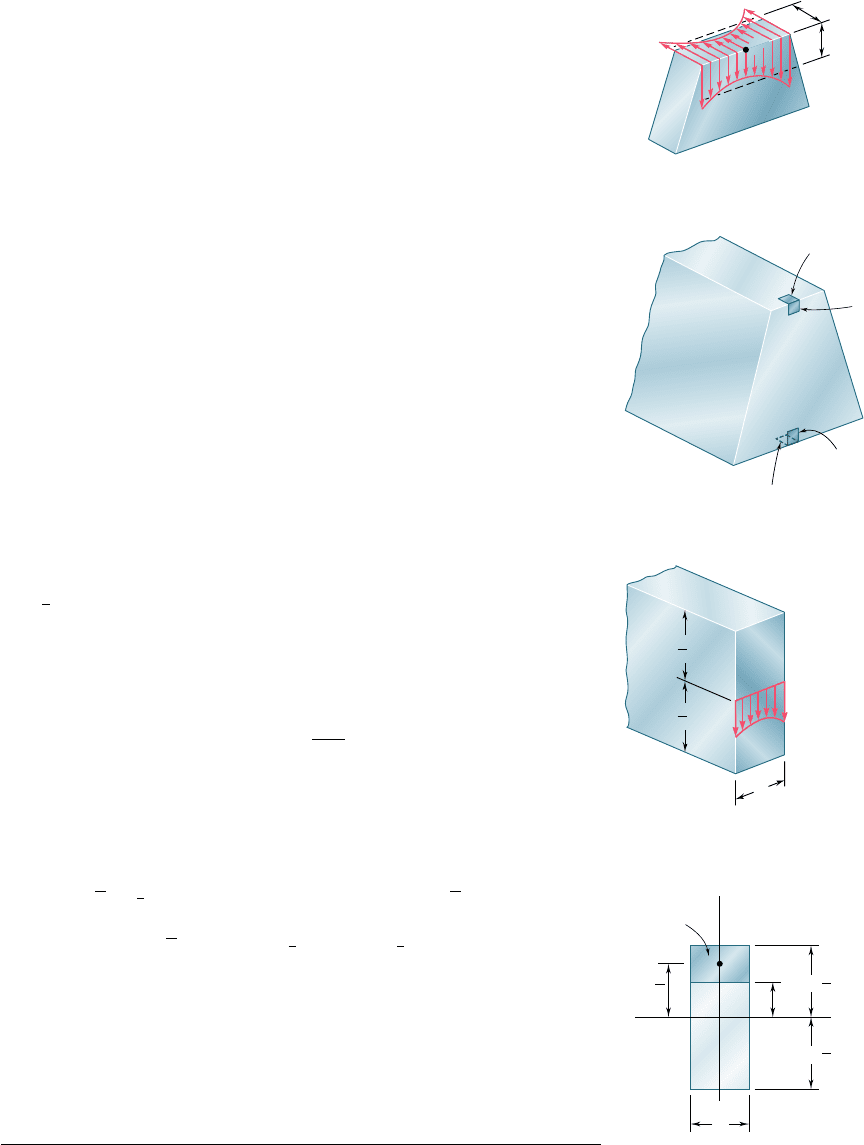
We note that, since the shearing stresses t

and t

exerted respec-

tively on a transverse and a horizontal plane through D9 are equal,

the expression obtained also represents the average value of t

along

the line D9

(Fig. 6.11).

We observe that t

5 0 on the upper and lower faces of the

beam, since no forces are exerted on these faces. It follows that

5 0 along the upper and lower edges of the transverse section

(Fig. 6.12). We also note that, while Q is maximum for y 5 0 (see

Sec. 6.2), we cannot conclude that t

ave

will be maximum along the

neutral axis, since t

ave

depends upon the width t of the section as

well as upon Q.

As long as the width of the beam cross section remains small

compared to its depth, the shearing stress varies only slightly along

the line D9

(Fig. 6.11) and Eq. (6.6) can be used to compute t

at any point along D9

. Actually, t

is larger at points D9

and D9

than at D9, but the theory of elasticity shows† that, for a beam of

rectangular section of width b and depth h, and as long as b # hy4,

the value of the shearing stress at points C

and C

(Fig. 6.13) does not

exceed by more than 0.8% the average value of the stress computed

along the neutral axis.‡

6.4 SHEARING STRESSES T

IN COMMON

TYPES OF BEAMS

We saw in the preceding section that, for a narrow rectangular beam,

i.e., for a beam of rectangular section of width b and depth h with

b #

h, the variation of the shearing stress t

across the width of the

beam is less than 0.8% of t

ave

. We can, therefore, use Eq. (6.6) in

practical applications to determine the shearing stress at any point of

the cross section of a narrow rectangular beam and write

(6.7)

where t is equal to the width b of the beam, and where Q is the

first moment with respect to the neutral axis of the shaded area A

(Fig. 6.14).

Observing that the distance from the neutral axis to the centroid

C9 of A is

1c 1 y2, and recalling that Q 5 A y, we write

Q 5 A

y 5 b1c 2 y2

1c 1 y25

b1c

2 y

2 (6.8)

†See S. P. Timoshenko and J. N. Goodier, Theory of Elasticity, McGraw-Hill, New York,

3d ed., 1970, sec. 124.

‡On the other hand, for large values of byh, the value t

max

of the stress at C

and C

may

be many times larger then the average value t

ave

computed along the neutral axis, as we

may see from the following table:

b/h 0.25 0.5 1 2 4 6 10 20 50

maxy

ave

1.008 1.033 1.126 1.396 1.988 2.582 3.770 6.740 15.65

miny

ave

0.996 0.983 0.940 0.856 0.805 0.800 0.800 0.800 0.800



ave



ave



D''

C''

D''

Fig. 6.11 Beam segment.



 0



 0



 0



 0

Fig. 6.12 Beam cross section.

6.4 Shearing Stresses t

in Common

Types of Beams



N.A.

Fig. 6.13 Rectangular

beam cross section.

hc 

c 

Fig. 6.14 Beam cross

section.

bee80288_ch06_380-435.indd Page 387 11/13/10 12:25:18 AM user-f499bee80288_ch06_380-435.indd Page 387 11/13/10 12:25:18 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch06/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch06

Apago PDF Enhancer

388

Shearing Stresses in Beams

and Thin-Walled Members

Recalling, on the other hand, that I 5 bh

12 5

, we have

2 y

or, noting that the cross-sectional area of the beam is A 5 2bc,

a1 2

b (6.9)

Equation (6.9) shows that the distribution of shearing stresses

in a transverse section of a rectangular beam is parabolic (Fig. 6.15).

As we have already observed in the preceding section, the shearing

stresses are zero at the top and bottom of the cross section (y 5 6c).

Making y 5 0 in Eq. (6.9), we obtain the value of the maximum

shearing stress in a given section of a narrow rectangular beam:

max

(6.10)

The relation obtained shows that the maximum value of the shearing

stress in a beam of rectangular cross section is 50% larger than the

value V/A that would be obtained by wrongly assuming a uniform

stress distribution across the entire cross section.

In the case of an American standard beam (S-beam) or a wide-

flange beam (W-beam), Eq. (6.6) can be used to determine the aver-

age value of the shearing stress t

over a section aa9 or bb9 of the

transverse cross section of the beam (Figs. 6.16a and b). We write

ave

(6.6)

where V is the vertical shear, t the width of the section at the eleva-

tion considered, Q the first moment of the shaded area with respect

to the neutral axis cc9, and I the moment of inertia of the entire

cross-sectional area about cc9. Plotting t

ave

against the vertical dis-

tance y, we obtain the curve shown in Fig. 6.16c. We note the

discontinuities existing in this curve, which reflect the difference

between the values of t corresponding respectively to the flanges

ABGD and A9B9G9D9 and to the web EFF9E9.

In the case of the web, the shearing stress t

varies only very

slightly across the section bb9, and can be assumed equal to its average



max

c

c

Fig. 6.15 Shear stress distribution on

transverse section of rectangular beam.

EFG

cc' c'

D' E' F' G'

A' B'

(a)

E' F'

(b)(c)

ave



Fig. 6.16 Shear stress distribution on transverse section of

wide-flange beam.

bee80288_ch06_380-435.indd Page 388 11/13/10 12:25:25 AM user-f499bee80288_ch06_380-435.indd Page 388 11/13/10 12:25:25 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch06/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch06

Apago PDF Enhancer

389

value t

ave

. This is not true, however, for the flanges. For example,

considering the horizontal line DEFG, we note that t

is zero between

D and E and between F and G, since these two segments are part of

the free surface of the beam. On the other hand the value of t

between E and F can be obtained by making t 5 EF in Eq. (6.6). In

practice, one usually assumes that the entire shear load is carried by

the web, and that a good approximation of the maximum value of the

shearing stress in the cross section can be obtained by dividing V by

the cross-sectional area of the web.

max

web

(6.11)

We should note, however, that while the vertical component

of the shearing stress in the flanges can be neglected, its hori-

zontal component t

has a significant value that will be determined

in Sec. 6.7.

EXAMPLE 6.02

Knowing that the allowable shearing stress for the timber beam of Sample

Prob. 5.7 is t

all

5 0.250 ksi, check that the design obtained in that sample

problem is acceptable from the point of view of the shearing stresses.

We recall from the shear diagram of Sample Prob. 5.7 that V

max

4.50 kips. The actual width of the beam was given as b 5 3.5 in., and the

value obtained for its depth was h 5 14.55 in. Using Eq. (6.10) for the

maximum shearing stress in a narrow rectangular beam, we write

max

314.50 kips

213.5 in.2114.55 in.2

5 0.1325 ksi

Since t

max

, t

all

, the design obtained in Sample Prob. 5.7 is acceptable.

EXAMPLE 6.03

Knowing that the allowable shearing stress for the steel beam of Sample

Prob. 5.8 is t

all

5 90 MPa, check that the W360 3 32.9 shape obtained

in that sample problem is acceptable from the point of view of the shear-

ing stresses.

We recall from the shear diagram of Sample Prob. 5.8 that the maxi-

mum absolute value of the shear in the beam is |V|

max

5 58 kN. As we saw

in Sec. 6.4, it may be assumed in practice that the entire shear load is car-

ried by the web and that the maximum value of the shearing stress in the

beam can be obtained from Eq. (6.11). From Appendix C we find that for

a W360 3 32.9 shape the depth of the beam and the thickness of its web

are, respectively, d 5 349 mm and t

5 5.8 mm. We thus have

web

5 d t

349 mm

5.8 mm

5 2024 mm

Substituting the values of 0V 0

max

and A

into Eq. (6.11), we obtain

max

web

58 kN

2024 mm

5 28.7 MPa

Since t

max

, t

all

, the design obtained in Sample Prob. 5.8 is acceptable.

6.4 Shearing Stresses t

in Common

Types of Beams

bee80288_ch06_380-435.indd Page 389 10/28/10 7:59:19 PM user-f499bee80288_ch06_380-435.indd Page 389 10/28/10 7:59:19 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

390

Shearing Stresses in Beams

and Thin-Walled Members

*6.5 FURTHER DISCUSSION OF THE DISTRIBUTION OF

STRESSES IN A NARROW RECTANGULAR BEAM

h  2c

Fig. 6.17 Cantilever beam.

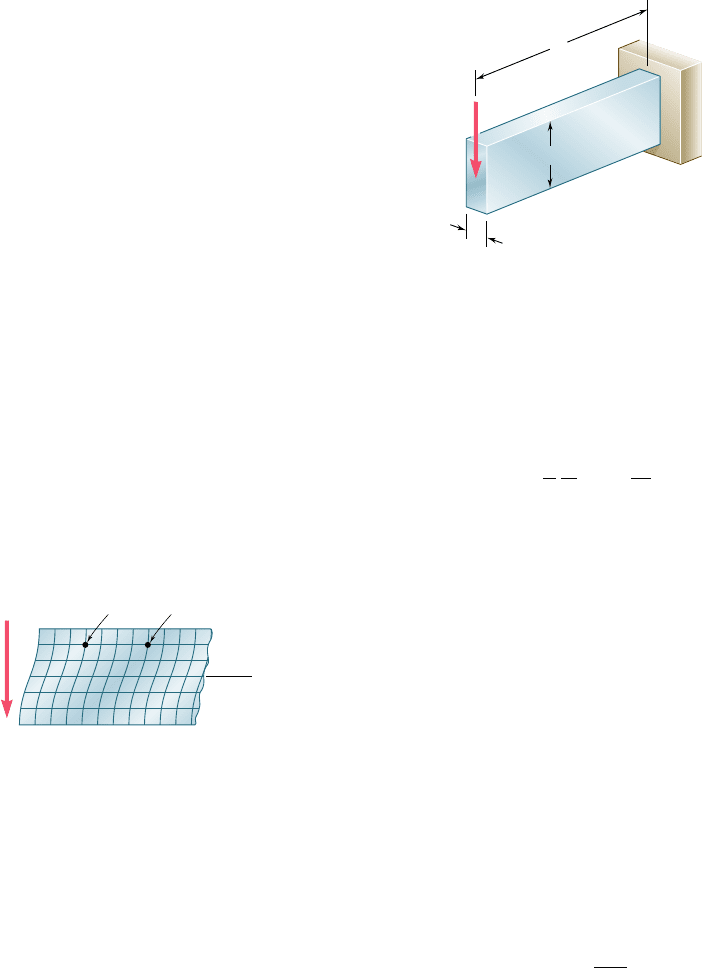
Consider a narrow cantilever beam of rectangular cross section of

width b and depth h subjected to a load P at its free end (Fig. 6.17).

Since the shear V in the beam is constant and equal in magnitude

to the load P, Eq. (6.9) yields

1 2

(6.12)

We note from Eq. (6.12) that the shearing stresses depend only upon

the distance y from the neutral surface. They are independent,

therefore, of the distance from the point of application of the load;

it follows that all elements located at the same distance from the

neutral surface undergo the same shear deformation (Fig. 6.18).

While plane sections do not remain plane, the distance between two

corresponding points D and D9 located in different sections remains

the same. This indicates that the normal strains P

, and thus the

normal stresses s

, are unaffected by the shearing stresses, and that

the assumption made in Sec. 5.1 is justified for the loading condition

of Fig. 6.17.

We conclude that our analysis of the stresses in a cantilever

beam of rectangular cross section, subjected to a concentrated load

P at its free end, is valid. The correct values of the shearing stresses

in the beam are given by Eq. (6.12), and the normal stresses at a

distance x from the free end are obtained by making M 5 2Px in

Eq. (5.2) of Sec. 5.1. We have

(6.13)

The validity of the above statement, however, depends upon

the end conditions. If Eq. (6.12) is to apply everywhere, then the

load P must be distributed parabolically over the free-end section.

Moreover, the fixed-end support must be of such a nature that it will

allow the type of shear deformation indicated in Fig. 6.18. The

D'D

Fig. 6.18 Deformation of

segment of cantilever beam.

bee80288_ch06_380-435.indd Page 390 10/28/10 7:59:20 PM user-f499bee80288_ch06_380-435.indd Page 390 10/28/10 7:59:20 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

391

resulting model (Fig. 6.19) is highly unlikely to be encountered in

practice. However, it follows from Saint-Venant’s principle that, for

other modes of application of the load and for other types of fixed-

end supports, Eqs. (6.12) and (6.13) still provide us with the correct

distribution of stresses, except close to either end of the beam.

When a beam of rectangular cross section is subjected to sev-

eral concentrated loads (Fig. 6.20), the principle of superposition can

be used to determine the normal and shearing stresses in sections

located between the points of application of the loads. However,

since the loads P

, P

, etc., are applied on the surface of the beam

and cannot be assumed to be distributed parabolically throughout

the cross section, the results obtained cease to be valid in the imme-

diate vicinity of the points of application of the loads.

When the beam is subjected to a distributed load (Fig. 6.21),

the shear varies with the distance from the end of the beam, and so

does the shearing stress at a given elevation y. The resulting shear

deformations are such that the distance between two corresponding

points of different cross sections, such as D

and D9

, or D

and D9

will depend upon their elevation. This indicates that the assumption

that plane sections remain plane, under which Eqs. (6.12) and (6.13)

were derived, must be rejected for the loading condition of Fig. 6.21.

The error involved, however, is small for the values of the span-depth

ratio encountered in practice.

We should also note that, in portions of the beam located under

a concentrated or distributed load, normal stresses s

will be exerted

on the horizontal faces of a cubic element of material, in addition to

the stresses t

shown in Fig. 6.2.

Fig. 6.20 Cantilever beam.



Fig. 6.19 Deformation of cantilever

beam with concentrated load.

Fig. 6.21 Deformation of cantilever beam

with distributed load.

6.5 Further Discussion of the Distribution of

Stresses in a Narrow Rectangular Beam

bee80288_ch06_380-435.indd Page 391 10/28/10 7:59:25 PM user-f499bee80288_ch06_380-435.indd Page 391 10/28/10 7:59:25 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

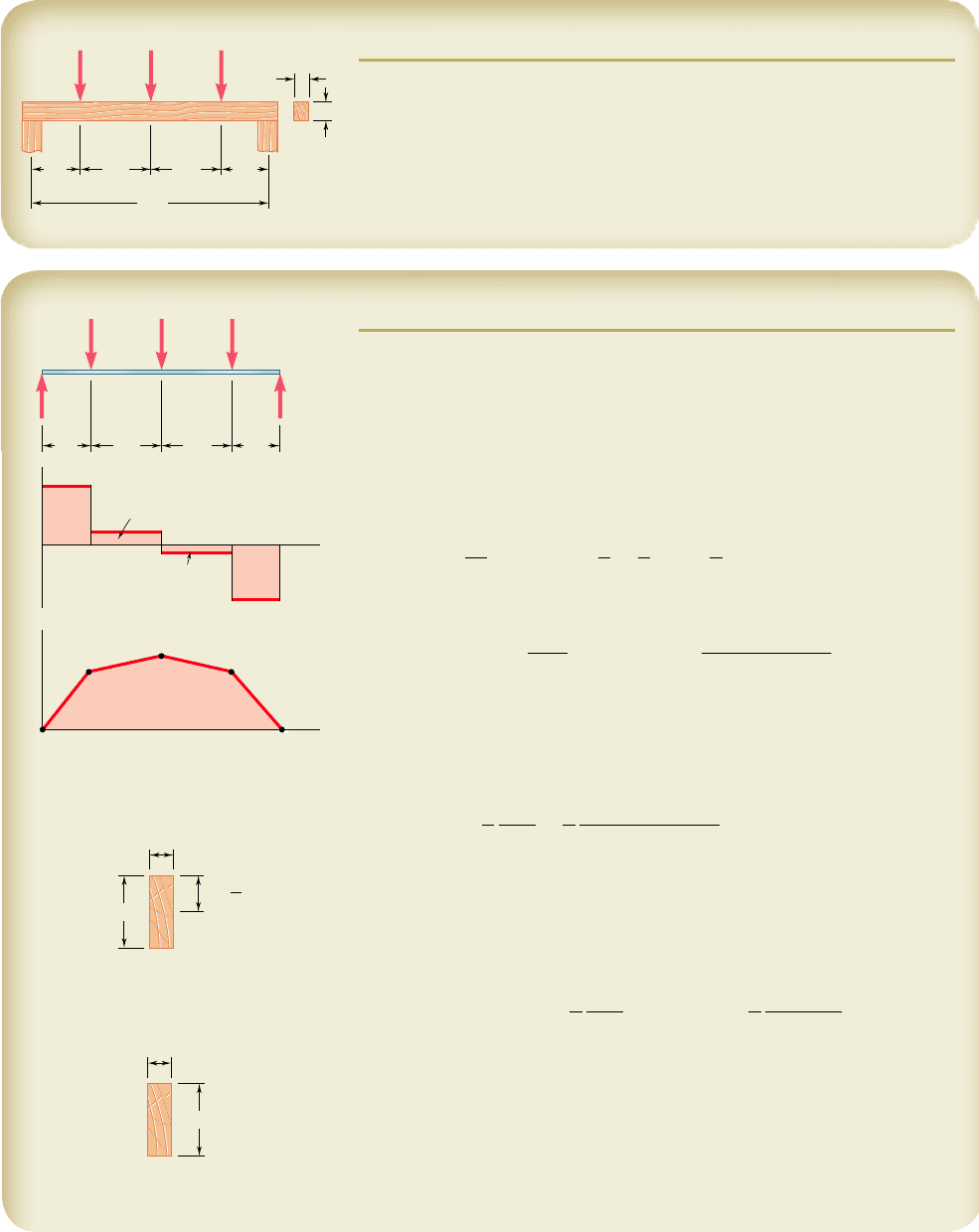
SAMPLE PROBLEM 6.1

Beam AB is made of three planks glued together and is subjected, in its

plane of symmetry, to the loading shown. Knowing that the width of each

glued joint is 20 mm, determine the average shearing stress in each joint

at section n-n of the beam. The location of the centroid of the section is

given in the sketch and the centroidal moment of inertia is known to be

I 5 8.63 3 10

SOLUTION

Vertical Shear at Section n-n. Since the beam and loading are both

symmetric with respect to the center of the beam, we have A 5

B 5 1.5 kN c.

Considering the portion of the beam to the left of section n-n as a free body,

we write

1xg F

5 0: 1.5 kN 2 V 5 0V 5 1.5 kN

Shearing Stress in Joint a. We pass the section a-a through the glued

joint and separate the cross-sectional area into two parts. We choose to

determine Q by computing the first moment with respect to the neutral axis

of the area above section a-a.

Q 5 A

5 310.100 m210.020 m2410.0417 m25 83.4 3 10

Recalling that the width of the glued joint is t 5 0.020 m, we use Eq. (6.7)

to determine the average shearing stress in the joint.

ave

11500 N2183.4 3 10

18.63 3 10

210.020 m2

ave

5 725 kPab

Shearing Stress in Joint b. We now pass section b-b and compute Q

by using the area below the section.

Q 5 A

5 310.060 m210.020 m2410.0583 m25 70.0 3 10

ave

11500 N2170.0 3 10

18.63 3 10

210.020 m2

ave

5 608 kPab

0.4 m 0.4 m

0.2 m

1.5 kN1.5 kN

1.5 kN

 1.5 kN

B  1.5 kN

A  1.5 kN

1.5 kN

0.100 m

0.020 m

Neutral axis

 0.0417 m

Neutral axis

0.020 m

0.060 m

 0.0583 m

100 mm

68.3 mm

Joint a

Joint b

60 mm

20 mm

80 mm

392

bee80288_ch06_380-435.indd Page 392 10/28/10 7:59:31 PM user-f499bee80288_ch06_380-435.indd Page 392 10/28/10 7:59:31 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

393

SAMPLE PROBLEM 6.2

A timber beam AB of span 10 ft and nominal width 4 in. (actual width 5

3.5 in.) is to support the three concentrated loads shown. Knowing that for

the grade of timber used s

all

5 1800 psi and t

all

5 120 psi, determine the

minimum required depth d of the beam.

2.5 kips 1 kip 2.5 kips

2 ft 2 ft

3.5 in.

3 ft

10 ft

3 ft

SOLUTION

Maximum Shear and Bending Moment. After drawing the shear and

bending-moment diagrams, we note that

max

5 7.5

ip ?

t 5 90

ip ? in.

max

5 3 kips

Design Based on Allowable Normal Stress. We first express the

elastic section modulus S in terms of the depth d. We have

I 5

S 5

13.52d

5 0.5833d

For M

max

5 90

ip ? in. and s

all

5 1800 psi, we write

S 5

max

all

 0.5833d

90 3 10

lb ? in.

1800 psi

5 85

7

5 9

26 in

We have satisfied the requirement that s

# 1800 psi.

Check Shearing Stress. For V

max

5 3 kips and d 5 9.26 in., we find

max

3000 lb

13.5 in.219.26 in.2

t

5 138.8 psi

Since t

all

5 120 psi, the depth d 5 9.26 in. is not acceptable and we must

redesign the beam on the basis of the requirement that t

# 120 psi.

Design Based on Allowable Shearing Stress. Since we now know

that the allowable shearing stress controls the design, we write

5 t

all

max

120 psi 5

3000 lb

13.5 in.2d

5 10

71 in

b

The normal stress is, of course, less than s

all

5 1800 psi, and the depth of

10.71 in. is fully acceptable.

Comment. Since timber is normally available in depth increments of

2 in., a 4 3 12-in. nominal size timber should be used. The actual cross

section would then be 3.5 3 11.25 in.

BCDE

2.5 kips 1 kip 2.5 kips

3 kips

6 kip

7.5 kip

3 kips

3 kips

0.5 kip

0.5 kip

2 ft

2 ft3 ft

(1.5)

(1.5)

(6)

(6)

3 ft

b  3.5 in.

c 

3.5 in.

11.25 in.

4 in.  12 in.

Nominal size

bee80288_ch06_380-435.indd Page 393 11/13/10 12:25:30 AM user-f499bee80288_ch06_380-435.indd Page 393 11/13/10 12:25:30 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch06/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch06

Apago PDF Enhancer

PROBLEMS

394394

6.1 Three boards, each of 1.5 3 3.5-in. rectangular cross section, are

nailed together to form a beam that is subjected to a vertical shear

of 250 lb. Knowing that the spacing between each pair of nails is

2.5 in., determine the shearing force in each nail.

1.5 in.

2.5 in.

1.5 in.

3.5 in.

Fig. P6.1

2 in.

6 in.

2 in.

4 in.

Fig. P6.2

6.3 Three boards are nailed together to form a beam shown, which is

subjected to a vertical shear. Knowing that the spacing between the

nails is s 5 75 mm and that the allowable shearing force in each nail

is 400 N, determine the allowable shear when w 5 120 mm.

6.4 Solve Prob. 6.3, assuming that the width of the top and bottom

boards is changed to w 5 100 mm.

60 mm

200 mm

60 mm

Fig. P6.3

6.2 Three boards, each 2 in. thick, are nailed together to form a beam

that is subjected to a vertical shear. Knowing that the allowable

shearing force in each nail is 150 lb, determine the allowable shear

if the spacing s between the nails is 3 in.

bee80288_ch06_380-435.indd Page 394 10/28/10 7:59:50 PM user-f499bee80288_ch06_380-435.indd Page 394 10/28/10 7:59:50 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

395

Problems

6.5 The American Standard rolled-steel beam shown has been rein-

forced by attaching to it two 16 3 200-mm plates, using 18-mm-

diameter bolts spaced longitudinally every 120 mm. Knowing that

the average allowable shearing stress in the bolts is 90 MPa, deter-

mine the largest permissible vertical shearing force.

16  200 mm

S310  52

Fig. P6.5

S10  25.4

C8  13.7

Fig. P6.7

6.8 The composite beam shown is fabricated by connecting two W6 3

20 rolled-steel members, using bolts of

-in. diameter spaced lon-

gitudinally every 6 in. Knowing that the average allowable shearing

stress in the bolts is 10.5 ksi, determine the largest allowable verti-

cal shear in the beam.

Fig. P6.8

6.6 Solve Prob. 6.5, assuming that the reinforcing plates are only 12 mm

thick.

6.7 A column is fabricated by connecting the rolled-steel members

shown by bolts of

-in. diameter spaced longitudinally every 5 in.

Determine the average shearing stress in the bolts caused by a

shearing force of 30 kips parallel to the y axis.

bee80288_ch06_380-435.indd Page 395 10/28/10 8:00:04 PM user-f499bee80288_ch06_380-435.indd Page 395 10/28/10 8:00:04 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

396

Shearing Stresses in Beams

and Thin-Walled Members

6.9 through 6.12 For the beam and loading shown, consider sec-

tion n-n and determine (a) the largest shearing stress in that section,

(b) the shearing stress at point a.

1 ft

2 ft 2 ft 2 ft 2 ft

0.375 in.

1 in.

0.6 in.

10 in.

15 kips 20 kips 15 kips

Fig. P6.9

1.5 m

100 mm

200 mm

40 mm

12 mm

150 mm

0.3 m

10 kN

Fig. P6.10

180

0.6 m

0.9 m

Dimensions in mm

0.9 m

160 kN

100

Fig. P6.11

8 in.

16 in. 12 in. 16 in.

4 in.

10 kips 10 kips

in.

Fig. P6.12

bee80288_ch06_380-435.indd Page 396 10/28/10 8:00:13 PM user-f499bee80288_ch06_380-435.indd Page 396 10/28/10 8:00:13 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles