Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

367

Problems

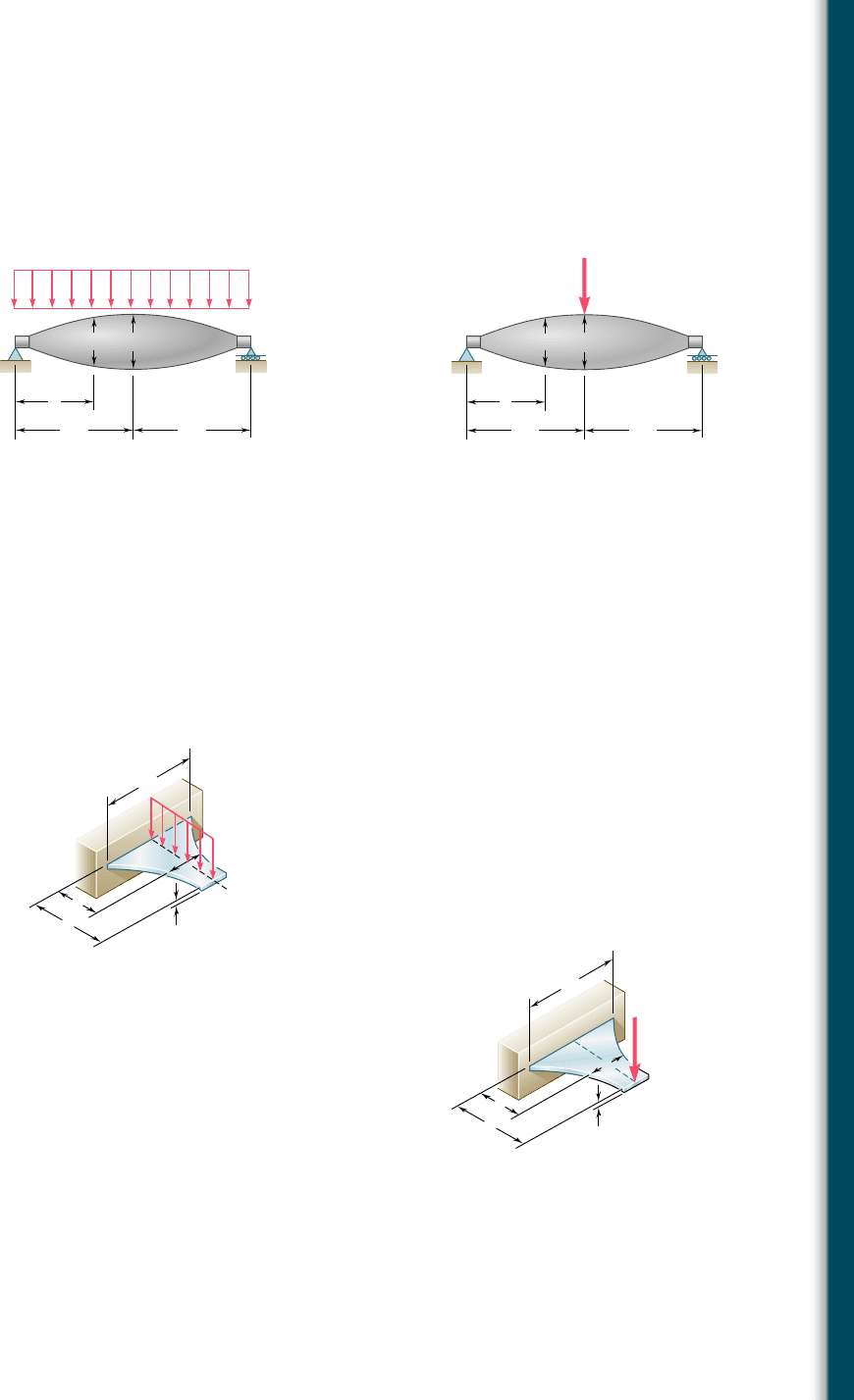
5.136 and 5.137 A machine element of cast aluminum and in the

shape of a solid of revolution of variable diameter d is being designed

to support the load shown. Knowing that the machine element is

to be of constant strength, express d in terms of x, L, and d

L/2 L/2

Fig. P5.136

L/2 L/2

Fig. P5.137

5.138 A cantilever beam AB consisting of a steel plate of uniform depth h

and variable width b is to support the distributed load w along its

centerline AB. (a) Knowing that the beam is to be of constant

strength, express b in terms of x, L, and b

. (b) Determine the maxi-

mum allowable value of w if L 5 15 in., b

5 8 in., h 5 0.75 in.,

and s

all

5 24 ksi.

Fig. P5.138

Fig. P5.139

5.139 A cantilever beam AB consisting of a steel plate of uniform depth

h and variable width b is to support the concentrated load P at

point A. (a) Knowing that the beam is to be of constant strength,

express b in terms of x, L, and b

. (b) Determine the smallest

allowable value of h if L 5 300 mm, b

5 375 mm, P 5 14.4 kN,

and s

all

5 160 MPa.

5.140 Assuming that the length and width of the cover plates used with

the beam of Sample Prob. 5.12 are, respectively, l 5 4 m and b 5

285 mm, and recalling that the thickness of each plate is 16 mm,

determine the maximum normal stress on a transverse section

(a) through the center of the beam, (b) just to the left of D.

bee80288_ch05_314-379.indd Page 367 10/27/10 9:58:50 PM user-f499bee80288_ch05_314-379.indd Page 367 10/27/10 9:58:50 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

368

Analysis and Design of Beams for Bending

5.141 Knowing that s

all

5 150 MPa, determine the largest concentrated

load P that can be applied at end E of the beam shown.

W410 ⫻ 85

18 ⫻ 220 mm

2.25 m 1.25 m

2.2 m

4.8 m

Fig. P5.141

5.142 Two cover plates, each

in. thick, are welded to a W30 3 99 beam

as shown. Knowing that l 5 9 ft and b 5 12 in., determine the

maximum normal stress on a transverse section (a) through the

center of the beam, (b) just to the left of D.

W30 × 99

16 ft

30 kips/ft

in.

Fig. P5.142 and P5.143

7.5 mm

W460 × 74

8 m

40 kN/m

Fig. P5.144 and P5.145

5.143 Two cover plates, each

in. thick, are welded to a W30 3 99 beam

as shown. Knowing that s

all

5 22 ksi for both the beam and the

plates, determine the required value of (a) the length of the plates,

(b) the width of the plates.

5.144 Two cover plates, each 7.5 mm thick, are welded to a W460 3 74

beam as shown. Knowing that l 5 5 m and b 5 200 mm, determine

the maximum normal stress on a transverse section (a) through the

center of the beam, (b) just to the left of D.

5.145 Two cover plates, each 7.5 mm thick, are welded to a W460 3 74

beam as shown. Knowing that s

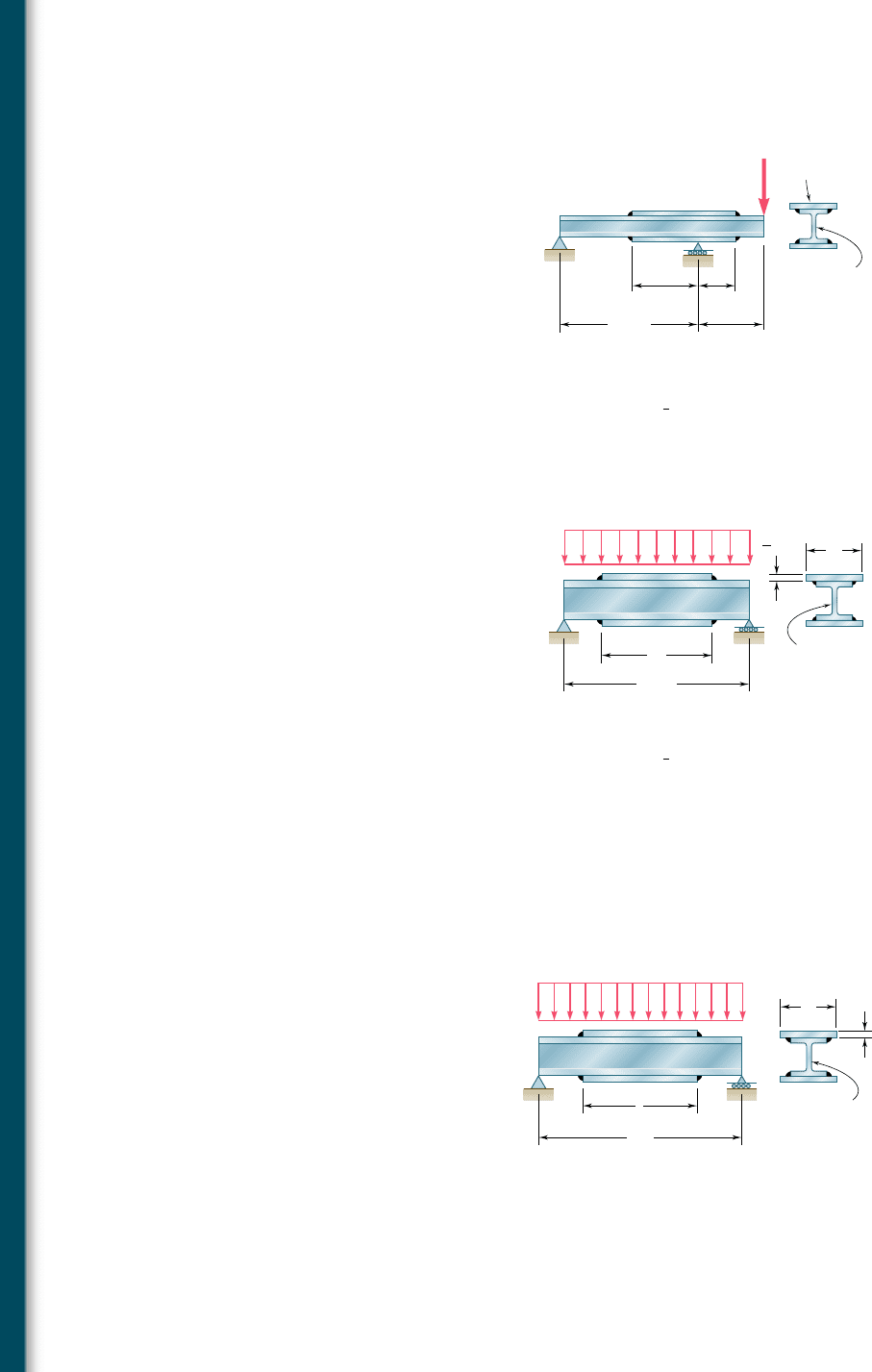
all

5 150 MPa for both the beam

and the plates, determine the required value of (a) the length of

the plates, (b) the width of the plates.

bee80288_ch05_314-379.indd Page 368 10/27/10 9:58:59 PM user-f499bee80288_ch05_314-379.indd Page 368 10/27/10 9:58:59 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

369

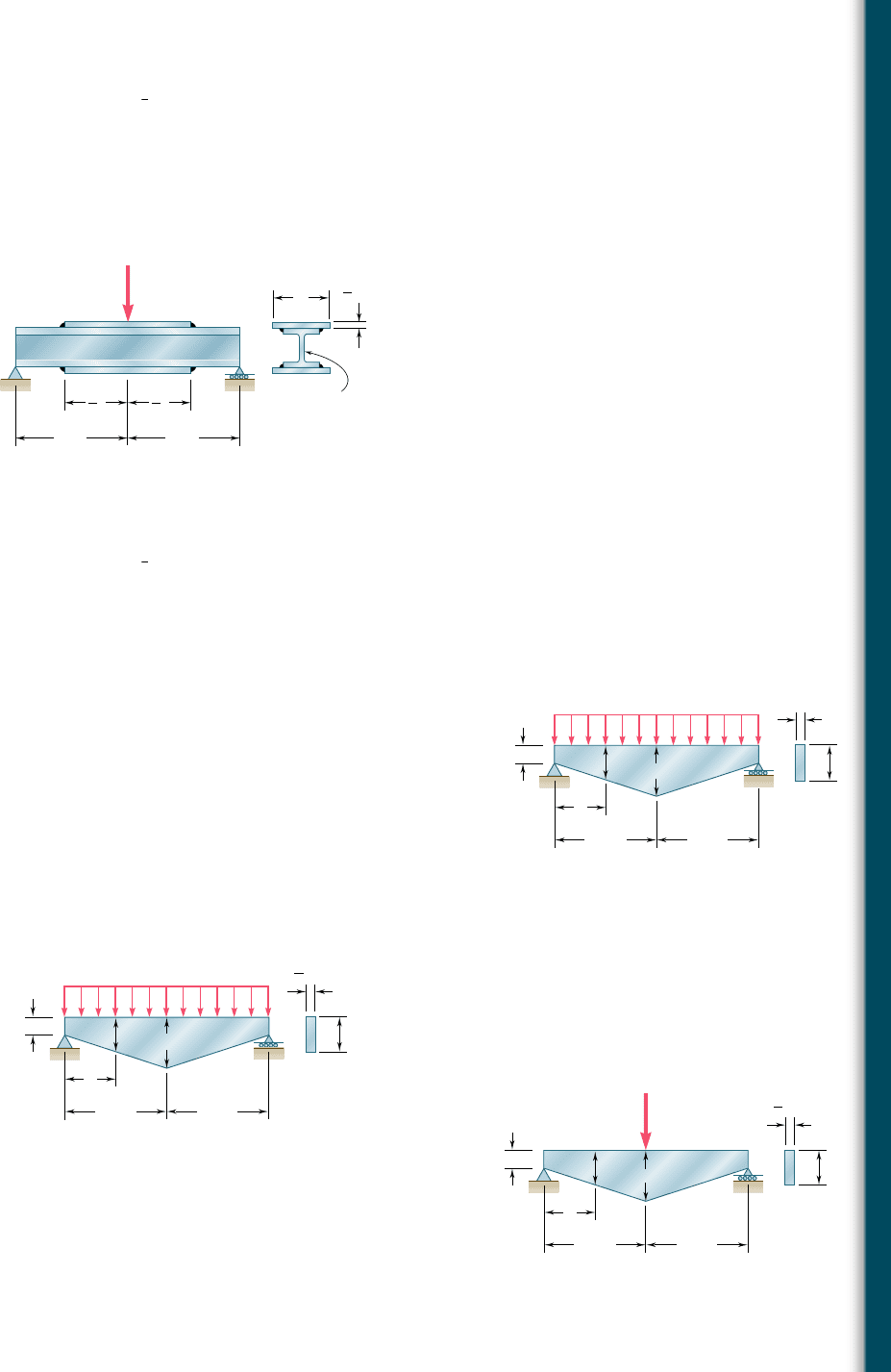
Problems

5.147 Two cover plates, each

in. thick, are welded to a W27 3 84 beam

as shown. Knowing that s

all

5 24 ksi for both the beam and the

plates, determine the required value of (a) the length of the plates,

(b) the width of the plates.

5.148 For the tapered beam shown, determine (a) the transverse section

in which the maximum normal stress occurs, (b) the largest distrib-

uted load w that can be applied, knowing that s

all

5 140 MPa.

5.149 For the tapered beam shown, knowing that w 5 160 kN/m, deter-

mine (a) the transverse section in which the maximum normal

stress occurs, (b) the corresponding value of the normal stress.

5.150 For the tapered beam shown, determine (a) the transverse section

in which the maximum normal stress occurs, (b) the largest distrib-

uted load w that can be applied, knowing that s

all

5 24 ksi.

in.

EDC

W27 × 84

9 ft

160 kips

9 ft

Fig. P5.146 and P5.147

5.146 Two cover plates, each

in. thick, are welded to a W27 3 84 beam

as shown. Knowing that l 5 10 ft and b 5 10.5 in., determine the

maximum normal stress on a transverse section (a) through the

center of the beam, (b) just to the left of D.

0.6 m

120 mm

0.6 m

300 mm

20 mm

Fig. P5.148 and P5.149

30 in.

4 in.

30 in.

in.

8 in.

Fig. P5.150

5.151 For the tapered beam shown, determine (a) the transverse section

in which the maximum normal stress occurs, (b) the largest con-

centrated load P that can be applied, knowing that s

all

5 24 ksi.

30 in.

4 in.

ABC

30 in.

8 in.

in.

Fig. P5.151

bee80288_ch05_314-379.indd Page 369 10/27/10 9:59:06 PM user-f499bee80288_ch05_314-379.indd Page 369 10/27/10 9:59:06 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

370

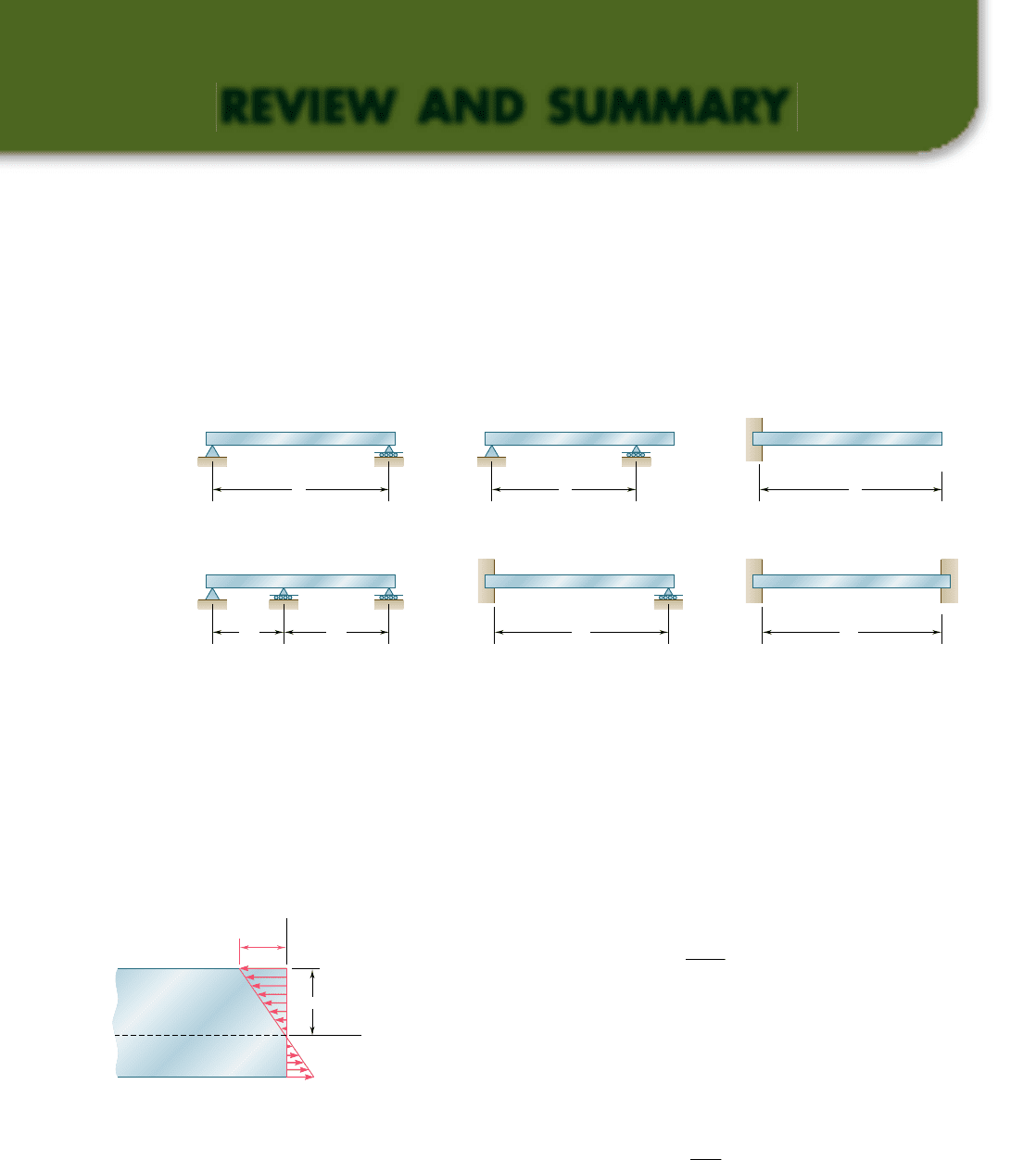
This chapter was devoted to the analysis and design of beams under

transverse loadings. Such loadings can consist of concentrated loads

or distributed loads and the beams themselves are classified accord-

ing to the way they are supported (Fig. 5.22). Only statically deter-

minate beams were considered in this chapter, where all support

reactions can be determined by statics. The analysis of statically inde-

terminate beams is postponed until Chap. 9.

Considerations for the design of

prismatic beams

Considerations for the design of

prismatic beams

(a) Simply supported beam

Statically

Determinate

Beams

Statically

Indeterminate

Beams

(d) Continuous beam

(b) Overhanging beam

Beam fixed at one end

and simply supported

at the other end

(e)

( f ) Fixed beam

Fig. 5.22

␴

Neutral surface

Fig. 5.23

While transverse loadings cause both bending and shear in a beam,

the normal stresses caused by bending are the dominant criterion in

the design of a beam for strength [Sec. 5.1]. Therefore, this chapter

dealt only with the determination of the normal stresses in a beam,

the effect of shearing stresses being examined in the next one.

We recalled from Sec. 4.4 the flexure formula for the determi-

nation of the maximum value s

of the normal stress in a given

section of the beam,

(5.1)

where I is the moment of inertia of the cross section with respect to a

centroidal axis perpendicular to the plane of the bending couple M and

c is the maximum distance from the neutral surface (Fig. 5.23). We

also recalled from Sec. 4.4 that, introducing the elastic section modulus

S 5 Iyc of the beam, the maximum value s

of the normal stress in

the section can be expressed as

(5.3)

It follows from Eq. (5.1) that the maximum normal stress occurs in

the section where |M| is largest, at the point farthest from the neutral

Normal stresses due to bending

Shear and bending-moment

diagrams

REVIEW AND SUMMARY

bee80288_ch05_314-379.indd Page 370 10/27/10 9:59:16 PM user-f499bee80288_ch05_314-379.indd Page 370 10/27/10 9:59:16 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

371

axis. The determination of the maximum value of |M| and of the critical

section of the beam in which it occurs is greatly simplified if we draw

a shear diagram and a bending-moment diagram. These diagrams rep-

resent, respectively, the variation of the shear and of the bending

moment along the beam and were obtained by determining the values

of V and M at selected points of the beam [Sec. 5.2]. These values

were found by passing a section through the point where they were

to be determined and drawing the free-body diagram of either of the

portions of beam obtained in this fashion. To avoid any confusion

regarding the sense of the shearing force V and of the bending couple

M (which act in opposite sense on the two portions of the beam), we

followed the sign convention adopted earlier in the text as illustrated

in Fig. 5.24 [Examples 5.01 and 5.02, Sample Probs. 5.1 and 5.2].

The construction of the shear and bending-moment diagrams is

facilitated if the following relations are taken into account [Sec. 5.3].

Denoting by w the distributed load per unit length (assumed positive

if directed downward), we wrote

52w

5 V

(5.5, 5.7)

or, in integrated form,

2 V

area under load curve between C and D

(5.69)

2 M

5 area under shear curve between C and D (5.89)

Equation (5.69) makes it possible to draw the shear diagram of a beam

from the curve representing the distributed load on that beam and the

value of V at one end of the beam. Similarly, Eq. (5.89) makes it pos-

sible to draw the bending-moment diagram from the shear diagram

and the value of M at one end of the beam. However, concentrated

loads introduce discontinuities in the shear diagram and concentrated

couples in the bending-moment diagram, none of which is accounted

for in these equations [Sample Probs. 5.3 and 5.6]. Finally, we noted

from Eq. (5.7) that the points of the beam where the bending moment

is maximum or minimum are also the points where the shear is zero

[Sample Prob. 5.4].

A proper procedure for the design of a prismatic beam was

described in Sec. 5.4 and is summarized here:

Having determined s

all

for the material used and assuming that

the design of the beam is controlled by the maximum normal stress

in the beam, compute the minimum allowable value of the section

modulus:

min

max

(5.9)

For a timber beam of rectangular cross section, S 5

where b is the width of the beam and h its depth. The dimensions

of the section, therefore, must be selected so that

$ S

min

For a rolled-steel beam, consult the appropriate table in Appen-

dix C. Of the available beam sections, consider only those with a

Relations among load, shear,

and bending moment

Relations among load, shear,

and bending moment

Design of prismatic beamsDesign of prismatic beams

Review and Summary

(a) Internal forces

(

ositive shear and

ositive bendin

moment)

Fig. 5.24

bee80288_ch05_314-379.indd Page 371 11/16/10 7:00:20 PM user-f499bee80288_ch05_314-379.indd Page 371 11/16/10 7:00:20 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

372

Analysis and Design of Beams for Bending

section modulus S $ S

min

and select from this group the section with

the smallest weight per unit length. This is the most economical of

the sections for which S $ S

min

In Sec. 5.5, we discussed an alternative method for the determina-

tion of the maximum values of the shear and bending moment based

on the use of the singularity functions

x 2 a

. By definition, and

for n $ 0, we had

Hx 2 aI

1x 2 a2

when x $ a

0 when x , a

(5.14)

We noted that whenever the quantity between brackets is positive or

zero, the brackets should be replaced by ordinary parentheses, and

whenever that quantity is negative, the bracket itself is equal to zero.

We also noted that singularity functions can be integrated and dif-

ferentiated as ordinary binomials. Finally, we observed that the sin-

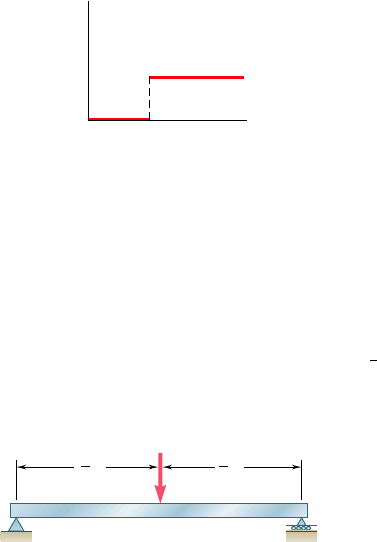
gularity function corresponding to n 5 0 is discontinuous at x 5 a

(Fig. 5.25). This function is called the step function. We wrote

Hx 2 aI

1 when x $ a

0 when x , a

(5.15)

Singularity functionsSingularity functions

Step functionStep function

(a) n ⫽ 0

⬍ x ⫺ a ⬎

Fig. 5.25

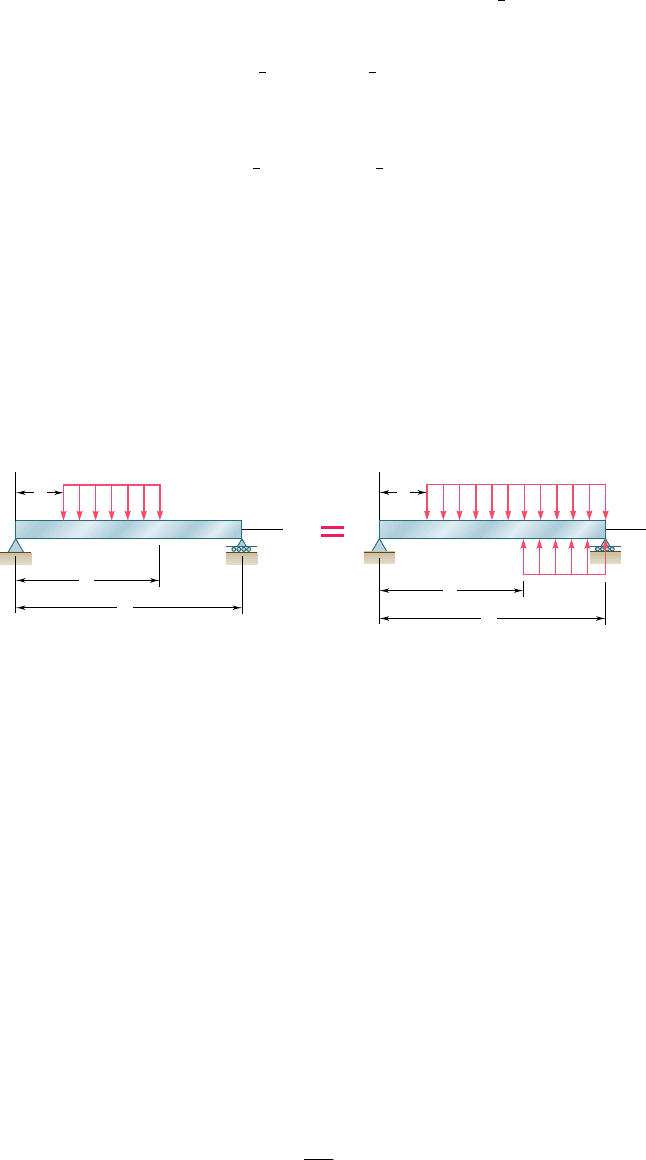
The use of singularity functions makes it possible to represent the

shear or the bending moment in a beam by a single expression, valid

at any point of the beam. For example, the contribution to the shear

of the concentrated load P applied at the midpoint C of a simply

supported beam (Fig. 5.26) can be represented by 2P

x 2

, since

Using singularity functions to

express shear and bending moment

Using singularity functions to

express shear and bending moment

Fig. 5.26

bee80288_ch05_314-379.indd Page 372 11/12/10 7:24:36 PM user-f499bee80288_ch05_314-379.indd Page 372 11/12/10 7:24:36 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch05/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch05

Apago PDF Enhancer

373

this expression is equal to zero to the left of C, and to 2P to the

right of C. Adding the contribution of the reaction R

P at A, we

express the shear at any point of the beam as

P 2 P

x 2

The bending moment is obtained by integrating this expression:

M1x25

Px 2 P

x 2

The singularity functions representing, respectively, the load, shear,

and bending moment corresponding to various basic loadings were

given in Fig. 5.18 on page 353. We noted that a distributed loading

that does not extend to the right end of the beam, or which is dis-

continuous, should be replaced by an equivalent combination of

open-ended loadings. For instance, a uniformly distributed load

extending from x 5 a to x 5 b (Fig. 5.27) should be expressed as

w1x25 w

x 2 a

2 w

x 2 b

Equivalent open-ended loadingsEquivalent open-ended loadings

Fig. 5.27

⫺ w

Review and Summary

The contribution of this load to the shear and to the bending moment

can be obtained through two successive integrations. Care should be

taken, however, to also include in the expression for V(x) the contribu-

tion of concentrated loads and reactions, and to include in the expres-

sion for M(x) the contribution of concentrated couples [Examples 5.05

and 5.06, Sample Probs. 5.9 and 5.10]. We also observed that singular-

ity functions are particularly well suited to the use of computers.

We were concerned so far only with prismatic beams, i.e., beams of

uniform cross section. Considering in Sec. 5.6 the design of nonpris-

matic beams, i.e., beams of variable cross section, we saw that by

selecting the shape and size of the cross section so that its elastic

section modulus S 5 Iyc varied along the beam in the same way as

the bending moment M, we were able to design beams for which

at each section was equal to s

all

. Such beams, called beams of

constant strength, clearly provide a more effective use of the material

than prismatic beams. Their section modulus at any section along

the beam was defined by the relation

S 5

(5.18)

Nonprismatic beamsNonprismatic beams

Beams of constant strengthBeams of constant strength

bee80288_ch05_314-379.indd Page 373 11/12/10 7:24:41 PM user-f499bee80288_ch05_314-379.indd Page 373 11/12/10 7:24:41 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch05/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch05

Apago PDF Enhancer

374

REVIEW PROBLEMS

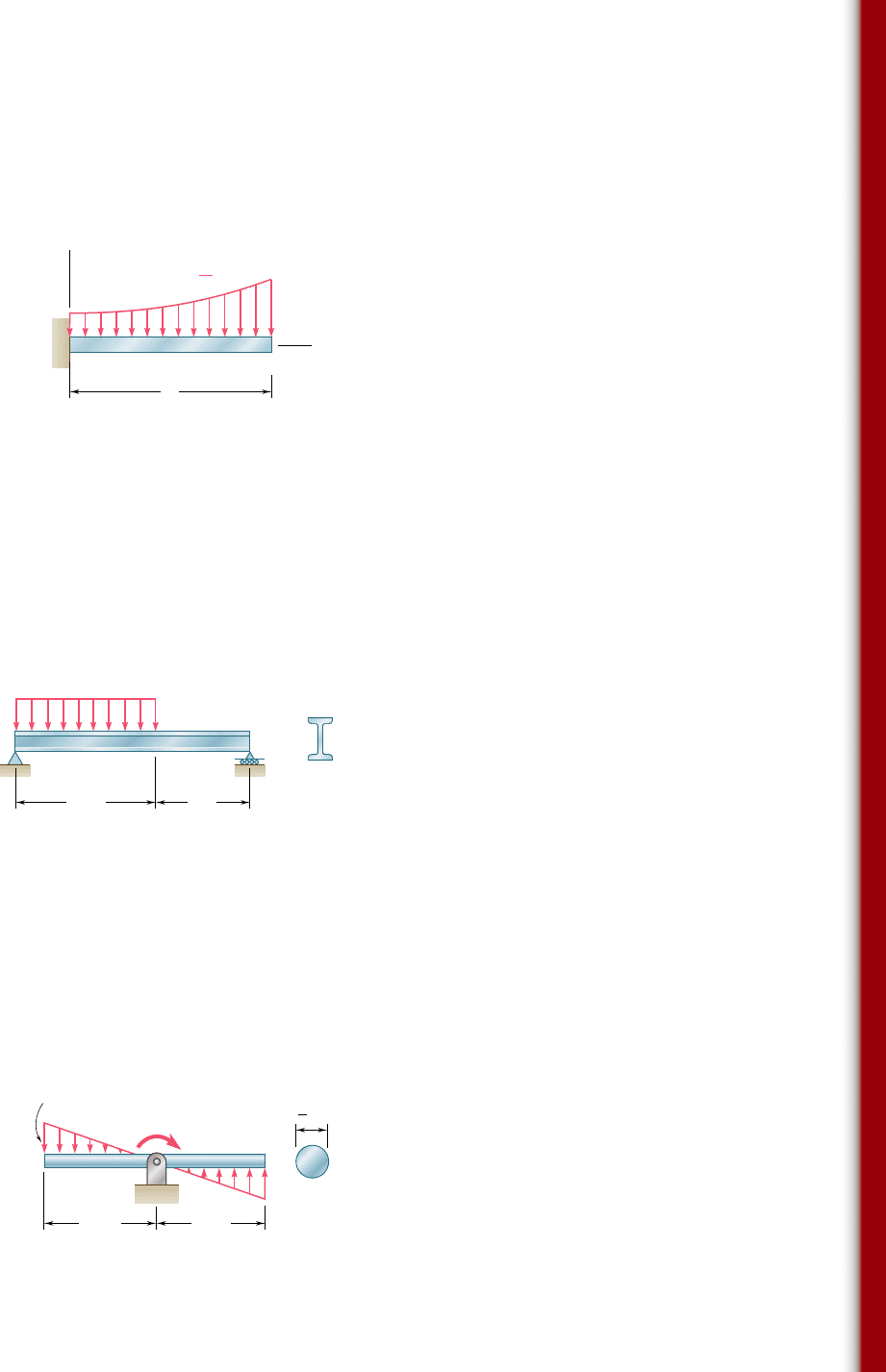
5.152 Draw the shear and bending-moment diagrams for the beam and

loading shown, and determine the maximum absolute value (a) of

the shear, (b) of the bending moment.

400 lb 1600 lb 400 lb

12 in. 12 in. 12 in. 12 in.

8 in.

DEF

Fig. P5.152

5.154 Determine (a) the distance a for which the maximum absolute

value of the bending moment in the beam is as small as possible,

(b) the corresponding maximum normal stress due to bending.

(See hint of Prob. 5.27.)

7 @ 200 mm ⫽ 1400 mm

Hinge

30 mm

20 mm

CBDEFG

300 N 300 N 300 N40 N

Fig. P5.153

5 ft8 ft

W14 ⫻ 22

10 kips5 kips

Fig. P5.154

5.153 Draw the shear and bending-moment diagrams for the beam and

loading shown and determine the maximum normal stress due to

bending.

bee80288_ch05_314-379.indd Page 374 10/27/10 9:59:38 PM user-f499bee80288_ch05_314-379.indd Page 374 10/27/10 9:59:38 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

375

Review Problems

5.155 Determine (a) the equations of the shear and bending-moment

curves for the beam and loading shown, (b) the maximum absolute

value of the bending moment in the beam.

w ⫽ w

l ⫹

(

Fig. P5.155

5.156 Draw the shear and bending-moment diagrams for the beam and

loading shown and determine the maximum normal stress due to

bending.

16 kN/m

1 m1.5 m

S150 ⫻ 18.6

Fig. P5.156

5.157 Knowing that beam AB is in equilibrium under the loading shown,

draw the shear and bending-moment diagrams and determine the

maximum normal stress due to bending.

Fig. P5.157

1.2 ft 1.2 ft

⫽ 50 lb/ft

in.

bee80288_ch05_314-379.indd Page 375 10/27/10 10:00:31 PM user-f499bee80288_ch05_314-379.indd Page 375 10/27/10 10:00:31 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

376

Analysis and Design of Beams for Bending

5.159 Knowing that the allowable stress for the steel used is 160 MPa,

select the most economical wide-flange beam to support the loading

shown.

5.160 Determine the largest permissible value of P for the beam and

loading shown, knowing that the allowable normal stress is 18 ksi

in tension and 218 ksi in compression.

10 in.

60 in. 60 in.

1 in.

5 in.

1 in.

7 in.

DCB

Fig. P5.160

0.8 m 0.8 m

2.4 m

50 kN/m

Fig. P5.159

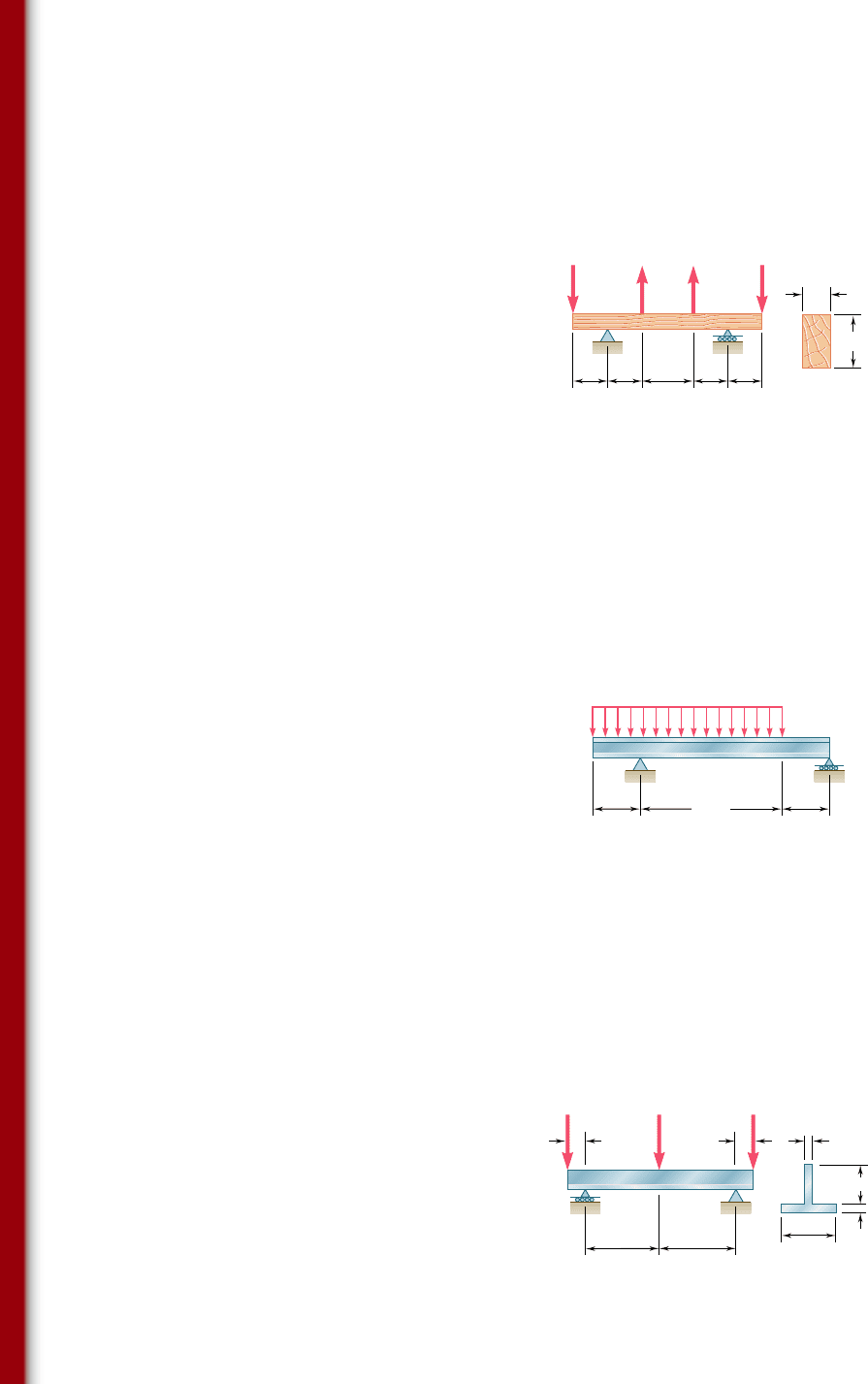
5.158 For the beam and loading shown, design the cross section of the

beam, knowing that the grade of timber used has an allowable

normal stress of 1750 psi.

4.8 kips

2 kips 2 kips

2 ft 2 ft 3 ft 2 ft 2 ft

9.5 in.

BC DE

Fig. P5.158

bee80288_ch05_314-379.indd Page 376 10/27/10 10:00:44 PM user-f499bee80288_ch05_314-379.indd Page 376 10/27/10 10:00:44 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles