Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

337

5.51 and 5.52 Determine (a) the equations of the shear and

bending-moment curves for the beam and loading shown, (b) the

maximum absolute value of the bending moment in the beam.

w  w

Fig. P5.51

w  w

sin



Fig. P5.52

5.53 Determine (a) the equations of the shear and bending-moment

curves for the beam and loading shown, (b) the maximum absolute

value of the bending moment in the beam.

w  w

cos



Fig. P5.53

6 ft 6 ft

2 ft

2 kips/ft

6 kips

W8  31

Fig. P5.54

1 m

4 m

160 mm

140 mm

3 kN/m

2 kN

Fig. P5.55

5.56 and 5.57 Draw the shear and bending-moment diagrams for

the beam and loading shown and determine the maximum normal

stress due to bending.

80 lb /ft

1600 lb

1.5 ft

9 ft

11.5 in.

1.5 in.

Fig. P5.56

250 kN 150 kN

2 m 2 m 2 m

W410  114

Fig. P5.57

5.54 and 5.55 Draw the shear and bending-moment diagrams for

the beam and loading shown and determine the maximum normal

stress due to bending.

Problems

bee80288_ch05_314-379.indd Page 337 10/27/10 9:53:33 PM user-f499bee80288_ch05_314-379.indd Page 337 10/27/10 9:53:33 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

338

Analysis and Design of Beams for Bending

5.58 and 5.59 Draw the shear and bending-moment diagrams for

the beam and loading shown and determine the maximum normal

stress due to bending.

80 kN/m

W250  80

1.2 m 1.2 m1.6 m

60 kN · m 12 kN · m

8 in.

20 in.

3 in.

800 lb/in.

2 in.

1 in.

Fig. P5.59Fig. P5.58

5.60 Beam AB, of length L and square cross section of side a, is sup-

ported by a pivot at C and loaded as shown. (a) Check that the

beam is in equilibrium. (b) Show that the maximum stress due to

bending occurs at C and is equal to w

y(1.5a)

Fig. P5.60

400 kN/m

W200  22.5

0.3 m 0.3 m0.4 m

Fig. P5.61

480 lb/ft

1 ft 1 ft

1.5 ft 1.5 ft

W8  31

8 ft

CDEF

Fig. P5.62

5.61 Knowing that beam AB is in equilibrium under the loading shown,

draw the shear and bending-moment diagrams and determine the

maximum normal stress due to bending.

*5.62 The beam AB supports a uniformly distributed load of 480 lb/ft

and two concentrated loads P and Q. The normal stress due to

bending on the bottom edge of the lower flange is 114.85 ksi at

D and 110.65 ksi at E. (a) Draw the shear and bending-moment

diagrams for the beam. (b) Determine the maximum normal stress

due to bending that occurs in the beam.

bee80288_ch05_314-379.indd Page 338 10/27/10 9:53:49 PM user-f499bee80288_ch05_314-379.indd Page 338 10/27/10 9:53:49 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

*5.63 Beam AB supports a uniformly distributed load of 2 kN/m and two

concentrated loads P and Q. It has been experimentally deter-

mined that the normal stress due to bending in the bottom edge

of the beam is 256.9 MPa at A and 229.9 MPa at C. Draw the

shear and bending-moment diagrams for the beam and determine

the magnitudes of the loads P and Q.

*5.64 The beam AB supports two concentrated loads P and Q. The

normal stress due to bending on the bottom edge of the beam

is 155 MPa at D and 137.5 MPa at F. (a) Draw the shear and

bending-moment diagrams for the beam. (b) Determine the maxi-

mum normal stress due to bending that occurs in the beam.

2 kN/m

0.1 m 0.1 m 0.125 m

36 mm

18 mm

Fig. P5.63

Fig. P5.64

0.4 m

24 mm

0.2 m

0.5 m 0.5 m

60 mm

CDEF

0.3 m

5.4 DESIGN OF PRISMATIC BEAMS FOR BENDING

As indicated in Sec. 5.1, the design of a beam is usually controlled by

the maximum absolute value |M|

max

of the bending moment that will

occur in the beam. The largest normal stress s

in the beam is found

at the surface of the beam in the critical section where |M|

max

occurs

and can be obtained by substituting |M|

max

for |M| in Eq. (5.1) or Eq.

(5.3).† We write

max

(5.19, 5.39)

A safe design requires that s

# s

all

, where s

all

is the allowable stress

for the material used. Substituting s

all

for s

in (5.39) and solving

for S yields the minimum allowable value of the section modulus for

the beam being designed:

min

max

(5.9)

The design of common types of beams, such as timber beams

of rectangular cross section and rolled-steel beams of various cross-

sectional shapes, will be considered in this section. A proper proce-

dure should lead to the most economical design. This means that,

among beams of the same type and the same material, and other

†For beams that are not symmetrical with respect to their neutral surface, the largest of

the distances from the neutral surface to the surfaces of the beam should be used for c

in Eq. (5.1) and in the computation of the section modulus S 5 I/c.

5.4 Design of Prismatic Beams for Bending

339

bee80288_ch05_314-379.indd Page 339 10/27/10 9:53:54 PM user-f499bee80288_ch05_314-379.indd Page 339 10/27/10 9:53:54 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

340

Analysis and Design of Beams for Bending

things being equal, the beam with the smallest weight per unit

length—and, thus, the smallest cross-sectional area—should be

selected, since this beam will be the least expensive.

The design procedure will include the following steps†:

1. First determine the value of s

all

for the material selected from

a table of properties of materials or from design specifications.

You can also compute this value by dividing the ultimate strength

of the material by an appropriate factor of safety (Sec. 1.13).

Assuming for the time being that the value of s

all

is the same

in tension and in compression, proceed as follows.

2. Draw the shear and bending-moment diagrams corresponding

to the specified loading conditions, and determine the maximum

absolute value |M|

max

of the bending moment in the beam.

3. Determine from Eq. (5.9) the minimum allowable value S

min

of the section modulus of the beam.

4. For a timber beam, the depth h of the beam, its width b, or

the ratio hyb characterizing the shape of its cross section will

probably have been specified. The unknown dimensions may

then be selected by recalling from Eq. (4.19) of Sec. 4.4 that

b and h must satisfy the relation

5 S $ S

min

5. For a rolled-steel beam, consult the appropriate table in Appen-

dix C. Of the available beam sections, consider only those with a

section modulus S $ S

min

and select from this group the section

with the smallest weight per unit length. This is the most eco-

nomical of the sections for which S $ S

min

. Note that this is not

necessarily the section with the smallest value of S (see Example

5.04). In some cases, the selection of a section may be limited by

other considerations, such as the allowable depth of the cross

section, or the allowable deflection of the beam (cf. Chap. 9).

The foregoing discussion was limited to materials for which s

all

the same in tension and in compression. If s

all

is different in tension

and in compression, you should make sure to select the beam section

in such a way that s

# s

all

for both tensile and compressive stresses.

If the cross section is not symmetric about its neutral axis, the largest

tensile and the largest compressive stresses will not necessarily occur in

the section where |M| is maximum. One may occur where M is maxi-

mum and the other where M is minimum. Thus, step 2 should include

the determination of both M

max

and M

min

, and step 3 should be modified

to take into account both tensile and compressive stresses.

Finally, keep in mind that the design procedure described in

this section takes into account only the normal stresses occurring on

the surface of the beam. Short beams, especially those made of tim-

ber, may fail in shear under a transverse loading. The determination

of shearing stresses in beams will be discussed in Chap. 6. Also, in

the case of rolled-steel beams, normal stresses larger than those con-

sidered here may occur at the junction of the web with the flanges.

This will be discussed in Chap. 8.

†We assume that all beams considered in this chapter are adequately braced to prevent

lateral buckling, and that bearing plates are provided under concentrated loads applied to

rolled-steel beams to prevent local buckling (crippling) of the web.

bee80288_ch05_314-379.indd Page 340 10/27/10 9:54:00 PM user-f499bee80288_ch05_314-379.indd Page 340 10/27/10 9:54:00 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

*Load and Resistance Factor Design. This alternative method

of design was briefly described in Sec. 1.13 and applied to mem-

bers under axial loading. It can readily be applied to the design of

beams in bending. Replacing in Eq. (1.26) the loads P

, P

, and

, respectively, by the bending moments M

, M

, and M

, we

write

1 g

# fM

(5.10)

The coefficients g

and g

are referred to as the load factors and

the coefficient f as the resistance factor. The moments M

and

are the bending moments due, respectively, to the dead and

the live loads, while M

is equal to the product of the ultimate

strength s

of the material and the section modulus S of the beam:

5 Ss

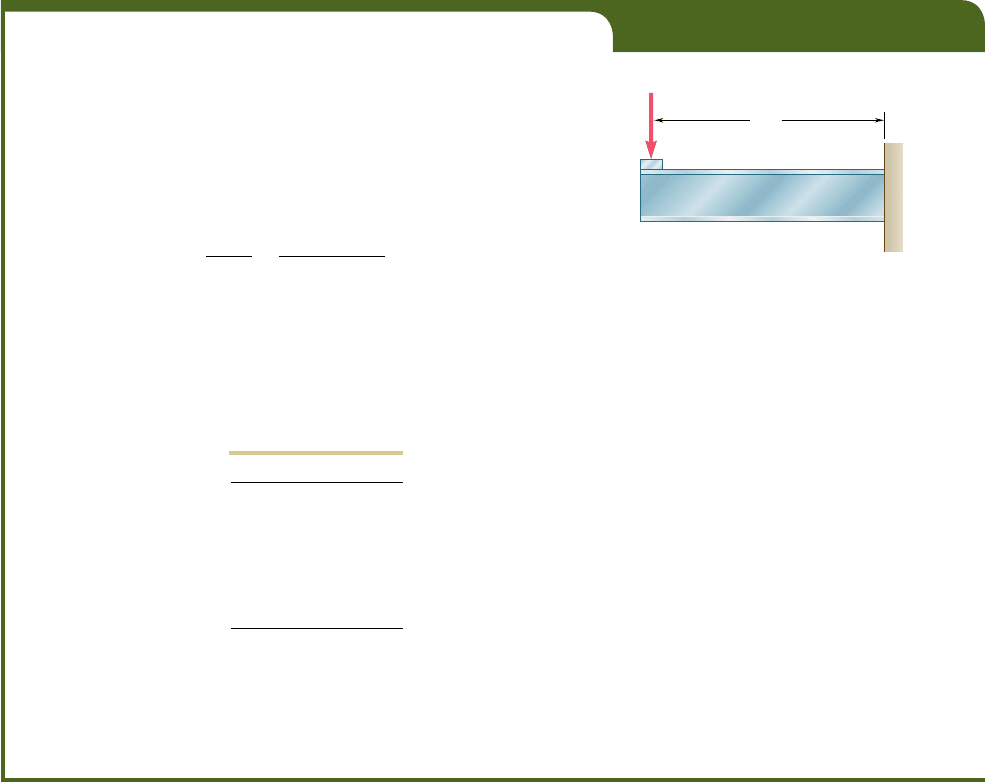
EXAMPLE 5.04

Select a wide-flange beam to support the 15-kip load as shown in Fig. 5.14.

The allowable normal stress for the steel used is 24 ksi.

1. The allowable normal stress is given: s

all

5 24 ksi.

2. The shear is constant and equal to 15 kips. The bending moment

is maximum at B. We have

ZMZ

max

15 kips

8 ft

5 120 kip ? ft 5 1440 kip ? in.

3. The minimum allowable section modulus is

min

ZMZ

max

1440

ip ? in.

24 ksi

5 60.0 in

4. Referring to the table of Properties of Rolled-Steel Shapes in Appen-

dix C, we note that the shapes are arranged in groups of the same

depth and that in each group they are listed in order of decreasing

weight. We choose in each group the lightest beam having a section

modulus S 5 Iyc at least as large as S

min

and record the results in

the following table.

Shape S, in

W21 3 44 81.6

W18 3 50 88.9

W16 3 40 64.7

W14 3 43 62.6

W12 3 50 64.2

W10 3 54 60.0

The most economical is the W16 3 40 shape since it weighs only 40 lb/ft,

even though it has a larger section modulus than two of the other shapes.

We also note that the total weight of the beam will be (8 ft) 3 (40 lb) 5

320 lb. This weight is small compared to the 15,000-1b load and can be

neglected in our analysis.

15 kips

8 ft

Fig. 5.14

341

bee80288_ch05_314-379.indd Page 341 10/27/10 9:54:00 PM user-f499bee80288_ch05_314-379.indd Page 341 10/27/10 9:54:00 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

342

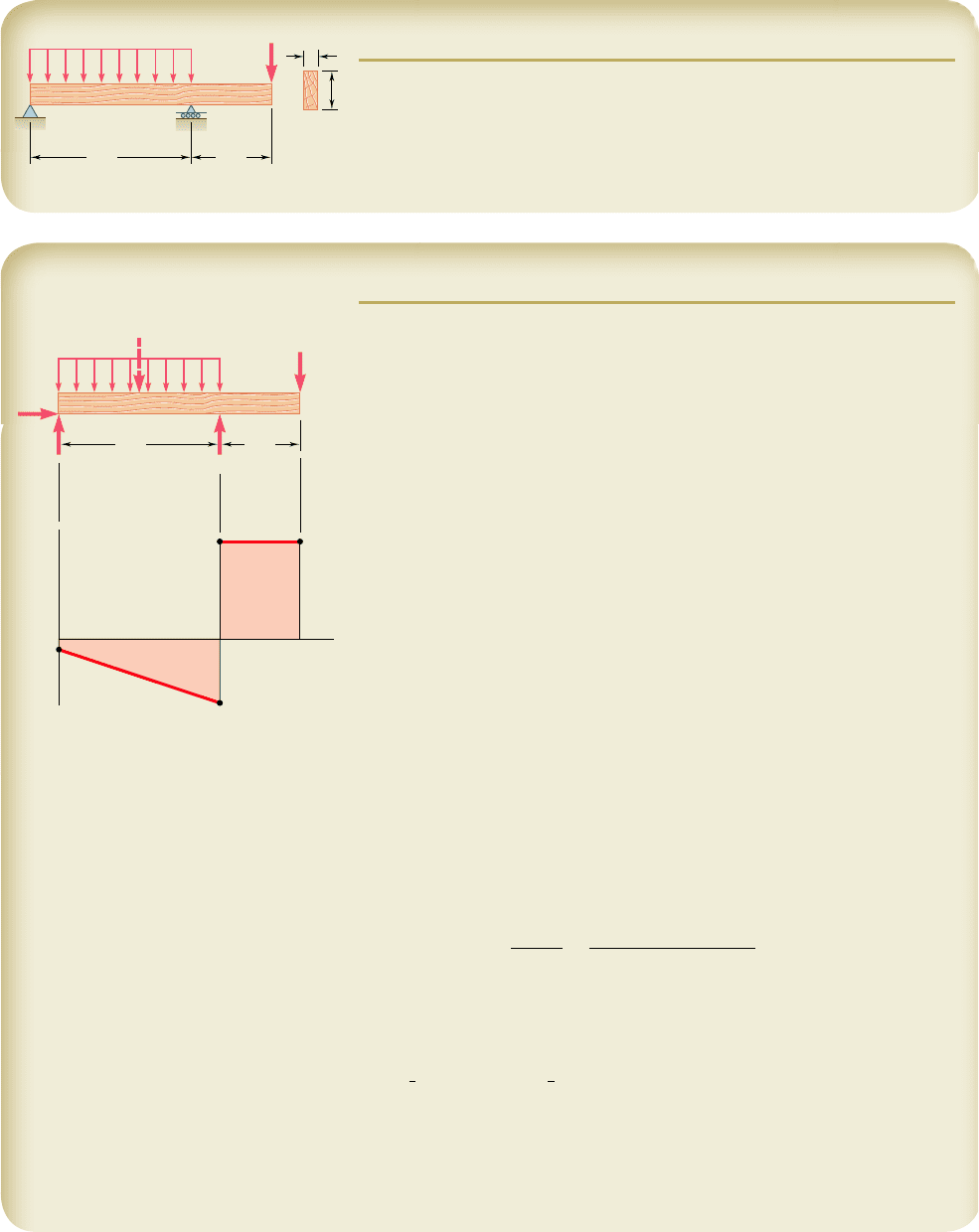
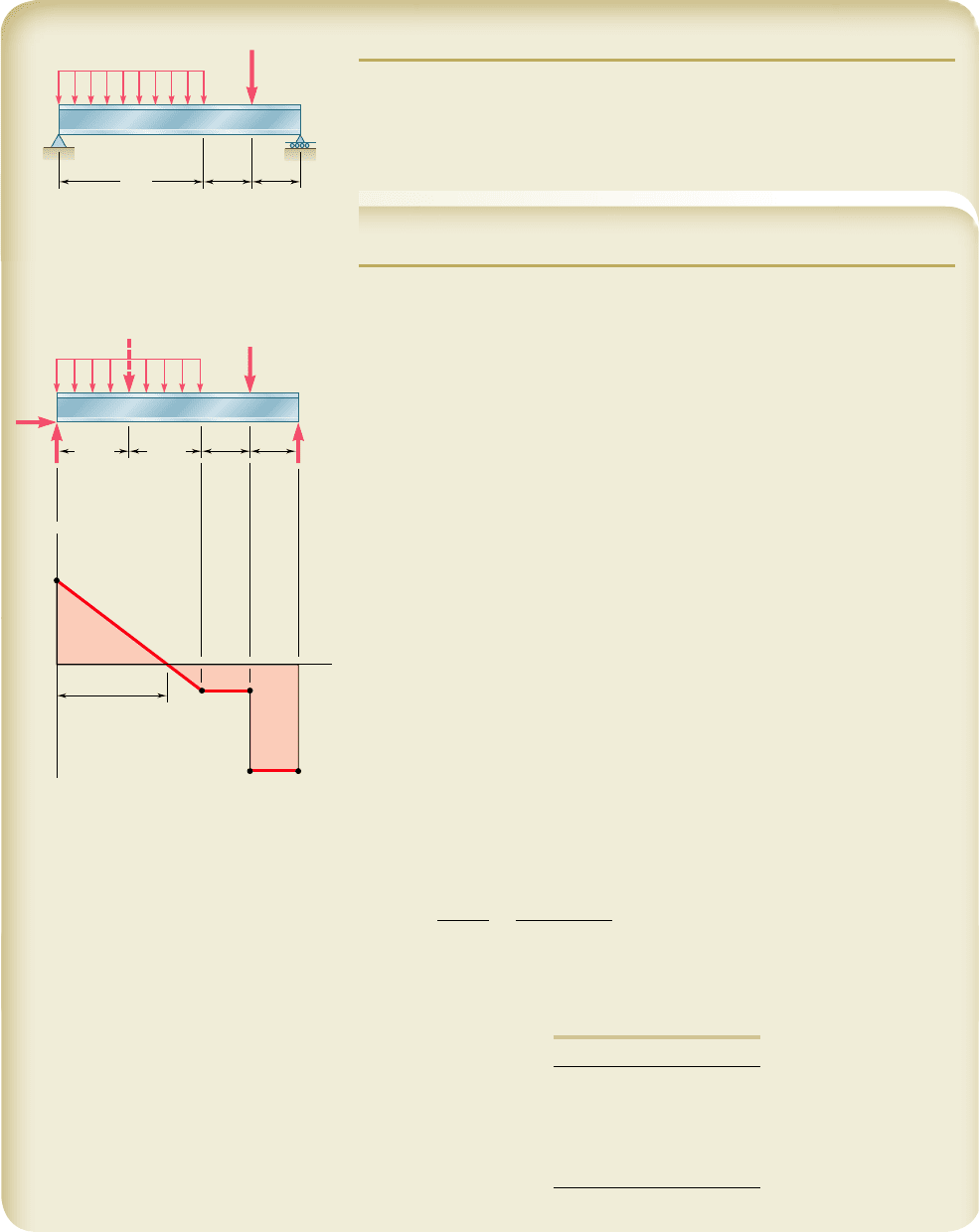
SAMPLE PROBLEM 5.7

A 12-ft-long overhanging timber beam AC with an 8-ft span AB is to be

designed to support the distributed and concentrated loads shown. Knowing

that timber of 4-in. nominal width (3.5-in. actual width) with a 1.75-ksi

allowable stress is to be used, determine the minimum required depth h of

the beam.

8 ft 4 ft

3.5 in.

400 lb/ft

4.5 kips

SOLUTION

Reactions. Considering the entire beam as a free body, we write

5 0: B18 ft22 13.2 kips214 ft22 14.5 kips2112 ft25 0

B 5 8.35 kips B 5 8.35 kipsx

5 0:

5 0

1xoF

5 0: A

1 8.35 kips 2 3.2 kips 2 4.5 kips 5 0

520.65 kips A 5 0.65 kips w

Shear Diagram. The shear just to the right of A is V

20.65 kips. Since the change in shear between A and B is equal to minus the

area under the load curve between these two points, we obtain V

by writing

2 V

521400 lb/ft218 ft2523200 lb 523.20 kips

5 V

2 3.20 kips 520.65 kips 2 3.20 kips 523.85 kips.

The reaction at B produces a sudden increase of 8.35 kips in V, resulting in a

value of the shear equal to 4.50 kips to the right of B. Since no load is applied

between B and C, the shear remains constant between these two points.

Determination of |M|

max

. We first observe that the bending moment is

equal to zero at both ends of the beam: M

5 M

5 0. Between A and B the

bending moment decreases by an amount equal to the area under the shear

curve, and between B and C it increases by a corresponding amount. Thus, the

maximum absolute value of the bending moment is |M|

max

18.00 kip ? ft.

Minimum Allowable Section Modulus. Substituting into Eq. (5.9) the

given value of s

all

and the value of |M|

max

that we have found, we write

min

0M 0

max

18 kip ? ft

12 in./ft

1.75 ksi

5 123.43 in

Minimum Required Depth of Beam. Recalling the formula developed

in part 4 of the design procedure described in Sec. 5.4 and substituting the

values of b and S

min

, we have

$ S

min



13.5 in.2h

$ 123.43 in

h $ 14.546 in.

The minimum required depth of the beam is

5 14.55 in.

◀

Note: In practice, standard wood shapes are specified by nominal dimensions that

are slightly larger than actual. In this case, we would specify a 4-in. 3 16-in. member,

whose actual dimensions are 3.5 in. 3 15.25 in.

8 ft 4 ft

3.2 kips

4.5 kips

(⫺18)

(⫹18)

4.50

kips

⫺3.85 kips

⫺0.65

kips

bee80288_ch05_314-379.indd Page 342 11/16/10 6:42:31 PM user-f499bee80288_ch05_314-379.indd Page 342 11/16/10 6:42:31 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

343

SAMPLE PROBLEM 5.8

A 5-m-long, simply supported steel beam AD is to carry the distributed and

concentrated loads shown. Knowing that the allowable normal stress for the

grade of steel to be used is 160 MPa, select the wide-flange shape that

should be used.

SOLUTION

Reactions. Considering the entire beam as a free body, we write

1loM

5 0: D15 m22 160 kN211.5 m22 150 kN214 m25 0

D 5 58

0 kN D 5 58.0 kNx

5 0: A

5 0

1xoF

5 0: A

1 58.0 kN 2 60 kN 2 50 kN 5 0

5 52.0 kN A 5 52.0 kNx

Shear Diagram. The shear just to the right of A is V

152.0 kN. Since the change in shear between A and B is equal to minus

the area under the load curve between these two points, we have

5 52.0 kN 2 60 kN 528 kN

The shear remains constant between B and C, where it drops to 258 kN,

and keeps this value between C and D. We locate the section E of the beam

where V 5 0 by writing

2 V

52wx

0 2 52.0 kN 52120 kN/m2

Solving for x we find x 5 2.60 m.

Determination of |M|

max

. The bending moment is maximum at E,

where V 5 0. Since M is zero at the support A, its maximum value at E is

equal to the area under the shear curve between A and E. We have, there-

fore, |M|

max

5 67.6 kN ? m.

Minimum Allowable Section Modulus. Substituting into Eq. (5.9) the

given value of s

all

and the value of |M|

max

that we have found, we write

min

max

67.6 kN ? m

160 MPa

5 422.5 3 10

Selection of Wide-Flange Shape. From Appendix C we compile a

list of shapes that have a section modulus larger than S

min

and are also the

lightest shape in a given depth group.

Shape S, mm

W410 3 38.8 629

W360 3 32.9 475

W310 3 38.7 547

W250 3 44.8 531

W200 3 46.1 451

We select the lightest shape available, namely W360 3 32.9b

1.5 m

52 kN

x ⫽ 2.6 m

⫺58 kN

⫺8 kN

(67.6)

1.5 m

1 m 1 m

50 kN

EB C D

60 kN

3 m

1 m 1 m

20 kN

50 kN

bee80288_ch05_314-379.indd Page 343 10/28/10 7:26:00 PM user-f499bee80288_ch05_314-379.indd Page 343 10/28/10 7:26:00 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

PROBLEMS

344

5.65 and 5.66 For the beam and loading shown, design the cross

section of the beam, knowing that the grade of timber used has an

allowable normal stress of 12 MPa.

5.67 and 5.68 For the beam and loading shown, design the cross

section of the beam, knowing that the grade of timber used has an

allowable normal stress of 1750 psi.

5.69 and 5.70 For the beam and loading shown, design the cross

section of the beam, knowing that the grade of timber used has an

allowable normal stress of 12 MPa.

1.8 kN 3.6 kN

0.8 m 0.8 m 0.8 m

40 mm

Fig. P5.65

1.2 m 1.2 m

125 mm

18 kN/m

Fig. P5.66

1.2 kips/ft

6 ft

Fig. P5.68

3 ft

6 ft

5 in.

1.5 kips/ft

3 ft

Fig. P5.67

150 mm

3 kN/m

2.4 m 1.2 m

Fig. P5.70

0.6 m 0.6 m

3 m

100 mm

6 kN/m

2.5 kN2.5 kN

Fig. P5.69

bee80288_ch05_314-379.indd Page 344 10/27/10 9:54:16 PM user-f499bee80288_ch05_314-379.indd Page 344 10/27/10 9:54:16 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

345

ProblemsProblems

5.71 and 5.72 Knowing that the allowable stress for the steel used

is 24 ksi, select the most economical wide-flange beam to support

the loading shown.

Fig. P5.72

2.75 kips/ft

24 kips

9 ft 15 ft

5 ft

12 ft

5 ft

62 kips

Fig. P5.71

5.73 and 5.74 Knowing that the allowable stress for the steel used

is 160 MPa, select the most economical wide-flange beam to sup-

port the loading shown.

Fig. P5.73

6 kN/m

18 kN/m

6 m

Fig. P5.74

5 kN/m

70 kN 70 kN

3 m 3 m

5 m

5.75 and 5.76 Knowing that the allowable stress for the steel used

is 160 MPa, select the most economical S-shape beam to support

the loading shown.

Fig. P5.75

2.5 m 2.5 m 5 m

60 kN 40 kN

Fig. P5.76

45 kN/m

3 m 3 m

9 m

70 kN 70 kN

5.77 and 5.78 Knowing that the allowable stress for the steel used

is 24 ksi, select the most economical S-shape beam to support the

loading shown.

48 kips 48 kips 48 kips

6 ft

2 ft2 ft

2 ft

Fig. P5.77

3 kips/ft

18 kips

DCB

6 ft 6 ft

3 ft

Fig. P5.78

bee80288_ch05_314-379.indd Page 345 10/27/10 9:54:31 PM user-f499bee80288_ch05_314-379.indd Page 345 10/27/10 9:54:31 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

346

Analysis and Design of Beams for Bending

5.79 Two L102 3 76 rolled-steel angles are bolted together and used

to support the loading shown. Knowing that the allowable normal

stress for the steel used is 140 MPa, determine the minimum angle

thickness that can be used.

4.5 kN/m

9 kN

1 m1 m

152 mm

102 mm

Fig. P5.79

5.80 Two rolled-steel channels are to be welded back to back and used

to support the loading shown. Knowing that the allowable normal

stress for the steel used is 30 ksi, determine the most economical

channels that can be used.

5.81 Three steel plates are welded together to form the beam shown.

Knowing that the allowable normal stress for the steel used is

22 ksi, determine the minimum flange width b that can be used.

2.25 kips/ft

20 kips

12 ft

3 ft

6 ft

Fig. P5.80

8 kips 32 kips 32 kips

4.5 ft

14 ft

9.5 ft

in.

1 in.

19 in.

Fig. P5.81

5.82 A steel pipe of 100-mm diameter is to support the loading shown.

Knowing that the stock of pipes available has thicknesses varying

from 6 mm to 24 mm in 3-mm increments, and that the allowable

normal stress for the steel used is 150 MPa, determine the mini-

mum wall thickness t that can be used.

5.83 Assuming the upward reaction of the ground to be uniformly dis-

tributed and knowing that the allowable normal stress for the steel

used is 24 ksi, select the most economical wide-flange beam to

support the loading shown.

BCD

100 mm

1.5 kN 1.5 kN

1 m

0.5 m 0.5 m

1.5 kN

Fig. P5.82

200 kips 200 kips

4 ft

4 ft 4 ft

Fig. P5.83

Total load  2 MN

0.75 m 0.75 m

1 m

Fig. P5.84

5.84 Assuming the upward reaction of the ground to be uniformly dis-

tributed and knowing that the allowable normal stress for the steel

used is 170 MPa, select the most economical wide-flange beam to

support the loading shown.

bee80288_ch05_314-379.indd Page 346 10/27/10 9:54:49 PM user-f499bee80288_ch05_314-379.indd Page 346 10/27/10 9:54:49 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles