Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

CHAPTER

437

Transformations of

Stress and Strain

bee80288_ch07_436-511.indd Page 437 10/30/10 1:36:46 AM user-f499bee80288_ch07_436-511.indd Page 437 10/30/10 1:36:46 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

438

Chapter 7 Transformations of

Stress and Strain

7.1 Introduction

7.2 Transformation of Plane Stress

7.3 Principal Stresses; Maximum

Shearing Stress

7.4 Mohr’s Circle for Plane Stress

7.5 General State of Stress

7.6 Application of Mohr’s Circle to

the Three-Dimensional Analysis

of Stress

*7.7 Yield Criteria for Ductile

Materials under Plane Stress

*7.8 Fracture Criteria for Brittle

Materials under Plane Stress

7.9 Stresses in Thin-Walled Pressure

Vessels

*7.10 Transformation of Plane Strain

*7.11 Mohr’s Circle for Plane Strain

*7.12 Three-Dimensional Analysis of

Strain

*7.13 Measurements of Strain; Strain

Rosette

7.1 INTRODUCTION

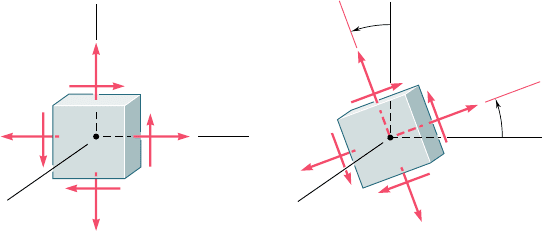
We saw in Sec. 1.12 that the most general state of stress at a given

point Q may be represented by six components. Three of these com-

ponents, s

, s

, and s

, define the normal stresses exerted on the faces

of a small cubic element centered at Q and of the same orientation as

the coordinate axes (Fig. 7.1a), and the other three, t

, t

, and t

,†

the components of the shearing stresses on the same element. As we

remarked at the time, the same state of stress will be represented by

a different set of components if the coordinate axes are rotated

(Fig. 7.1b). We propose in the first part of this chapter to determine

how the components of stress are transformed under a rotation of the

coordinate axes. The second part of the chapter will be devoted to a

similar analysis of the transformation of the components of strain.

Our discussion of the transformation of stress will deal mainly

with plane stress, i.e., with a situation in which two of the faces of

the cubic element are free of any stress. If the z axis is chosen per-

pendicular to these faces, we have s

5 t

5 0, and the only

remaining stress components are s

, s

, and t

(Fig. 7.2). Such a

situation occurs in a thin plate subjected to forces acting in the mid-

plane of the plate (Fig. 7.3). It also occurs on the free surface of a

structural element or machine component, i.e., at any point of the

surface of that element or component that is not subjected to an

external force (Fig. 7.4).

†We recall that t

5 t

, t

5 t

, and t

5 t







y'z'



y'x'



x'z'



z'x'



z'y'



x'y'



(a)

(b)



Fig. 7.1 General state of stress at a point.





Fig. 7.2 Plane stress.

Fig. 7.3 Example of plane stress.

Fig. 7.4 Example of plane stress.

bee80288_ch07_436-511.indd Page 438 10/30/10 1:36:52 AM user-f499bee80288_ch07_436-511.indd Page 438 10/30/10 1:36:52 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

439

7.1 Introduction



x'y'



z'  z



(a)(b)

Fig. 7.5 Transformation of stress.

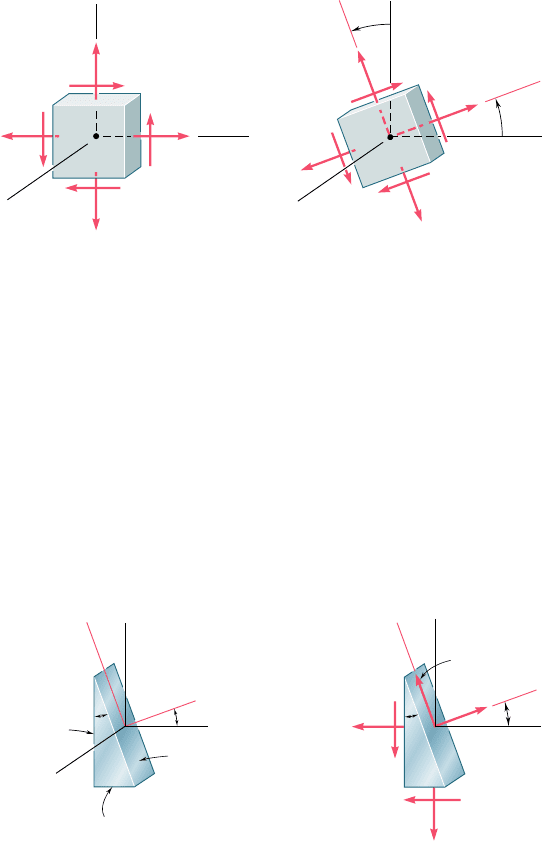
Considering in Sec. 7.2 a state of plane stress at a given point

Q characterized by the stress components s

, s

, and t

associated

with the element shown in Fig. 7.5a, you will learn to determine the

components s

, s

, and t

x9y9

associated with that element after it

has been rotated through an angle u about the z axis (Fig. 7.5b). In

Sec. 7.3, you will determine the value u

of u for which the stresses

and s

are, respectively, maximum and minimum; these values

of the normal stress are the principal stresses at point Q, and the

faces of the corresponding element define the principal planes of

stress at that point. You will also determine the value u

of the angle

of rotation for which the shearing stress is maximum, as well as the

value of that stress.

In Sec. 7.4, an alternative method for the solution of problems

involving the transformation of plane stress, based on the use of

Mohr’s circle, will be presented.

In Sec. 7.5, the three-dimensional state of stress at a given point

will be considered and a formula for the determination of the normal

stress on a plane of arbitrary orientation at that point will be devel-

oped. In Sec. 7.6, you will consider the rotations of a cubic element

about each of the principal axes of stress and note that the corre-

sponding transformations of stress can be described by three differ-

ent Mohr’s circles. You will also observe that, in the case of a state

of plane stress at a given point, the maximum value of the shearing

stress obtained earlier by considering rotations in the plane of stress

does not necessarily represent the maximum shearing stress at that

point. This will bring you to distinguish between in-plane and out-

of-plane maximum shearing stresses.

Yield criteria for ductile materials under plane stress will be

developed in Sec. 7.7. To predict whether a material will yield at

some critical point under given loading conditions, you will deter-

mine the principal stresses s

and s

at that point and check whether

, s

, and the yield strength s

of the material satisfy some crite-

rion. Two criteria in common use are: the maximum-shearing-strength

criterion and the maximum-distortion-energy criterion. In Sec. 7.8,

fracture criteria for brittle materials under plane stress will be devel-

oped in a similar fashion; they will involve the principal stresses s

and s

at some critical point and the ultimate strength s

of the

bee80288_ch07_436-511.indd Page 439 10/30/10 1:37:04 AM user-f499bee80288_ch07_436-511.indd Page 439 10/30/10 1:37:04 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

440

Transformations of Stress and Strain

material. Two criteria will be discussed: the maximum-normal-stress

criterion and Mohr’s criterion.

Thin-walled pressure vessels provide an important application

of the analysis of plane stress. In Sec. 7.9, we will discuss stresses in

both cylindrical and spherical pressure vessels (Photos 7.1 and 7.2).

Photo 7.1

Cylindrical

pressure vessel.

Photo 7.2 Spherical pressure vessel.

Sections 7.10 and 7.11 will be devoted to a discussion of the

transformation of plane strain and to Mohr’s circle for plane strain.

In Sec. 7.12, we will consider the three-dimensional analysis of strain

and see how Mohr’s circles can be used to determine the maximum

shearing strain at a given point. Two particular cases are of special

interest and should not be confused: the case of plane strain and the

case of plane stress.

Finally, in Sec. 7.13, we discuss the use of strain gages to mea-

sure the normal strain on the surface of a structural element or

machine component. You will see how the components P

, P

, and

characterizing the state of strain at a given point can be computed

from the measurements made with three strain gages forming a

strain rosette.

7.2 TRANSFORMATION OF PLANE STRESS

Let us assume that a state of plane stress exists at point Q (with s

5 t

5 0), and that it is defined by the stress components s

, and t

associated with the element shown in Fig. 7.5a. We pro-

pose to determine the stress components s

, s

, and t

x9y9

associated

with the element after it has been rotated through an angle u about

bee80288_ch07_436-511.indd Page 440 10/30/10 7:30:35 PM user-f499bee80288_ch07_436-511.indd Page 440 10/30/10 7:30:35 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

441

the z axis (Fig. 7.5b), and to express these components in terms of

, s

, t

, and u.

In order to determine the normal stress s

and the shearing

stress t

x9y9

exerted on the face perpendicular to the x9 axis, we con-

sider a prismatic element with faces respectively perpendicular to

the x, y, and x9 axes (Fig. 7.6a). We observe that, if the area of the

7.2 Transformation of Plane Stress



x'y'



z'  z



(a)(b)

Fig. 7.5 (repeated)

(a)

A cos



A sin



A

(b)

(A cos )



(A cos )





x'y'

A



(A sin )







A



(A sin )





Fig. 7.6

oblique face is denoted by DA, the areas of the vertical and horizon-

tal faces are respectively equal to DA cos u and DA sin u. It follows

that the forces exerted on the three faces are as shown in Fig. 7.6b.

(No forces are exerted on the triangular faces of the element, since

the corresponding normal and shearing stresses have all been assumed

equal to zero.) Using components along the x9 and y9 axes, we write

the following equilibrium equations:

x¿

5 0:s

x¿

¢A 2 s

¢A cos u

cos u 2 t

¢A cos u

sin u

¢A sin u

sin u 2 t

¢A sin u

cos u 5 0

5 0:t

x¿

¢A 1 s

¢A cos u

sin u 2 t

¢A cos u

cos u

¢A sin u

cos u 1 t

¢A sin u

sin u 5 0

bee80288_ch07_436-511.indd Page 441 10/30/10 1:37:09 AM user-f499bee80288_ch07_436-511.indd Page 441 10/30/10 1:37:09 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

442

Transformations of Stress and Strain

Solving the first equation for s

and the second for t

x9y9

, we have

x¿

5 s

cos

u 1 s

sin

u 1 2t

sin u cos u (7.1)

x¿y¿

521s

2 s

2 sin u cos u 1 t

1cos

u 2 sin

u2 (7.2)

Recalling the trigonometric relations

sin 2u 5 2 sin u cos u

cos 2u 5 cos

u 2 sin

u (7.3)

and

cos

u 5

1 1 cos 2u

sin

u 5

1 2 cos 2u

(7.4)

we write Eq. (7.1) as follows:

x¿

5 s

1 1 cos 2u

1 s

1 2 cos 2u

1 t

sin 2u

x¿

1 s

2 s

cos 2u 1 t

sin 2u

(7.5)

Using the relations (7.3), we write Eq. (7.2) as

x¿y¿

sin 2u 1 t

cos 2u

(7.6)

The expression for the normal stress s

is obtained by replacing u in

Eq. (7.5) by the angle u 1 908 that the y9 axis forms with the x axis.

Since cos (2u 1 1808) 5 2cos 2u and sin (2u 1 1808) 5 2sin 2u, we

have

y¿

1 s

2 s

cos 2u 2 t

sin 2u

(7.7)

Adding Eqs. (7.5) and (7.7) member to member, we obtain

x¿

1 s

y¿

5 s

1 s

(7.8)

Since s

5 s

5 0, we thus verify in the case of plane stress that

the sum of the normal stresses exerted on a cubic element of mate-

rial is independent of the orientation of that element.†

†Cf. first footnote on page 97.

bee80288_ch07_436-511.indd Page 442 11/17/10 11:10:19 PM user-f499bee80288_ch07_436-511.indd Page 442 11/17/10 11:10:19 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

443

7.3 PRINCIPAL STRESSES; MAXIMUM

SHEARING STRESS

The equations (7.5) and (7.6) obtained in the preceding section are

the parametric equations of a circle. This means that, if we choose

a set of rectangular axes and plot a point M of abscissa s

and ordi-

nate t

x9y9

for any given value of the parameter u, all the points thus

obtained will lie on a circle. To establish this property we eliminate

u from Eqs. (7.5) and (7.6); this is done by first transposing (s

1 s

)/2

in Eq. (7.5) and squaring both members of the equation, then squar-

ing both members of Eq. (7.6), and finally adding member to mem-

ber the two equations obtained in this fashion. We have

x¿

1 s

1 t

x¿y¿

5 a

2 s

1 t

(7.9)

Setting

ave

1 s

and

R 5

2 s

1 t

(7.10)

we write the identity (7.9) in the form

x¿

2 s

ave

1 t

x¿y¿

5 R

(7.11)

which is the equation of a circle of radius R centered at the point C

of abscissa s

ave

and ordinate 0 (Fig. 7.7). It can be observed that,

due to the symmetry of the circle about the horizontal axis, the same

result would have been obtained if, instead of plotting M, we had

plotted a point N of abscissa s

and ordinate 2t

x9y9

(Fig. 7.8). This

property will be used in Sec. 7.4.

7.3 Principal Stresses; Maximum

Shearing Stress



x'y'



x'y'





ave

Fig. 7.8 Equivalent formation of stress

transformation circle.

Fig. 7.7 Circular relationship of

transformed stresses.



x'y'



x'y'



min



max



ave

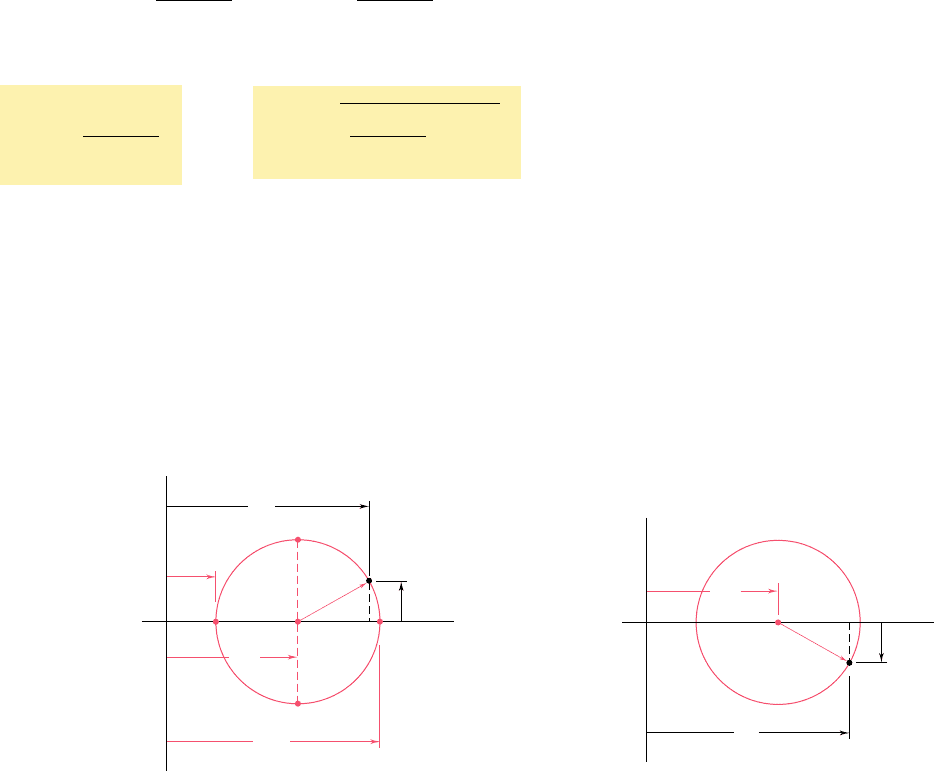
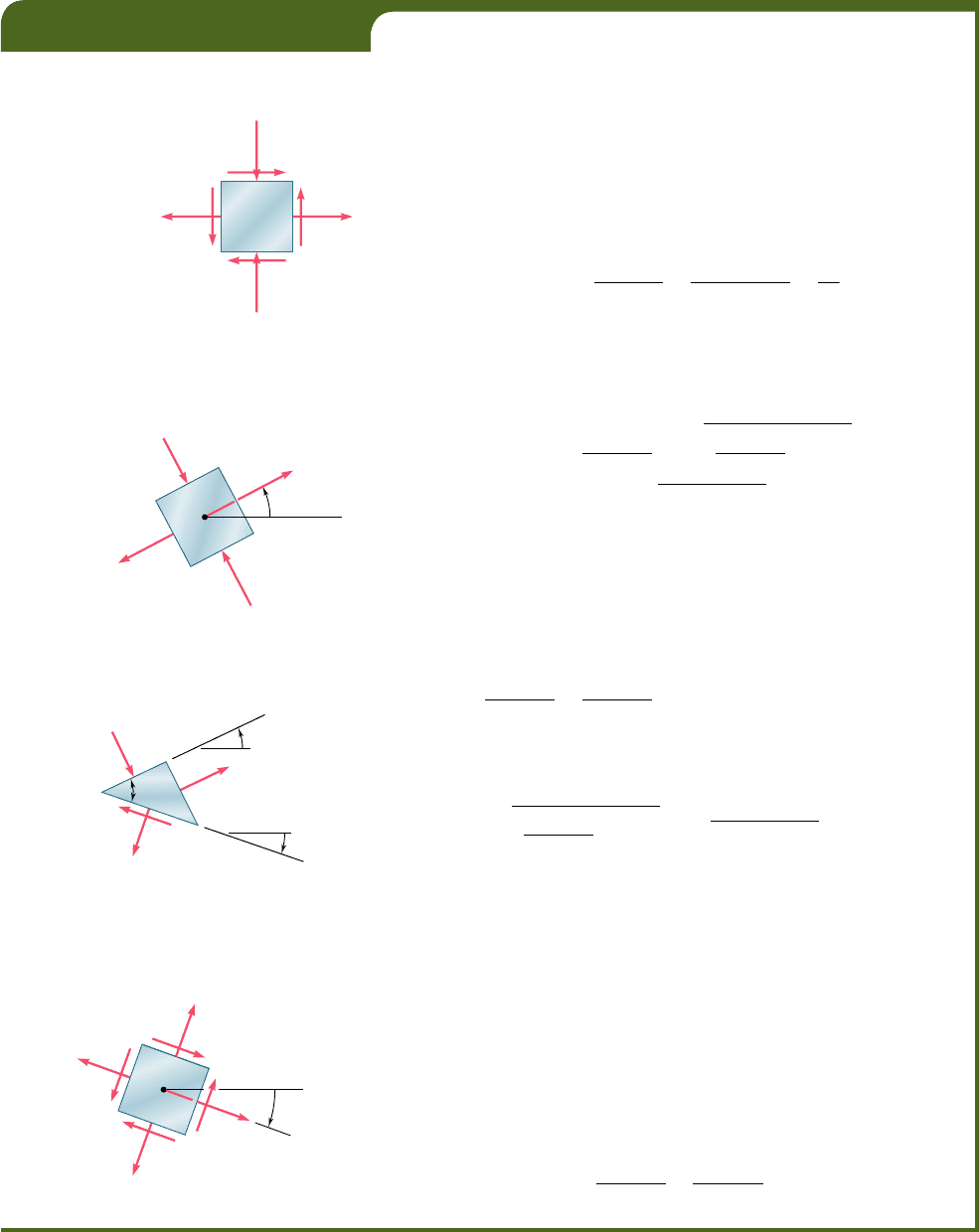
The two points A and B where the circle of Fig. 7.7 intersects

the horizontal axis are of special interest: Point A corresponds to the

maximum value of the normal stress s

, while point B corresponds

bee80288_ch07_436-511.indd Page 443 11/17/10 11:10:21 PM user-f499bee80288_ch07_436-511.indd Page 443 11/17/10 11:10:21 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

444

Transformations of Stress and Strain

to its minimum value. Besides, both points correspond to a zero

value of the shearing stress t

x9y9

. Thus, the values u

of the parameter

u which correspond to points A and B can be obtained by setting

x9y9

5 0 in Eq. (7.6). We write†

tan 2u

2 s

(7.12)

This equation defines two values 2u

that are 1808 apart, and thus

two values u

that are 908 apart. Either of these values can be used

to determine the orientation of the corresponding element (Fig. 7.9).

†This relation can also be obtained by differentiating s

in Eq. (7.5) and setting the

derivative equal to zero: ds

ydu 5 0.



min



min



max



max



Fig. 7.9 Principal stresses.

The planes containing the faces of the element obtained in this way

are called the principal planes of stress at point Q, and the corre-

sponding values s

max

and s

min

of the normal stress exerted on these

planes are called the principal stresses at Q. Since the two values u

defined by Eq. (7.12) were obtained by setting t

x9y9

5 0 in Eq. (7.6),

it is clear that no shearing stress is exerted on the principal planes.

We observe from Fig. 7.7 that

max

5 s

ave

1 Rands

5 s

ave

2 R (7.13)

Substituting for s

ave

and R from Eq. (7.10), we write

max, min

1 s

2 s

1 t

(7.14)

Unless it is possible to tell by inspection which of the two principal

planes is subjected to s

max

and which is subjected to s

min

, it is neces-

sary to substitute one of the values u

into Eq. (7.5) in order to

determine which of the two corresponds to the maximum value of

the normal stress.

Referring again to the circle of Fig. 7.7, we note that the points

D and E located on the vertical diameter of the circle correspond to

bee80288_ch07_436-511.indd Page 444 10/30/10 1:37:19 AM user-f499bee80288_ch07_436-511.indd Page 444 10/30/10 1:37:19 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

445

the largest numerical value of the shearing stress t

x9y9

. Since the abscissa

of points D and E is s

ave

5 (s

1 s

)y2, the values u

of the param-

eter u corresponding to these points are obtained by setting s

1 s

)y2 in Eq. (7.5). It follows that the sum of the last two terms

in that equation must be zero. Thus, for u 5 u

, we write†

2 s

cos 2u

1 t

sin 2u

5 0

tan 2u

2 s

(7.15)

This equation defines two values 2u

that are 1808 apart, and thus

two values u

that are 908 apart. Either of these values can be used

to determine the orientation of the element corresponding to the

maximum shearing stress (Fig. 7.10). Observing from Fig. 7.7 that

the maximum value of the shearing stress is equal to the radius R of

the circle, and recalling the second of Eqs. (7.10), we write

max

2 s

1 t

(7.16)

As observed earlier, the normal stress corresponding to the condition

of maximum shearing stress is

s¿ 5 s

ave

1 s

(7.17)

Comparing Eqs. (7.12) and (7.15), we note that tan 2u

the negative reciprocal of tan 2u

. This means that the angles 2u

and 2u

are 908 apart and, therefore, that the angles u

and u

are 458 apart. We thus conclude that the planes of maximum shear-

ing stress are at 458 to the principal planes. This confirms the

results obtained earlier in Sec. 1.12 in the case of a centric axial

loading (Fig. 1.38) and in Sec. 3.4 in the case of a torsional loading

(Fig. 3.19.)

We should be aware that our analysis of the transformation of

plane stress has been limited to rotations in the plane of stress. If

the cubic element of Fig. 7.5 is rotated about an axis other than the

z axis, its faces may be subjected to shearing stresses larger than the

stress defined by Eq. (7.16). As you will see in Sec. 7.5, this occurs

when the principal stresses defined by Eq. (7.14) have the same sign,

i.e., when they are either both tensile or both compressive. In such

cases, the value given by Eq. (7.16) is referred to as the maximum

in-plane shearing stress.

†This relation may also be obtained by differentiating t

x9y9

in Eq. (7.6) and setting the

derivative equal to zero: dt

x9y9

ydu 5 0.



max



max







Fig. 7.10 Maximum shearing

stress.

7.3 Principal Stresses; Maximum

Shearing Stress

bee80288_ch07_436-511.indd Page 445 11/17/10 11:10:26 PM user-f499bee80288_ch07_436-511.indd Page 445 11/17/10 11:10:26 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07

Apago PDF Enhancer

446

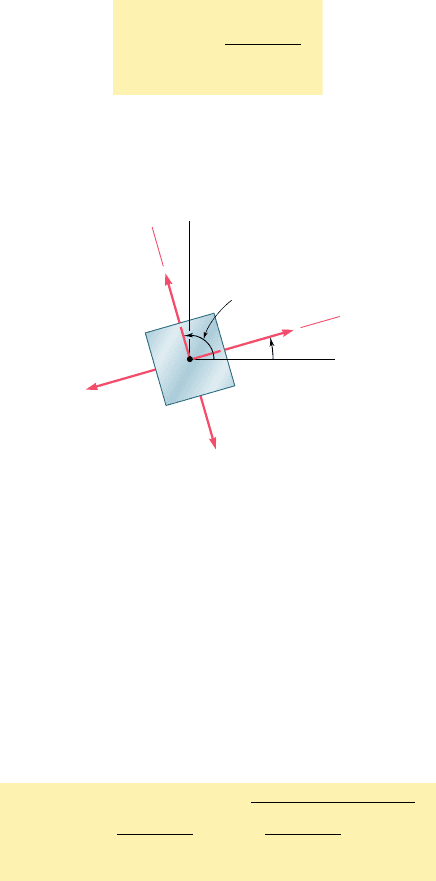
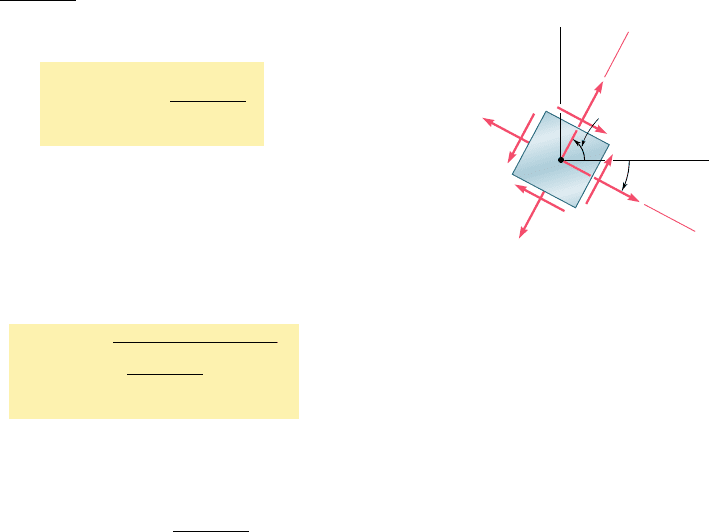
For the state of plane stress shown in Fig. 7.11, determine (a) the prin-

cipal planes, (b) the principal stresses, (c) the maximum shearing stress

and the corresponding normal stress.

(a) Principal Planes. Following the usual sign convention, we

write the stress components as

5150 MPas

5210 MPat

5140 MPa

Substituting into Eq. (7.12), we have

tan 2u

2 s

21140

50 2 12102

2 u

5 53.1°and180° 1 53.1° 5 233.1°

5 26.6°and116.6°

(b) Principal Stresses. Formula (7.14) yields

max, min

1 s

2 s

1 t

5 20 6 21302

1 1402

5 20 1 50 5 70 MPa

min

5 20 2 50 5230 MPa

The principal planes and principal stresses are sketched in Fig. 7.12. Mak-

ing u 5 26.68 in Eq. (7.5), we check that the normal stress exerted on

face BC of the element is the maximum stress:

x¿

50 2 1

50 1 10

cos 53.1° 1 40 sin 53.1°

5 20 1 30 cos 53.1° 1 40 sin 53.1° 5 70 MPa 5 s

max

2 s

1 t

5 21302

1 1402

5 50 MPa

Since s

max

and s

min

have opposite signs, the value obtained for t

max

actually represents the maximum value of the shearing stress at the point

considered. The orientation of the planes of maximum shearing stress and

the sense of the shearing stresses are best determined by passing a section

along the diagonal plane AC of the element of Fig. 7.12. Since the faces

AB and BC of the element are contained in the principal planes, the

diagonal plane AC must be one of the planes of maximum shearing stress

(Fig. 7.13). Furthermore, the equilibrium conditions for the prismatic

element ABC require that the shearing stress exerted on AC be directed

as shown. The cubic element corresponding to the maximum shearing

stress is shown in Fig. 7.14. The normal stress on each of the four faces

of the element is given by Eq. (7.17):

s¿ 5 s

ave

1 s

50 2 10

5 20 MPa

EXAMPLE 7.01

10 MPa

40 MPa

50 MP

Fig. 7.11



min

 30 MPa



max

 70 MP



 26.6

Fig. 7.12



min



max



max



 26.6



 45

45

18.4

Fig. 7.13





max



 18.4

 20 MPa



 20 MPa

 50 MPa

Fig. 7.14

bee80288_ch07_436-511.indd Page 446 10/30/10 1:37:25 AM user-f499bee80288_ch07_436-511.indd Page 446 10/30/10 1:37:25 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07