Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

Chapter33 • Lines and Planes in Space

203

Thesinglevectorequation

above

equivalent

to the threeparametric equations

x=xo+tf

y=yo+tm

z=zo+tn.

Here the parameter t can be thought of as time, with R(t)

giving

the positionof a point at

time

Non-parallel lines in space do not necessarily intersect, but we define the angle be-

tween any two lines

to be the anglethatwouldbe

formed

if the lineswere

moved

parallelto

themselves

so they did intersect. A line's orientation in spaceis determined by the

angles

makes

with the coordinate

axes.

Let A = ai + bj + ck be a unit vectorparallel to someline,

andpictureA withits tail at the

origin.

Let a,

{3,

)' be the

angles

A makeswiththe

axes,

and

hencealso be

angles

the line

makes

withthe

axes.

SinceA andi, j, k areunit

vectors,

A·i = a =

IIAllllil1

cos a = cos a,

A · j = b = cos

{3,

A · k =c =cos )'.

The

numbers

a, b,c, or cos a, cos

{3,

cos

1',

are calledthe direction cosines of the line.

Since

A is a unit

vector,

= 1, so for any direction cosines,

cos-

a +cos'

+cos- )' = 1.

Any

numbers

f, m,n whichare proportional to cos a, cos

{3,

cos )' are calleddirection num-

bers

of the line. In the plane the orientation of a line is determined by a

single

number,

the

slope.

In three-space werequire three

numbers,

direction

numbers,

determine

thedirection

ofa

line.

EXAMPLE

33.1

Find a vectorrepresentation and a parametricrepresentation for the linethrough

= (1,2, 3) and par-

allel to A = 4i -

j +2k. Givethe directioncosinesof the line.

Solution

A vector representation is

R(t) =

+ tA

= (i + 2j + 3k) + t(4i - j + 2k)

= (1 + 4t) i + (2 - t) j + (3 + 2t) k.

The equivalent parametricrepresentation is

x = 1 + 4t

y=2-t

z = 3 + 2t.

For each real number t the point (1 + 4t, 2 - t, 3 + 2t) lies on the line, and conversely every point on

the line corresponds to some

t. We can also think of R(t) as giving the position of a point at time t

as the point moves along the line. The numbers 4, -1, 2 are the direction numbers of the line. Since

IIAII

v'4

+ 1

+ 2

= V2I, A/V2I is a unit vector,and

cosa=

V2I

are directioncosinesof the line.

-1

cos f3=

V2I

cos

V2I

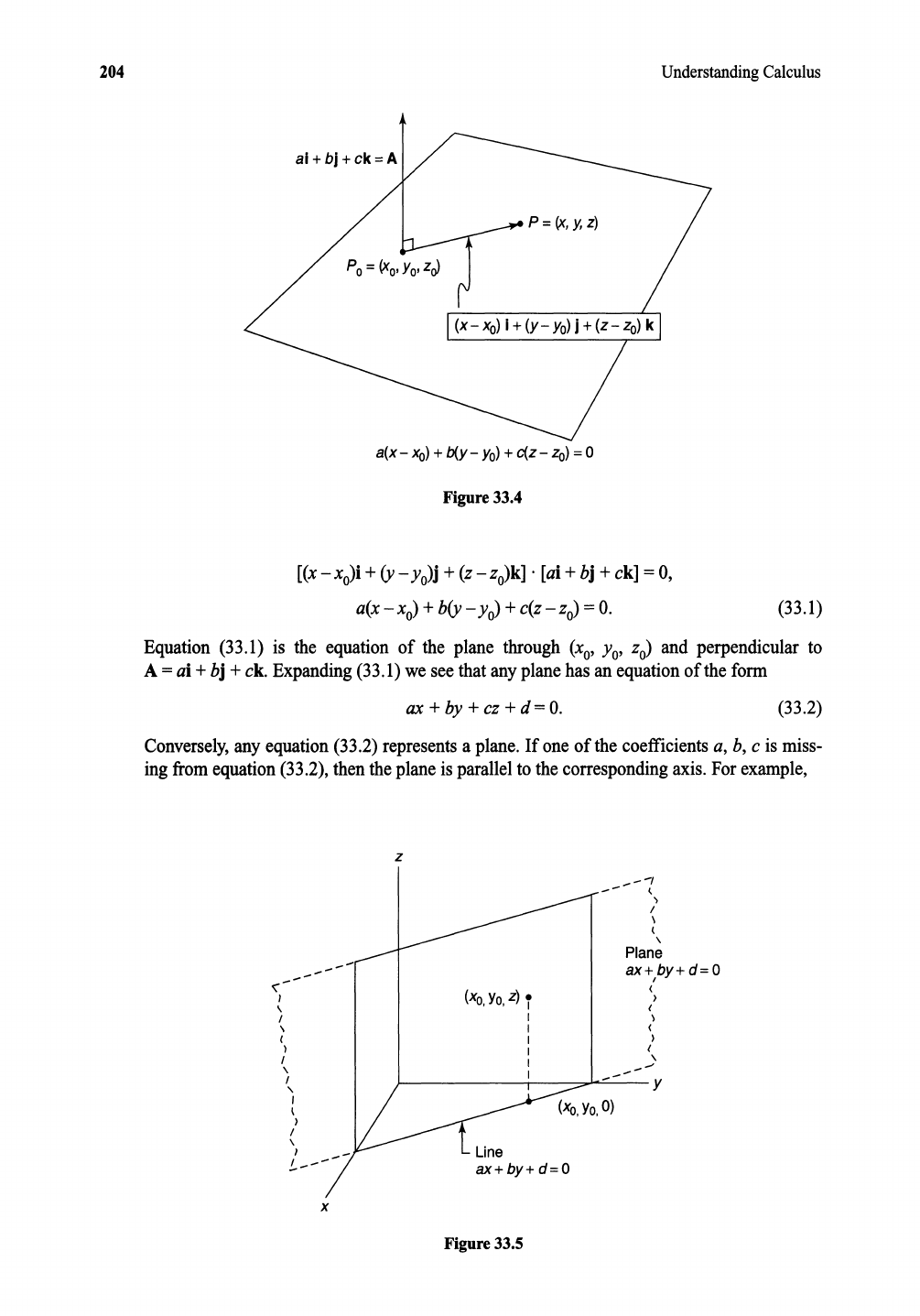
The orientation of a plane in space is determined by a vector perpendicular to the

plane.

= (x

Yo'

zo)

is anypointin a plane,

an~

= ai +bj + ck is perpendicular to the

plane,then for anypoint

P =(x, y, z) on the plane P

. A =

(Figure

33.4).

Thatis,

204

Understanding

Calculus

al + bj +

ck=A

P =

(x,

a(x-

xo)

b(y-

Yo)

c(z-

zo)

= 0

Figure 33.4

[(x

-xo)i

+(v- yo)j +(z

-zo)k]

. [ai +bj +ck] = 0,

a(x- x

+bty -

Yo)

+c(z-

zo)

(33.1)

Equation

(33.1) is the

equation

of the plane

through

Yo'

zo)

and perpendicular to

= ai +bj +ck.

Expanding

(33.1) weseethatanyplanehasan

equation

of the form

ax + by +cz +

(33.2)

Conversely,

any

equation

(33.2)

represents

plane.

If one of the coefficients a, b, c is

miss-

ing

from

equation

(33.2), thentheplaneis parallel to the

corresponding

axis.

For

example,

---,

-- {

(

Plane

ax +,by +

d=O

(

)

(

)

(

....."

Line

ax+

by+

d=O

(xo,

Yo,

z) T

~--------r---~--y

(

)

1----

----

Figure 33.5

Chapter

33 • Linesand

Planes

Space

ax+by+d=O

205

(33.3)

is theplane

which

is parallel to the

z-axis

andgoes

through

thelinein the

xy-plane

which

has

this

equation.

If (x

Yo,

0) satisfies

(33.3),

then (x

Yo,

z) satisfies

(33.3)

for any

number

(Figure

33.5).

EXAMPLE

33.2

Writethe

equation

of the plane

which

is perpendicular to A = 2i - j +3k and

passes

through

the point

(3,2, 5).

Where

doestheplane

intersect

the

x-axis?

Solution

From(33.1) the

equation

2(x- 3) - (y - 2) +3(z - 5) = 0,

2x-y+3z-19=0.

Tofind the

intersection

withthe

x-axis

puty =z =°andfindx =

19/2.

EXAMPLE

33.3

Graph

thepart of theplane3x+2y +6z =6 inthefirst

octant.

Solution

Sincethe intersection of two

planes

is a line,the

given

planewill

intersect

the three

coordinate

planes

in three

different

lines.

determine

theselinesit suffices to find the points

where

the

given

planein-

tersects

the

coordinate

axes.

If y =z = 0, then x = 2, so (2, 0, 0) is on the

graph.

Similarly,

putting

x =z =Owegety =3, so

(0,3,0)

is onthe

graph.

Ifx =y =0, thenz = 1,so (0, 0, 1)isonthe

graph.

The

intercepts

are (2, 0, 0), (0, 3, 0), and(0,0, 1),andthe graphis

shown

Figure

33.6.

3x+Sz=S

_-----lI_

3x+2y+Sz=S

2y+ SZ= S

-+--------+-----+-----~--y

z=O,3x+2y=S

Figure 33.6

206

Understanding

Calculus

Ourfinalvectoroperation is calledthe cross product and is

denoted

A x B. The cross

product

vectors

A andB is a

vector

perpendicular to bothA andB, withlength

IIA

BII

IIAII

IIBllsin

where

8 is the

angle

between

A and B. The vectorA x B

points

in the direction a righthand

screw

would

move

if A

were

rotated into B

through

the

smallest

possible

angle.

(Figure

33.7).

If A andB areparallel, A x B is the zero

vector.

AxB

Right

angles

(33.4)

Figure 33.7

Fromthe definition it

follows

that

A=-A

x B,

andfor

every

scalarc,

(cA) x B = A x (cB) = c(A x B).

originally setup our

coordinate

system

so thex,y, z

axes

forma right-handed sys-

tem as

shown

Figure

33.1.

Thatis, so thati x j = k. In this

system

have

the

following

relations:

i x j = k j x k = i k x i =

j x i =

-k

k x j =

-i

i x k =

-j.

i x i = j x j = k x k = O.

Thecrossproduct satisfies the

distributive

law:

A x (B + C) = A x B + A x C.

canuse

(33.4)

and

(33.5)

compute

A x B forany

vectors

A andB written in termsofi,

j, andk. If A =

ali

+ a

j + a

k andB = bli + b

j + b

k, then

A x B =

(ali

+ a

j + a

k) x (bli + b

j + b

albli

x i +a

x j +a

x k

j x i +a

j x j +a

2bJ

x k

k x i +a

k x j +a

k x k.

Thethreetermsi x l, j x j, andk x k arezero,so

x B = (a

)

i - (a

j +(a

- a

(33.6)

The easywayto

remember

the

formula

(33.6)

is to writethe crossproduct as a 3 x 3

determinant.

Recall

that2 x 2

determinants

are definedas

follows:

a21

= a

- a

•

hI h

Three

by three

determinants

are

given

(33.7)

Chapter33 • Lines and Planes in Space

x y z

a\ a

=Xl:~

::I-yl::

::I+ZI::

:~I

=x(a

) -

y(a

)

+z(a

) ·

If we replacex, y, z by i, j, k, then (33.8)is the formulafor A x B:

i j k

A x B = a

EXAMPLE

33.4

(a) Evaluatethe 3 x 3 determinant

123

4 -1

5·

706

(b) Find the crossproduct of A =4i - j +5k and B =7i +6k.

Solution

(a) Using (33.8)and (33.9)we get

1 2 3

~ -~

=1'1-~

:1-2'1~

:1+3'1~

-~I

= (1)(-6 - 0) - (2)(24 - 35) +(3)(0 +7)

=(1)(-6) - (2)(-11) + (3)(7) =37.

(b) The coefficientsof i, j, k in A x B are the 2 x 2 determinants of part (a), so

207

(33.8)

(33.9)

AxB=

4 -1

7 0

=-6i

Ilj

+7k.

EXAMPLE

33.5

Findthe equationof the plane throughP = (1, 1, 1), Q = (5, 2, 1), R = (3, 4, 0).

Solution

Once we have a normal vector A = ai + bj + ck, then we can write the equationusing anyone of the

points

R; i.e.,

a(x - 1) +b(y - 1)+c(z - 1)= 0,

a(x - 5) +b(y - 2) +c(z- 1)= 0,

a(x - 3) + b(y - 4) + cz =

Since

and

fiR

lie in the plane,

fiR

is a normal

vector.

(33.10)

(33.11)

(33.12)

PQ=4i

+ j

fiR

= 2i +

3j-k

208

Understanding Calculus

--7~-------~--------

d=llpollcos(}

=po-A/IIAII

Figure 33.8

PQxPR=

4 2

2 3

o =

-i

+4j + 10k,

-1

and using (33.10)the equationof the plane is

-{x-I)

4(y-1)

10(z-1)

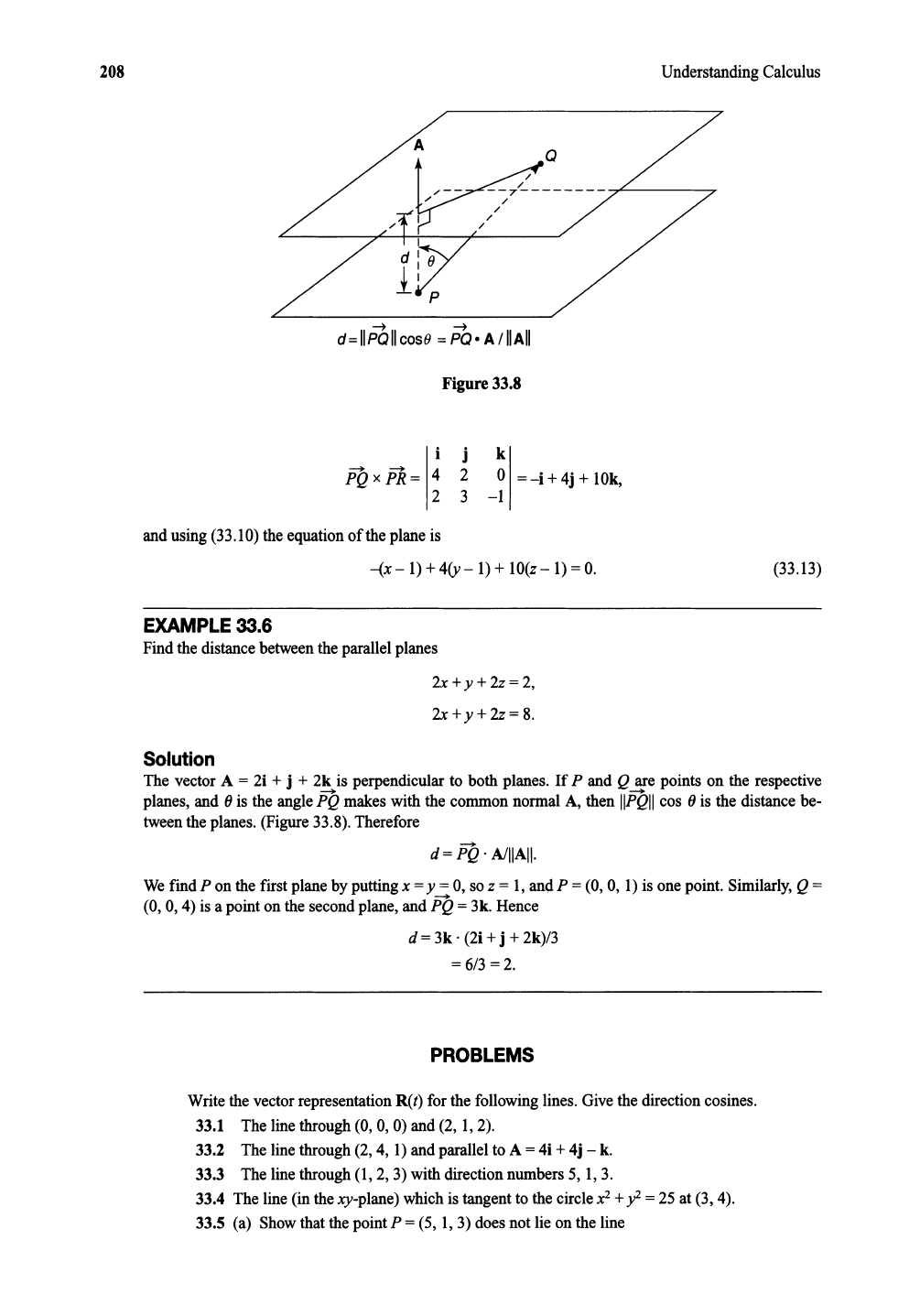
EXAMPLE

33.6

Findthe distancebetweenthe parallelplanes

2x +

2z=

2x +

2z=

(33.13)

Solution

The vector A = 2i + j + 2k is perpendicularto both planes.

P and Q are points on the respective

planes, and (J is the angle

fiQ

makes with the commonnormal A, then I

IfiQl

Icos (J is the distance be-

tweenthe planes. (Figure

33.8). Therefore

d =

fiQ

A/IIAII.

Wefind P on the first plane by puttingx =y = 0, so z = 1, and P = (0,0, 1) is one point. Similarly, Q =

(0,0,4)

is a point on the secondplane, and

fiQ

= 3k. Hence

d = 3k . (2i + j + 2k)/3

= 6/3 = 2.

PROBLEMS

Writethe vectorrepresentation R(t) for the following lines.Givethe directioncosines.

33.1 The line through(0, 0, 0) and (2, 1, 2).

33.2 The line through(2, 4, 1) and parallelto A

= 4i + 4j - k.

33.3 The line through(1, 2, 3) with directionnumbers5, 1, 3.

33.4 The line (in the xy-plane) whichis tangentto the circle

= 25 at (3, 4).

33.5 (a) Showthat the point

P = (5, 1, 3) does not lie on the line

B = 3i +2j - 5k.

= 2i +3j.

B=i+j+k.

B = 3i +5j - 4k.

Chapter33 • Linesand Planesin Space

R(t) = (5- t)i + (4 + 3t)j + (1- t)k.

(b) Findthe point Qon the line suchthat

is perpendicular to the line.

d fromP = (5, 1, 3) to the line.

Findthe anglebetweenthe

following

lines.

33.6 R

(t) = (1 + t) i + (2 - t) j + (2 + 2t) k;

~(t)

= (1 + t) i + (2 + 2t) j + (2- 2t) k.

33.7

R1(t)= t i +2t j +3t k;

~(t)

= (1 + 2t) i + (2 + 3t)j + (3 - 2t) k.

Findthe equationof the plane described.

33.8 Through

(1,2,3)

andperpendicular to A =i - j +2k.

33.9 Through(2, 0, 1)and perpendicular to A

= 2i + 3j - k.

33.10 Through(0, 0, 0) and perpendicular to A

= j.

33.11 Through(0,0, 1) and perpendicular to A =

-i

+j.

Findthe crossproductsA x B.

33.12

A = i - 2j +k

33.13 A = 4i +j +k

33.14

A=i-k

33.15 A = 7i - 2j +3k

Findthe equationof the plane.

33.16 Through(2, 1, 3), (4, 2, -1), (5, 1, 1).

33.17 Through(1,0, 5), (2,2, 3), (-1, 1,0).

33.18 Through(1, 1, 1),(2, 1,0), (0, 1,3).

Findthe distancebetweenthe parallelplanes.

33.19 4x + 2y + 4z = 6 4x + 2y + 4z = 24.

33.20

x-2y+z=2

x-2y+z=5.

33.21 3x - y +2z = 2 6x- 2y +4z = 8.

Findthe distancefrom the point to the plane.

33.22

P=(3,0,

2x-y+4z=2.

33.23

P=(1,0,3)

3x-2y+z=7.

33.24 Showthat if A = ali + a

j + a

k, B = bli + b

j + b

k, C =

cli

+ c2i + c

k, then

209

33.25 (a) Showthat

IIA

BII

is the area of the parallelogram whosesidesare A and

(b) Showthat IC . A x BI is the volumeof the parallelepiped with A, B, C at one comer.

Surfaces

started our study of plane curves by looking at the graphs of lines, parabolas, ellipses,

and hyperbolas. Thesecurvesare calledconicsectionsbecausethey can all be realizedas the

intersection of a plane and a cone.The equations of the conics

involve

onlythe first and sec-

ond

powers

of the variables x andy. Tostart our studyof surfacesin three spacewewill look

at a few standard surfaces which

involve

only the first and second

powers

of x, y, and z.

Thesesurfaces, exceptfor the planes, are calledquadric surfaces.

In the plane all linear equations ax + by + C = 0 representlines, and in three spaceall

linearequations

Ax+By+Cz+D=O

(34.1)

represent planes. The orientation of the plane (34.1) is determined by the

normal vector

+ Bj + Ck.

After the planes, the next simplest surfaces are the spheres. The sphere centered at

Yo,

zo)has the equation

(x - X

+ (y -

YO)2

+ (z -

ZO)2

i2,

(34.2)

wherer is the radius of the

sphere.

The left side of (34.2) is the square of the distancefrom

(x,y, z) to (x

YO'

zo)' so (34.2)is the condition thatpoints(x,y, z) be a constantdistancefrom

Yo,

zo)·

By expanding the terms in (34.2)we see that everyspherehas an equationof the form

+r + z2+Ax + By + Cz + D =

(34.3)

An equationof the form (34.3)need not haveany graph (e.g.,x

+r +

+ 1 = 0), or may

havea singlepoint as its graph (e.g.,

+r +

= 0).

However,

if (34.3)does havea proper

graph,thenthe graphis a

sphere.

One seesthisby completing the squares, whichgivesus the

coordinates of the center, and the radius.

211

212

Understanding Calculus

EXAMPLE

34.1

Findthe centerandradiusof the sphere

+Z2 - 2x +4z - 4 =

Solution

Complete

the squares as

follows

by adding1to thex-termsand 4 to thez-terms:

2x + 1) +

+(Z2 +4z +4) - 4 = 5,

(x -

1)2

+(z +

2)2

= 9.

The centeris (1, 0, -2) andthe radiusis 3.

know

thatin the

xy-plane

thegraphof ax +by+d = 0 is a

line.

However,

if wecon-

siderthisan

equation

inx, y, andz, thenthegraphis a planeparallel to the

z-axis.

In the same

waywe can

consider

the graphof

to be the unit circlein the

xy-plane,

or as the cylinder

consisting

of all points (x, y, z) such

that

(x,y, 0) liesonthe

circle.

(Figure

34.1).

will more

generally

refer to the three

dimensional

graph of any equation of the

form

F(x,y) = 0 or F(x,z) = 0, or F(y,z) = 0 as a cylindrical

surface.

The

surface

consists of

all lines

which

pass

through

the planecurveand are perpendicular to the plane of the

curve.

For

example,

Figure

34.2

shows

the parabolic cylinder

consisting

of all the lines

which

are

parallel to the

x-axis

and pass

through

the parabola y = Z2 in the

yz-plane.

The graph of any

equation in

two

variables

is a cylindrical

surface

3-space.

Surfaces

revolution

areparticularly easyto

identify,

andeasyto

graph.

Consider the

surface

(Figure

34.3)

(34.4)

In anyplanez =constant (z

0), the cross

section

of the

surface

is a circlecentered at thez-

axis.

Hence

the

surface

is a

surface

of revolution aboutthe

z-axis.

The fact thatz is a

func-

tionofx

is whatidentifies this as a

surface

revolution.

Thetraceof the

surface

in the

xz-plane

(i.e., with y = 0) is the parabola z = x

and the trace in the

yz-plane

is the same

(x,y,z)

Cylinder

I I

-t;L_

....

/ I I "

---j~-----~-------y

Figure 34.1

Chapter 34 •

Surfaces

~-I'---+~

....a....-

---a...

Parabolic

cylinder

Figure 34.2

Paraboloid

revolution

Figure 34.3

213

parabola rotated through 90° to

z = y. The surface is generated by rotating either

these

parabolas about the z-axis. This surface is called a

paraboloid

of revolution. (Figure 34.3.)

The surfaces

y = x

+z2 and x =y +Z2 have the same shape, only with different axes. For ex-

ample, the y-axis is the axis for

y = x

+ Z2.