Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

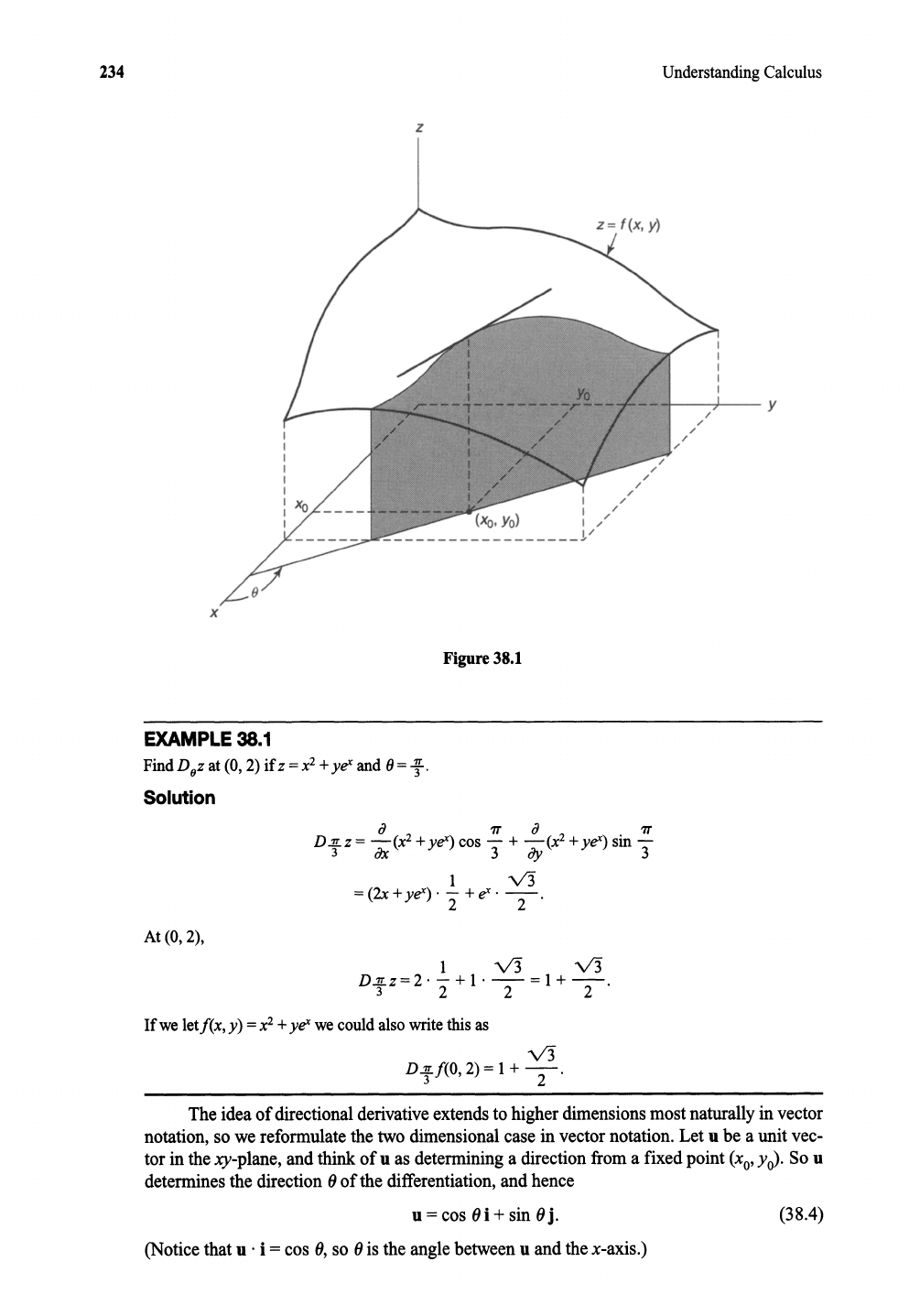
234

Understanding Calculus

-I--

--}-

- - Y

(.>co

. Yo) I /

____

_ _ _ _ _ _ _ _ _

_____

Figure

38.1

EXAMPLE

38.1

FindDoz at (0,2) ifz

+ye" and 8=f .

Solution

a 7T a 7T

D.JLZ

-(x

ye<)

cos - +

-(Xl

ye<)

sin-

3 dx 3

1 V3

=(2x +

ye<)

+ e' .

-2-

At (0, 2),

1 V3

v'3

z = 2 .

+ I .

-2-

= I +

-2-

Ifwe

letf(x,y)

+ye' wecouldalso write this as

v'3

Dff(O

, 2) =1+

-2-

The ideaof directional

derivative

extends to higherdimensions mostnaturally in vector

notation, so wereformulate the two dimensional casein vectornotation. Let u be a unit vec-

tor in the

xy-plane,

andthinkof u as determining a direction froma fixedpoint

(XO'

Yo)'

So u

determines the direction

of the differentiation, and hence

= cos 9

sin 9 j.

(Notice that u . i = cos 9,so

is the anglebetween u andthe x-axis.)

(38.4)

Chapter38 • Gradient andDirectional

Derivatives

235

definea vector

function

Vf(x, y) (read"delf(x,

y)")

follows:

Vf(x, y) =

fx(x,

y) i +!;(x, y) j.

(38.5)

The vector

function

Vf(x, y) is calledthe gradient

off

(x, y). If u is the unit vector

(38.4)

the direction 8,then

D(Jf(x,y) =

Vf(x,y)·

ifx(x,

y) i +

J;,(x,

· (cos 8 i +sin 8

h(x,y)

cos

J;,(x,y)sin 8.

(38.6)

If the direction is givenby a unit vectoru then

Vf·

u is the directional

derivative

in that di-

rection.

alsowrite

Duffor

Jwhen

u =cos 8i +sin 8j.

EXAMPLE

38.2

Findthedirectional

derivative

off(x,

y) = 2x - Y+3xyin the direction

ofv

= 3i - 4j, at the point(1, 3).

Solution

Welet u =

~j,

so u is a unitvectorin the direction ofv. The gradient

off(x,

y) is

a a

Vf(x,y) =

-(2x

- Y+ 3xy)i+

-(2x

- Y+ 3xy)j

= (2 + 3y)i + (-2y + 3x)j.

At (1,3) wehave

Vf(I, 3) =

IIi

- 3j,

3 4

1,3) . u =

(11

i - 3j) . (

i -

33 12 45

=-+-=-=9

5 5 5 .

Fromthe vectorform

Vf·

u it is clearwhatdirection u mustbe to get the

maximum

di-

rectional

derivative.

Since

Vf·

u =

IIVfllcos

8,u mustbe parallel to Vjfor the

derivative

to be

maximum,

andthe

maximum

derivative

isjust

IIV

ill. The gradient Vf is a vector which points

in the direction

the maximum directional derivative, and its magnitude

IIVill

is the maxi-

mum directional derivative.

If you think of z =f(x, y) as the surface of a hill, and you are standing on the hill at

Yo,

zo),

thenVf(x

' yo)

is a horizontal vector-like a

compass

direction-which pointsin

the steepest uphill

direction.

The two horizontal

vectors

perpendicular to Vf(x

Yo)

will be

tangent to the levelcurve

f(x, y) = c,

where

c =

f(x

Yo).

EXAMPLE

38.3

The surfaceof a mountain has the equationz = 10- 2x

+2xy- y, wherex, y, and z are measured in

thousands of feet.

You

are standing on the mountainside at x = 2,y = 3, z = 5, and youwantto climbas

fastas possible. Whatdirection (i.e.,what

compass

heading) do yougo, andhowsteepwillbe the slope

in that direction?

Solution

The

maximum

directional

derivative

is in the direction of Vf

Vf(x, y) = (-4x +2y) i +(2x - 2y) j,

236

Understanding Calculus

Vf(2, 3)

= (-8 +6) i +(4- 6) j =

-2i

- 2j.

The gradient says head southwest for the steepest slope, and the steepest slope will be

IIVf(2,

3)11

2V2.

Sincea slope

of2V2

2.8 is prettysteep,you mightthendecideto go aroundthe mountainin-

steadof up overit.

In that casev=2i - 2j is tangentto the levelcurveat (2, 3), since

Vf(2,

3) . (2i - 2j) =(-2i - 2j) . (2i- 2j) =

You

shouldhead southeastfor a levelpath.

EXAMPLE

38.4

Find a vector T tangent to the curve

xy2

+ x

y =

-6

at (2,

-1)

and a vector N normal to the curve at

(2, -1).

Solution

Wecan considerthe curveas a levelcurveof the surfacez =

xy2

y so Vz(2,

-1)

willbe normalto the

curve.

(y2

+3x

y) i +(2xy+x

)

At (2, -1), Vz=

-IIi

+ 4j and this vectorwillbe normalto the curveat (2,-1). The vector

-4i

- l l] (or

4i + l lj) will be tangentto the curve at the point.

Fora

function

of three

variables,

w =

f(x,

y, z), the gradient is the vectordefinedby

Vf(x,y,

z) =

Ixi

j +h

If u = ai + bj +ck is a unit

vector

thenthe line

through

Yo,

zo)

in the direction u is

given

parametrically by

x=xo+as

y=yo+bs

z=zo+cs,

(38.7)

where

s is the

distance

from(x

Yo,zo)'It

follows

fromthe chainrule that

dw=awdx+Bwdy+Bwdz

aw aw aw

=-a+-b+-c

Vf'

u. (38.8)

Thedirectional

derivative

of a

function

of three

variables

is againthe dotproduct of Vf and a

unit

vector

in the specified

direction.

EXAMPLE

38.5

The temperature in a certainthree dimensional regionis givenby

T(x,

y, z) = x

y + yz + Z2.

A sensormovesthroughthe regionand its velocityat the point (2, 1, 3) is v = 2i - 2j + k. At whatrate

is the temperature at the sensorchangingas it passesthrough(2, 1, 3)?

Solution

dT dT

Whatwe wanthere is at,wheret is time.Weknowthat

iIS=

VT'

u whereu =

v/llvll.

Since

dT dT ds

-=-.-

dt ds dt

Chapter 38 • Gradientand DirectionalDerivatives

and Qi =

Ilvll,

we have

dT ( v )

dt = VT·"jj;jj

IIvll

=VT·

Wecalculate VTat (2, 1, 3):

VT=

Vt(x

+ yz +

Z2)

= 3x

i +(x

+z) j + (y +2z) k.

VT(2, 1, 3) = I2i +

IIj

+ 7k.

Finally,

=VT·v

(I2i

IIj

+7k) . (2i - 2j + k)

= 24 - 22 + 7 = 9,

and the temperatureis changingat 9 degreesper second.

PROBLEMS

237

6=-j.

FindD(J

f(x

Yo)

for the following functions.

38.1 f(x, y) =xer +

sin(xy)

Yo)

(~,

0) 6 =

38.2 f(x, y) =

2.xy3-

- 1 (x

Yo)

= (1, 2) 6 =

38.3 f(x, y) = x

xy2

Yo)

= (1, 2) 6 = 11'.

38.4 f(x, y) =x tanY + log(1 + x

Yo)

=(1, 0)

38.5

f(x,y)

=cos

+ sin

(xo'Yo)

(~,

38.6 f(x, y) = sinh(x+ y) (x

Yo)

= (0, 0)

38.7

f(x,y)

= sin-Ix+ secy (x

Yo)

= (0, D

38.8

f(X,y)=~2+y2

Yo)

=(0,

Find the derivative in the directionv at the givenpoint.

38.9

f(x,y)

= 3x - 2y +x

V = 2i +j (x

Yo)

= (3, 1).

38.10 f(x, y) =

+ x

V =

-i

+ 3j (x

Yo)

= (-1, 1).

38.11 f(x, y) = tan-Ix + tan(x

+ r) v = 5i - j (x

Yo)

= (0, 0).

38.12 f(x, y) =

sinh(xy)

v =3i - 4j (x

Yo)

= (2, 4).

38.13 f(x, y, z) = x

V = i - j +2k (x

Yo'

zo)= (1, 2, 3).

38.14

f(x,y,

log(I +x

+yz V = 3i - 4k (x

Yo'

zo)= (1,0,2).

Find a vectorN normal to the givencurve and a vector T tangent to the curve at the givenpoint.

38.15

xer

+xy = 1 at (1,0).

38.16 tanx +

= 9 at

(~,

2).

38.17 log(x

+r)+ xy = 2 at (e, 0).

38.18 x

coshy

+ y cosh x = 1 at (1, 0).

38.19 If

T(x,y, z) = x +

+xz is the temperatureof a particle at (x, y, z), and v = i - j + 2k is

the velocity of the particle, what is

at (2, 0, 1),where t is time?

Maxima and Minima

Tofind the relativemaximumand minimumvaluesof a functionf(x) of one variable we first

find all the criticalpoints

suchthatf'(xo) =

The conditionf'(x

)

=0 is necessaryforf(x)

to havea max or min at x

but not a sufficientcondition. For example,

iff(x)

thenf'(O)

= 0 butf(O) is neither a maximumnor a minimum. To get a sufficient conditionwe use the

second derivative.

Iff'(xo)

=0, thenf(xo) is a relative minimum

iff"(xo)

> 0 andf(xo) is a

relativemaximum

iff"(xo)

For a functionf(x, y) of two variables the geometry is a little more complicated. The

critical points as usual are the points

Yo)

where the first derivatives are zero:!x(x

Yo)

!;(x

Yo)

If both first partials are zero at (x

Yo)'

then the surfacez =f(x, y) has a hori-

zontaltangentplane at

Yo),

and this is a necessaryconditionfor a relativemax or min, but

not a sufficient condition. Considerthe saddleshaped surface

z =

f(x,y)

=2x

- r

(39.1)

shownin Figure 39.1. Here we have the single critical point (0, 0),

andfxx(O,

0) = 4 > 0 and

fyy(O,

0) =

-2

The curvez = 2x

in the xz-plane has a relativeminimumat x = 0, and the

curve

z =

-r

in the yz-plane has a relative maximum at y =

Clearlyf(x, y) has neither a

maximumnor a minimumat (0, 0).

It is clear from the example(39.1)that

bothfxx andfyymust havethe same sign at a crit-

ical point

iff

(x, y) is to havea relativeextremepoint there.This is indeed a necessarycondi-

tion, but still not a sufficientcondition. Considerthe function

f(x, y) = 2(x - y)2- (x +y)2

6xy+

(39.2)

The surfacez = f(x, y) is saddleshaped like the surfaceof Figure39.1, onlyrotated45° about

the z-axis. For the function(39.2),(0, 0) is the only criticalpoint,

andfxx(O,

0) =

2,f

yy(0,

0) =

2. However,f(x, y) does not havea relativeminimumat (0, 0) as the secondderivatives sug-

gest, since on the line

y = x the function is -(2x)2, which has a relative maximum at (0, 0).

239

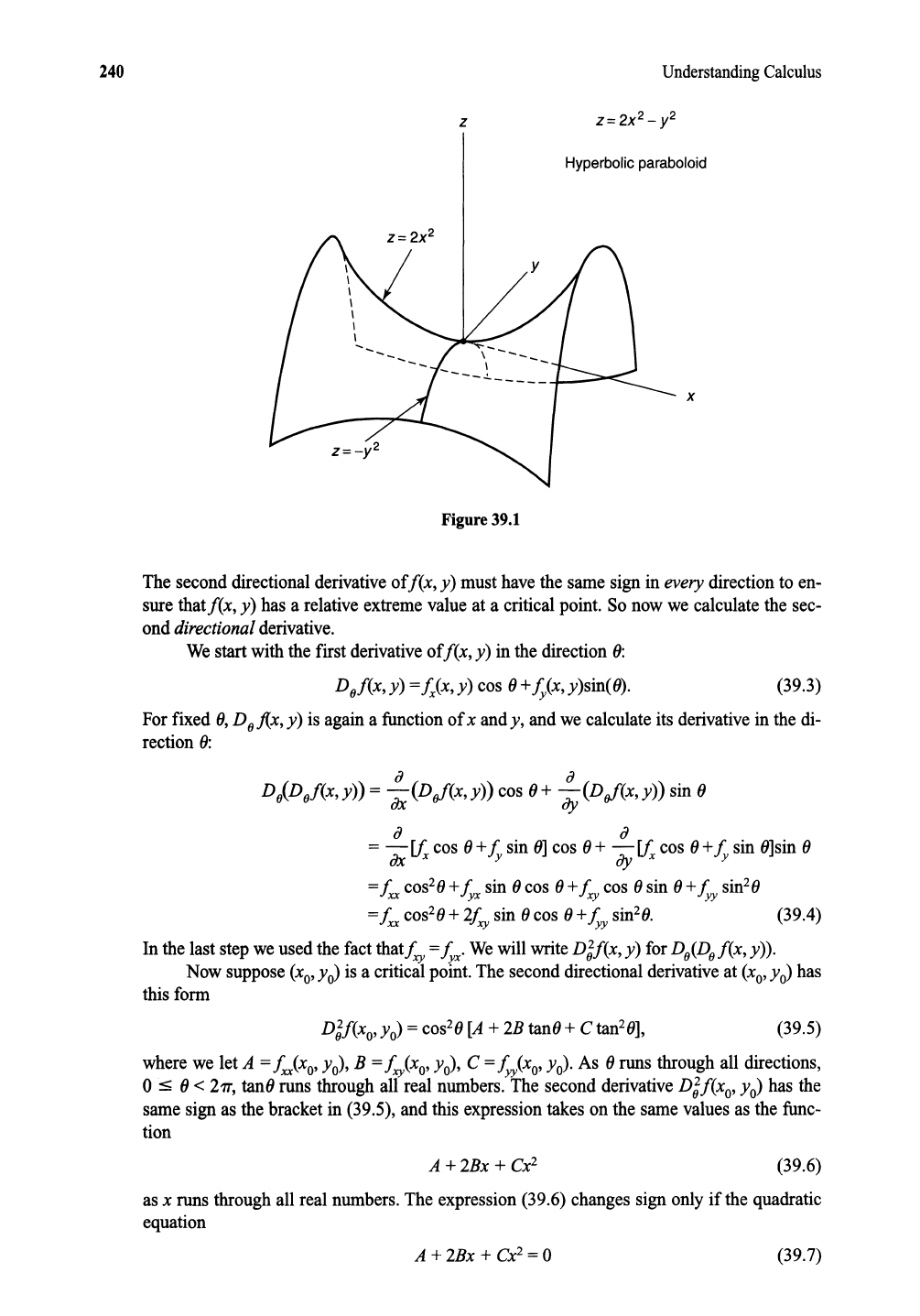
240

Understanding

Calculus

Hyperbolic paraboloid

Z=_y2

Figure 39.1

The second directional derivative

off

(x,y) must have the same sign in every direction to en-

sure thatf(x, y) has a relativeextremevalue at a critical point. So now we calculate the sec-

ond

directional derivative.

Westart with the first derivative

off

(x,y) in the direction 0:

D()f(x,y) =

h(x,

y) cos 0 +1;(x,y)sin(0). (39.3)

For fixed 0, D()j{x,y) is again a function

ofx

andy, and we calculate its derivative in the di-

rection

a a

DiDo!(x,y»

(Do/(x,y» cos 0+

(Do/(x,y» sin 0

a a

cos 0+

sin 0] cos 0+

cos 0+

sin

O]sin

=I. cos

(J+f sin 0 cos 0+i cos 0sin 0+f sin

cos

(J+

2f~

sin (Jcos (J+

J;y

sin

20.

(39.4)

In the last step we used the fact

thatf~

1;x.

Wewill write D'if(x, y) for

D()(D()f(x,

y».

Now suppose(x

Yo)

is a criticalpoint.The second directionalderivative at (x

Yo)

has

this form

D'if(x

Yo)

= cos

+ 2B

tanO

+ C tan

20],

(39.5)

where we let

A =fn(x

Yo),

B =

fxy(x

Yo),

C =!;y(x

Yo).

As 0 runs through all directions,

0 <

21T,

tanO

runs through all real numbers. The second derivative

D;f(x

Yo)

has the

same sign as the bracket in (39.5),and this expressiontakes on the same values as the func-

tion

A +2Bx + Cx

(39.6)

x runs through all real numbers. The expression (39.6) changes sign only if the quadratic

equation

A + 2Bx + Cx

= 0

(39.7)

Chapter39 • Maximaand Minima 241

has real roots. Equation(39.7)has real roots onlyif

- AC

;::=

Therefore,

Dtf(x

Yo)

al-

ways

has the samesign if B2- AC <

This is the sufficientcondition we

need:

If!x(x

Yo)

= 0 and!y(x

Yo)

= 0, andf2 (x

Yo)

fxx(x

Yo)fyy(x

Yo)

< 0,

thenf

has a relative

maximum

at (x

Yo)

iff.J~o'

Yo)< 0,

andfhas

a relative

minimum

at (x

Yo)

iffxx(x

Yo)

The quantityD =f;y(x, y) -

fxx(x,

y}fyy(x,

y) is calledthe discriminant

offat

(x,y).

EXAMPLE

39.1

Findall relative maximaand minima

off

(x,y) = x

- 2x -

4y2.

Solution

Wefirst find all criticalpoints.

!x(x,y) = 2x - 2 !;(x, y)=-8y.

The onlypointwhere2x- 2 =0 and

-8y

=0 is (1, 0). Nowcheckthe secondpartials.

fxx(x,y) = 2

fyy(x,

y) = -8.

Sincefxxandfyyhaveoppositesignsat (1,0) there is no relativemax or min.

EXAMPLE

39.2

Findall relative maximaand minima

off(x,

y) = x

-I

+3xy.

Solution

Wefirst find the criticalpoints.

t(x,

y) = 3x

+3y,

!;(x, y)=

-3y

+ 3x.

Nowsolvesimultaneously the equations

+y = 0

-y

+x=

Fromthe secondequationwe havex = y and substituting this in the first equationwe get

(1)2 +Y = 0,

y(y3

+ 1)= 0,

y=Oory=-l.

Ify

= 0, then x = 0, so (0, 0) is one critical point.

Ify

-1,

then x = 1, so (1,

-1)

is the other critical

point.

Nowcalculatethe discriminant at each criticalpoint.

fxx(x,

y) = 6x

fxy(x,

y) = 3

fyy(x,

y) =-6y.

At (0,

O),fxy

3,f

O'!;y

= 0, and D = 9. SinceD is positiveat (0, 0), there is neithermax nor min at

(0, 0).At

(1,

-1),f

= 6,fxy = 3,

fyy

= 6, and D = 9 - 36 <

SinceD is

negative

at (1,

-1)

there is a rel-

ativeextremevaluethere,and

sincefxxandfyyare positiveat (1,

-1),f(l,

-1)

is a relative

minimum.

EXAMPLE

39.3

Findthe point on the planex +2y +z = 6 whichis closestto the origin.

Solution

It is clear from the geometrythat there is exactlyone point on the plane whichis closestto the origin.

Wewrite

z = 6 - x - 2y to expressthe distanceas a function of x andy:

242

Understanding Calculus

f(x,y)

+Y +

+Y+ (6

-x-

2y)2.

Wewantto findx andy wheref(x,y) is

minimum.

This is evidently the samepoint (x,y) wheref(x, y)2

minimum,

so considerg(x) =

f(X)2

insteadoff(x) to simplifythe calculation.

g(x)

(6-x-2y)2

41-12x-24y+

4xy

= 2x

+ 51 + 36

-12x-

24y + 4xy.

At the minimumpointwe must havegx(x,y) =gy(x,y) =0, so we solve

gx(x,y) = 4x

-12

+ 4y = 0

gy(x,y) =

10y-24+4x=0.

Werewritethe twoequations as

x+y=3

2x +5y= 12.

Multiplyboth sides of the first equationby 2 and subtractto get 3y = 6, y = 2. Fromthe first equation

we then get

x = 1.Therefore (1, 2) is the onlycriticalpoint forg(x, y), and hencethe only criticalpoint

forf(x,y).

Atx

l,y

= 2,

Z = 6 - x - 2y = 6 - 1 - 4 = 1.

Hence(1, 2, 1)is the pointon the planewhichis closestto the origin.In this exampleweknowfromthe

geometrythat there is a minimumat the criticalpoint so the second

derivative

calculations are not nec-

essary.

we want to find the absolute maximum or minimum that f(x, y) takes on some

bounded region then we have to consider boundary points as well as interior points.

f(x

Yo)

is an absolute maximum and (x

Yo)

is an interior point

the region R, then

course

f(x

Yo)

is also a relative maximum, and

and

1;,

will be zero at (x

Yo)·

Yo)

is a boundary point, then the partial derivatives need not be zero. Suppose f(x, y) = x

and we want the maximum value

f(x, y) on the rectangle R

points (x, y) with 1 -s x

-s 3, 0

=::;

y -s 1. The answer is obvious since f(x, y) is the square

the distance from (x,

y) to the origin, and the point

R farthest from the origin is (3, 1). However,

= 2x and

= 2y, so neither derivative is zero at (3, 1).

there are no critical points in the interior

the region, then the maximum and minimum will occur on the boundary, and one looks

only at boundary points.

EXAMPLE

39.4

Findthe maximumvalue

off(x,

y) = xy + 3x -

yon

the trianglewith verticesat (0, 0), (2, 0), and (0, 4).

(Figure39.2.)

Solution

Wefirst checkto see if thereare criticalpointsin the interior.

~(x,y)=y+3

.!;,(x,

y) =

x-I.

The only critical point is (1,

-3)

which is not in the

region.

On the segment0 -s x

2,f(x,

y) = 3x,

so 3

·2

= 6 is the maximumvalue on this side. On 0

4,f(x,

y) =

-y,

so 0 is the maximumon

this side. On the segmentfrom (2, 0) to (0, 4),

y =

-2x

+ 4, so

f(x, y) = x(-2x +4) + 3x - (-2x + 4)

Chapter39 •

Maxima

and Minima

Figure 39.2

243

-2x

+4x +3x+2x- 4

=-2x

+ 9x - 4.

Nowwewantthe

maximum

valueof the quadratic

function

q(x) =

-2x

+ 9x - 4 for 0 -s x

2. Wecal-

culate

q'(x):

q'(x)=-4x+9.

Onthe interval 0 -s x -s 2, q'(x) > 0 so q(x) is increasing, andq(2) = 6 is the

maximum

value.

Themax-

imum

off

(x, y) occursat (2, 0), and the

maximum

valueis 6.

PROBLEMS

Findall relative maximaand

minima.

39.1

f(x,y)

+ y.

39.2

f(x,

y) = x

+ 4xy +

2Y.

39.3

f(x,y)

- 3xy

+y.

39.4

f(x,

y) = x

+Y - 2x.

39.5

f(x,

y) = x

Y + 2x- 4y + 1.

39.6

f(x,

y) = 3x

+ x

6x - 3y.

39.7

f(x,y)

= y3

-x

+2x +

3Y.

39.8

f(x,y)

siny

39.9

f(x,y)

siny

39.10 Findthe point on the plane2x +y +z = 6 whichis closestto the

origin.

39.11 Findthe point on the planex +y +z = 1whichis closestto (2, 3, 6).

39.12 Find the

minimum

valuethat the functionf(x, y) = xy + 3x - y of

Example

4 takeson the

closedtriangle withvertices (0, 0), (2, 0), (0, 4).

39.13 Find three positive

numbers

x, y, z suchthatx + y + z = 20 and xyz is

maximum.

Hint:

Maximize

the functionf(x, y) = xy(20 - x - y) forx andy positive andx + y

20.

Double Integrals

Let z = f(x, y) be a function of two variables defined on someregionR in the

xy-plane.

The

doubleintegral off(x,Y) overR is a limitof

Riemann

sums:

ff(x,y)dA=

lim

If(xi,y)aA

i·

aAr-+o

i=1

(40.1)

Toform the sum on the right side of (40.1)we

divide

the regionR up into smallsubregions

Rl'R

•••

, R

and let

be the area of R

and

(Xi'

)

be a point in

Iff(x,

y) is a pos-

itive

function,

then

f(x

y)aA

is the

volume

of a small solid whosebase has area aA

and

whose

height

isf(xi,

y).

(Figure

40.1.) Thusj'(x;

y)aA

is approximately the

volume

over

R, and under the surfacez =

f(x,

y). The

Riemann

sum

I;=lf(x

y)aA

is an approximation

to the total

volume

over R and under the surface. The Riemann sums approach a limit as

the subregions are taken smallerand

smaller,

with all

approaching zero, and this limit

is the

double

integral f

ff(x, y)dA. The

volume

overR and under the surface is defined to

be the integral.

have already calculated the

volumes

of some solids which were solids of

revolu-

tion. Recallthat to find the

volume

obtainedby rotatingthe area undery = f(x) aboutthe x-

axis, for a -s x -s b,we slice the solid into discs ofradiusf(x) and thickness dx. The

volume

of sucha disc is

7T'

f(X)2dx

and the total

volume

(Figure

40.2)

V= t7Tf(x)2dx.

Not all

volumes

are

volumes

of revolution, but our general approach to finding vol-

umesusesthis samesort of slicingtechnique. Let

z =

f(x,

y) be a surfaceoverthe rectangular

region

R consisting of points (x, y) with a -s x -s

band

c ::; y -s d.

(Figure

40.3.)

fix a

245