Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

224

Understanding Calculus

Fora

function

z =f(x, y) of two

variables,

the differential is defined by

dz =df(x, y) =

h(x,

y)dx +!;(x, y)dy.

(36.4)

This is

simply

an alternative

notation

for the

tangent

plane

approximation

expressed

(36.3).

If dx and dy are

small,

then dz is

approximately

the corresponding

change

in z. The

notation of

(36.4)

frequently

used

instead

of the

ax,

notation of

(36.3)

because

(36.4)

suggests

the formof the chainruleswestudyin the next

chapter.

EXAMPLE

36.4

Use the differential approximation to estimatethe changesin z =

sin(xy)

as x changesfrom 0 to -0.01

andy changesfrom2.00 to 2.05.

Solution

Whenx = 0 andy = 2, z = sin 0 =

Wecalculatedz withdx = -0.01 and dy = 0.05.The partialsat (0, 2)

are:

Hence

= y

cos(xy)

= x

cos(xy)

-(0

2)=2·

ax'

(0,2) =

dz = 2dx+

Ody

= 2(-0.01) = -0.02.

The exactchangeis approximately -.0205.

In the real

world

thereareno exact

measurements.

Thenext

example

indicates howthe

differential

approximation

can be usedto see howthe

inevitable

errorsin

measurement

will

affect

a calculated

value.

EXAMPLE

36.5

Cylindrical bearings 1 em. in diameterand 2 em. long must be machinedso their weightis within 1%

of the specifiedvalue.The manufacturing processallowsa relative error in the diameterwhichis twice

the relative error in the

length.

Findthe maximumrelativeerror in the dimensions whichwill keep the

weighterror less than 1

Solution

The weightof a bearingis

"4k1TJi2t,

wherek is the

density,

D the diameter, and t the

length.

The approximate error in W is

dW=

dD+

1 1

= 2k1TDtdD + "4

Ji2

The relative error in W is

Chapter36 •

Tangent

Plane and Differential Approximation

=2-+-

225

If the relative error dD/D in the diameter measurement is twice the relative error d

t in the length

measurement, then

W=5,'

If dW/Wis to be less than .01 (i.e., 1%)then

dt/tmust

be less than .002.The error in the lengthmeas-

urementmust be less than .2%,with the error in the diameterless than .4%.The error in the diameter

measurement accountsfor an error of .8% in the weightcalculation.

For

functions

u = F(x, y, z) of three

variables

the differential again

gives

a usefulap-

proximation to the

change

in the

function

for small

changes

in the

variables.

The differential

F(x,y, z) is

dF(x,

y, z) =

Fx(x,

y, z)dx+

Fy(x,

y, z)dy +

Fz(x,

y, z)dz

or,in the curly-dnotation,

au au

du =

-dx

-dy

-dz.

EXAMPLE

36.6

Let u =

xI/z4·

Findthe approximate maximumpercentageerror in the calculatedvalueof u if the meas-

ured valuesof

x, y, z are off by at most 1%.

Solution

Wecalculatethe differential:

The relativechangein

u is

du 1 2 4

- = - dx + - dy - - dz.

u x y z

If dx/x, dy/y, and dzlz are all.Ol in magnitude, and dz/z is negative so the errors add up, thendu/u= .07.

Hence 1% errors in x, y, and z can result in a 7% error in the calculatedvalue of u.

PROBLEMS

Findthe twotangentvectorst

and t

and the normalvector N at the givenpoint.Writethe equa-

tion of the tangentplane at the givenpoint.

36.1 z = x

+3xy (3, 1)

36.2 z = 2x +

(1,2)

36.3 z =

e(x

+I) (0, 1)

36.4 z = y

10g(1

+ x

)

(0,2)

36.5 z = e cos y (0, 0)

36.6 z

tany

+ x

+ y (3,0)

Find the points on the givensurfaceswhere the tangentplane is horizontal.

36.7

z=xy+x

36.8 z = x

+1 - 2x

226

Understanding Calculus

36.9 z = x

3x +I

36.10

z=x

+xy +I +2x +2y

Use the differential approximation to find approximate values forz at the givenpoint.

36.11 z =

xy2

(2.9, 3.1)

36.12 z = xty' (1.3,-2.1)

36.13 z =x

+y (.9,3.2)

36.14 z = x cosy (3.1,-0.1)

36.15 z v xer (1.1,0.1)

36.16 What percent error is allowable in length and diameter of the bearings of Example 5 if

the percenterror is the same for length and diameterand the maximumallowable error

for weightis 1

(37.1)

Chain

Rules

Recall the chain rule for differentiating functions of one

variable:

if y is a

function

of x,

=f{x), andx is a function of t, x =g(t), theny is a function of t, and

: =

~j(g(t)

(g(t)g'

(t) = : : .

The equation

dy=dydx

dt dx dt

most clearly reflects what happens in chain rule differentiation.

t changes by an amount

at,

thenthis causesa change

in x, whichin turn causesa change

in y. The

derivative

the limit of

also approaches zero, so

ay ay ax

dy dx

-=-.-~_.-.

(37.2)

dx dt

Nowwe considerchainrules for functions of two or more variables, eachof whichis a

function of one or more

variables.

As a first case,suppose z is a function ofx andy, andx and

yare

functions of t. Thenz becomes a

function

of the single

variable

t, andwewanta

formu-

la for

Let

be an arbitrarychangein t, and let

and

be the corresponding changes

in x and

y. Thechange

in z whichcorresponds to

changes

and

in x andy is

approx-

imately

Therefore

= h(x,

y)ax

!y(x,

y)ay. (37.3)

(37.4)

227

228

Understanding Calculus

andthe errorin

(37.4)

goesto zerofasterthan

I~I

l~yl.

Hence

dz .

dx dy

=l:~o

h(x,Y)dt

+!;(x,y) dt · (37.5)

In the curly-dnotation this reads

-=--+--

EXAMPLE

37.1

Find

at t =2

ifz

<xer+

xy2,

withx =

(l,y

=2t +3.

Solution

Using(37.6)we write

dz a

dad

- =

-(xe

xy2)-(P)

-(xe

xy2)-(2t

+ 3)

= (e

y)(2t)

+ (xe

2xy)(2).

Whent =2, x =4 andy = 7, so at t =2,

= (e

+ 49)(4)+ (4e

+ 56)(2)

12e

+ (4 . 49 + 2 . 56)

12e

308.

(37.6)

Now

suppose

z = f(x, y) and x and

yare

both

functions

of two new variables

rand

Thenz

becomes

function

rand

s, and we wantto calculate : and

start with the

samedifferential approximation for

!:.~+

~y.

The

changes

and dy now

depend

and ds as

follows:

ax ax

-dr+-ds

as'

~r+

ds.

Tofind : weholds

fixed,

= 0, and

(37.7)

ax=

-~r

Nowweuse these

formulas

(37.7),

with

= 0, to get

~=--~r+--~r.

Theerrorin

(37.8)

goesto zerolike e(dr) · dr,

where

e(dr)

0, so

. !lz

-=hm-=--+--.

~r~O

The

companion

formula

for

(37.8)

(37.9)

Chapter 37 • Chain Rules

-=--+--.

229

(37.10)

EXAMPLE

37.2

Letz

withx andy functions

ofr

ands suchthat

ifr=

1ands =2, thenx =

3,y

=4, : = 5, and

= 6. Find

when r = 1, s = 2.

Solution

Weuse (37.10):

-=--+--

as'

a By

-(x

1)-

-(x2

1)-

=2x-

+3r-.

At r = 1,s = 2, we have

- = 2(3)(5) +

3(4)2(6)

=30 + 288 =318.

Ifwe are

given

explicit

formulas

forx andy in terms

ofr

ands, thenwecanwritez ex-

plicitly in termsof r ands and

calculate

t:,

directly.

Thisis not a possibility in

Example

because

therewe

were

given

information aboutthe

variables

andtheir

derivatives

onlyat the

single

pointcorresponding to r = 1,s = 2. In thenext

example

express

z in termsof

rand

s anddifferentiate

directly.

EXAMPLE

37.3

Letz =

reX,

with x = rs andy =y2+ S3. Find

at r = 1,s =

Solution

Substituters for x and y2+ S3 for y:

Now calculate : directly:

Atr=

l,s=O,

- = [4(1 + 0) + 0]e

= 4.

Notice that this is NOT a chain rule calculation.

EXAMPLE

37.4

Supposez is a function of u and v, and u and v are functionsx andy. At

(xo'Yo)'

X= 3,

= 4,

= 5,

av - 6 Wh .

( )?

an dy

at IS dy at X

230

Understanding Calculus

Solution

Herethereis no question of writingz as an explicitfunction

ofx

andy,

but we are givenenoughinfor-

mationto

answer

the

question.

Firstthe

general

formula,

(37.10), withx

andy

replacedby u and v, and

r ands replaced by x andy

az az

-=--+--

aye

Nowsubstitute the givenvaluesat (x

Yo):

=3 . 5 + 4 . 6 = 15+ 24 = 39.

Forfunctions of three or morevariables the chainrule patternsare similar. Here are two

examples:

u =

f(x,

y, z); x, y, andz are functions of t.

du=audx+audy+audz

_ dx dy dz

f,(x,y,

z)-

f(x,y,

z)-

f,(x,y,

z)-.

x dt Y dt Z dt

B. u =

f(x,

y, z), and x, y, Z are functions of

rand

au au

-=--+--+--

iJr

-f,(x,y,z)-

+f(x,y,z)-

+f,(x,y,z)-.

Y iJr Z

Now considera 3-part chainrule situation. Let u be a functionof x andy, withx and y

functions of

rand

s, and r and s functions of t. The basic differential formulas provide the

properpattern.

du = u dx + uydy,

=xrdr + xds,

dy =

ydr

+ysds,

dr=

r'dt,

ds=s'dt.

Now put these all together:

du=udx+udy

x y

= u (x

dr+x

ds) +u (y

dr+

u ds)

x r s y r s

Hence

- = u (x r' + x

s')

+ u (y r' +y s').

dt x r s y r s

Chapter

37 • ChainRules

231

EXAMPLE

37.5

Let u = x +y, x =

r-,

y = r + 1, r = fl. (So u is a

function

of two

variables

andy,

eachof

which

is a

function

of one

variable

r, andr is in turna

function

of t.)

wantto find

~~.

Solution

du = uxdx+ uydy

dx dy

-dr+u

-dr

x dr y dr

dx dr dy dr

dt+u

dt.

x dr dt y dr dt

Hence

du dx dr dy dr

-=U--+U--.

dt x dr dt y dr dt

EXAMPLE

37.6

Calculate

cosx

2dx.

Solution

The

integral

f cosx

2dx

is not onewecanwriteout

explicitly.

However,

if weletF(u) = f

(;

cosx

2dx,

know

thatF' (u) =cos u

Sothe

problem

is to find

-9tF(

where

u =t 2. The

answer

simple:

d du

dt F(u)

F'(u)dt

= (cosu

)2t = (cos f)2t.

PROBLEMS

Writeoutthe

appropriate

chainruleandthenuse it to findthe

indicated

derivative.

37.1 z

2xy;

X= r +s, y =

r-s.

Find

atr=

l,s=2.

37.2 z = xe

;

x = r + s, y = 3s

+ s.

Find

at r =2, s =0.

37.3

z=x

;

x=rs,

y=3r-s.

Find : at r = 1,s

=-1.

37.4

z=ucosv;

u=2x+y,

v=xy2.

Find

atx = 0, y = 2.

37.5 U=X

2+y2+

Z2;

x=t,

y=t

z=t

•

ddu

FIn dt at t = 2.

37.6 u = 2x +

3,yZ

4z3,

and x, y, z are functions

t. Find

at a point towhere x = 1, y = 2,

z=3,

:=5,

~=6,

:=7.

37.7

u=X

2y+

x=t+s,

y=t

2-s

z=2t.

Find

when

1,s = 2,

ind

7. FIn dt at (2, 3,4) I V = xyz andat (2, 3,4), dt = -1, dt = 0, dt = 3.

37.9 A point moves on the surface z = Xl + 3xy so that

;;

= 3 and

= 4. Find : when the

point

passes

through

(5,2, 55).

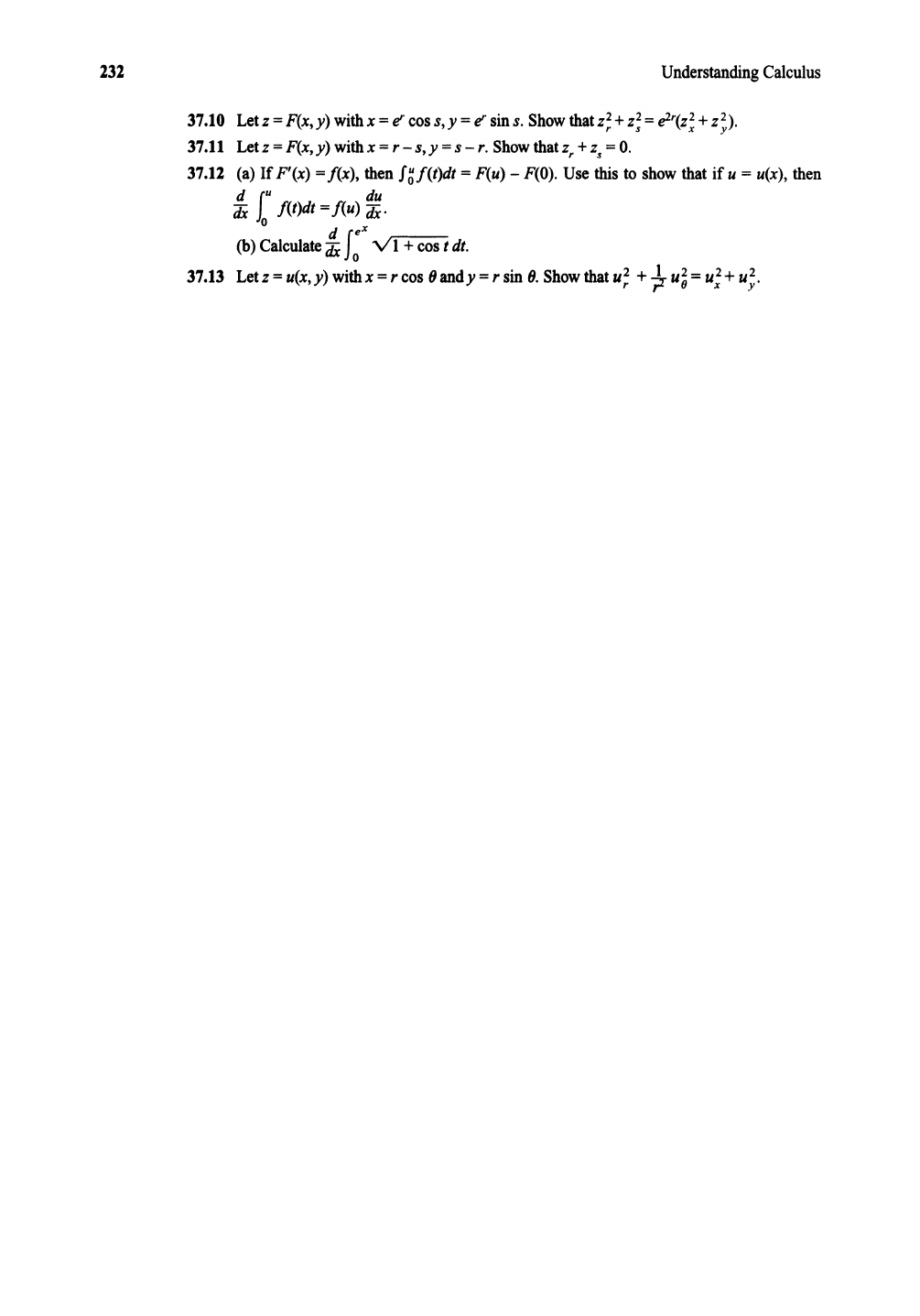
232

Understanding

Calculus

37.10 Letz =F(x,y) withx =e"coss, y =e sins.

Show

thatz; +z; =

e2r(z~

+z;).

37.11

Letz =F(x,y) withx =r

-s,y

=s - r.

Show

that

+Zs =

37.12 (a) If F'(x) =f(x), then

f~f(t)dt

=F(u) -

F(O).

Use this to showthat if u = u(x), then

dx 0 f(t)dt = f(u) dx:

fex

(b)

Calculate

dx 0

+ cos t dt.

37.13 Letz =u(x,y) withx =r cos 9 andy =r sin 9.

Show

thatu; + *

= u; +

u;.

Gradient and

Directional Derivatives

have

seenthat the partial

derivative

h(x

Yo)

gives

the slopeof the curve

where

theplane

x = X

intersects the surface z = f(x, y). Nowwe will find the slopeof the curve

where

an ar-

bitraryvertical plane intersects the surface

z =fix, y).

(Figure

38.1.) Fix a point (x

Yo)'

and

consider an arbitrary line in the

xy-plane

through (x

Yo).

If the line

makes

an angle 6 with

thex-axis, thenthe linehas the parametric equation

x = X

+s cos 6

y =

+s sin 6. (38.1)

In therepresentation (38.1),s is the

distance

from(x,y) to (x

Yo)'

since

Y(x

-X

)2+ (v -

YO)2

= Y

s2cos26

+ s2

6 = s.

Since

gives

the distance alongthe line,the slopeof the line

is~.

By the chainrule

-=--+--

az az

= - cos 6+ - sin 6. (38.2)

The right side of (38.2) is the directional derivative of z (or

!(x,y»

in the direction

9.We'll use the notation DOZ or Do!(x, y) so

=Do!(x, y) =!x(x,y) cos 6+!;(x, y) sin

(38.3)

If 6 = 0, then the line is parallelto the

x-axis,

sin 6 = 0, cos 6 = 1, and Do!(x, y) =!x(x, y).

Similarly,

if 8 =T' then

f(x,

y) =!y(x, y).

233