Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

182 Understanding Calculus

if k

r, and has the form

k = r.

Tofind a particular solution

(30.1) if

q(t)

= e

Qn(t), try Y = e

Sn(t) if e

is not

a solution

the reduced equation,

and

try y = e

t S; (t) if e" is a solution

the reduced

equation.

Here are some examples

this rule. In all these examples, the reduced equation is

f,f

- 3

+ 2y =0, with solutions e' and

e",

(a)

6e-

There is a particular solution

the form y =

Ae-

•

(b)

+ 2y = e .

Since

is a solution

the reduced equation, there will be a solution

the form

e'.

+2y = 4t

•

There is a solution

the form y =

(At

C)e

•

(d)

+2y =

(-6t

+8)e .

There will be a solution

the form y =

(At

Bt)e

since e

is a solution

the

reduced equation.

(e) dt

+ 2y = 4t.

This is the problem

Example 30.1. Now we know there is a solution

the form

+ B, so we can substitute this general linear polynomial and determine A and B.

That's a whole lot simpler than the calculations

Example 30.1.

The same kind

argument we used above shows that if q (t) = Qn(t) cos a t or q (t) =

Qn(t) sin

for a polynomial Qn(t), then there will be a solution of the form

= Rn(t) cos or + Sn(t) sin

at.

Notice that both cos

and sin

must occur in the trial solution, even if

q(t)

involves one

these functions. For example,

q(t)

= 3

sin4t,

try y = A

cos4t

+ B

sin4t;

if q (t) =2t cos t ,

try Y =

(At

+B)

cost

(Ct

+D)

sint.

If cos

and sin

are solutions

the reduced equation, both R; (t) and S;(r) must be

multiplied by

EXAMPLE

30.2

Solve - - - - 2y = IOcost.

dt? dt

Chapter 30 • Nonhomogeneous Second-Order Equations

Solution

The auxiliary equation is

183

m - 2 = (m - 2)(m + I) =0,

so e

and

e:'

are solutions of the reduced equation. There will be a particular solution of the form

y = A cos t + B sin t, so we calculate derivatives and substitute:

y = A cos t + B sin t

dy = B cos t - A sin t

= - A cos t - B sin t.

dt?

Substituting in the equation gives

(cost)(-A

- B -

2A)

(sint)(-B

+ A -

2B)

10cost,

(- 3A - B) cos t + (A - 3B) sin t = lOcos t.

Hence, we must have

-3A

- B = 10

A - 3B =

Multiply the first equation by - 3 and add:

lOA

-30,

A =

-3.

This gives B =

-3A

- 10 =

-1,

and hence

y = - 3 cos t - sin t.

EXAMPLE

30.3

Solve dt

+ 4y =4 sin 2t.

Solution

Here cos 2t and sin 2t are solutions of the reduced equation, so the trial solution has the form

y =

cos 2t + B t sin 2t,

dy = A cos 2t -

2At

sin 2t + B sin 2t +

2Bt

cos 2t

= (cos

2t)(A

2Bt)

+ (sin

2t)(

-2At

+ B)

-2

= (cos

2t)(2B)

2(A

2Bt)

sin 2t

+(sin

2t)(

-2A)

+ 2(

-2At

+ B) cos 2t

= (cos

2t)(

-4At

4B)

+ sin

2t(

-4Bt

4A).

Substitution in the equation gives

(cos

2t)[4B] + (sin 2t)[

-4A]

= 4 sin 2t.

Hence,

and the solution is

-4A

=4,

=0,

A=-l

y =

-t

cos2t.

184

Understanding Calculus

PROBLEMS

JO.1

(a) Integrate by partsto showthat if n

2::

ftne

dt =

~tneCl

ftn-le

(b) Use (a) and fecI dt =

~ecI

to integrate the

following

in tum:

fte" dt, ft

dt, ft

dt.

nth degreepolynomial and c

=1=

Finda particular solution usingthe

examples

(a)-(e) in the text.

y dy

-I

JO.2

3dt + 2y = 6e

(Example

(a»

30.3 dt

3dt + 2y = e

(Example

(b)

30.4 - -

+ 2y = 4t

(Example

(c)

dt? dt

dy u

30.5 dt

3 dt + 2y =

(-6t

+ 8)e (Example (d)

30.6

3dt + 2y =4t

(Example

(e»

30.7 Solve

- *-2y = IOsint.

30.8 Solve

+Y =

6cost.

30.9 Solve

+ y =

-25sin2t.

JO.10

Solve

+ 2y = e'

cost.

Hint: Try y =

Ate

cost

Bte'

sint.

Vectors

Some

physical quantities are determined by a single

number.

For

example,

temperature

is so

many

degrees,

distance

is so manyfeet, time is so many

seconds.

Otherquantities, such as

force

and

velocity,

have

both a

magnitude

anda

direction.

A quantity whichhas both

magni-

tudeanddirection is calleda vector. Whenwe dealwith

vectors

ordinary

numbers

are

some-

timescalledscalars to makethe distinction.

use bold facelettersA, B, F, v, etc. for vec-

tors,and ordinary letters

a, b,k,v,x, y for

scalars.

Vectors

are represented geometrically by a directed line

segment;

i.e.,

a line

segment

with an arrowhead on one end.The lengthof the

segment

is the

magnitude

of the

vector-

for

example

the

number

of feet per secondfor a velocity

vector.

The direction of a vectoris

the direction of the line segment-for a velocity vectorthat is the direction

where

the object

if headedat so manyfeetper

second.

will start with plane

vectors

to keep the notation

simple.

The vector from

P =

(xl'

to Q =

Y2)

denoted

PQ, and its

magnitude

or norm is

given

IIPQII

=V(x

X\)2

+ (Y2 - y\)2.

Vectors

are not tied to a particular point in the plane, so two

segments

with the same

lengthand same direction represent the same

vector.

(Figure

31.1). For

example

the vector

from

(0, 0) to (2, 1) is the sameas the vectorfrom(2, 2) to (4, 3) andthe vectorfrom(-2, 1)

to (0, 2).

Vectors

are addedin the waythatreflects howvectorquantities suchas

force

veloc-

ity add up in a

physical

situation. Toadd two

vectors

A and B put the tail of B at theheadof

A. Thevectorfromthe tail of A to the head of B is the sumA + B.

(Figure

31.2).

Thevector

forms

diagonal

of the parallelogram

whose

adjacent sides are A and B.

Figure

31.2

shows

thatB +A is the sameas A +B, so vectoraddition is a

commutative

operation:

A+B=B+A.

Figure

31.3

shows

thatvectoraddition is also

associative;

i.e., that

(A + B) + C = A + (B + C).

18S

186 Understanding Calculus

(4,3)

(2,2)

(0,2)

(2,1) (3,1) (4, 1)

•

••

-2

-1 2

-1 (1, -1)

Figure

31.1

Figure

31.2

Figure

31.3

Hence we can write A + B + C without parentheses, and vector sums can be written in any

order. For example,

A + B + C = B + C + A = C + B + A.

To make the connection between vectors and the coordinate system we introduce

unit

vectors i

andj

parallel to the axes: i is the vector from (0, 0) to (1, 0),

andj

is the vector from

(0, 0) to (0, 1). (Figure 31.4). Clearly

andj

have length one, so

lIill

IIjll

= 1.

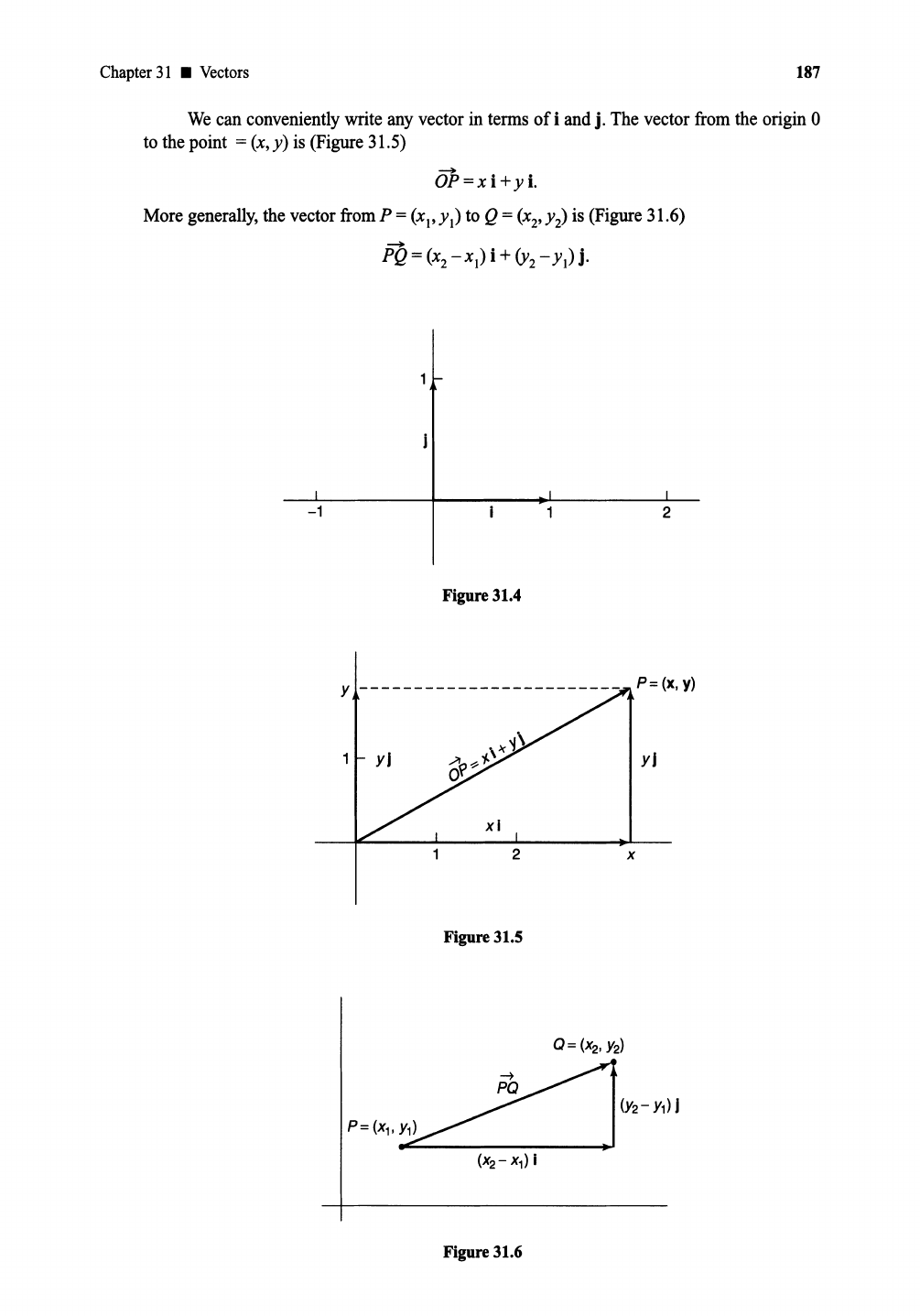
Chapter31 •

Vectors

187

Wecan conveniently write any vector in terms of i and j. The vector from the origin 0

to the point = (x,y) is (Figure31.5)

--+

OP=x

i +

yi.

More generally, the vector fromP = (Xl'y 1)to Q=

Y2)

is (Figure31.6)

--+

PQ =

-Xl)

i +

(Y2

- Y

)

-1

Figure 31.4

(x, y)

2 x

Figure 31.5

Figure 31.6

188

Understanding Calculus

-B

A+(-B)

Figure

31.7

A-B

IfB

hasthe same

magnitude

as A but the

opposite

direction wewriteB = -A.

Hence

=xi +yj, thenB =

-A

=-xi - yj.

Clearly

A + (-A) is the zero vector 0 =

OJ.

Thezero

vector

is the onevectorwithno

direction.

naturally defineA - B to be A + (-B).

(Figure

31.7).

Geometrically,

A- B is the

vector

from

thetip of B to the tip of A whenA andB orig-

inateat the same

point,

so A - B is the vectoryouaddto B to getA. If A =ali +a

j andB =

bli

j, then

A + B = (a

+ b

)

i + (a

+ b

)

A - B = (a

)

i +(a

)

Multiplying

vector

A by a

positive

scalark

gives

a vectorin the samedirection and k

timesas

long.

For

example,

2A has the samedirection as A and twicethe

magnitude.

If the

scalar is

negative,

the direction of the vectoris

reversed.

have

already seen that

-A

(-I)A has the

opposite

direction to A andthe same

length.

general,

kA is

1"1

timesas long

as A andpointsin the sameor

opposite

direction

depending

whether

k is

positive

nega-

tive.

(Figure

31.8).

It is easyto checkthat

k(A

+ B) =

+ kB.

In termsof i andj this says

+ y j) =

lex

i + ky j.

Figure

31.8

Chapter31 •

Vectors

EXAMPLE 31.1

LetP = (2, 1) and Q = (5,

-3).

Solution

(i) Write

in terms

ofi

and j.

(ii) Find

UPQII.

(i)

=(5 - 2) i + (-3 - 1) j =3 i - 4 j.

(ii)

IIPQII

= vJ2+42 = V25= 5.

189

EXAMPLE 31.2

Let P = (1, 2) and Q= (5, 3). FindthepointR on the segmentfromP to Qwhichis

of the wayfromP

toQ.

Solution

Let P be the vectorfromthe originto P = (1, 2) and Q be the vectorfromthe originto Q= (5, 3). Then

Figure31.9)

P = i + 2j,

Q= 5i +3j,

=Q - P =4i + j.

If R is the vectorfromthe originto pointR, then

R=P+

3PQ

(i + 2j) +

3(4i

+ j)

=(1+~)i+(2+i)j

= 3

+ 3

SinceR =

is the vectorfromthe originto R, R is the point

(~, ~).

Q=(5,3)

Figure 31.9

190

Understanding Calculus

Nowlookbackat whathappenedin the precedingexample. Tofind the point

(x,y)

whichis one-

third of the wayfrom

P =

(xl'

to Q= (x

' Y2)you add

~(X2

- Xl) to Xl to get X, and add

~(y2

- Yl) toYl

to gety. Forexample,the pointi of the way from (-1, 2) to (3, 5) is (x,y), where

7 28

x=-1

8(3-(-1»)=-1

7 21

y=2+

8(5-2)=2+

S·

EXAMPLE

31.3

Find the point R = (x, y) on the line through P = (0, 1) and Q= (5, 2) so that P and R are on opposite

sides of

and R is twice as far from Qas Pis.

Solution

Ifwe let P, Q, and R be the vectorsfrom (0, 0) to P,

and R respectively, then

R=Q+2P"Q

=Q+2(Q-P)

3Q-2P.

SinceQ = 5i + 2j and P = j,

= 3(5 i +2 j) - 2 j

=15i+4j.

HenceR = (15,4).

EXAMPLE

31.4

A boat heads directlyeast acrossa riverwhichruns north-south and is

flowing

due south at 5 mph.The

boat movesat 10 mph through still

water.

What is the velocityvector and speed of the boat, and how

long does it take to crossthe milewide river?

Solution

The boat's velocityvector throughthe water is 10i (10 mph due east), and the river's velocityvector is

-5j

(5 mph due south).Hencethe resultantover-the-ground velocityof the boat is v = 10i- 5j, and the

boat's speed is

IIvll

Vill

11.~h.

FromFigure 31.10we see that if s is the length

of the boat's path, then

i =

""W.

The speed is V125mph, so the time for the crossingis

Vill

1 1

t = M=

-10-

Vill

= 10hr.

The time is the same as if the boat were going one mile through still

water.

Of course if the captain's

ambitionwas to landdirectlyacrossthe riverfrom the startingplace then he is off by half a mile.

10 I

----------~----------------

-5J

.....

............5 ...

..........

1 mi

...............

Figure 31.10

Chapter31 •

Vectors

191

EXAMPLE

31.5

LetP,

R be the verticesof a

triangle.

Let P, Q, R be the

vectors

fromP,

R to the midpoints of the

opposite

sides.

Showthat P +Q+R = O.

(Figure

31.11).

Solution

Firstnoticethat

jiQ

= O. NowwriteP, Q, and R in termsof

jiQ,

QR,

and

RP:

Therefore

-+ -+

P+

Q+

PQ+QR+

RP+

-(PQ+

QR+ RP)

=0+

"20=0.

EXAMPLE

31.6

In Figure31.12a 100lb.weighthangsfromtwocordsas

shown.

Findthe tensionin eachcord.

Solution

If F

and

are the

forces

exertedby the two cords, then their respective tensions are

IIFIII

and

IIF211.

The horizontal components of F1 and F2must cancel (HI =

-8

) since the

weight

isn't

moving

side-

ways.

Therefore

The two verticalcomponents VIand V2must havemagnitudes whichadd up to 100 sincethe weight

alsois not

moving

up or

down.

Hence

Therefore, since

III

~IIF211

I~""'''''

.........

..............

..........

........

."------------~---------~

Figure 31.11