Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

14.2 Evolution: instabilities and collapse 501

0.8

0.6

0.4

0.2

t / P

(r > r

)/M

irr

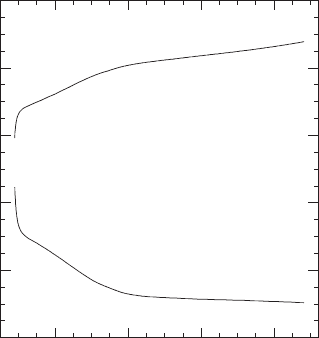
Figure 14.15 Evolution of the irreducible mass and the total rest mass outside the apparent horizon. [From

Duez et al. (2006a).]

gamma-ray burst source.

They have followed up this suggestion by performing fur-

ther simulations with a more realistic nuclear EOS, and these appear to strengthen the

argument.

It is interesting to compare the evolution and ﬁnal fate of a magnetized hypermassive star

with dynamically stable, differentially rotating, magnetized stars that are not hypermassive.

Consider two distinct categories of differentially rotating, nonhypermassive conﬁgurations:

(1) “normal stars”, which have rest masses below the maximum achievable with uniform

rotation, and angular momentum below the maximum for uniform rotation at the same

rest mass, and (2) “ultraspinning stars”, which have angular momentum exceeding the

maximum for uniform rotation at the same rest mass. Suppose they are again threaded by

a weak, initially poloidal magnetic ﬁeld with C = max(b

/P) = 2.5 × 10

−3

. Simulations

in axisymmetry

show that a normal star evolves to a uniformly rotating equilibrium

conﬁguration. By contrast, an ultraspinning star cannot settle into a uniformly rotating

equilibrium state. Instead, it evolves to an equilibrium conﬁguration consisting of a nearly

uniformly rotating central core, surrounded by a differentially rotating torus characterized

by an angular velocity that is constant along magnetic ﬁeld lines (B

∂

 → 0). Hence,

although the ﬁnal state exhibits differential rotation, it ceases to wind the magnetic ﬁeld. In

addition, the ﬁnal state appears to be stable against the MRI. It will be interesting to explore

whether the fates of these conﬁgurations are altered when the constraint of axisymmetry

is relaxed and high resolution simulations in full 3 +1 are performed.

For discussion and references to the observational literature, see Berger (2006).

Shibata et al. (2006a), Stephens et al. (2008).

Duez et al. (2006b).

502 Chapter 14 Rotating stars

600

X / M

600

500

400

300

X / M

Z / M

t = 0

0.1c

= 1800M

t − t

200

100

Figure 14.16 Snapshots of meridional rest-mass density contours (black), velocity vectors and magnetic ﬁeld

lines (green) for the initial and endpoint conﬁgurations for n = 3 magnetorotational collapse. The initial model is

identical to the conﬁguration in Figure 14.8 except that it is threaded by a poloidal magnetic ﬁeld. Field lines

coincide with contours of vector potential A

and are drawn for A

= A

ϕ,max

( j/20) with j = 1, 2,...,19 where

ϕ,max

is the maximum value of A

. In the ﬁnal, post-excision model (t

= 29 150M), the density levels are

drawn for ρ

= 100ρ

(0)10

−0.3 j

( j = 0−10). The thick (red) line near the lower left corner denotes the apparent

horizon. [After Liu et al. (2007).]

Magnetorotational collapse of n = 3 polytropes

The astrophysical and cosmological importance of massive star collapse motivates fully

relativistic simulations of the magnetorotational collapse of n = 3 polytropes. Recall that

such polytropes are useful to model very massive and supermassive stars, including “ﬁrst

generation” Population III stars, as well as the degenerate cores of massive Population I

stars. It is likely that all stars are rotating and contain magnetic ﬁelds, so it is important

to extend the calculations described in Sections 14.2.1 and 14.2.3 to include small seed

magnetic ﬁelds in the initial conﬁgurations and explore the consequences. Liu et al. (2007)

performed such simulations in axisymmetry and we will brieﬂy summarize their ﬁndings

below.

The HRSC GRMHD code of Liu et al. (2007) is closely adapted from the code of

Duez et al. (2005b) described previously. The basic setup of the simulation, including the

adjustable grid algorithm and the gauge conditions, are those used for magnetic-free n = 3

simulation summarized in Section 14.2.3. Now, however, a small poloidal magnetic ﬁeld is

inserted into the initial conﬁguration (see Figure 14.16). Once again the initial conﬁguration

is uniformly rotating near the mass-shedding limit and at the onset of radial instability to

collapse. The ratio of magnetic to rotational kinetic energy is chosen to be small (10% for

the case shown here) to study whether the ampliﬁcation of a small seed magnetic ﬁeld can

have large consequences. The simulation reveals that such magnetic ﬁelds do not affect

the initial collapse signiﬁcantly. The core collapses to a black hole, after which black

14.2 Evolution: instabilities and collapse 503

hole excision is employed to continue the evolution long enough for the hole to reach a

quasistationary state. As in the magnetic-free case, the black hole mass is M

= 0.95M

and its spin parameter is J

= 0.7, with the remaining matter forming a disk or torus

around the black hole. Once quasistationarity is reached, the spacetime metric is again

frozen (“Cowling approximation”) and the evolution of the torus continued. Interestingly,

the subsequent evolution of the torus does depend on the strength of the magnetic ﬁeld. In

the absence of strong magnetic ﬁelds, the torus settles down, following ejection of a small

amount of matter due to shock heating. When magnetic ﬁelds are present, the ﬁeld lines

gradually collimate along the hole’s rotation axis. MHD shocks and the magnetorotational

instability (MRI) combine to generate MHD turbulence in the the torus and stochastic

accretion onto the central black hole (see Figure 14.16 again). When the magnetic ﬁeld

in the initial conﬁguration is at least 10% of the rotational energy, a wind is generated in

the torus, and the torus undergoes radial oscillations that drive episodic accretion onto the

hole. At late times, the accretion rate has an amplitude of order

∼

−4

in geometrized

units, signiﬁcantly higher than the amplitude found in the magnetic-free case.

Both a collimated magnetic ﬁeld and a massive, accretion torus surrounding a central

black hole are essential ingredients for launching ultrarelativistic jets.

The black hole-

torus system observed in these relativistic simulations comprises a plausible central engine

for producing jets and long-duration, soft-spectrum (“long-soft”) gamma-ray bursts. The

simulation represents the starting point of a viable “collapsar” scenario for generating such

bursts.

The collapse of a very massive star could result in the simultaneous detection of a

gamma-ray burst and gravitational waves. In addition to a gravitational wave burst arising

from the initial collapse, the radial oscillations of the disk produce long-wavelength,

quasi-periodic gravitational waves. The oscillation period of about 500M corresponds

to an observed gravitational wave frequency f ∼1/[500M(1 + z)] ∼ 0.04(10



/M)/

(1 + z) Hz for a source at redshift z. For a very massive star with M

∼



, the signal

is in the LISA frequency band. To estimate its amplitude h, Liu et al. (2007) apply the

quadrupole formula to an oscillating disk of mass M

disk

∼ 0.05M to obtain

h ∼ 4 × 10

−23







48Gpc



, (14.51)

where D

= 48 Gpc is the luminosity distance of a source at redshift z = 5 in the con-

cordance CDM cosmology model, where H

= 71 km s

−1

Mpc

−1

, 

= 0.27 and





= 0.73.

If the quasiperiodic signal can be tracked for n cycles, where n is expected

to be a few, the effective wave strength will be increased by a factor of

√

n.Sucha

gravitational wave signal may be strong enough to be detectable by LISA.

De Villiers et al. (2005).

MacFadyen and Woosley (1999); MacFadyen et al. (2001).

Spergel et al. (2007).

See LISA’s projected sensitivity curve in Figure 9.6.

504 Chapter 14 Rotating stars

Magnetorotational core collapse to neutron stars

In previous sections we described stellar collapse to black holes using an n = 3 polytropic

proﬁle to construct the initial model and an adiabatic  = 4/3 EOS to follow the evolution.

Recall that this EOS is a good approximation for a very massive Population III star or a

supermassive star, where the pressure is dominated by thermal radiation. For a Population

I star, which has smaller mass, the pressure of the pre-collapse core is dominated by the

relativistic degenerate electron pressure, which is also well-approximated by an n = 3

polytrope initially and a  = 4/3 EOS during the early phases of collapse. But during

the ﬁnal phases, the EOS stiffens when the density exceeds nuclear density ρ

nuc

≈ 2 ×

gcm

−3

. Only if the mass of the collapsing core exceeds a critical value M

crit

will a

black hole horizon appear before the star reaches nuclear density. Otherwise, the stiffening

of the EOS can signiﬁcantly effect the collapse, causing the core to bounce and possibly

producing a neutron star remnant rather than a black hole.

Exercise 14.9 Estimate M

crit

by considering the collapse of a uniform density

sphere. A horizon appears when the areal radius of the sphere reaches R ∼ 2M.At

this time, the density is ρ

∼ 3M/(4π R

) ≈ 1.7 × 10



/M)

.Setρ

= ρ

nuc

ﬁnd M

crit

(Ans. ∼ 10M



)

For a supermassive star, the mass, which collapses homologously, is much larger than

crit

. For a Population III star of mass M = 300M



, the mass of the collapsing core is

180M



which is still much larger than M

crit

. Hence the  = 4/3 EOS is also a reasonable

approximation during the entire collapse phase for such stars.

For Population I stars, on

the other hand, the core mass is less than 2M



and a more realistic EOS is required during

the late stages. In addition, neutrino emission and transport are also dynamically important.

To simulate crudely the collapse of a magnetized, rotating stellar core of a Population I

star to a neutron star in general relativity, Shibata et al. (2006b) adopt a hybrid EOS that

consists of the sum of a cold component and a thermal component:

100

P(ρ

,) = P

(ρ

) + P

(ρ

,). (14.52)

The “cold” component, P

(ρ

), is chosen according to the prescription

(ρ

) =



(ρ

)



,ρ

≤ ρ

nuc

(ρ

)



,ρ

≥ ρ

nuc

(14.53)

where K

, K

, 

and 

are constants. Setting K

= K

(ρ

nuc

)



−

makes P

continuous

at ρ

= ρ

nuc

. Typical choices are 

≈ 4/3and

= 2.5 − 2.7. Setting K

= 5 × 10

Fryer et al. (2001).

Neutrino generation and transport also play a role in the collapse of massive stars, but are probably not dynamically

important for the most massive Population III progenitors or for supermassive stars because of their low temperatures

and densities.

100

This form follows from the work of Obergaulinger et al. (2006), who simulate magnetorotational core collapse in

Newtonian gravitation.

14.2 Evolution: instabilities and collapse 505

(cgs), ensures that the cold component represents relativistic degenerate electron pressure

for ρ

<ρ

nuc

. This simpliﬁed cold EOS is designed to mimic a more complicated, cold,

stiff nuclear EOS. The speciﬁc internal energy density, ε

, associated with the cold com-

ponent of the pressure P

is obtained by integrating the ﬁrst law of thermodynamics using

equation (14.53). The thermal part of the pressure P

plays an important role when shocks

occur, but is absent otherwise. It is given by the familiar ideal gas law

= (

− 1)ρ

, (14.54)

where ε

≡ ε − ε

is deﬁned as the thermal speciﬁc internal energy. The value of 

determines the efﬁciency of converting kinetic energy to thermal energy at shocks; the rule



= 

is adopted to conservatively account for shock heating.

Shibata et al. (2006b) use their two GRMHD codes described earlier in this section to

perform simulations of core collapse in axisymmetry with a grid of 2500 × 2500 zones.

The grid is large, and adjusted during the collapse as in the n = 3 simulations described

previously, in order to cover the full dynamic range of the imploding core and to resolve

the fastest growing MRI wavelength. Not surprisingly, they ﬁnd that signiﬁcant differential

rotation results even when the rotation of the progenitor is initially uniform. Consequently,

a seed magnetic ﬁeld is ampliﬁed both by magnetic winding and the MRI. Even if the ratio

of magnetic energy to rotational kinetic energy is quite small at the time of proto-neutron

star (PNS) formation, the ratio increases to 0.1–0.2 by magnetic winding. Following PNS

formation, MHD outﬂows lead to losses of rest mass, energy, and angular momentum

from the system. The earliest outﬂow is produced primarily by the increasing magnetic

stress caused by magnetic winding. The MRI ampliﬁes the poloidal ﬁeld and increases

the magnetic stress, causing further angular momentum transport and helping to drive the

outﬂow. After the magnetic ﬁeld saturates, a nearly stationary, collimated magnetic ﬁeld

forms near the rotation axis and a Blandford–Payne type outﬂow

101

develops along the ﬁeld

lines. These outﬂows remove angular momentum from the PNS and, as a result, the rotation

period quickly increases for a strongly magnetized PNS until the degree of differential

rotation decreases. The simulations thus suggest that rapidly rotating, magnetized PNSs

may not give rise to rapidly rotating neutron stars.

These simulations should be regarded as preliminary, prototype calculations that illus-

trate how magnetorotional collapse can be tackled in numerical relativity. A number of

simplifying assumptions have been incorporated in these simulations, including the adop-

tion of equatorial and axisymmetry, a crude hybrid EOS, and the neglect of all neutrino

transport and emission. These restrictions will have to be relaxed and the calculations

repeated with greater sophistication in the future. But the tools are in place and rapid

progress is now possible.

101

Blandford and Payne (1982).

Binary neutron star

initial data

We now turn to binary neutron star systems. In this chapter we will discuss strategies for

constructing initial data that describe two neutron stars in quasiequilibrium and quasicir-

cular orbit; in Chapter 16 we will review some simulations of their dynamical evolution,

including their coalescence and merger.

As we have already discussed in Chapter 12.1, relativistic binaries cannot possibly be

in exact equilibrium, since the emission of gravitational radiation leads to a slow inspiral.

For sufﬁciently large separations, however, the time scale for this inspiral is much longer

than the orbital period, so that we can approximate the inspiral as a sequence of binary

conﬁgurations in circular orbit. We refer to these binaries as being in “quasiequilibrium”,

and to their orbit as “quasicircular”.

In Chapter 12.3 we saw how binary black hole circular orbits are generated by a helical

Killing vector ξ

hel

(see equation 12.63 and Figure 12.4), and how this helical Killing vector

can be used to construct solutions to the constraint equations that describe gravitational

ﬁelds that are in approximate equilibrium. We will follow a very similar approach in this

chapter to construct quasiequilibrium binary neutron stars in quasicircular orbit. The added

complication here is that we also have to ﬁnd a matter distribution that is in equilibrium

with the gravitational ﬁeld.

15.1 Stationary ﬂuid solutions

To construct quasiequilibrium binary neutron stars we need to ﬁnd quasistationary solutions

to the relativistic equations of hydrodynamics. For starters, we need to ﬁnd a rest-mass

density ρ

and a ﬂuid 4-velocity u

that, given an equation of state, satisfy the conservation

of energy-momentum (5.6),

∇

= 0, (15.1)

and the conservation of rest mass (5.7),

∇

(ρ

) = 0. (15.2)

Given a one-parameter (e.g., cold nuclear) equation of state (EOS) we can express the

speciﬁc internal energy density  and the pressure P, both of which appear in the stress-

energy tensor T

deﬁned by equation (5.4), entirely in terms of ρ

506

15.1 Stationary ﬂuid solutions 507

A solution to equations (15.1) and (15.2) automatically satisﬁes the relativistic equations

of hydrodynamics, but need not be in equilibrium. Enforcing equilibrium requires an

additional condition. What we mean by stationary equilibrium is that an observer corotating

with the binary would not notice any change in the binary’s structure with time. In other

words, the binary conﬁguration at any time could be generated from its conﬁguration at any

other time by a simple coordinate transformation consisting of a rotation around the axis

of rotation. This rotation is generated by a helical Killing vector ξ

hel

(see equation 12.63)

that, like a corkscrew, is tangent to the binary’s orbit through spacetime. Such a helical

Killing vector is illustrated in Figure 12.4.

As explored in Appendix A, the Lie derivative

T of a tensor ﬁeld T along a vector

ﬁeld X

measures the difference between the actual change in the tensor ﬁeld T and the

change that would arise under a coordinate transformation generated by the vector ﬁeld X

To insure, then, that the ﬂuid quantities ρ

and u

describe an equilibrium conﬁguration,

we require these quantities to be Lie-dragged along the helical Killing vector ξ

hel

= 0 L

hel

= 0. (15.3)

It is clear that the above equations still cannot determine the solution uniquely, since

the individual stars in the binary may or may not be spinning. In the case of binary

black holes we determined the spin of the individual black holes through the horizon

boundary condition (12.107); here we will determine the spin of the individual neutron

stars by making an assumption about the ﬂuid velocity. We will see that the equations

simplify for two special, but astrophysically relevant, cases: corotational and irrotational

binaries.

The equations become especially simple for corotational binaries, whereby the spin

angular velocity of each star is equal to the orbital angular velocity of the binary (when

measured in the inertial frame of a distant observer). In such systems each star always

shows the same side to its companion. A familiar example is the Moon, which corotates

with the Earth. Since the equations simplify dramatically for corotational binaries, this case

has usually been studied ﬁrst. Unfortunately, this case is not physically realistic for neutron

stars. Maintaining synchronization (corotation) during the inspiral requires a viscosity that

acts on a time scale that is short compared to the inspiral time. It turns out that such a

large viscosity is very unphysical for binary neutron stars.

Instead, the assumption of an

irrotational ﬂuid ﬂow is more realistic for neutron star binaries, as we shall now explain.

Isolated neutron stars, like radio pulsars, are observed to have spin. However, their spin

frequencies, with notable exceptions, are small compared to the high orbital frequencies

(∼kHz) characterizing neutron star binaries at the small separations they reach prior to

merger. These orbital frequencies approach the high frequencies that isolated neutron stars

would have at break-up due to centrifugal forces (i.e., the mass-shedding limit). It is thus

reasonable to expect that typical neutron stars have much smaller frequencies when they

See Kochanek (1992a); Bildsten and Cutler (1992).

508 Chapter 15 Binary neutron star initial data

form a binary. Viscous interactions cannot spin up such a star signiﬁcantly during the

inspiral. Tidal and gravitational radiation reaction forces conserve circulation; in fact,

circulation is strictly conserved for isentropic ﬂow (this is the Kelvin–Helmholtz theorem,

proven for relativistic ﬂow in Chapter 5.2.1). We therefore expect binary neutron stars to

maintain their low spin frequencies during inspiral. Therefore, at small separations, the

ﬂuid motion in neutron star binaries can be well approximated as irrotational.

Most studies of binary neutron stars assume the opposite extremes of corotational or

irrotational ﬂuid ﬂow,

and in the following we also will focus on these two limiting cases.

We will show how the Euler equation (15.1) reduces to an algebraic equation in both cases,

and will see how the continuity equation (15.2) is satisﬁed identically for corotational

binaries and can be recast as an elliptic equation for irrotational binaries. However, before

going through this formal derivation in general relativity, it is instructive to derive the

corresponding equations in a Newtonian framework.

15.1.1 Newtonian equations of stationary equilibrium

The spatial components of equation (15.1) yield the Euler equations (5.14), which in the

Newtonian limit reduce to

∂

+ v

=−

P − D



. (15.4)

Here 

is the Newtonian gravitational potential and is a solution to Poisson’s equation,



= 4πρ

. (15.5)

In the Newtonian limit, the continuity equation (15.2) becomes

∂

+ D

(ρ

) = 0. (15.6)

The ﬁrst law of thermodynamics is given by equation (5.16) for adiabatic changes and

remains the same in the Newtonian limit. This law relates P(ρ

)to(ρ

) in a one-parameter

EOS.

Before proceeding, we use the thermodynamic relation (5.63) for isentropic conﬁgura-

tions,

P = D

h, (15.7)

to rewrite the Euler equation (15.4)as

∂

+ v

=−D

h − D



. (15.8)

Here h is the speciﬁc enthalpy deﬁned by equation (5.5),

h = 1 +  + P/ρ

. (15.9)

See Marronetti and Shapiro (2003) for an exception.

15.1 Stationary ﬂuid solutions 509

In a Newtonian context, the enthalpy is usually deﬁned without the ﬁrst term, which

accounts for the contribution of the rest mass-energy,

h = 1 + h

Newt

. (15.10)

In general we will use the relativistic convention, but when considering Newtonian limits

it is sometimes useful to use h

Newt

In anticipation of our derivation of the corresponding relativistic equations we follow

an approach that is somewhat unconventional in a Newtonian context and express the time

derivatives of v

and ρ

in equations (15.8) and (15.6) in terms of a Lie derivative along

the helical Killing vector ξ

hel

(see equation 12.63). We adopt this approach as preparation

for our relativistic analysis in Section 15.1.2, which is greatly simpliﬁed by the formalism

introduced here. We start by writing ξ

hel

= t

+ k

. (15.11)

Here t

is a timelike vector that points “up” in a spacetime diagram, while k

is purely

spatial and describes rotations around the axis of rotation. We can write k

= 



∂

∂φ



, (15.12)

or, in Cartesian coordinates, as

= 

ijk



, (15.13)

where 

is aligned with the axis of rotation and measures the orbital angular velocity .

Together, t

and k

form the “corkscrew” shape of the helical Killing vector ξ

hel

We can now express the Lie derivative of v

hel

= ∂

+ L

= ∂

+ k

− v

, (15.14)

and that of ρ

hel

= ∂

+ L

= ∂

+ k

. (15.15)

We also write the ﬂuid velocity as

= k

+ V

, (15.16)

where V

now measures the ﬂuid velocity relative to k

. For a corotating ﬂuid, for example,

we must have V

= 0.

Exercise 15.1 Show that the Euler equation (15.8) can be written as

hel

−

+ D

) + V

− D

) =−D

h − D



, (15.17)

and the continuity equation (15.6)as

hel

+ V

+ ρ

= 0. (15.18)

510 Chapter 15 Binary neutron star initial data

Equations (15.17) and (15.18) are still completely general, since we have not specialized

yet to stationary solutions. However, at this point it is very easy to do so, since can simply

set the Lie derivatives of v

and ρ

along ξ

hel

to zero, in which case equation (15.17)

reduces to

−

+ D

) + V

− D

) =−D

h − D



. (15.19)

SincewealsohaveD

= 0 (which follows from equation 15.13), we can write equa-

tion (15.18) in the compact form

(ρ

) = 0. (15.20)

It is now clear that these equations simplify for two special types of ﬂuid ﬂow: corotational

ﬂow, where V

= 0, and irrotational ﬂow, where D

− D

= 0(i.e.,curl v = 0). We

will discuss these two cases separately.

Corotational binaries

For corotational, or synchronized, binaries we set V

= 0, and hence

= k

(corotational ﬂow) (15.21)

in equations (15.19) and (15.20). The continuity equation (15.20) is satisﬁed identically,

and does not provide any information. The Euler equations (15.19) reduce to

−

=−D

h − D



, (15.22)

which we can integrate once to ﬁnd the integrated Euler equation,

h + 

−

= C. (15.23)

Here C is a constant of integration. Squaring equation (15.13) to obtain

= 

, (15.24)

where ! measures the distance from the axis of rotation, we can write equation (15.23)as

Newt

+ 

−



= C

Newt

, (15.25)

wherewehaveintroducedC

Newt

= C − 1. This is a remarkable result: assuming corota-

tional ﬂuid ﬂow (15.21) we have reduced the equations of hydrodynamics, which in general

are a reasonably complicated set of coupled partial differential equations, to a single alge-

braic equation for the enthalpy h. Given a one-parameter EOS we can express the enthalpy

in terms of the density ρ

. Any density distribution that satisﬁes equation (15.25)andis

Lie dragged along v

= k

automatically satisﬁes the Euler equation (15.4) and the conti-

nuity equation (15.6), and is therefore a stationary solution to the Newtonian equations of

hydrodynamics.