Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

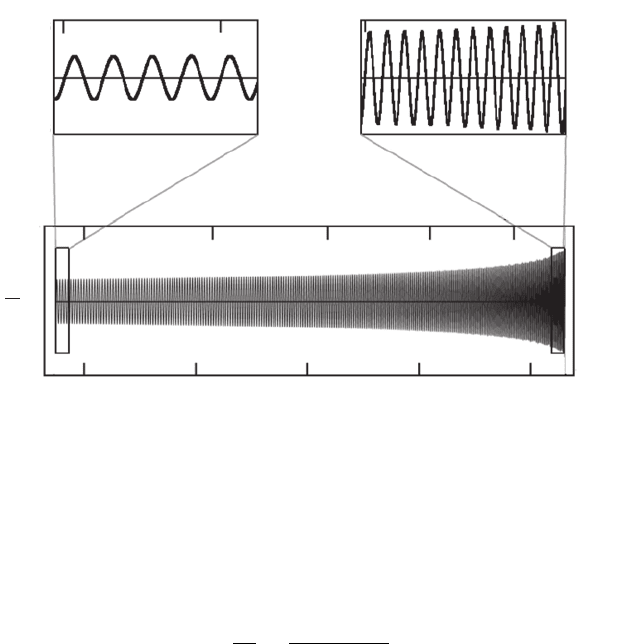
15.4 Quasiadiabatic inspiral sequences 531

0.06

0.07

−22

−10

−22

0.06

4.5

5.0 7.0 9.0

(( t− r

) / M

) × 10

−4

11.0 13.0

4.7 13.4

cyc

13.6

100 150 200 250 300

93 327 339

−0.06

−0.07

−0.06

Figure 15.7 The ﬁnal hundreds of cycles of the inspiral gravitational waveform measured along the axis of

rotation by a distant observer as a function of retarded time and cycle number for an irrotational binary neutron

star system. The numbers give the strain h for a binary of total rest mass M

= 2 × 1.5M



at a distance

= 100 Mpc. [From Duez et al. (2002).]

sequence of ﬁxed rest-mass yields the inspiral rate

ADM

/dt

ADM

/dr

. (15.83)

Integrating equation (15.83) then yields the separation as a function of time, r (t). For

example, equation (12.17) quotes the result for point-mass, Newtonian binaries radiating

in the quadrupole approximation. Given that we already know the gravitational waveform

as a function of r , we can then construct the entire gravitational wave train as a function of t.

Exercise 15.11 Use the results of exercise 12.3, together with equation (9.27),

to calculate the quasiadiabatic inspiral gravitational wave train for a Newtonian

binary. In particular, determine as functions of time the amplitude A(t) and the

phase (t) of the wave amplitude along the binary axis of rotation in the quadrupole

approximation,

= r

= A(t)cos(t), (15.84)

where r

is the distance to the source.

Duez et al. (2002) implemented a crude but illustrative version of such a scheme for

both corotational and irrotational relativistic binary inspiral.

In Figure 15.7 we show the

resulting quasiadiabatic gravitational wave train for irrotational binary inspiral.

See also Duez et al. (2001); Shibata and Ury

u (2001).

532 Chapter 15 Binary neutron star initial data

For a given separation, the gravitational wave luminosity dM

ADM

/dt is very similar for

corotational and irrotational models.

However, the ADM energy M

ADM

of corotational

models includes the spin kinetic energy of the individual stars, and as a consequence

ADM

decreases less for corotational binaries than for irrotational binaries as the binary

separation decreases. For corotational binaries |dM

ADM

/dr| is therefore smaller than for

irrotational binaries, so that, according to (15.83), the inspiral of corotational binaries

proceeds faster than that of irrotational binaries.

Finally, we can construct the entire gravitational wave train by matching the quasiadia-

batic gravitational wave train to the waveform arising from plunge and merger phases.

Calculating the waveform emitted during the highly dynamical plunge and merger phases

is the focus of Chapter 16.

This result is not surprising, since the gravitational wave emission is dominated by the matter mass density, which is

fairly similar for corotational and irrotational binaries, while the matter current density is less important.

Figure 6 in Duez et al. (2002) exhibits such a match.

Binary neutron star

evolution

Binary neutron stars have always been of great interest to relativists and astrophysicists.

Binary neutron stars are known to exist. Approximately a half-dozen have been identiﬁed

to date in our own galaxy, and, for some of these, general relativistic effects in the binary

orbit have been measured to high precision.

The discovery of the ﬁrst binary pulsar, PRS

1913 + 16, by Hulse and Taylor (1975), led to the observational conﬁrmation of Einstein’s

quadrupole formula for gravitational wave emission in the slow-motion, weak-ﬁeld regime

of general relativity. The inspiral and coalescence of binary neutron stars is one of the most

promising scenarios for the generation of gravitational waves detectable by laser interfer-

ometers. With the construction of the ﬁrst of these interferometers completed, and planned

upgrades already scheduled, it is of growing urgency that theorists be able to predict the

gravitational waveform emitted during the merger of the two stars. The low-frequency

inspiral waveform is emitted early on, before tidal distortions of the stars become impor-

tant, and it can be calculated fairly accurately by performing high-order post-Newtonian

expansions of the equations of motion for two point masses.

The high-frequency coales-

cence waveform is emitted at the end, during the epoch of tidal distortion, disruption and

merger, and it requires the combined machinery of relativistic hydrodynamics (or MHD)

and numerical relativity. These tools are necessary to determine not only the waveform

in the strong-ﬁeld regime but also the ﬁnal fate of the merged remnant. One of the key

issues is determining whether a merged remnant collapses to a black hole immediately

after coalescence (“prompt collapse”) or instead forms a transient, dynamically stable, dif-

ferentially rotating, hypermassive star that only later undergoes collapse due to dissipative

secular effects (“delayed collapse”). These different outcomes will leave distinguishing

imprints on the late-epoch gravitational waveform.

Gravitational wave generation may be only one of several observable consequences of

binary neutron star merger. Gamma-ray bursts (GRBs) may be another, as there are many

theoretical models for which the coalescence of a binary neutron star provides the energy

source for a GRB.

Binary neutron stars, as well as black hole-neutron star binaries, are

currently invoked to explain one class of GRBs, namely the short, hard GRBs that are

characterized by their short duration and hard radiation spectrum. Currently favored

are scenarios in which the merger leads to the formation of a rapidly rotating black

Taylor and Weisberg (1989); Stairs et al. (1998).

See Chapter 9.4 and Appendix E for discussion and references; see also Chapter 12.1 for an overview of binary inspiral.

Paczynski (1986); Eichler et al. (1989); Narayan et al. (1992); Ruffert and Janka (1998).

533

534 Chapter 16 Binary neutron star evolution

hole surrounded by a torus of debris, wherein the energy of the burst originates from either

ν ¯ν annihilation or from the rotational energy of the black hole.

In addition, decompressed

nuclear matter ejected during binary neutron star coalescence may provide an explanation

for the observed abundance of r-process nuclei.

Relativistic binary systems, like binary black holes, neutron stars and black hole-neutron

stars, pose a fundamental challenge to theorists. Indeed, the two-body problem has been one

of the most outstanding problems in classical general relativity. Tackling this problem in its

many incarnations represents one of the most important applications of numerical relativity,

and providing solutions constitutes one of numerical relativity’s greatest triumphs.

16.1 Peliminary studies

The earliest computational work on binary neutron stars consisted of simulations of head-

on collisions of identical stars.

The restriction to head-on collisions enables the calculation

to be performed in axisymmetry (i.e., 2 +1 dimensions), which requires far fewer com-

putational resources than simulations in full 3 + 1 dimensions. However, astrophysical

scenarios that lead to binary neutron star collisions most likely involve inspiral in a quasi-

circular orbit, since gravitational radiation will circularize a bound, eccentric binary orbit

well before stellar contact.

Newtonian studies of instabilities in binary systems in close circular orbit, and the

nonlinear evolution of unstable binaries all the way to complete coalescence, have been

the subject of many early investigations. The classical work by Chandrasekhar

for equi-

librium binaries composed of incompressible ﬂuids has been extended to compressible

ﬂuids.

These analytic studies identify the existence of dynamical and secular instabilities

in sufﬁciently close systems. They even give rise to an approximate set of hydrodynamical

evolution equations, incorporating viscosity and gravitational radiation reaction, that can

be integrated to model binary inspiral and the corresponding gravitational radiation wave-

forms.

Although these simpliﬁed analytic studies can give appreciable physical insight

into tidal effects and global ﬂuid instabilities, fully numerical calculations are essential for

establishing rigorous stability limits for close binaries and for following the nonlinear evo-

lution of unstable systems all the way to complete coalescence, even in Newtonian theory.

See Piran (2005) for review and references.

Symbalisty and Schramm (1982); Eichler et al. (1989); Rosswog et al. (1998).

For early overviews and references, see, e.g., Rasio and Shapiro (1999); Font (2000); Baumgarte and Shapiro (2003c).

For Newtonian simulations, see Gilden and Shapiro (1984); for relativistic simulations, see Wilson (1979); Abrahams

and Evans (1992); Jin and Suen (2007), and references therein.

Peters (1964); see Chapter 12.1.

Chandrasekhar (1969).

Lai et al. (1993a, 1994a,c); Taniguchi and Nakamura (2000a,b).

Lai et al. (1994c); Lai and Shapiro (1995b), and references therein. In the triaxial ellipsoid treatment adopted here, the

hydrodynamical equations in 3 + 1 reduce to ordinary differential equations. The treatment is exact for incompressible

ﬂuids orbiting in tidal gravitational ﬁelds. See also Carter and Luminet (1983, 1985); Luminet and Carter (1986);

Kochanek (1992a,b); Kosovichev and Novikov (1992).

16.2 The conformal ﬂatness approximation 535

Given the absence of any underlying spatial symmetry in the problem, these calculations

must be done in 3 + 1 dimensions.

Newtonian simulations of coalescing neutron stars have been performed by numerous

investigators employing a variety of numerical methods and emphasizing different aspects

of the problem. Nakamura and collaborators

were the ﬁrst to perform hydrodynamic sim-

ulations of binary neutron star (sometimes abbreviated NSNS) coalescence from circular

orbits. They used an Eulerian ﬁnite-difference code for the hydrodynamics and focused on

gravitational wave generation. Rasio and Shapiro

employed the Lagrangian SPH method

(see Chapter 5.2). They focused on determining the stability properties of initial binary

models in strict hydrostatic equilibrium and calculating the emission of gravitational waves

from the coalescence of unstable binaries. Many of their results were conﬁrmed by New

and Tohline,

who used completely different numerical methods but also focused on sta-

bility questions, and by Zhuge et al.,

who also used SPH. The later group also explored

the dependence of the gravitational wave signals on the initial neutron star spins. Davies

et al.,

who used SPH, and Ruffert et al.

who employed a high-resolution shock-

capturing (HRSC) hydrodynamics scheme, incorporated a simple treatment of the nuclear

physics in their hydrodynamic calculations, motivated by models of gamma-ray bursts and

the ejection of r-process nuclei.

16.2 The conformal ﬂatness approximation

One of the ﬁrst approaches used to simulate binary neutron star coalescence in general

relativity was the conformal ﬂatness approximation, pioneered by Wilson and Mathews.

In this approach, one assumes that the dynamical degrees of freedom of the gravitational

ﬁeld, i.e., the gravitational radiation, play a negligible role in determining the dynamical

behavior or structure of the neutron stars. Simplifying the spacetime to reduce radiative

inﬂuences, one sets the initial spatial metric to be conformally ﬂat, γ

= ψ

, so that the

spacetime metric takes the form

=−α

+ ψ

(dx

+ β

dt)(dx

+ β

dt). (16.1)

One further assumes that the spatial metric remains conformally ﬂat at all times,an

approximation that greatly simpliﬁes the resulting ﬁeld equations. For example, in the

ADM scheme, the traceless part of equation (2.134) then has to vanish, which, according

to equations (3.92) and (3.93), yields

2α

(Lβ)

. (16.2)

See Nakamura and Oohara (1991) and references therein.

Rasio and Shapiro (1992, 1994, 1995).

New and Tohline (1997).

Zhuge et al. (1994, 1996).

Davies et al. (1994); Rosswog et al. (1999).

Ruffert et al. (1996); Ruffert and Janka (1998).

Wilson and Mathews (1989, 1995). See also Isenberg (1978); Wilson et al. (1996).

536 Chapter 16 Binary neutron star evolution

Here A

is the traceless part of the extrinsic curvature, and the vector gradient L is deﬁned

in (3.50). We will discuss the validity of this approximation below.

The resulting equations can be derived in complete analogy to our treatment of the

conformal thin-sandwich decomposition in Chapter 3.3. In particular, we can substitute

equation (16.2) into the momentum constraint (2.133) to yield an equation for the shift

vector β

. The conformal factor ψ can be found from the Hamiltonian constraint (2.132),

and, adopting maximal slicing with K = 0 = ∂

K (see Chapter 4.2), we can also obtain

an equation for the lapse function α. With the conformal rescaling relation (3.35)for A

these equations then reduce to the thin-sandwich equations (3.116)–(3.118) with

R = 0

and ﬂat-space differential operators,



ﬂat

ψ =−

−7

− 2πψ

ρ (16.3)

(

ﬂat

β)

= 2

(αψ

−6

) + 16παψ

(16.4)



ﬂat

(αψ) = αψ



−8

+ 2πψ

(ρ + 2S)



. (16.5)

This coupled system now completely determines the metric (16.1).

All unknowns in the metric (16.1) are determined by elliptic equations, and in this

sense all dynamical degrees of freedom have been removed from the gravitational ﬁelds.

In this approach, one solves an initial value problem at each instant of time, as opposed

to dynamically evolving the gravitational ﬁelds. While one may be concerned about the

accuracy of this approximation (see below), it greatly simpliﬁes the ﬁeld equations and

allowed Wilson and Mathews (1995) to perform some of the ﬁrst relativistic simulations

of binary neutron stars. In this approach, the time step is limited by the matter sound speed

and not the light speed, since there are no dynamical ﬁeld equations. Hence the time step

can be much larger than in fully self-consistent algorithms. In their simulations, Wilson

and Mathews (1995) solved equations (3.116)–(3.118)forthemetric(16.1) simultaneously

with Wilson’s formulation of the relativistic equations of hydrodynamics, equations (5.12)–

(5.14). In their approach, at each timestep one ﬁrst evolves the matter variables, and

then solves the ﬁeld equations for the metric, with the new matter distribution used to

compute the source terms. If desired, the gravitational wave emission can then be estimated

a posteriori using the quadrupole formula or some other low-order expansion scheme.

Alternatively, the matter proﬁle computed via the conformal ﬂatness approximation can

be used to calculate the source terms in the full dynamical ﬁeld equations to determine the

gravitational radiation as a perturbation. The later approach has already been discussed in

Chapter 15.4.

A useful computational check of a code that adopts the conformal ﬂatness approxima-

tion is provided by the fact that the conformally ﬂat evolution equations maintain strict

stationary equilibrium for initial data satisfying the conformal thin-sandwich equations

See exercise 3.17 for an expansion of the differential operators into partial derivatives.

16.2 The conformal ﬂatness approximation 537

for the metric coupled to the stationary equilibrium equations for the matter. These are the

initial data we obtained for relativistic binaries in circular equilibrium in Chapter 15.1.1.

Exercise 16.1 Consider a corotating, circular equilibrium binary constructed as

in Chapter 15.1.1 using the conformal thin-sandwich approximation coupled to

the integrated Euler equation (15.46). Conﬁrm that these initial data are strictly

conserved in the the conformal ﬂatness approximation. Speciﬁcally, show that the

conformal thin-sandwich initial value solution provides a stationary solution to

the hydrodynamic matter evolution equations (5.12), (5.13)and(5.14), coupled to

the metric equations (16.3)–(16.5). Use the fact that for corotating binaries, the ﬂuid

velocity satisﬁes v

= 0 in the corotating frame.

Hint: It also may be helpful to use the relativistic Gibbs–Duhem relation dh =

dP/ρ

Of course, in full general relativity, binaries constructed from such initial data are only

in quasiequilibrium, as they undergo inspiral due to the emission of gravitational radiation.

To mimic inspiral in the conformal ﬂatness approximation, a post-Newtonian gravitational

radiation-reaction potential

is sometimes added in the Euler equation.

Validity of the conformal ﬂatness approximation

In Chapter 3 we found that conformal ﬂatness greatly simpliﬁes the initial value equations.

Here we have seen that it greatly simpliﬁes the evolution treatment as well. It is important,

however, to appreciate that the two treatments are very different in nature. For the con-

struction of initial data, the assumption of conformal ﬂatness still leads to exact solutions

to Einstein’s constraint equations, and therefore does not represent an approximation in

this sense.

The true dynamical evolution of such initial data, however, will generally

lead to a spatial geometry that does not remain conformally ﬂat. Assuming conformal

ﬂatness during a dynamical simulation therefore yields solutions that, in general, are only

approximate spacetime solutions to Einstein’s equations.

The conformal ﬂatness approximation has been used frequently to model relativistic

systems in which gravitational radiation plays a minimal role in the structure and evolution

of a system on the time scales of interest. This is certainly the case for spherical spacetimes

(e.g., as in spherical stellar collapse) for which the formalism is exact. It is also applicable,

albeit approximately, to quasiequilibrium binary systems in circular orbit over a few orbital

periods.

In Chapter 3 we found that the dynamical degrees of freedom of the gravitational

ﬁelds can be identiﬁed with parts of the conformally-related spatial metric and the

See equation (1.50) and Chapter 9.1.1, as well as, e.g., Burke (1971)orMisner et al. (1973), Chapter 36.8, for a

discussion of the radiation-reaction potential.

Conformally ﬂat initial data, even though they constitute exact solutions to Einstein’s constraint equations, may

not represent conﬁgurations that are astrophysically realistic. It is in this sense they are sometimes referred to as

approximations.

538 Chapter 16 Binary neutron star evolution

transverse-traceless part of the extrinsic curvature. This suggests that the assumptions

of conformal ﬂatness and the vanishing of

may indeed “minimize the gravitational

radiation content” of a spatial slice . This argument cannot be strictly true, however; it

does not even hold for single rotating black holes. Rotating Kerr black holes, which are

stationary and do not emit any gravitational radiation, are not conformally ﬂat.

Similarly,

conformally-ﬂat models of rotating black holes that are constructed in the Bowen–York

formalism do contain gravitational radiation.

For rapidly rotating, isolated neutron stars in stationary equilibrium, the restriction to

conformal ﬂatness introduces an error of at most a few percent, and the error is this

large only for the most relativistic and rapidly rotating conﬁgurations.

Similarly, small

differences exist between conformally ﬂat binary neutron star models and binary models

constructed under different assumptions.

These small deviations are not surprising, since

differences between a conformally ﬂat metric and the “correct” metric already appear at

second post-Newtonian order,

and thus are on the order of a few percent for neutron stars.

To gauge the importance such an error, it should be compared with other approximations

and errors made in the calculations, including ﬁnite resolution error, the treatment of outer

boundaries, uncertainties in the equation of state, and the effect of neglecting other physical

processes like neutrino transport or magnetic ﬁelds in the simulation.

To calibrate the conformal ﬂatness approximation it is useful to compare how well it

performs in comparison to fully relativistic calculations. Shibata and Sekiguchi (2004)

have performed axisymmetric simulations of rotating stellar core collapse to a neutron star

in full general relativity, using the BSSN scheme to integrate the gravitational ﬁeld equa-

tions. They ﬁnd that the evolution of the central density during the collapse, bounce and

formation of the protoneutron star agrees well with the evolution found by Dimmelmeier

et al. (2002a,b), who use the conformal ﬂatness approximation to simulate the same prob-

lem. Both groups employ an HRSC scheme to integrate the relativistic ﬂuid equations

for the matter. Both groups computed gravitational waves using the quadrupole approxi-

mation, although they adopted slightly different forms for the quadrupole formula. Their

waveforms are in good qualitative agreement, but exhibit some quantitative differences.

The differences in their adopted quadrupole formulae are likely responsible for most of

At least slices of constant Boyer–Lindquist time are not conformally ﬂat, nor are axisymmetric foliations that smoothly

reduce to slices of constant Schwarzschild time in the Schwarzschild limit; Garat and Price (2000).

Brandt and Seidel (1995a,b, 1996); Gleiser et al. (1998); Jansen et al. (2003).

Cook et al. (1996).

Usui et al. (2000); Usui and Eriguchi (2002).

Rieth and Sch

afer (1996).

Shibata and Sekiguchi (2004) had to use the quadrupole approximation to compute waveforms since the wave

amplitudes were too small (< 10

) to be extracted accurately from the metric data with their uniform spatial grid

of 2500 × 3 × 2500 zones. The formula for the quadrupole moment is not deﬁned uniquely in strong-ﬁeld general

relativity; different forms of the integrand all have the same Newtonian limit. The formula adopted by Shibata and

Sekiguchi (2004) was calibrated against fully relativistic waveforms calculated for highly oscillating and rapidly

rotating neutron stars of high compaction. The quadrupole formula wave amplitudes were found to be reliable to

within 10% error, with waveform phase errors considerably smaller.

16.2 The conformal ﬂatness approximation 539

the discrepancy, suggesting that the conformal ﬂatness approximation is quite adequate

for handling many features of stellar collapse to neutron stars.

Exercise 16.2 (a) Show from the quadrupole formula that the gravitational wave

amplitude of the + mode in axisymmetric spacetimes may be obtained from

ret

) −

ret

)

sin

θ, (16.6)

where the symmetry axis is along z, I

is the quadrupole moment, r is the distance

to the observer, θ is the polar angle of the observer and t

ret

is retarded time. (What

can you say about the × mode in axisymmetry in the quadrupole approximation?)

(b) Deﬁne the quadrupole moment as in Shibata and Sekiguchi (2004):

≡



∗

x, (16.7)

where ρ

∗

≡ γ

1/2

D = αu

1/2

. Use the continuity equation (5.12) to show that

the ﬁrst time derivative of I

can be obtained from



∗

+ x

x. (16.8)

Hence argue that to compute

in equation (16.6), only one numerical time deriva-

tive of the data is required provided equation (16.8) is used, which is much more

reliable than using equation (16.7) and taking two numerical derivatives.

This suggesion is strengthened considerably by the relativistic simulations of rotating

stellar core collapse in both 3 + 1 and 2 + 1 (axisymmetry) by Ott et al. (2006), who also

incorporated more detailed microphysics in their modeling.

They compared fully general

relativistic evolution using a BSSN scheme with a treatment adopting conformal ﬂatness

and focused on gravitational wave emission from the rotating collapse, core bounce and the

early post-bounce phases. The waveforms computed by extracting the metric data directly in

the fully relativistic simulation closely match those computed from the quadrupole formula

in the simulation that adopts conformal ﬂatness. This suggests that the conformal ﬂatness

approximation is sufﬁciently accurate to handle the core-collapse supernova problem, at

least when the outcome is a neutron star.

As we emphasized above, the conformal ﬂatness approximation is, in general, incon-

sistent with Einstein’s evolution equations. Miller and Suen (2003) have attempted to

calibrate this error for the inspiral of binary neutron stars. To do so, they compute the

Bach tensor B

(see equation 3.15), which vanishes if and only if the spatial metric γ

is conformally ﬂat.

To construct a diagnostic that measures departure from conformal

This trick was ﬁrst pointed out by Finn and Evans (1990).

Ott et al. (2006) employ a ﬁnite-temperature equation of state (EOS) and an approximate treatment of deleptonization

during collapse.

See the related discussion in Chapter 3.1.2; note that Miller and Suen (2003) use a conformal rescaling that is different

from that in equation (3.15).

540 Chapter 16 Binary neutron star evolution

ﬂatness they compute the matrix norm |B

and normalize this quantity to the magnitude

of the covariant derivative of the 3-Ricci tensor, B ≡|B

|/(D

)

1/2

. They then

integrate this quantity across a star and obtain a rest-mass weighted average of B, denoted

by B. Miller and Suen (2003) evaluate the diagnostic B for a binary system of identical,

corotating neutron stars, modeled initially as relativistic polytropes with index n = 1and

evolved adiabatically with adiabatic index  = 2. They normalize their polytropic equation

of state so that the maximum ADM mass of a spherical, static star is 1.79M



, whereby the

maximum rest mass M

is 1.97M



. They treat binaries with stellar rest masses of 1.49M



approximately 75% of the maximum mass; in isolation, static stars with this rest mass have

an ADM mass of about 1.4M



. They begin their simulations with quasiequilibrium bina-

ries constructed in the conformal thin-sandwich formalism, assuming conformal ﬂatness

so that B vanishes initially. They treat close binaries orbiting at several different initial

separations, including an initial separation close to the ISCO. In all cases B increases

from zero to a maximum value in a fraction of an orbital period, and then begins to decay.

The maximum value is larger for tighter binaries, but is never more than a few percent,

in agreement with our rough estimate above. Even for the tightest orbit, where the spatial

geodesic separation between the density maxima in the two stars is l/M

= 23.44 and the

orbital frequency is M

= 0.01547, the value never rises above 5% before it begins to

decay. This ﬁnding helps quantify the degree to which the conformal ﬂatness approxima-

tion provides a reasonable model for the spacetime of a relativistic binary neutron star, at

least during the inspiral phase.

Numerical results

The pioneering simulations of binary inspiral by Wilson and his collaborators introducing

the conformal ﬂatness approximation have been followed by several other treatments of

increasing sophistication.

One of the earliest was by Oechslin et al. (2002), who employed

a Lagrangian SPH hydrodynamics code with a multigrid elliptic solver to handle the metric

equations, and adopted corotating initial conﬁgurations. While these conﬁgurations are

believed to be unphysical for neutron stars,

these simulations conﬁrmed earlier SPH

simulations in post-Newtonian (PN) gravitation

that suggested that relativistic effects

suppress mass loss during merger.

The matrix norm of the tensor B

is deﬁned as the square root of the largest eigenvalue of B

The original version of Wilson and Mathews (1995) contained a mathematical error, pointed out by Flanagan (1999),

which is now believed to be mainly responsible for the spurious ﬁnding of a “crushing” instability that triggers the

collapse of the neutron stars prior to merger; see our discussion in Chapter 15.2. Numerous earlier analyses, including

the post-Newtonian dynamical simulations of Shibata et al. (1998), had cast considerable doubt on the existence of a

“crushing” instability.

Viscous stresses are thought to be too weak to maintain tidal synchronization in binary neutron stars; Bildsten and

Cutler (1992); Kochanek (1992a); see Chapter 15.1.

Faber and Rasio (2002).