Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

16.2 The conformal ﬂatness approximation 541

Faber et al. (2004) subsequently performed SPH simulations in the conformal ﬂatness

approximation using a spectral elliptic solver in spherical coordinates

for the metric equa-

tions. They considered the adiabatic evolution and merger of equal-mass relativistic binary

polytropes with n = 1and = 2. For initial data they employed the quasiequilibrium,

irrotational binary models of Taniguchi and Gourgoulhon (2002), which are constructed

using the conformal thin-sandwich formalism. Faber et al. (2004) consider binaries whose

members each have rest mass M

= 0.146 in units where the polytropic gas parame-

ter K = 1(i.e.,

= 0.146). At inﬁnite separation, such a star has a total mass-energy

(i.e., ADM mass) equal to M = 0.136 and a compaction M/R = 0.14. (For compari-

son, the maximum-mass conﬁguration for a static n = 1 polytrope has M

max

= 0.180

and M

max

= 0.164.) The binary proﬁles form a cusp slightly within an orbital radius

= 19.9, inside of which quasiequilibrium, irrotational, circular-orbit solutions do

not exist for this EOS. Here M

≡ µ

3/5

2/5

= M/2

1/5

is the “chirp mass” at large sep-

aration, where M

is the total (ADM) mass-energy of the system at large separation and

µ ≡ M

is the reduced (ADM) mass.

Typical runs employ approximately 10

SPH particles to solve the hydrodynamic equa-

tions and three spheroidal computational domains around each star to evaluate the ﬁeld

equations. As a test, Faber et al. (2004) demonstrate that the binaries remain dynami-

cally stable and maintain circular equilibrium for all separations up to cusp formation. By

inserting an approximate PN radiation-reaction potential term in the Euler equation they

trigger a small inward spiral motion and follow the complete coalescence of a binary from

just outside the cusp radius through merger, remnant formation and ringdown. They ﬁnd

that mass loss is highly suppressed, but that the massive remnant is dynamically stable

against gravitational collapse because of its strong differential rotation. In other words,

the remnant settles into an equilibrium hypermassive neutron star like those discussed

in Chapter 14. Snapshots of the merger scenario are depicted in Figures 16.1 and 16.2.

The rotation proﬁle of the hypermassive merger remnant is plotted in Figure 16.3.The

gravitational radiation waveforms, calculated from the quadrupole formula, are shown in

Figure 16.4.

Exercise 16.3 Assume that each neutron star in the binary system shown in Fig-

ures 16.1–16.4 has a rest mass of M

= 1.5M



. Compute the ADM mass, chirp

mass M

and stellar radius R at large separation. Convert the length, time, and

angular velocity scales plotted in the ﬁgures to physical units. Evaluate the maxi-

mum amplitude of the waveform shown in Figure 16.4 if the binary were located in

the Virgo cluster (d ≈ 20 Mpc, where 1 Mpc = 3.09 × 10

cm).

One of the most extensive sets of binary neutron star merger calculations based on

the conformal ﬂatness approximation to Einstein’s ﬁeld equations is that of Oechslin et al.

(2007). Like Faber et al. (2004), they employ a relativistic SPH code for the hydrodynamics,

The LORENE numerical libraries, developed by Grandcl

ement et al. (2001) and publically available online at

http://www.lorene.obspm.fr were used in these simulations.

542 Chapter 16 Binary neutron star evolution

10 10

t/M

=500

t/M

=750

t/M

= 850

x/M

y/M

t/M

0 0

−10

−10 −10

−20

−20−20

20 20

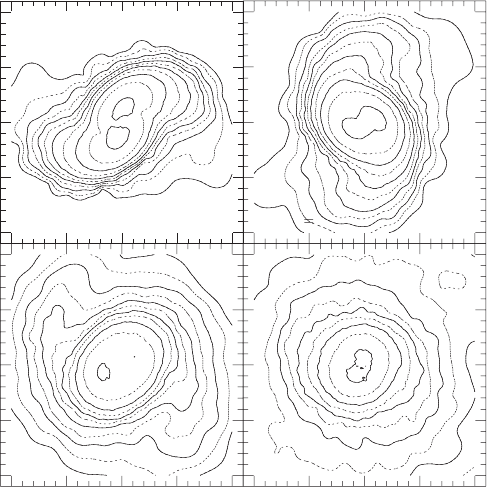
Figure 16.1 The evolution of an equal-mass, irrotational binary neutron star system in the conformal ﬂatness

approximation, as viewed in the orbital plane. The simulation begins just outside the orbital separation where a

cusp develops and continues through the merger and formation of a remnant. Density contours shown here are

logarithmically spaced, two per decade, ranging from M

∗

= 10

−6.5

to 10

−1

. A signiﬁcant tidal lag angle

develops at t/M

= 500, followed by an “off-center” collision. This process leads to the formation of a vortex

sheet and a small amount of matter ejection by t/M

= 850. [From Faber et al. (2004).]

but unlike Faber et al. (2004), they include artiﬁcial viscosity to handle shocks (see

Chapter 5.2.1). They solve the metric equations with the help of a multigrid solver and

employ approximately 120 000 SPH particles in their simulations. Most signiﬁcantly,

they consider the effect of varying the nuclear EOS, the neutron star masses and the

neutron star spins.

Oechslin et al. (2007) supplement their treatment by adding a small,

nonconformally ﬂat gravitational radiation back-reaction contribution to the metric,

which is only important during the inspiral phase before the plunge.

They ignore neutrino

transport by arguing that any back-reaction of the neutrino emission on the matter is

Oechslin et al. (2007) impose the irrotational spin condition, as well as their other choices for the initial spin, only

approximately. However, when they compare their initial models to corresponding models obtained via the conformal

thin-sandwich scheme, they ﬁnd deviations in global quantities like the total angular momentum J and orbital angular

velocity  to be small, of order 1%.

They adopt the 3.5 PN prescription of Faye and Sch

afer (2003).

The merger and postmerger phases are found to depend very weakly on the inspiral dynamics.

16.2 The conformal ﬂatness approximation 543

t/M

= 970

t/M

= 1020

t/M

= 1220

x/M

y/M

t/M

= 920

−10

−20

Figure 16.2 The advanced evolution of the merger depicted in Figure 16.1; labels are the same as in that ﬁgure.

A dense remnant forms in the center of the system, surrounded by a thin halo. Some ellipticity is seen shortly

after the merger, but the system quickly relaxes toward a spheroidal, hypermassive equilibrium conﬁguration,

with maximum density in the center of the system. [From Faber et al. (2004).]

negligible on the 10 ms (dynamical) time scales of interest here. They consider several

models for the ﬁnite-temperature nuclear EOS, including the “hard” EOS of Shen et al.

(1998a,b), which gives a cold, static, maximum neutron star mass of about 2.2M



,and

the“soft”EOSofLattimer and Swesty (1991), for which the maximum mass is about

1.8M



. The simulations show that the dynamics and the ﬁnal outcome of the merger

depend sensitively on the EOS and the binary parameters. For example, Oechslin et al.

(2007) ﬁnd that with the soft EOS the remnant collapses to a black hole either immediately

or within a few dynamical timescales after merger, while for all other EOSs, the remnant

does not collapse but instead forms a hypermassive equilibrium conﬁguration. The mass of

the low-density torus that forms around the black hole is larger for unequal-mass systems

(reaching 0.3M



for a mass ratio of 0.55), large initial neutron stars and for neutron star

spin states that result in a larger total angular momentum. The characteristic temperatures

achieved in the torus are 3–10 MeV, depending on the degree of shear at the collision

interface; the shear, in turn, depends on the initial spins. Only about 10

−3

to 10

−2

of the

total rest mass escapes from the system.

544 Chapter 16 Binary neutron star evolution

01020

cyl

t /M

= 1220

Ω

0.04

0.02

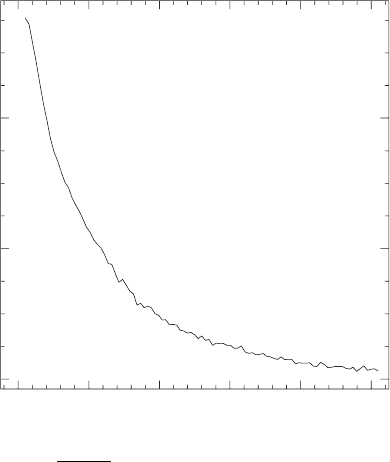
Figure 16.3 Angular velocity of the hypermassive merger remnant in Figure 16.2 at t/M

= 1220, shown as a

function of cylindrical radius, r

cyl

≡



+ y

. The remnant exhibits strong differential rotation, with the

highest angular velocity in the center, decreasing monotonically with radius. It is this differential rotation that

supports the hypermassive remnant against collapse. [From Faber et al. (2004).]

From these simulations Oechslin and Janka (2006) suggest that binary neutron star

mergers may be the origin of short-hard gamma-ray bursts (GRBs). Previous simulations

indicated that insufﬁcient energy is liberated during the highly dynamical phase of the

merger event to account for the observed energies. Moreover, the possibility that a GRB

is triggered during the neutrino emitting, pre-collapse lifetime of the hypermassive rem-

nant is also doubtful, because the high mass-loss rates in the neutrino-driven wind will

likely quench the propagation of gamma-rays (the “baryon loading” problem). Instead,

Oechslin and Janka (2006) propose that the bursts could be powered by neutrino-

antineutrino annihilation in the hot gas in the torus surrounding the black hole remnant.

In particular, the measured GRB energies and durations lead to estimates for the accreted

mass and accretion rate that are compatible with their theoretical estimates derived from

their simulation data. Their model is not very different from the scenario proposed by

Shibata et al. (2006a), based on their general relativistic MHD simulations of the evolu-

tion and collapse of a magnetized hypermassive star and the black hole-magnetized torus

Ruffert et al. (1996).

16.3 Fully relativistic simulations 545

0.4

0.2

0 500

t/M

1000

0.4

0.2

−0.2

−0.4

−0.2

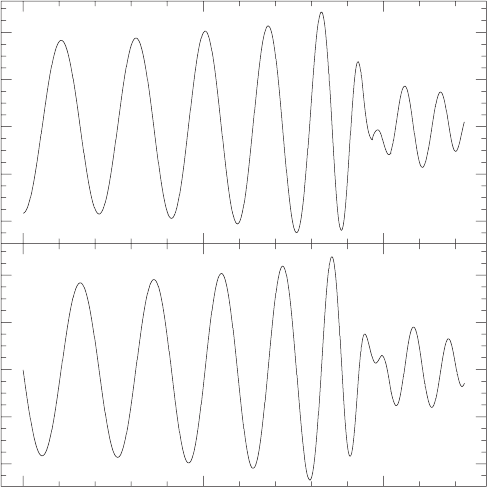
Figure 16.4 The GW signal in the h

and h

polarizations for the merger depicted in Figures 16.1 and 16.2 as

seen by an observer situated along the vertical axis. The amplitude is scaled with the distance of the observer,

d/M

. A chirp signal is followed by a modulated ringdown spike. The modulation is caused by the alignment

between quadrupole deformations in the inner regions of the remnant core and and those at larger radius. [From

Faber et al. (2004).]

conﬁguration that results.

While the origin of GRBs is far from resolved, the key point

is that numerical relativity is now sufﬁciently mature to address the issue.

16.3 Fully relativistic simulations

Several groups have launched efforts over the years to solve the full set of Einstein’s ﬁeld

equations self-consistently with the equations of relativistic hydrodynamics to model the

merger of binary neutron stars.

Many of the most advanced and detailed simulations to

date have been performed by Shibata and his collaborators.

These simulations represent

a major achievement of numerical relativity and demonstrate the degree to which fully

See Chapter 14.2.5.

See, e.g., Oohara and Nakamura (1999); Baumgarte et al. (1999); Font et al. (2000, 2002).

Shibata (1999a); Shibata and Ury

u (2000, 2002); Shibata et al. (2003b); Shibata et al. (2005); Shibata (2005); Shibata

and Taniguchi (2006).

546 Chapter 16 Binary neutron star evolution

relativistic calculations of binary neutron stars have advanced. We will summarize some

of the highlights of these calculations below.

Equal-mass binaries

The ﬁrst truly successful simulations of binary neutron star mergers in full general relativ-

ity were those of Shibata and Ury

u (2000), which used a computational scheme developed

and tested earlier by Shibata (1999a). The original scheme employed the BSSN formula-

tion of Einstein’s equations to evolve the ﬁeld equations (see Chapter 11.5) and the Wilson

form of the equations of relativistic hydrodynamics, equations (5.12), (5.14) and (5.19).

The stars are constructed using an n = 1 polytropic EOS; the matter is assumed to evolve

adiabatically according to a -law EOS with  = 2. The transport terms in the hydrody-

namics equations are handled by a second-order van Leer algorithm.

Artiﬁcial viscosity

is used to capture shocks, as in equation (5.24). Shibata and Ury

u (2000) employ “approx-

imate maximal slicing” (Chapter 4.2) to specify the lapse α and “approximate minimal

distortion” (Chapter 4.5) to determine the shift β

. They also add a radial component to

the shift vector to avoid grid stretching in collapse situations (see the discussion at the very

end of Chapter 4.5). Most of their simulations in this study used a ﬁxed uniform grid with

233 × 233 × 117 grid points in the x–y–z directions, respectively, and assumed reﬂection

symmetry across the equatorial (orbital) plane at z = 0.

As initial data, Shibata and Ury

u (2000) prepared equal-mass polytropic (n = 1) mod-

els of binary neutron stars in quasiequilibrium with both corotational (see Chapter 15.2)

and irrotational (see Chapter 15.3) velocity proﬁles. For both velocity proﬁles they gen-

erated three different models with individual stellar masses ranging from about 70% to

100% of the maximum allowed mass of nonrotating stars in isolation. For corotational

models, they adopted contact models (z

= 0 in the parametrization of Chapter 15.2)

as initial data, which are fairly close to the ISCO. As we discussed in Chapter 15.3,

irrotational sequences terminate at cusp formation, which is still outside of the ISCO.

Shibata and Ury

u (2000) therefore adopted the cusp model as initial data, and induced

collapse by artiﬁcially reducing the angular momentum by about 2.5%. Since irrotational

velocity proﬁles are probably more realistic, we will discuss their models (I1), (I2) and

(I3) for irrotational binaries. The initial data for these three models are summarized in

Table 16.1.

The simulation for model I1 is for a binary of total rest mass

= 0.261.

The angular

momentum of the initial data is J/M

= 0.98, where M is the total ADM mass, and is

hence smaller than the Kerr limit J/M

= 1. We show snapshots of density contours in

Figure 16.5.

van Leer (1977).

More information can be found in Table 1 of Shibata and Ury

u (2000).

We have converted the units of Shibata and Ury

u (2000) into the same dimensionless (“barred”) units adopted earlier

in this book, corresponding to setting the polytropic gas constant K = 1.

16.3 Fully relativistic simulations 547

Table 16.1 Summary of the initial data for the coalescence

simulations of irrotational binary neutron stars obeying an n = 1

polytropic EOS. Here

M and J are the total rest mass, ADM

mass and angular momentum of the binary. In these dimensionless

units, the maximum allowed rest mass of an isolated, nonrotating star

max

= 0.180. [Table adapted from Shibata and Ury

u (2000).]

Model ¯ρ

max

MJ/M

remnant

I1 0.0726 0.261 0.242 0.98 neutron star

I2 0.120 0.294 0.270 0.93 black hole

I3 0.178 0.332 0.301 0.88 black hole

In contrast to the coalescence of corotational binaries, no signiﬁcant spiral arms form

during the merger of irrotational stars, and hardly any matter is ejected. Nevertheless, the

remnant settles down to an equilibrium neutron star and does not collapse to a black hole,

at least not on a dynamical time scale, even though its rest mass exceeds the maximum

allowed rest mass of a spherical, nonrotating star by about 45%. There is only a small

amount of shock heating, which rules out thermal pressure as the origin of the extra

support against collapse. As noted, the angular momentum J/M

is smaller than the Kerr

limit and therefore cannot prevent black hole formation. Uniform rotation can increase the

maximum allowed rest mass for  = 2(n = 1) polytropes only by about 20%.

However,

the remnant core is differentially rotating as opposed to uniformly rotating, as shown in

Figure 16.6. The remnant is thus a “hypermassive neutron star” of the type discussed in

Chapter 14.1.2. The formation of hypermassive neutron stars following binary neutron

mergers were foreshadowed by Newtonian simulations;

relativistic equilibrium models

for such stars were then constructed numerically and tested for dynamical stability by

performing simulations in general relativity.

But the calculations of Shibata and Ury

(2000) were the ﬁrst simulations in full general relativity to demonstrate that hypermassive

stars can actually form during binary neutron star mergers.

Both models I2 and I3, for which the total rest mass exceeds the maximum allowed

spherical mass by 63% and 85%, respectively, form a black hole promptly upon merger.

In Figure 16.7 we show snapshots of the density contours and velocity proﬁles for the

more massive model I3. In the last frame the thick solid line denotes the location of an

apparent horizon, indicating the formation of a black hole. By means of these simulations,

Shibata and Ury

u (2000) conclude that hypermassive remnants will form whenever the

rest mass of each star is less than about 70–80% of the maximum allowed mass of the

spherical star, otherwise a black hole will form. As demonstrated by simulations discussed

Cook et al. (1994b); see Table 14.1.

See, e.g., Rasio and Shapiro (1999).

Baumgarte et al. (2000); see Chapter 14.2.

548 Chapter 16 Binary neutron star evolution

0.3c

t = 0.00P

X / M

−5

−10

t = 0.41P

−5

−10

t = 0.81P

X / M

−5

−10

t = 1.41P

t = 1.81P

Y / M Y / M Y / M

Y / MY / MY / M

−5

−10

X / M

−5

−10

t = 1.15P

−5

−10

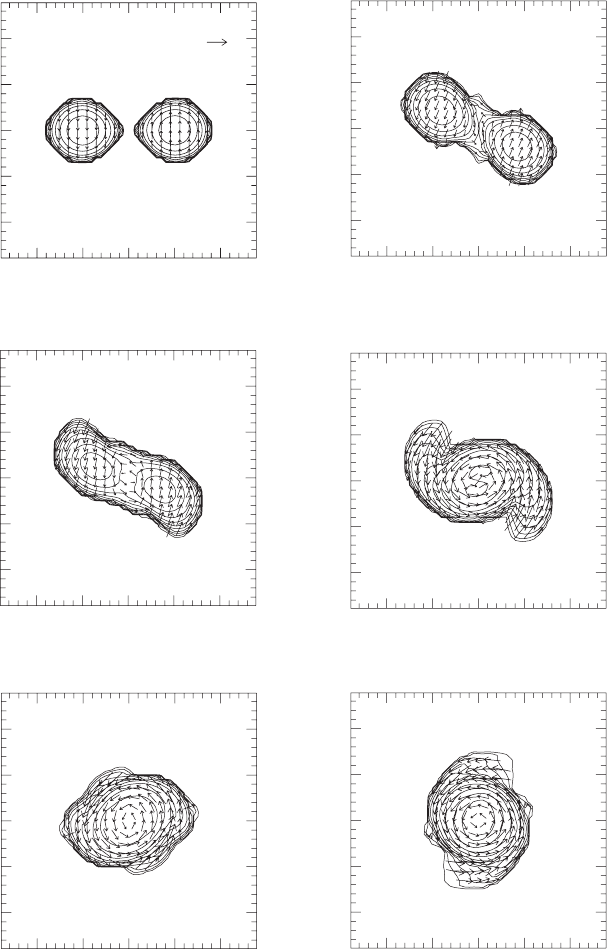
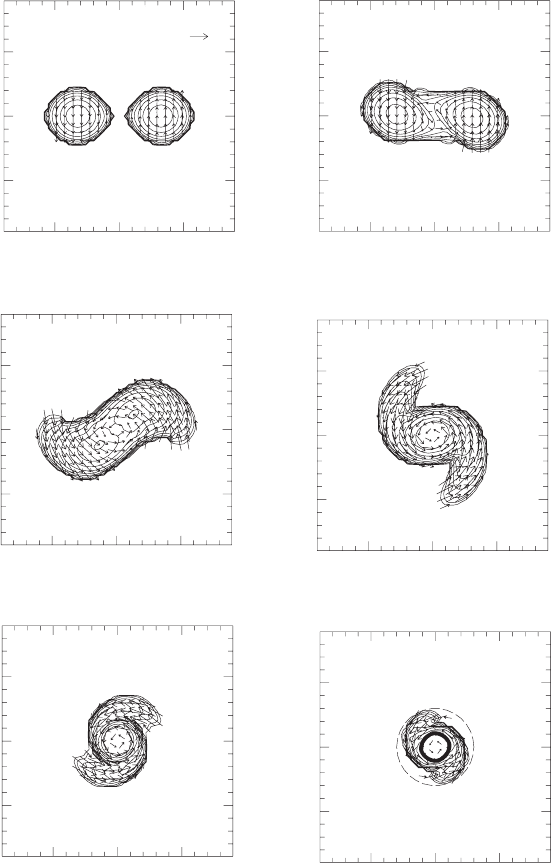
Figure 16.5 Snapshots of density contours for ρ

∗

= γ

1/2

W (see equation 5.12) and the velocity ﬁeld (v

)

in the equatorial plane for the coalescence of an irrotational binary of total rest mass

= 0.261 (Model I1 in

Table 16.1). Time is measured in terms of the initial orbital period P. The contour lines denote densities

∗

/ρ

∗ max

= 10

−0.3 j

with ρ

∗ max

= 0.255 and j = 0, 1, 2,...,10. [From Shibata and Ury

u (2000).]

16.3 Fully relativistic simulations 549

0.2

0.15

0.1

ΩM

0.05

246

X / M, Y / M

81012

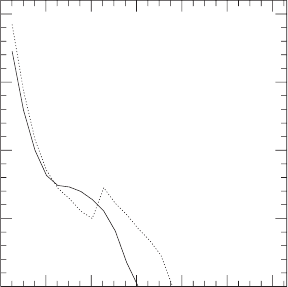
Figure 16.6 The angular velocity  along the x-axis (solid line) and the y-axis (dotted line) at t = 1.81P for

model I1. [From Shibata and Ury

u (2000).]

in Chapter 14.2, hypermassive stars prove to be unstable on secular timescales: dissipative

mechanisms such as shear viscosity or magnetic ﬁelds tend to bring the stars into more

uniform rotation, resulting in a “delayed collapse” to a black hole.

Shibata and Ury

u (2000) ﬁnd fairly similar results for corotational binary models.

Probably the most signiﬁcant difference is that corotational binaries have more angu-

lar momentum prior to merger, which leads to the formation of spiral arms during the

coalescence. The spiral arms contain a few percent of the total mass, and may ulti-

mately form a disk around the central object. For corotational binaries that promptly

form black holes, a disk of mass ∼0.05–0.1M

forms, where M

is the total rest-

mass of the system. For irrotational binaries, the disk mass is much smaller, less

than 0.01M

In these early simulations one of the largest limitations on the accuracy involved is

the outer boundaries. Because of limited computational resources, these boundaries had

to be imposed well within one gravitational radiation wavelength from the binary (at

about λ

/3). This means that the waves were not being extracted in the radiation zone,

which necessarily introduces error unless a special near-zone wave extraction algorithm is

implemented. After gaining access to a more powerful supercomputer, Shibata and Ury

(2002) decided to repeat their calculations on computational grids that extend further,

to about a gravitational wavelength. Their improved calculation, performed on uniform

grids with typical size 505 × 505 × 253, gave results in good qualitative agreement with

their earlier ones, although the onset of black hole formation shifts to slightly smaller

masses. Most strongly affected by this improvement are the gravitational waveforms. In

Figure 16.8, we show examples from these improved simulations for models that are similar

to model I1, leading to a hypermassive neutron star remnant, and model I2, leading to a

black hole. The quantities are plotted for an observer along the z-axis and are deﬁned

550 Chapter 16 Binary neutron star evolution

0.3c

X / M X / M

t = 0.00P

t = 0.46P

Y / M

−5

t = 0.92P

t = 1.36P

t = 1.44P

−5

t = 1.15P

−5

Figure 16.7 Same as Figure 16.5, but for a binary of total rest mass

= 0.332 (Model I3 in

Table 16.1). Contour lines denote densities ρ

∗

/ρ

∗ max

= 10

−0.3 j

with ρ

∗ max

= 0.866 and j = 0, 1, 2,...,10.

The dashed line in the last snapshot is the circle at r = 3M, which encloses over 99% of the total rest mass. The

thick solid line at r/M ≈ 1 denotes the location of the apparent horizon. [From Shibata and Ury

u (2000).]