Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

14.2 Evolution: instabilities and collapse 491

after the start of excision. As a result the mass and spin of the black hole settle down to their

ﬁnal stationary values, an indication that the adoption of the Cowling approximation to

evolve the matter from this time forward is justiﬁed.

The ﬁnal values are consistent with

the earlier estimates of Shibata and Shapiro (2002): the ﬁnal black hole contains about 95%

of the total rest mass of the system and has a spin parameter J

≈ 0.70. This ideal gas

simulation correctly ﬁnds that accretion of rest mass by the black hole eventually becomes

quite small (

∼

−6

in geometrized units

) due to the absence of a dissipative agent

in the disk, like viscosity or magnetic ﬁelds, that can transport the angular momentum of

the orbiting gas outwards. We shall return to this same problem in Section 14.2.5 where

we consider the role of magnetic ﬁelds on the collapse and its aftermath.

An alternative determination of the mass and spin of a black hole, including one sur-

rounded by ﬁelds and matter and possibly still undergoing growth, is provided by the

“isolated-horizon” and “dynamical-horizon” framework discussed in Chapter 7.4.The

approach assumes the existence of an axisymmetric Killing vector ﬁeld residing on a

marginally trapped surface like an apparent horizon. When there is some energy ﬂux across

the horizon, the isolated-horizon formalism must be replaced by the dynamical-horizon

formalism.

Baiotti et al. (2005) have simulated the collapse of rotating, polytropic neu-

tron stars to Kerr black holes to explore this framework and compare it to other measures of

black hole masses and spins. They employ an HRSC general-relativistic code for the hydro-

dynamics, a BSSN-like scheme to integrate the gravitational ﬁeld equations, a black hole

excision algorithm and a dynamical-horizon routine.

The advantage of the dynamical-

horizon approach is that it provides a measurement that can be computed locally, both in

time and space, without having to determine the entire global spacetime. They also point

out a limitation: the horizon itself, and its distortions, must be axisymmetric, although

this is often not a major drawback in practical applications. Comparing different methods

for measuring black hole mass and spin for cases leading to vacuum Kerr formation they

conclude that the dynamical-horizon approach is simple to implement and can produce

estimates that are accurate and more robust than those of other methods.

14.2.4 Viscous evolution

We have discussed the construction of equilibrium models for differentially rotat-

ing, hypermassive stars in Section 14.1.2 and pointed out in Section 14.2.1 how

To adopt the Cowling approximation in a dynamical simulation, it is necessary that the spacetime be manifestly

stationary in the adopted coordinates, so that time derivatives of the ﬁeld variables vanish. The gauge choices of

Liu et al. (2007) meet this criterion.

In geometrized units the rate of rest-mass accretion, [mass/time], with [mass] ≡ M and [time] ≡ GM/c

≡ M,is

dimensionless.

Note that for a given angular momentum J

, equation (7.75) for the dynamical-horizon mass has the same form as

equation (7.3)usedbyLiu et al. (2007) to estimate M

. In the dynamical-horizon formalism, equation (7.74)isused

to compute J

Their dynamical-horizon analysis is performed with the numerical algorithm of Dreyer et al. (2003).

492 Chapter 14 Rotating stars

relativistic simulations in full 3 + 1 demonstrate that models exist that are stable on

dynamical timescales. But viscosity and magnetic ﬁelds tend to drive differentially rotat-

ing objects toward uniform rotation on secular time scales, and such processes can have

important consequences for hypermassive stars formed in nature. Consider, for example,

the formation of a hypermassive neutron star following the inspiral and merger of a binary

neutron star. The removal of the added centrifugal support provided by differential rotation

can lead to the delayed collapse of the remnant to a black hole, accompanied by a delayed

burst of gravitational radiation.

Both magnetic ﬁelds and viscosity alter the structure of

differentially rotating stars on secular timescales, and tracking their lengthy secular evolu-

tion up to and beyond the onset of collapse presents a strenuous challenge for any numerical

hydrodynamics code. Similarly, tracking the secular accretion of viscous or magnetized

gas from a disk onto a central black hole is computationally taxing for a hydrodynamics

code. Fortunately, numerical relativity has matured sufﬁciently that it is now up to the task

in all of these cases. We will summarize in this section some representative simulations of

dynamical spacetimes that treat viscosity in full general relativity; in the next section we

will describe simulations that treat magnetic ﬁelds.

Duez et al. (2004) incorporated shear viscosity in their relativistic 2 + 1 and 3 + 1

Wilson–Van Leer hydrodynamics codes to solve the Navier–Stokes equations in general

relativity for a viscous gas. They used their code to track the secular (viscous) evolution of

differentially rotating stars, including hypermassive stars. They adopted equation (5.65)for

the viscous stress-energy tensor, setting the bulk viscosity ζ to zero and the shear viscosity

η according to η = ν

P,whereν

is a constant parameter that can be varied from one

simulation to the next. This form for the viscosity is sometimes chosen for modeling

turbulence in ﬂuids.

For sufﬁciently small coefﬁcients ν

secular effects will take many

rotation periods to affect the velocity proﬁle and structure of a differentially rotating star

signiﬁcantly. Accordingly, Duez et al. (2004) chose the coefﬁcient large enough to make

a numerical evolution feasible. At the same time, they were careful to keep it sufﬁciently

small to guarantee that the viscous time scale τ

vis

∼R

/ν,whereν ≡ η/ρ

, remains much

longer than the dynamical time scale τ

dyn

≈ (R

/M)

1/2

to mimic the physical behavior of

any realistic ﬂuid. Maintaining such an inequality usually guarantees that for a dynamically

stable conﬁguration, secular evolution proceeds in a quasistationary manner.

Duez et al. (2004) demonstrated that the secular evolution exhibits scaling behavior.

Speciﬁcally, consider the quasistationary evolution of the same star, once with viscous

time scale τ

vis

= τ

and once with τ

vis

= τ

. Provided both τ

and τ

obey the inequality

vis

 τ

dyn

then the conﬁguration of the star with viscosity τ

at time t is the same as the

conﬁguration of the star with viscosity τ

at time (τ

/τ

)t. The results of any one secular

simulation with a given choice of ν

and τ

vis

can then be scaled to any other choice without

having to rerun the simulation.

Baumgarte et al. (2000).

This viscosity law is also used in some accretion disk models; see, e.g., Balbus and Hawley (1998).

14.2 Evolution: instabilities and collapse 493

Fluids with viscosity do not evolve isentropically; viscosity generates heat, as shown by

equation (5.70). The gas may then cool, in principle, via neutrinos in the case of neutron

stars. To survey the possible range of outcomes, Duez et al. treat cooling in two extreme

opposite limits. In the no-cooling limit, which physically corresponds to τ

cool

 τ

vis

all radiative cooling is ignored. In the rapid-cooling limit, where τ

cool

 τ

vis

, the viscous

heating term is removed from the energy equation (5.69) on the assumption that all thermal

energy generated by viscosity is radiated away immediately.

The simulations of hypermassive stars adopt n = 1 equilibrium polytropes for initial

data, using the differential rotation law given by equations (14.9) and (14.10) with

A = 1.

The value of ν

is chosen so that the viscous time scale satisﬁes τ

vis

≈ 3P

rot

∼10τ

dyn

where P

rot

is the initial central rotation period. Even with viscosity of this magnitude, the

stars need to be evolved for 100–200P

rot

to complete their secular evolution and determine

their ﬁnal fate. The reason is that in most cases, viscosity generates a low-density envelope

around the central core. Since the viscosity law has η ∝ P, the viscosity in the low-density

region is small. Hence the effective viscous time scale increases with time and it takes

longer for the stars to reach a ﬁnal state.

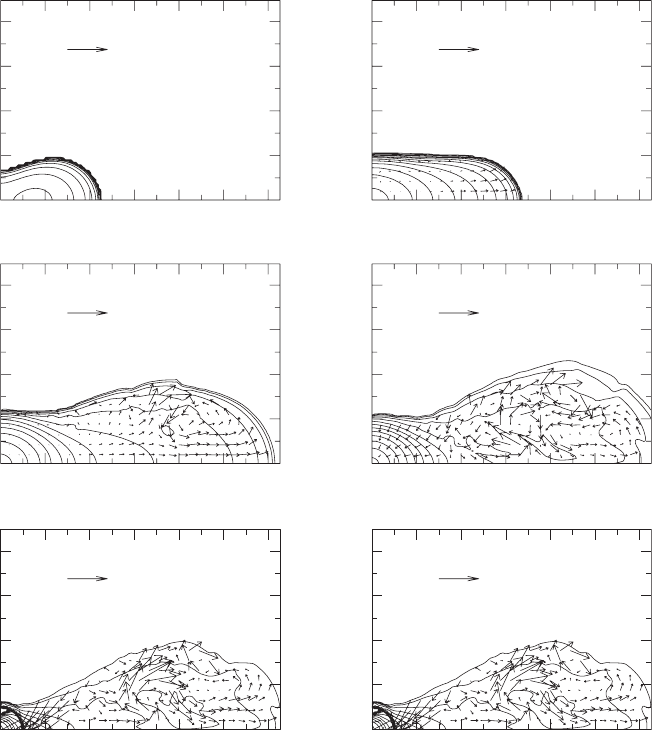
Snapshots during the evolution in axisymmetry of a representative conﬁguration in the

“no-cooling” case are shown in Figure 14.11. Here the initial conﬁguration is a dynamically

stable hypermassive star that is close to the model indicated by the solid dot in Figure 14.1.

It has a mass M

= 1.47M

0,sup

,whereM

0,sup

is the (supramassive) mass limit for uni-

formly rotating n = 1 polytropes (see Table 14.1). The spin parameter is J/M

= 1.0

and the central rotation period is P

rot

= 38M. As the evolution proceeds, viscosity brakes

differential rotation and transfers angular momentum to the outer layers. The core then

contracts and the outer layers expand in a quasistationary manner. As the core becomes

more and more rigidly-rotating, it approaches instability because the star is hypermas-

sive and cannot support a massive rigidly-rotating core. At time t ≈ 27P

rot

≈ 11τ

vis

,the

star becomes dynamically unstable and collapses. An apparent horizon appears at time

t ≈ 28.8P

rot

. Without black hole excision, the code begins to grow inaccurate about 10M

after the horizon appears because of grid stretching. About 30% of rest mass remains

outside the apparent horizon at this point. Using the excision technique described in Sec-

tion 14.2.3, the evolution is extended for another 55M, by which time the system settles

down to a quasistationary, rotating black hole surrounded by a massive, hot ambient disk.

The mass of the black hole at this point is M

≈ 0.82M, while the rest mass and angular

momentum of the ambient disk are M

0,disk

≈ 0.23 M

and J

disk

≈ 0.65J . From conser-

vation of angular momentum the angular momentum of the black hole is inferred to be

≈ 0.35J , giving a spin parameter J

≈ 0.52(J/M

) ≈ 0.52. Viscosity continues

to drive slow, quasisteady accretion of material in the hot disk into the black hole.

The simulations summarized in the plots were performed in axisymmetry, using a

grid of 128 ×128 zones and an outer boundary at 14M. To check the reliability of the

calculation, various diagnostics, like conservation of total mass and angular momentum,

and the constraints, are monitored throughout the simulation. They all seemed to be

494 Chapter 14 Rotating stars

t = 0

t = 4.66 P

rot

t = 18.6 P

rot

t = 28.0 P

rot

t = 28.8 P

rot

0.05c

t = 28.4 P

rot

0.05c

X/M

21012

Z/M

21012

0 2 10 12468

Figure 14.11 Meridional rest-mass density contours and velocity ﬁeld at various times for a hypermassive star

driven to catastrophic collapse by secular (viscous) redistribution of angular momentum. The simulation was

performed by assuming that the system is axisymmetric and experiences no cooling. The levels of the contours

(from inward to outward) are ρ

/ρ

0,max

= 10

−0.15(2 j+0.6)

,where j = 0, 1,...,12. In the lower right panel

(t = 28.8P

rot

), the thick curve denotes the apparent horizon. [From Duez et al. (2004).]

well maintained throughout the simulation.

The circulation C on circular rings on the

equatorial plane is also monitored. In the presence of viscosity, the ﬂow is nonisentropic and

circulation is not conserved, even in the absence of shocks (see equation 5.64). However,

Gravitational radiation carries off some of the mass-energy, but the fractional amount is small. Angular momentum is

automatically conserved in axisymmetry in a conservative code, but not in one based on the Wilson–van Leer scheme.

14.2 Evolution: instabilities and collapse 495

/ 0.2 ) t / P

rot

912

max

(t)/ ρ

ma x

(0)

= 0.4

= 0.2

= 0.1

= 0.05

−4 −3 −2 −10 1

[ t − t

) ] / P

rot

max

(t ) / ρ

max

(0)

= 0.4

= 0.2

= 0.1

= 0.05

Figure 14.12 Scaling behavior exhibited by the evolution of the maximum rest-mass density of a hypermassive

star for different strengths of viscosity, assuming rapid cooling. Upper panel: the curves coincide when plotted

against the scaled time during secular evolution prior to dynamical collapse at t

(ν

). Lower panel: during

dynamical collapse, it is possible to shift the time axes [t → t − t

(ν

)] so that the curves again coincide, which

indicates that viscosity plays an insigniﬁcant role during the dynamical collapse phase. [From Duez et al. (2004).]

the diagnostics show that the simulation properly acounts for the change in circulation due

to viscosity.

In the “rapid-cooling” case, the behavior is qualitatively similar, but since there is no

net viscous heating, the whole process occurs more quickly than in the “no-cooling” case.

The collapse, in particular, now occurs at t ≈ 13.5P

rot

. A plot demonstrating that secular

evolution exhibits scaling with viscosity, while dynamical collapse proceeds independently

of the strength of viscosity, is shown in Figure 14.12. For rapid cooling, the total mass-

energy is not conserved because the thermal energy generated by the viscous heating is

removed, as described above. However, when the mass-energy carried away by thermal

radiation, M

cool

, is accounted for via equation (5.70), the total mass-energy M = M

ADM

cool

is well-conserved.

14.2.5 M HD evolution

In any highly conducting astrophysical plasma, a frozen-in magnetic ﬁeld can be ampliﬁed

appreciably by gas compression or shear (e.g., differential rotation). Even when an initial

seed magnetic ﬁeld is weak, the ﬁeld can grow to inﬂuence the system dynamics signif-

icantly.

Numerical codes have been constructed to treat such situations in relativistic

See, e.g., Shapiro (2000) for a simple, but exact, Newtonian demonstration showing how an arbitrarily small magnetic

seed ﬁeld in a differentially rotating ﬂuid can be ampliﬁed by winding on an Alfv

en time scale to cause the magnetic

braking of all differential motion.

496 Chapter 14 Rotating stars

dynamical spacetimes.

These codes solve the Einstein–Maxwell-MHD system of cou-

pled equations along the lines discussed in Chapter 5.2.4. The two independent codes of

Duez et al. (2005b)andShibata and Sekiguchi (2005) have been used in tandem to tackle

some of the same problems, and the two groups report good agreement. Both of these codes

evolve the spacetime metric using the BSSN formulation and employ an HRSC scheme

to integrate the general relativistic magnetohydrodynamics (GRMHD) equations. Multi-

ple tests have been performed with these codes, including MHD wave propagation and

shocks, magnetized Bondi accretion, MHD waves induced by linear gravitational waves,

and magnetized accretion onto a neutron star.

Hypermassive neutron stars

One of the early applications of the GRMHD codes has been to investigate the evolution of

a hypermassive neutron star (HMNS). As we have already discussed, differentially rotating

stars approach rigid rotation via transport of angular momentum on secular time scales.

HMNSs, however, cannot settle down to rigidly rotating equilibria since their masses

exceed the maximum allowed by uniform rotation. Thus, delayed collapse to a black hole,

and possibly mass loss, can follow transport of angular momentum from the inner to the

outer regions. In the previous section we have described relativistic calculations of HMNS

collapse that have focused on angular momentum transport by viscosity; in Chapter 16

we will describe calculations of angular momentum loss due to gravitational radiation.

Here we focus on simulations of black hole formation triggered by seed magnetic ﬁelds in

HMNSs.

There are at least two distinct effects which amplify the magnetic ﬁeld in a shearing

plasma like an HMNS: magnetic winding and the magnetorotational instability (MRI).

Magnetic winding will occur in a rotating star wherever B

∂

 = 0 and is a simple

consequence of the “frozen-in” condition for a magnetic ﬁeld in MHD. The MRI instability

is a local shearing mode that is triggered wherever ∂

<0, where ! is the cylindrical

radius. When fully developed it will induce turbulence in the gas. Both effects combine

to amplify a magnetic ﬁeld, redistribute angular momentum and brake differential motion.

The MRI poses a challenge for a numerical simulation in that the wavelength of the

fastest-growing MRI mode must be well resolved on the computational grid in order for

the instability to be observed. Since this wavelength is proportional to the magnetic ﬁeld

Duez et al. (2005b); Shibata and Sekiguchi (2005); Ant

on et al. (2006).

For early computations involving GRMHD in dynamical spacetimes, see, e.g., Wilson (1975), who adopts the conformal

ﬂatness approximation to general relativity (see Chapter 16.2), and Sloan and Smarr (1985)andBaumgarte and Shapiro

(2003a,b), who work in full general relativity, and references therein. For computations involving GRMHD in stationary

(e.g., ﬁxed Kerr metric) spacetimes, with emphasis on accretion, see, e.g., Yo k o s a w a (1993); Koide et al. (1999, 2000);

Komissarov (2004); De Villiers and Hawley (2003); Gammie et al. (2003); Anninos et al. (2005) and references

therein.

Shibata et al. (2003b).

Velikhov (1959); Chandrasekhar (1960, 1961); Balbus and Hawley (1991, 1998).

14.2 Evolution: instabilities and collapse 497

strength, it becomes very difﬁcult to resolve for small seed ﬁelds. However, we shall

describe simulations below which succeed in resolving the MRI.

Duez et al. and Shibata used their two independent codes to collaborate on the study

of the effects of magnetic ﬁelds on HMNSs.

In one of their simulations they employed

as initial data essentially the same hypermassive n = 1 polytrope used in the study of vis-

cous evolution described in Section 14.2.4, with a mass of M

= 1.46M

0,sup

and angular

momentum J/M

= 1.0. The matter has the same initial differential rotation proﬁle and is

evolvedasa = 2 ideal gas, as before. Before it is evolved, however, the conﬁguration is

threaded by a weak, purely poloidal magnetic ﬁeld. Cases are then treated in which the max-

imum value of the ratio of the magnetic energy density to gas pressure, C ≡ max(b

/P),

is chosen between 10

−3

and 10

−2

. Such small initial magnetic ﬁelds introduce negligible

violations of the Hamiltonian and momentum constraints, and leave the conﬁgurations in

near dynamical equilibrium. When scaled to an actual HMNS that may arise from a binary

neutron star merger, the value of the adopted initial maximum magnetic ﬁeld strength is

about 10

(2.8M



/M) G. Though numerically small, such a ﬁeld is probably too strong

to model a typical HMNS, but is similar to the ﬁelds believed to form in “magnetars”.

Regardless, it becomes increasingly difﬁcult to evolve ﬁelds that are appreciably smaller,

due to the need to resolve the MRI.

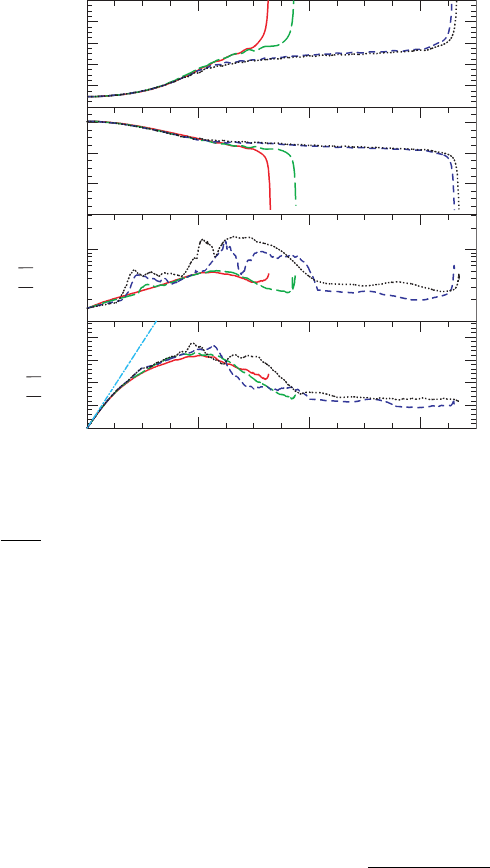
The calculations were performed in axisymmetry on a uniform grid of size (N, N ),

adopting cylindrical coordinates for the MHD. To check the convergence of numerical

results, the simulations were repeated with four different grid resolutions: N = 250, 300,

400 and 500. Figure 14.13 shows the evolution of the central density ρ

, central lapse

, and the maximum values of |B

|(≡|B

|)and|B

|(≡ ! |B

|) as functions of t/P

Here P

≈ 39M = 0.54(M/2.8M



) ms denotes the central rotation period at t = 0. The

central density increases monotonically with time up to the formation of a black hole.

Evolutions with various grid resolutions demonstrate that the results begin to converge

when N

∼

400. On the other hand, results seem far from convergent for N

∼

300. For

example, for low resolutions the maximum values of |B

| prior to saturation are much

smaller than those with higher resolutions, and the growth rate of |B

| is underestimated.

Hence, the effect of MRI, which is responsible for the exponential growth of |B

| on

a dynamical time scale, is not computed accurately for low resolutions. This is because

the wavelength of the fastest growing MRI mode is not well-resolved for low resolutions

(see below).

For the chosen initial seed magnetic ﬁeld, the early evolution is dominated by magnetic

winding of the poloidal ﬁeld, which generates a toroidal ﬁeld B

. When the poloidal seed

ﬁeld is weak and does not inﬂuence the ﬂow, the induction equation (5.140)showsthatB

grows approximately linearly:

(t; !, z) ≈ t! B

(0; !, z)∂

(0; !, z). (14.50)

Duez et al. (2006a,b), Shibata et al. (2006a).

Duncan and Thompson (1992).

498 Chapter 14 Rotating stars

(0)

max

0.6

0.4

0.3

0.2

0.1

0.2

(d)

(c)

(b)

(a)

t/P

−1

−2

max

Figure 14.13 Evolution of the central rest-mass density, central lapse, and maximum values of |B

| and |B

(the behavior of |B

max

is similar to the behavior of |B

max

and is therefore not shown). |B

max

and |B

max

are

plotted in units of

√

max,0

where ρ

max,0

is the maximum rest-mass density at t = 0. The solid, long-dashed,

dashed, and dotted curves denote the results with N = 250, 300, 400, and 500 respectively. The dot-dashed line

in the last panel represents the predicted linear growth of B

at early times. [From Duez et al. (2006a).]

Exercise 14.8 Adopt cylindrical coordinates in axisymmetry to verify equa-

tion (14.50). Assume that the star is rotating with an angular velocity (!, z)

and remains nearly stationary as the ﬁeld ampliﬁes.

Indeed, the early growth rate agrees with the predicted one, as shown in Figure 14.13.

When the energy stored in the toroidal ﬁeld becomes comparable to the energy in differ-

ential rotation, |B

| grows more slowly and the degree of differential rotation is reduced.

Eventually |B

| reaches a maximum and starts to decrease. This should happen on the

Alfv

en time scale t

, where the Alfv

en speed is v



/(ρ

h + b

). For the model

considered here, the minimum value of t

in the star is t

= 15.8P

. So it is not surprising

that the ﬁgure shows the maximum value of |B

| to begin decreasing when t

∼

20P

The MRI is evident at times t

∼

asshowninFigure14.13, where the maximum

value of |B

| suddenly increases rapidly. The wavelength for the fastest growing mode is

MRI

≈ 2πv

/ and the e-folding time of the growth is τ

MRI

= 2

(

∂/∂ ln !

)

−1

For

the adopted initial magnetic ﬁeld strength and rotation proﬁle, this gives λ

MRI

∼R/10

The estimates are based on a local, linear Newtonian analysis as in Balbus and Hawley (1991, 1998).

14.2 Evolution: instabilities and collapse 499

and τ

MRI

∼1P

. The ﬁgure shows the growth of MRI when N

∼

400. For this resolution

the grid spacing is 

∼

MRI

/10, the required scale to study the effect of MRI accurately.

The central density begins to grow more slowly once |B

| saturates, presumably due to

MRI-induced turbulence redistributing some of the angular momentum to slow down the

contraction of the core.

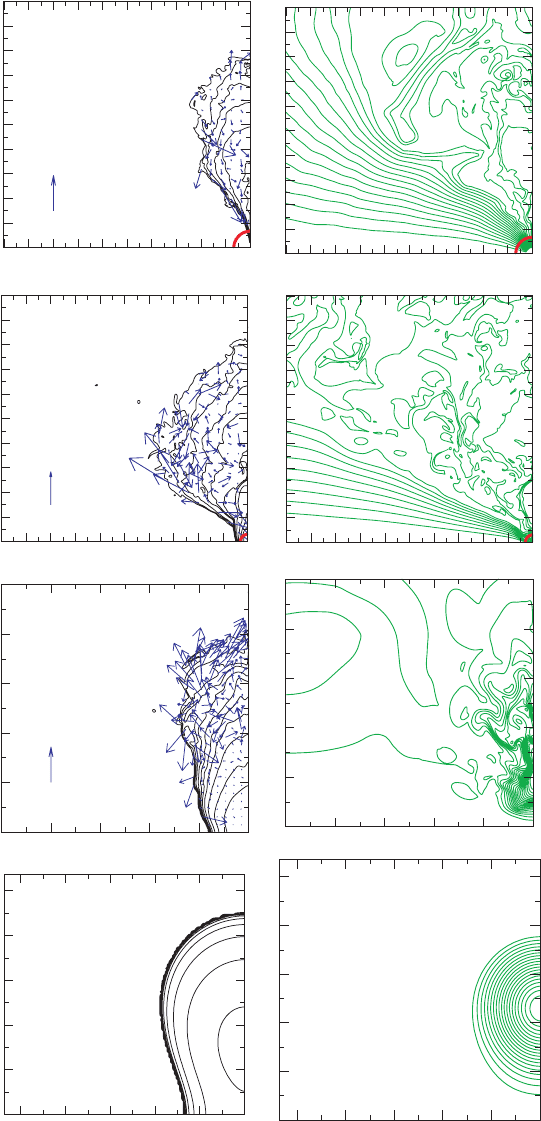
The evolution sequence shown in Figure 14.14 reveals how magnetic braking due to

winding and MRI turbulence combine to trigger gravitational collapse to a black hole. An

apparent horizon forms at t ≈ 66P

≈ 36(M/2.8M



) ms. As we will discuss in Chapter 16,

simulations of binary neutron star mergers show that for a sufﬁciently stiff EOS and typical

observed binary masses, hypermassive star formation is a very possible outcome. Such

remnants become triaxial and strong emitters of gravitational waves in these simulations.

The dissipation time scale of angular momentum due to gravitational radiation is ∼100 ms.

Therefore, a hypermassive remnant with an initially large magnetic ﬁeld (B

∼

G) will

be subject to delayed collapse due to MHD effects (magnetic braking and MRI) rather than

by the emission of gravitational waves. For seed magnetic ﬁelds which are much weaker

than the cases summarized here, gravitational radiation may be the trigger of collapse.

However, it is possible that the MRI may dominate the evolution even in this situation,

since the e-folding time of MRI is independent of the initial ﬁeld strength. A more careful

study of this scenario has to be carried out. However, since any dissipative agent (viscosity,

magnetic ﬁelds, gravitational radiation) serves to redistribute and/or carry off angular

momentum, the ﬁnal fate of a hypermassive star – collapse to a black hole, accompanied

by a gravitational wave burst – is assured.

To follow the evolution after the formation of the apparent horizon, black hole excision

is implemented. The evolution of the irreducible mass of the black hole and the total rest

mass outside the apparent horizon are shown in Figure 14.15.

Soon after formation, the black hole grows rapidly, swallowing the surrounding matter.

However, the accretion rate

gradually decreases and the black hole settles down to a

quasiequilibrium state. At the end of the simulation,

decreases to a steady value of

about 0.01M

. The black hole angular momentum is computed from equations (14.48)

and (14.49), and the mass of the black hole M

is then estimated from equation (7.3). The

estimated value of the black hole spin parameter is then J

∼0.8.

The value of

indicates that the accretion time scale is approximately 10–20P

≈ 5–

10 ms(M/2.8M



). Also, the speciﬁc internal thermal energy in the ambient gaseous

torus near the surface is substantial because of shock heating, indicating that the torus

can be a strong emitter of neutrinos. The ﬁnal system formed after such a delayed col-

lapse of a magnetized HMNS – a rotating black hole + hot accretion torus + collimated

magnetic ﬁeld – has all the attributes proposed for a gamma-ray burst central engine.

Given the timescales and energetics associated with such a delayed collapse, this scenario

was suggested by Duez et al. (2006a) as a particularly good candidate for a short, hard

See, e.g., Piran (1999, 2005); Aloy et al. (2005).

012345

0.05c.

0.1c.

t = 0.0 P

X / M X / M X / M X / M

Z/ M

t = 15.0 P

t = 66.9 P

t = 74.6 P

810

20181614121086420

012 345

Figure 14.14 The upper four panels show snapshots of the rest-mass density contours and velocity vectors on the meridional plane. The lower panels

show the ﬁeld lines (lines of constant A

) for the poloidal magnetic ﬁeld at the same times as the upper panels. The density contours are drawn for

∗

/ρ

∗

max,0

= 10

−0.3i−0.09

(i = 0−12). The ﬁeld lines are drawn for A

= A

φ,min

+ (A

φ,max

− A

φ,min

)i/20 (i = 1−19), where A

φ,max

and A

φ,min

are the maximum

and minimum value of A

respectively at the given time. The thick solid curves in the lower left corners denote the apparent horizon. [From Duez et al. (2006a).]