Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

14.1 Initial data: equilibrium models 471

important role in redistributing the angular momentum and forming a core-halo structure.

It has been shown that, similar to the onset of secular instability, β

can be smaller for stars

with a higher degree of differential rotation.

Until recently, almost nothing has been known about the dynamical bar-mode insta-

bility in relativistic gravitation. The reason was that stable numerical codes capable of

performing reliable hydrodynamic simulations in three spatial dimensions plus time in

full general relativity were not available. In Section 14.2 we shall highlight results from a

few simulations which employ such codes to probe the dynamical stability of relativistic

rotating stars for axisymmetric and nonaxisymmetric modes.

There are numerous evolutionary paths which may lead to the formation of rapidly

rotating, relativistic stars, like neutron stars, with large values of β.

Exercise 14.7 Show that β ∼ 1/R during collapse, assuming conservation of J .

Exercise 14.7 suggests that during supernova collapse, as the core contracts from a

radius of ∼1000 km to ∼10 km, β increases by about two orders of magnitude. Thus, even

moderately rapidly rotating progenitor stars may yield rapidly rotating neutron stars that

may reach the onset of dynamical instability.

These conﬁgurations will be differentially

rotating at birth, even if they were uniformaly rotating prior to collapse, assuming that the

collapse preserves angular momentum on cylindrical shells. Similar arguments hold for

accretion-induced collapse of white dwarfs to neutron stars and for the merger of binary

white dwarfs to neutron stars. In fact, X-ray and radio observations of supernova remnants

have identiﬁed several young, isolated, rapidly rotating pulsars, suggesting that these stars

may have been born with periods of several milliseconds.

These neutron stars could be

the collapsed remnants of rapidly rotating progenitors. By the time they are observed as

pulsars, they are presumably rotating uniformly, given that they are such good clocks.

Rapidly rotating neutron stars naturally arise in the merger of binary neutron stars. As

we will discuss in Chapter 16, simulations reveal that such merger remnants could be

hypermassive neutron stars. Hypermassive stars can also form during core collapse in

massive stars. These conﬁgurations are transient objects that will likely undergo delayed

collapse, producing a delayed burst of gravitational waves and, possibly, gamma-rays.

Their fate may thus be important for the detection and identiﬁcation of gravitational wave

and gamma-ray burst sources.

14.1.3 Collisionless clusters

The ﬁeld equations (14.2)–(14.4) and (G.8) can also be used to construct rotating, axisym-

metric equilibrium conﬁgurations of collisionless matter.

The stress-energy tensor for

the matter in this case is determined by the phase-space distribution function f ,which

Tohline and Hachisu (1990); Pickett et al. (1996); Shibata et al. (2003a).

Rampp et al. (1998).

Marshall et al. (1998); Kaspi et al. (1998).

Shapiro and Teukolsky (1993a,b).

472 Chapter 14 Rotating stars

in turn is governed by the relativistic Vlasov equation.

The stress-energy tensor may be

written in the form



, (14.27)

where p

are the orthonormal components of the particle 4-momentum (see equa-

tions 5.201, 5.213 and 5.215). To solve the ﬁeld equations we need to evaluate the com-

ponents of the stress-energy tensor in the ZAMO frame (see Appendix G). The simplest

phase-space distribution functions that can generate nonspherical, axisymmetric equilibria

are functions solely of the conserved particle energy E and conserved angular momentum

about the symmetry axis. Because E and J

are integrals of the motion, choosing a

distribution function of the form f = f (E, J

) guarantees that we have a solution of the

Vlasov equation, provided the metric is determined self-consistently. No further dynamical

equations need to be solved for the matter. By contrast, for equilibrium ﬂuid systems, such

as rotating stars, we need to integrate the equation of hydrostatic equilibrium, as discussed

above.

For axisymmetric systems described by f = f (E, J

), the quantities E and J

are the two

constants of motion associated with the Killing vectors ξ

(t)

= (∂/∂t)

and ξ

(φ)

= (∂/∂φ)

E ≡−g

(t)

= e

+ ωe

r sin θ p

, (14.28)

≡ g

(φ)

= e

r sin θ p

. (14.29)

In evaluating the integrals (14.27) to obtain the matter source terms appearing in the ﬁeld

equations, we can write

= [( p

)

+ (p

)

+ (p

)

+ m

]

1/2

= [( p

⊥

)

+ (p

)

+ m

]

1/2

, (14.30)

where

⊥

)

= ( p

)

+ (p

)

. (14.31)

The particle momentum distribution is isotropic in a plane containing the symmetry axis,

perpendicular to the φ-direction. In other words,

= p

⊥

cos ψ, p

= p

⊥

sin ψ, (14.32)

and

p = dp

= p

⊥

dψ, (14.33)

and f is now independent of the angle ψ in the symmetry plane. A detailed prescription

for performing the necessary quadratures (14.27) for the source terms can be found in

Shapiro and Teukolsky (1993a,b).

See Chapter 5.3.

14.2 Evolution: instabilities and collapse 473

By suitable choice of the distribution in J

, one can construct models that are either

prolate or oblate. A depletion in the J

-distribution produces a prolate conﬁguration, while

an enhancement produces an oblate one. The easiest way to implement this procedure is

to write

f (E, J

) = g(E)h(J

) (14.34)

and vary h appropriately. When h is constant, we get spherical models with isotropic

velocity distributions. If h depends only on the magnitude of J

, the models are nonspherical

with no net angular momentum. As h is varied, one can build entire sequences of equilibria

with varying degrees of rotation. Bound systems of ﬁnite extent require that g(E) = 0for

E > E

max

,whereE

max

< m

is the maximum particle energy and m

the particle rest mass.

The construction of rotating clusters using this prescription has already been implemented

in Chapter 10.4, where we focused on toroidal clusters and their collapse to black holes.

14.2 Evolution: instabilities and collapse

As suggested above, numerical relativity has proven to be an invaluable tool in probing the

stability of relativistic rotating equilibria, particularly where no theorems exist to identify

unstable conﬁgurations easily or unambiguously. Numerical relativity can also follow the

evolution of unstable conﬁgurations and ascertain their ﬁnal fate. We shall now illustrate

these applications of numerical relativity by summarizing a few representative simulations.

14.2.1 Quasiradial stability and collapse

Uniformly rotating stars with stiff EOSs

Consider the point of onset of quasiradial dynamical stability along a sequence of uniformly

rotating, ﬂuid stars at the mass-shedding limit.

Adopt a polytropic EOS with index n = 1,

 = 2, so as to crudely mimic a stiff nuclear EOS appropriate for a neutron star. Such a

sequence is shown by the solid curve in Figure 14.2, together with a TOV sequence of

nonrotating, spherical stars denoted by the dotted curve for comparison. We are particularly

interested in the supramassive conﬁgurations residing along the solid curve.

The stability theorem of Friedman, Ipser and Sorkin can be applied to show that the onset

of secular instability for these uniformly rotating models resides very close to the central

rest-mass density ρ

0,c

= ρ

crit

at which M assumes its maximum value along the sequence.

According to our discussion in Section 14.1, stars with ρ

0,c

>ρ

crit

are likely candidates for

dynamical instability, but there are no theorems to prove this expectation. The open circles

on the curve identify 5 speciﬁc conﬁgurations chosen as initial data for hydrodynamical

evolution. In some of the simulations, the star is subjected to an initial perturbation by

Shibata et al. (2000a).

See Figure 4 of Cook et al. (1994b).

474 Chapter 14 Rotating stars

0 0.002 0.004

0,c

0.006

1.6

1.4

(A)

(B)

(C)

(D)

(E)

1.2

Figure 14.2 Total mass as a function of central rest-mass density for uniformly rotating polytropes with  = 2

and polytropic parameter K = 200/π. The solid line shows the exact sequence at the mass-shedding limit; the

dashed line gives the TOV sequence of nonrotating, spherical stars. The open circles indicate conﬁgurations at

the mass-shedding limit constructed from the conformal ﬂatness approximation, which were used for the

simulation. The supramassive conﬁgurations chosen as initial data for dynamical evolution calculations are

labeled by (A)–(E). [From Shibata et al. (2000a).]

depleting the initial pressure everywhere a small, ﬁxed, fractional amount below its equilib-

rium value to help induce an instability. In such cases, the Hamiltonian and momentum con-

straint equations are re-solved to restore valid initial data. The response of each star to such

a perturbation then establishes where along the sequence a dynamical instability sets in.

The simulations are performed with a relativistic hydrodynamics code in 3 + 1 dimen-

sions.

The ﬁeld solver is based on second-order ﬁnite-differencing of the BSSN equa-

tions, which were presented in Chapter 11.5. The adiabatic hydrodynamic equations are

integrated by a Wilson scheme as described in Chapter 5.2.1, with the advection terms

differenced by the second-order algorithm of van Leer (1977) and the use of artiﬁcial

viscosity to handle shocks. The adiabatic index during the evolution is chosen to be  = 2,

the same value that relates the pressure and rest-mass density in the equilibrium polytrope.

An “approximate” maximal time slicing condition (K

≈ 0) is employed to determine the

lapse function α and an “approximate” minimum distortion (AMD) spatial gauge condition

(

(∂

˜γ

) ≈ 0) is used to determine the shift vector β

Reﬂection symmetry about the

equator at z = 0andπ− rotation symmetry about the z-axis is assumed. The integrations

are performed on a ﬁxed, uniform grid, typically with 153 × 77 ×77 zones in the x–y–z

See Shibata (1999a) for details. We will discuss applications that employ more advanced codes later in this chapter

and in other chapters.

See Chapter 4; an extra contribution is added to the shift to increase the resolution near the origin when a black hole

forms, as discussed at the end of Chapter 4.5.

14.2 Evolution: instabilities and collapse 475

0.6

0.55

0.5

α(r=0)

0.45

0.4

0.35

(r=0)

0.006

0.005

0.004

0.003

0.002

(A)

(B)

(C)

(D)

(E)

(D)

(C)

(B)

(A)

t / P

0 2 2.5

2 2.50

0.5

1 1.5

Figure 14.3 The central lapse α and rest-mass density ρ

0,c

as functions of time during the evolution of stars

(A)–(E). Here time t is expressed in units of P, the initial rotation period of the star. The solid lines denote the

results without an initial pressure perturbation, while dotted lines show results for a fractional pressure decrease

of 1% everywhere. [From Shibata et al. (2000a).]

directions, respectively. With this grid the semi-major axes of the stars, along the x-andy-

axes, are covered by 40 grid points while the semi-minor (rotation) axis along z is covered

by 23 or 24 grid points.

The main results of the simulation are shown in Figure 14.3, which show the evolution

of ρ

0,c

and α

for each star. When ρ

0,c

<ρ

crit

(i.e., stars A, B and C), the rotating stars

oscillate independently of the initial pressure perturbation. Hence these stars are stable

against gravitational collapse. Small amplitude oscillations at the fundamental quasiradial

period arise for these stars even in the absence of initial pressure perturbations. These

oscillations are caused by small deviations of the initial data from true equilibrium states,

due partly to numerical truncation error and partly to approximations used in solving the

equilibrium equations.

In the absence of a pressure perturbation (P = 0), star D does

not collapse, but it does undergo a much larger amplitude oscillation than those of stars

A–C. More signiﬁcantly, when subjected to a perturbation P/P = 1%, it collapses to a

black hole, unlike stars A–C. The results for star E are similar to, but more pronounced, than

those for star D. By studying these results and reﬁning the initial models and the resolution,

we conclude that the point of onset of dynamical instability along mass-shedding sequences

nearly coincides with the onset of secular instability.

We also learn from these simulations that the unstable stars collapse to rotating black

holes within about one rotation period. The appearance of a black hole is determined by

The conformal ﬂatness approximation for the spatial metric, γ

= e

4φ

, was adopted to construct these models. This

simpliﬁcation typically provides an excellent approximation to exact axisymmetric equilibrium models, as shown by

Cook et al. (1996) and suggested by the proximity of the models in Figure 14.2 to the exact equilibrium curve.

476 Chapter 14 Rotating stars

ﬁnding an apparent horizon. All the rest mass and angular momentum, and almost all

of the total mass-energy (apart from a small amount of gravitational radiation), wind up

in the black holes. The spin parameters J/M

∼0.6 < 1 of all the stars are thus nearly

conserved, and the resulting Kerr black holes have only moderate spin rates. In no case is

there any formation of a massive disk or any ejecta around the newly formed Kerr holes,

even though the progenitors are rapidly rotating. The qualitative reason for this outcome

is clear: because they are slowly spinning, the spacetime outside each of the black holes

is not far from Schwarzschild. The innermost stable circular orbit (ISCO) around each

black hole is roughly r

ISCO

∼5M in our adopted spatial gauge, which is comparable to

isotropic coordinates in a spherical spacetime. However, the stellar equatorial radius R

the equilibrium star is less than 5M, hence at the outset the star already resides inside the

radius which becomes the ISCO of the ﬁnal black hole. This same argument suggests that

the formation of a disk around a black hole requires equilibrium progenitors constructed

either with softer EOSs (higher n) if they are uniformly rotating, or with differential

rotation, so that the initial equatorial radii will be larger. This suspicion is borne out by

other simulations, which we shall summarize below.

During the collapse to a black hole, nonaxisymmetric perturbations do not have enough

time to grow appreciably. But again this is not surprising, given that the progenitor is so

compact, whereby the star can contract by at most a factor of three before a black hole

forms. Hence T/|W |, which approximately scales with R

−1

, can increase only by about a

factor of three over its initial value of (T /|W |)

init

∼0.09, and only barely reach the critical

value of dynamical instability for bar formation, (T /|W |)

dyn

∼0.27. We expect that these

results hold for any uniformly rotating star constructed from a moderately stiff EOS, for

which the corresponding critical conﬁgurations are similarly compact. For progenitors

constructed with softer EOSs, or with differential rotation, the initial radii will be larger

and T /|W | may be ampliﬁed to larger values by the end of collapse. We shall return to the

issue of bar instabilities in Section 14.2.2.

Uniformly rotating n = 3 polytropes

To study the fate of radially unstable, rotating stars constructed from softer EOSs, consider

the adiabatic evolution of an n = 3 polytrope that is marginally unstable to quasiradial

collapse and rotating uniformly at the mass-shedding limit.

Such a conﬁguration can be

used to model a spinning supermassive star, or the stellar core of an evolved, massive Pop-

ulation I star, or even a massive, “ﬁrst generation”, zero-metallicity Population III star, all

at the onset of collapse.

The marginally unstable critical conﬁguration is characterized by

the nondimensional ratios R

/M ≈ 640, R

/M ≈ 420, J/M

≈ 0.97 and T /|W |≈0.97,

Shibata and Shapiro (2002).

Ve ry m as si ve ( M

∼



) and supermassive stars supported by thermal radiation pressure can be modeled by n ≈ 3

polytropes. The cores of young, high-mass Population I stars (M

∼

20M



) are supported by degenerate relativistic

electrons, for which the EOS satisﬁes  = 4/3. These cores can also be modeled by n = 3 polytropes. For an overview

of the astrophysical and cosmological signiﬁcance of this calculation, see Liu et al. (2007), and references therein.

14.2 Evolution: instabilities and collapse 477

independently of its mass,

and is very centrally condensed. Tracking the collapse of such

a conﬁguration is computationally challenging, since the equatorial radius will decrease

by a factor of nearly 10

by the time a black hole forms, requiring a code with considerable

dynamic range. The challenge can be met by (1) restricting the integrations to axisym-

metry

and (2) moving the outer boundary inward at various stages during the collapse

in order to rezone the spatial domain with ﬁner grid spacing (“poor man’s AMR”).

Implementing both of these techniques improves the resolution of the strong-ﬁeld, central

regions where the black hole forms. Because the critical conﬁguration is independent of

M, a single calculation may be scaled to stars of arbitrary mass.

The simulation is carried out with the same basic 3 +1 code used for the previous

problems, but now adapted to axisymmetry. The Einstein ﬁeld equations are solved in

Cartesian coordinates with a grid of size (N, 3, N)in(x, y, z), covering a computational

domain 0 ≤ x, z ≤ L and −y ≤ y ≤ y. Here the grid size N is a constant ( 1), L

the location of the outer boundary, which is moved inwards at discrete moments during the

simulation, and y is the grid spacing in the y-direction, with an axisymmetric boundary

condition imposed at y =±y; the spin axis is along z. This way of “axisymmetrizing”

a3+ 1 Cartesian code is referred to as the “cartoon method” in numerical relativity.

One can solve the relativistic hydrodynamics equations in axisymmetry with the same

“cartoon” recipe. Instead, somewhat improved accuracy is achieved in this simulation

if the equations are recast directly in cylindrical coordinates, using the same Cartesian

variables in the expressions and the same grid points. Maximal time slicing and the AMD

shift condition are adopted as gauge conditions. The appearance and growth of a black

hole is again determined by ﬁnding an apparent horizon.

Violations of the constraints and conservation of mass and angular momentum are mon-

itored as numerical accuracy checks during the simulation. Total angular momentum J and

total baryon rest mass M

should be strictly conserved in axisymmetry. The gravitational

mass M is not conserved, due to the emission of gravitational radiation, but the decrease

in M is very small.

The collapse proceeds homologously early on and results in the appearance of an

apparent horizon at the center at t/M ∼30 630. The ﬁnal black hole contains about 90%

of the total rest mass of the system and has a spin parameter J/M

∼0.75. The remaining

gas forms a rotating disk about the black hole. In fact, these black hole and disk parameters

can be calculated analytically to reasonable approximation from the initial stellar density

and angular momentum distributions

using the fact that in axisymmetry, the speciﬁc

angular momentum spectrum, i.e., the integrated rest mass of all ﬂuid elements with

Baumgarte and Shapiro (1999).

A PN simulation in 3 + 1 dimensions by Saijo et al. (2002) indicates that nonaxisymmetric instabilities are not excited.

This trick is possible because for n ≈ 3andT/|W | small, the collapse proceeds homologously in the central regions

during the early, Newtonian stages; see Shapiro and Teukolsky (1979); Goldreich and Weber (1980); Saijo et al. (2002).

Alcubierre et al. (2001). See Bardeen and Piran (1983); Evans (1986), Ruiz et al. (2008b) for proceedures for

regularizing the ﬁeld equations to deal with the coordinate singularities that arise at the origin or along the axis when

working in spherical symmetry or axisymmetry.

Shapiro and Shibata (2002).

478 Chapter 14 Rotating stars

speciﬁc angular momentum j less than a ﬁducial value, is strictly conserved in the absence

of viscosity.

The fact that a substantial disk forms containing about 10% of the initial

rest mass may have important implications for the “collapsar” model of long-duration

gamma-ray bursts

which posits that the central engines of such sources are rotating black

holes surrounded by gaseous, magnetized disks that arise from the collapse of massive

stars. To be conﬁdent that the evolution has reached stationary equilibrium, it is necessary

to evolve the implosion well past the appearance of an apparent horizon. Accomplishing

this requires the implementation of some technique that avoids the build up of numerical

errors due to the presence of the black hole singularity. In Section 14.2.3 we will discuss

simulations that adopt one such technique, namely “black hole excision”, to repeat and

extend this astrophysically important collapse calculation.

The mass fraction that forms an ambient disk about the rotating black hole is a sensitive

function of the polytropic index of a marginally unstable progenitor star rotating uniformly

at the mass-shedding limit. As the polytropic index decreases below n ≈ 3, the mass

of the disk decreases rapidly. This result has been demonstrated both numerically

and

analytically.

For 2/3 < n < 2, the disk mass fraction is very small (< 10

−3

Differentially rotating hypermassive stars

Consider next the stability of a differentially rotating, hypermassive stars. Adopt the

hypermassive equilibrium conﬁguration marked by the dot in Figure 14.1 as initial data

for the same 3 + 1 code used to evolve the supramassive stars whose radially stability

we studied above. This hypermassive model has

−1

= 1, R

/M ∼5andβ ∼0.23. The

result of the simulation

is summarized in Figure 14.4. Little change is observed in the

density variable ρ

∗

≡ ρ

(−g)

1/2

and velocity proﬁles of the conﬁguration over several

central rotation periods. This simulation thus proves that at least some hypermassive stars

are dynamically stable, both to radial and nonradial modes. But their secular stability is

another issue, to which we will return in Sections 14.2.4 and 14.2.5.

14.2.2 Bar-mode instability

Next consider the dynamical stability of differentially rotating, highly relativistic stars

against bar-mode formation. Numerical simulations to study this instability have been

performed in full 3 + 1 general relativity, again with the same BSSN, relativistic hydro-

dynamics code discussed in the previous section.

Compact, radially stable, equilibrium

stars with M/R

∼

0.1 were constructed as initial data; here M is the total ADM mass and

R the equatorial circumferential radius. A polytropic EOS with n = 1 and a differential

Stark and Piran (1987).

MacFadyen and Woosley (1999); MacFadyen et al. (2001).

Shibata (2004).

Shapiro (2004a).

Baumgarte et al. (2000).

Shibata et al. (2000b).

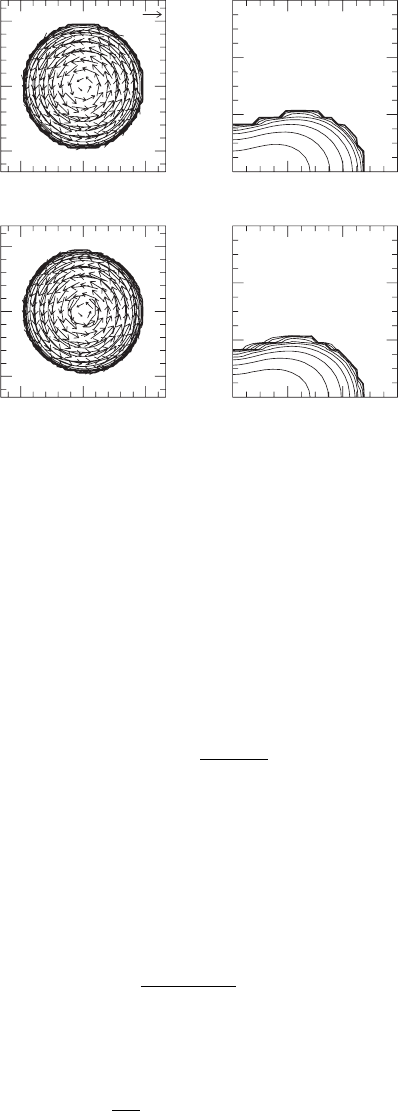
14.2 Evolution: instabilities and collapse 479

0.2c

Y/M

Z/M

X/M

Z/M

t = 0.00P

t = 3.15P

−5

Figure 14.4 Snapshots of contours of the density ρ

∗

of the hypermassive star marked with a dot in Figure 14.1.

We show contours of the initial data and after about 3 central rotation periods, both in the equatorial plane (left,

including the velocity ﬁeld v

= u

), and in a meridional plane containing the z-axis of rotation (right). The

star has a rest-mass about 60% larger than the maximum nonrotating rest mass. The simulation shows that this

model is dynamically stable. [From Baumgarte et al. (2000).]

angular velocity proﬁle speciﬁed by equation (14.11) were employed, and the evolutions

were performed adiabatically with adiabatic index  = 2.

To investigate the dynamical stability against bar-mode deformation, a nonaxisymmetric

density perturbation was imposed of the form

new

= ρ



1 + δ

− y



, (14.35)

where ρ

denotes the original axisymmetric density distribution, and where δ

was chosen

to be 0.1 or 0.3. The 4-velocity components u

were left unperturbed. The constraint

equations were then re-solved to guarantee that, although the perturbed conﬁguration is

no longer in strict hydrostatic equilibrium, the Einstein equations are obeyed at t = 0. The

growth of a bar mode can be followed by monitoring the stellar distortion parameter

η ≡ 2

rms

− y

rms

+ y

rms

, (14.36)

where x

rms

denotes the mean square axial length

rms



)

∗

1/2

. (14.37)

480 Chapter 14 Rotating stars

0.2

0.3

0.25

0.1

max

2.5

J=0

=1, stable

=1, unstable

=0.8, stable

=0.8, unstable

=0.8, marginal

g/cm

b=0.24, A=0.8

∞

- -b=0.245, A=1

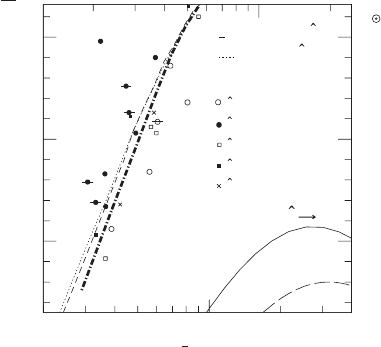
Figure 14.5 Models of differentially rotating stars in a

vs. ¯ρ

∗

max

diagram. Circles denote stars with

A ≡ A/R

= 1, squares with

A = 0.8. Solid (open) circles or squares represent stars that are unstable (stable).

Marginally stable stars are denoted with a cross. The region for the stable stars is clearly separated from that of

the unstable stars by the thick dashed-dotted line. This line is followed fairly closely by the dashed and dotted

lines, which have been constructed for differentially rotating stars of (

A,β) = (1, 0.245) and (0.8, 0.24). The

long-dashed and solid lines in the lower right hand corner are for nonrotating spherical stars and rigidly rotating

stars at the mass-shedding limit. Scales for the top horizontal and right vertical axes are shown for polytropic

constant K = 100(G



), for which the maximum rest-mass for spherical stars is about 1.8M



.[From

Shibata et al. (2000b).]

For dynamically unstable stars, η grows exponentially until reaching a saturation point,

while for stable stars, it remains approximately constant for many rotational periods.

Simulations were performed using a ﬁxed uniform grid with typical size 153 × 77 × 77

in x − y − z and assuming π-rotation symmetry around the z-axis, as well as a reﬂec-

tion symmetry about the equatorial (z = 0) plane. Test simulations with different grid

resolutions were also performed to check that the results do not change signiﬁcantly. By

imposing π-rotation symmetry, one-armed spiral (m = 1) modes are ignored; these may

be dominant for rotating stars in which  is a very steep function of axial radius ! .

The simulations show that when plotted in a

vs. ¯ρ

∗

max

diagram, a region of stable stars

can be clearly distinguished from a region of unstable stars, with the onset of the bar-mode

instability almost independent of the degree of differential rotation (see Figure 14.5).

The simulations also show that the parameter β = T/|W | remains a good diagnostic of

the onset point of instability in the relativistic domain as it did for Newtonian stars. The

critical value for the instability onset depends only weakly on the degree of differential

rotation for the models surveyed. In particular, the critical value of β = β

is ∼0.24 − 0.25,

only slightly smaller than the well-known Newtonian value of about 0.27 for incompressible

Pickett et al. (1996); Centrella et al. (2001); Saijo et al. (2003); Ou and Tohline (2006); Baiotti et al. (2007).