Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

14.1 Initial data: equilibrium models 461

where the metric potentials ρ, γ , ω,andσ are functions of r and θ only. We shall take

the matter source to be described by a stress-energy tensor T

, which, for the moment,

we shall leave unspeciﬁed, to allow for generalization to alternative matter sources.

The

stellar model satisﬁes the Einstein ﬁeld equations G

= 8π T

. These can be arranged to

yield elliptic equations to determine ρ, γ and ω:

∇

[ρe

γ/2

] = S

(r,µ), (14.2)



∇

∂

−

∂



[γ e

γ/2

] = S

(r,µ), (14.3)



∇

∂

−

2µ

∂



[ωe

(γ −2ρ)/2

] = S

(r,µ), (14.4)

where ∇

is the ﬂat-space scalar Laplacian in spherical polar coordinates, µ = cos θ,and

, S

and S

are effective source terms that include the nonlinear ﬁeld and matter terms.

The effective source terms are given in Appendix G. The fourth ﬁeld equation for σ is

slightly more complicated and is also listed in Appendix G.

The three elliptical ﬁeld equations (14.2)–(14.4) can be solved by an integral Green

function approach, as shown by KEH. Among the attractive features of this approach is

that, for large r, the asymptotic ﬂatness conditions ρ ∝ 1/r, γ ∝ 1/r

and ω ∝ 1/r

are

imposed automatically. The integral equations for these functions are given in Appendix G.

Auxiliary relations associated with the matter are discussed below.

14.1.2 Fluid stars

For perfect ﬂuid stars the stress-energy tensor is given by equation (5.4),

= ρ

+ Pg

. (14.5)

The coordinate components of the 4-velocity of the matter can be written as

= u

[1, 0, 0,], u

−(ρ+γ )/2

(1 − v

)

1/2

, (14.6)

where  is the angular velocity of the matter as measured at inﬁnity, and v is the proper

velocity of the matter with respect to a normal observer, often referred to as a “zero angular

momentum observer” or ZAMO

in the literature dealing with rotating equilibria,

v = ( − ω)r sin θ e

−ρ

. (14.7)

Exercise 14.1 Derive equation (14.7).

Hint: Compute γ

≡ (1 − v

)

−1/2

from γ

=−u

Shapiro and Teukolsky (1993a,b).

Bardeen (1973).

462 Chapter 14 Rotating stars

The condition ∇

= 0 yields the equation of hydrostatic equilibrium, which can be

written in differential form as

dP − ρ

h[d ln u

− u

d] = 0. (14.8)

Exercise 14.2 Derive equation (14.8).

The ﬁnal relation required to specify an equilibrium conﬁguration is the rotation law.

For barotropic equations of state where P and h depend only on ρ

, the integrability

condition on equation (14.8) requires either that the rotation be uniform, with d = 0, or

that

= F() (14.9)

for some function F of . In the latter case the conﬁguration is characterized by differential

rotation. A simple choice adopted by KEH is

F() = A

(

− ), (14.10)

where 

is the angular velocity at the center of the conﬁguration and A is a positive

constant with dimensions of length. Combining equations (14.9) and (14.10) yields

(

− ) =

( − ω)r

sin

θe

2(β−ν)

1 − ( − ω)

sin

θe

2(β−ν)

, (14.11)

where, following convention, we have introduced

ν ≡

γ + ρ

and β ≡

γ − ρ

. (14.12)

Equation (14.11) shows that the angular velocity on the rotation axis (θ = 0) is equal to



.AsA →∞,wehave → 

, hence for large A the rotation law approaches rigid

rotation. Exercise 14.3 further illustrates how A parameterizes the characteristic length

scale over which  changes.

Exercise 14.3 Show that in the Newtonian limit, rotation law (14.11) reduces to

/

= 1/



1 + !



, (14.13)

where ! = rsin θ is the usual cylindrical radial coordinate.

Using the thermodynamic relation dh = dP/ρ

together with equation (14.9), allows

us to integrate the equation of hydrostatic evolution (14.8) to obtain

=−



dF() + constant. (14.14)

Adopting the rotation law (14.11)thengives

( − 

)

+ constant. (14.15)

14.1 Initial data: equilibrium models 463

For a polytropic equation of state (EOS) P = Kρ

(1+1/n)

, as in equation (1.86),

equa-

tions (14.6) and (14.15) yield

ln[1 + (1 + n)Kρ

1/n

] +

ln(1 − v

) + ν −

( − 

)

= constant. (14.16)

Note that when using a polytropic EOS, it is always possible to scale out the constant K .

We already noted this in Chapter 1.3 (see equation 1.87), but here we extend the analysis

to nonspherical, rotating polytropes. In gravitational units K

n/2

has units of length, which

leads to the following set of nondimensional quantities, denoted by a bar:

r ≡ K

−n/2

t ≡ K

−n/2

t, ¯ω ≡ K

n/2

ω,

 ≡ K

n/2

,

¯ρ

≡ K

P ≡ K

M ≡ K

−n/2

J ≡ K

−n

J, (14.17)

and so forth. One can thus set K = 1 in numerical integrations and either use the above

relations to scale the results to more physical values of K , or express answers in terms of

nondimensional ratios (e.g., R/M, M

, M, J/M

,etc.).

The iterative algorithm of KEH to solve the coupled equations involves a further rescal-

ing with respect to the equatorial radius

= K

−n/2

. This rescaling simpliﬁes the numer-

ical implementation, since the unknown location of the stellar surface in the equatorial

direction can now be set to unity. We can then parametrize the stellar rotation rate by

setting the polar radius

to a value equal or less than unity: for

= 1thestaris

spherical and nonrotating, and decreasing this ratio (for oblate conﬁgurations) will increase

the angular velocity

. Once all quantities have been expressed in terms of

, this quan-

tity appears as an eigenvalue in equation (14.16), together with 

and the constant on

the right-hand side. A self-consistent solution of Einstein’s ﬁeld equations coupled to the

matter equation (14.16) then involves determining these three eigenvalues. This can be

accomplished by evaluating equation (14.16), given a “guess” for the gravitational ﬁelds,

at three different locations in the star, namely at the pole, on the equator, and at the stellar

center, and then iterating until convergence. We will describe a similar algorithm for the

construction of binary neutron star initial data in more detail in Chapter 15.2.

Diagnostics

Once the coupled system of equilibrium equations is solved self-consistently, a useful set

of physical diagnostics can be computed for each conﬁguration. For equilibrium conﬁg-

urations, the ADM mass must be equal to the Komar mass (see Chapter 3.5). We may

therefore deﬁne the total mass-energy M = M

ADM

of these spacetimes as

M = M

=−



(2T

− δ

)ξ

(t)





(−2T

+ T

)

√

γαd

x (14.18)

Note that KEH adopt a different deﬁnition of a polytropic EOS: P = Kρ

∗(1+1/n)

,whereρ

∗

= ρ

(1 +). Other authors

(e.g., Cook et al. 1992, 1994a,b), use equation (5.18). As a result, equation (14.16) is modiﬁed for KEH.

See exercises 14.4, 14.5 and 14.6 for examples.

464 Chapter 14 Rotating stars

(see exercise 3.31). Here d



is deﬁned below equation (3.124), and ξ

(t)

is the time Killing

vector. The total rest-mass M

isgivenbyequation(3.127),







√

γαu

x. (14.19)

The total proper mass of the system M

is deﬁned as the rest-mass energy M

plus internal

energy U of the star, i.e., the total energy stored in the conﬁguration excluding gravitational

potential and rotational energy,

= M

+ U, (14.20)

where

U =



u







√

γαu

x. (14.21)

The total angular momentum of the system J is given by

J =



(φ)





√

γαd

x, (14.22)

where ξ

(φ)

is the angular Killing vector (see exercise 3.31). The total rotational kinetic

energy of the system T is deﬁned by

T =



dJ =



T

√

γαd

x. (14.23)

Finally, we can compute the gravitational potential energy of the star W as

W = M − M

− T. (14.24)

All of the above integral diagnostics are gauge invariant quantities that reduce to their

Newtonian counterparts in the weak-ﬁeld limit.

Maximum masses, spins and stability

Numerical models of rotating stars obtained by solving the equilibrium equations have been

constructed by many authors.

Equilibrium sequences constructed for a given barotropic

EOS, along which either the rest mass or angular momentum is held constant, are particu-

larly useful. Constant rest-mass sequences often can be used to represent quasistationary

evolutionary sequences, along which some parameter, like the angular velocity, varies

slowly, on a secular time scale. Along a uniformly rotating, equilibrium sequence of

constant M

, changes in M and J are related by

dM = dJ. (14.25)

See, e.g., footnote 7 for detailed model calculations in general relativity. For overviews and additional references

concerning rotating equilibria and stability, see, e.g., Tassoul (1978) for Newtonian conﬁgurations and Shapiro and

Teukolsky (1983) and Stergioulas (2003) for post-Newtonian and general relativistic conﬁgurations.

See Ostriker and Gunn (1969) for a proof in the Newtonian case and Hartle (1970) for the relativistic case.

14.1 Initial data: equilibrium models 465

This relation provides a useful check on the numerical construction of such a sequence.

Equilibrium sequences of constant J are required in order to apply the turning-point

criterion of Friedman, Ipser and Sorkin

to test for quasiradial stability of a uniformly

rotating conﬁguration. This criterion states that along uniformly rotating sequences of

constant J , members of which can be parametrized by their central mass-energy density

∗

= ρ

(1 + 

), those conﬁgurations for which ∂ M/∂ρ

∗

> 0 are secularly stable against

quasiradial perturbations, while those for which ∂ M/∂ρ

∗

< 0 are secularly unstable. The

turning point criterion applied along such sequences can only identify the point of secular,

but not dynamical, instability, since one is comparing neighboring, uniformly rotating

conﬁgurations with the same angular momentum. Maintaining uniform rotation during

perturbations tacitly assumes high viscosity, which acts on a secular time scale. In a

dynamical perturbation, the star will preserve circulation, as well as angular momentum,

but not uniform rotation. While a secular instability evolves on a dissipative (e.g., viscous)

time scale, a dynamical instability evolves on a collapse (free-fall) time scale, τ

∼1/

√

∗

which is much shorter. It is thus possible that a secularly unstable star may be dynamically

stable: for sufﬁciently small viscosity, the perturbed star may change to a differentially

rotating, dynamically stable conﬁguration. Ultimately, the presence of viscosity may bring

the star back into rigid rotation, driving the star to an unstable state. Friedman, Ipser

and Sorkin showed that along a sequence of uniformly rotating stars, a secular instability

always occurs before a dynamical instability, implying that all secularly stable stars are

also dynamically stable.

For spherical star sequences, the points of onset of secular and dynamical instability

coincide, since for a nonrotating star a radial perturbation conserves both circulation

and uniform rotation, and is located at the turning point on the M vs. ρ

∗

equilibrium

curve. This result suggests that for uniformly rotating stars for which the rotational kinetic

energy T is typically a small fraction of the gravitational binding energy |W |, the onset of

dynamical instability is close to the onset of secular instability. Establishing the actual point

of onset of dynamical instability for rotating stars is more complicated. Formalisms have

been developed

to identify points of dynamical instability to axisymmetric perturbations

along sequences of rotating stars. In such formalisms, however, a complicated functional

for a set of trial functions has to be evaluated. Probably because of the complexity of

this method, explicit calculations have never been performed. In practice, to identify the

point of onset of a dynamical instability along an equilibrium sequence of uniformly or

differentially rotating stars, and then to track the resulting evolution and determine the ﬁnal

fate of an unstable conﬁguration, a full numerical simulation employing the equilibrium

model as initial data is required. That is the role of numerical relativity (see Section 14.2).

Nonrotating polytropes with n = 3or = 1 + 1/n = 4/3 are marginally stable to radial

perturbations in Newtonian gravitation, but dynamically unstable in general relativity. The

Friedman et al. (1988).

Chandrasekhar and Friedman (1972a,b,c); Schutz (1972).

466 Chapter 14 Rotating stars

critical  for radial stability for nonrotating stars is raised above 4/3 in general relativity,



crit

= 4/3 + 1.125(M/R). Stars with >

crit

are stable, while those with <

crit

are unstable. Post-Newtonian analysis shows that unstable stars with  near 4/3 can be

stabilized by rotation, which lowers the critical value of . Alternatively, there is a critical

compaction (M/R)

crit

below which a rotating star with n = 3 is radially stable and above

which it is unstable. The critical compaction depends on T/|W |, the ratio of rotational

kinetic to gravitational binding energy. Determining the critical compaction for uniformly

rotating stars with n ≈ 3 requires an analysis correct to second post-Newtonian order.

Uniformly rotating stars at the mass-shedding limit (deﬁned below) with n near 3 are useful

to model rapidly rotating conﬁgurations supported either by the pressure of relativistic

degenerate fermions (e.g., massive white dwarfs or cores of massive, evolved stars) or by

thermal radiation pressure (e.g., very massive and supermassive stars).

The maximum mass of a relativistic star, like a neutron star, is of great astrophysical

interest. Conﬁgurations exceeding the maximum mass limit are likely to collapse to form

black holes. For spherical (static) stars constructed from the same barotropic EOS, the

maximum mass is located at the turning point along the M vs. ρ

∗

equilibrium curve and is

thus marginally stable to quasiradial perturbations. Rotation can support stars with higher

mass than the maximum static limit. Thus, uniform rotation can support these supramassive

stars, but Cook et al. (1992, 1994a,b, hereafter CST) show that supramassive stars have

masses which are typically at most

∼

20% larger than the static limit for the same EOS.

In Table 14.1 we compare maximum mass models for nonrotating and uniformly rotating

polytropes.

Beyond a critical spin rate, the gravitational attraction is insufﬁcient to keep

matter in uniform rotation from ﬂying off the surface. At the so-called mass-shedding

limit, matter at the equator has no outward support from pressure but is instead supported

exclusively by centrifugal forces and therefore follows a circular geodesic. CST ﬁnd that for

a given EOS, the maximum  conﬁguration (i.e., the conﬁguration at the mass-shedding

limit) does not coincide exactly with the maximum mass model, although they are quite

close numerically.

Exercise 14.4 Consider modeling the EOS of a neutron star by a degenerate,

nonrelativistic, neutron gas. Such a gas is described by a polytropic EOS with

n = 3/2and

K =

2/3

4/3

8/3

, (14.26)

where m

is the neutron rest-mass.

Chandrasekhar (1964a,b); Feynmann, unpublished, as quoted in Fowler (1964).

Zeldovich and Novikov (1971); Baumgarte and Shapiro (1999).

See Baumgarte and Shapiro (1999); Shibata (2004) for numerical models.

See, e.g., Cook et al. (1994a) for uniformly rotating models, including maximum-mass models, constructed for 14

realistic nuclear matter EOSs.

See Shapiro and Teukolsky (1983), Section 2.3, for a derivation.

Table 14.1 Maximum mass models for nonrotating and uniformly rotating polytropes. For all stars we list the the polytropic index n,

the total mass-energy

M, the rest-mass

and the central energy density ¯ρ

∗

. For nonrotating stars we also list the areal radius

while for rotating stars we give the equatorial areal radius

, the eccentricity e, the angular velocity measured at inﬁnity

, the total

angular momentum

J and the ratio of the rotational kinetic energy to the gravitational binding energy, T /|W |. All quantities are

expressed in nondimensional units as deﬁned in equation (14.17) (with G = c = 1). Here the notation 5.80(−3), for example, means

5.80 × 10

−3

. [After Cook et al. (1994a).]

Nonrotating Rotating

R ¯ρ

∗

e ¯ρ

∗



JT/|W |

0.5 0.125 0.151 0.395 1.29 0.153 0.182 0.536 0.784 1.04 0.976 0.0172 0.147

1.0 0.164 0.180 0.763 0.420 0.188 0.207 1.09 0.773 0.345 0.378 0.0202 0.0835

1.5 0.264 0.276 1.97 0.0718 0.290 0.304 2.88 0.760 0.0610 0.110 0.0387 0.0475

2.0 0.515 0.523 6.94 5.80(−3) 0.549 0.558 10.3 0.752 5.05(−3) 0.0224 0.120 0.0273

2.5 1.24 1.25 41.0 1.26(−4) 1.29 1.30 61.3 0.749 1.13(−4) 2.37(−3) 0.684 0.0157

2.9 3.23 3.23 620 1.54(−7) 3.32 3.32 947 0.749 1.38(−7) 6.36(−5) 7.82 0.0101

468 Chapter 14 Rotating stars

(a) Show that, in geometrized units, K = 7.327 km

4/3

. Note that K

n/2

has units

of length, consistent with the scaling relations (14.17).

(b) Consult Table 14.1 anduseequation(14.17) to ﬁnd the maximum mass of

nonrotating and uniformly rotating stars governed by this EOS. Given that many

neutron stars are observed to have a mass close to 1.4M



, is this EOS realistic?

Exercise 14.5 The polytropic index n parametrizes the stiffness of the polytropic

EOS. Smaller values of n (and hence larger values of  = 1 + 1/n) describe stiffer

EOSs, while larger values of n (smaller ) describe softer EOSs. Stars governed

by soft EOS are centrally condensed, i.e., most of the star’s mass is concentrated in

a small, high-density core surrounded by an extended, low-density envelope. Stiff

EOSs, on the other hand, lead to stars that have a more uniform density proﬁle.

(a) Compute the compaction M/R for the nonrotating maximum mass models

listed in Table 14.1. Use your results to justify using a stiff polytropic EOS with

n  1 to model typical neutron stars with masses M ≈ 1.4M



and radii R ≈ 15 km.

(b) Compute the fractional difference between M and M

for the nonrotating

models of Table 14.1. Explain its dependence on n in terms of the results for M/R

in part (a).

between the nonrotating

and uniformly rotating maximum mass models listed in Table 14.1. Explain its

dependence on n in terms of the central concentration of these stars.

Exercise 14.6 PSR J1748−2446ad, with a spin frequency of f = 716 Hz, is the

most rapidly spinning pulsar known to date.

(a) Assume that the mass of this pulsar is at least 1.4M



to ﬁnd a lower limit on

the dimensionless product M for this pulsar.

(b) Now survey Table 14.1, assuming that the angular velocities  of the maximum

mass models listed there are very close to the maximum spin models, to ﬁnd which

values of n can support a star like PSR J1748−2446ad.

By contrast with uniform rotation, differential rotation, can support hypermassive stars,

i.e., equilibrium stars which exceed both the nonrotating static and uniformly rotating

supramassive star mass limits. As an example, consider the rotation law given by equa-

tion (14.10) with

A ≡ A/R

,whereR

is the equatorial coordinate radius, and apply it to

an n = 1 polytrope.

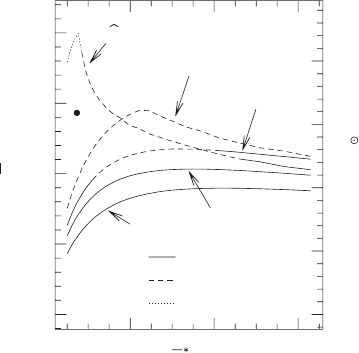
Figure 14.1 shows the maximum M

vs. ρ

∗

relation along sequences

of constant

A. It is clear from the ﬁgure that even modest differential rotation can sup-

port equilibrium stars with masses

∼

50% larger than the static and supramassive limits.

Hypermassive neutron stars can be formed in nature, by, e.g., merging binary neutron stars

or by stellar core collapse followed by accretion fall-back.

Exact criteria do not exist for determining the quasiradial stability of differentially

rotating conﬁgurations, either to dynamical or secular perturbations. Such stability must be

determined by numerical simulations. In Section 14.2 we discuss such simulations, which

See Hessels et al. (2006).

Baumgarte et al. (2000).

For most other polytropic indices, as well as for realistic nuclear EOSs, the increases in maximum mass are typically

somewhat smaller; see Lyford et al. (2003); Morrison et al. (2004).

14.1 Initial data: equilibrium models 469

0.5

0.7

−1

=1.0

0.14<b<0.27

TOV

b<0.14

b>0.27

max

0.2 0.4 0.6

0.4

0.3

0.2

0.1

Figure 14.1 Maximum rest-mass conﬁgurations vs. maximum mass-energy density for differentially rotating

n = 1 sequences of constant

−1

.Valuesofβ = T/|W | for the models are indicated. The mass–density curve

for static TOV equilibrium stars is shown for comparison. The supramassive limit for uniformaly rotating stars

corresponds to the curve

−1

= 0. Masses are given in nondimensional units on the left-hand side (K = 1) and

in solar masses on the right-hand side; the later are calculated by assigning the maximum rest mass for

nonrotating stars to 2M



. The dot marks one particular hypermassive conﬁguration whose stability properties we

will study below. [From Baumgarte et al. (2000).]

reveal, for example, that the hypermassive conﬁguration marked by a dot in Figure 14.1

is dynamically stable. On the other hand, the presence of viscosity or magnetic ﬁelds will

redistribute the angular momentum in a differentially rotating star on a secular time scale,

presumably driving its core toward uniform rotation while depositing the excess angular

momentum in the outermost layers. But uniform rotation alone cannot support such a

core in equilibrium, if it is sufﬁciently massive. As a result, most, if not all, hypermassive

stars are transient objects: conﬁgurations that are dynamically stable initially will evolve

on a secular time scale and may ultimately undergo catastrophic collapse. Relativistic

simulations that demonstrate this behavior are described in Section 14.2.

In addition to quasiradial instabilities, rotating stars are also subject to nonaxisymmetric

instabilities. An exact treatment of these instabilities exists only for incompressible equilib-

rium ﬂuids in Newtonian gravity.

For these conﬁgurations, global rotational instabilities

arise from nonradial toroidal modes e

imϕ

(m =±1, ±2,...) when β ≡ T /|W | exceeds a

certain critical value. Here ϕ is the azimuthal coordinate. In the following we will focus on

the m =±2 bar mode, since it is the fastest growing mode when the rotation is sufﬁciently

rapid.

See, e.g., Chandrasekhar (1969); Tassoul (1978); Shapiro and Teukolsky (1983).

For a discussion of the r -mode instability, which may be important for slowly rotating neutron stars, see Stergioulas

(2003) for review and references.

470 Chapter 14 Rotating stars

There exists two different mechanisms and corresponding timescales for bar-mode

instabilities. Uniformly rotating, incompressible stars in Newtonian theory are secularly

unstable to bar-mode formation when β ≥ β

≥ 0.1375. However, this instability can only

grow in the presence of some dissipative mechanism, like viscosity or gravitational radia-

tion reaction, and the growth time is determined by the dissipation time scale. Interestingly,

for either viscosity or gravitational radiation, the point of onset of the bar-mode instability

coincides for Newtonian stars. By contrast, a dynamical instability to bar-mode formation

requires large spin rates and sets in when β ≥ β

≥ 0.2738. This instability is independent

of any dissipation mechanism, and the growth time is determined by the hydrodynamical

(collapse) time scale of the system.

In the case of compressible Newtonian stars, the secular bar-mode instability for both

uniform and differential rotation has been analyzed numerically within linear perturbation

theory by means of a variational principle and trial functions, and by other approximate

means.

For uniformly rotating polytropes the m = 2 bar-mode instability is again found

to set in at β

 0.14.

However, this mode is reached only when the polytropic index of the

star satisﬁes n ≤ 0.808.

Stars with larger n (i.e., soft EOSs) are too centrally condensed

to support high enough spin in uniform rotation without undergoing mass-shedding at the

equator. This constraint does not apply to differentially rotating stars, which can support

signiﬁcantly more rotational energy in equilibrium, even when the degree of differential

rotation is only moderate. The critical value for the onset of the secular m = 2 bar mode in

Newtonian theory is again β

 0.14 for a wide range of angular momentum distributions

and barotropic equations of state

although for very strongly differentially rotating stars

the critical value can be as small as β

< 0.1.

Similar approximate formalisms have also been applied to analyze the secular bar-mode

instability in post-Newtonian theory

and in full general relativity.

For relativistic stars,

the critical value of β

depends on the compaction M/R of the star, the rotation law and

the dissipative mechanism. The gravitational-radiation driven instability sets in for smaller

rotation rates than in Newtonian theory, i.e., it is triggered for values of β

< 0.14 as the

compaction increases. By contrast, viscosity drives the instability to higher rotation rates

> 0.14 as the conﬁgurations become more compact.

Determining the onset of the dynamical bar-mode instability, as well as the subse-

quent evolution of an unstable star, generally requires a numerical simulation. Simulations

performed in Newtonian theory

have shown that β

depends only very weakly on the

stiffness of the EOS. Once a bar has developed, the formation of spiral arms plays an

Lynden-Bell and Ostriker (1967); Ostriker and Bodenheimer (1973); Friedman and Schutz (1975); Bardeen et al.

(1977); Friedman and Schutz (1978a,b); Ipser and Lindblom (1989).

See, e.g., Managan (1985); Imamura et al. (1985); Ipser and Lindblom (1990, 1991); Lai et al. (1993a).

James (1964).

See, e.g., Ostriker and Bodenheimer (1973); Bardeen et al. (1977); Tassoul (1978).

Imamura et al. (1995).

Cutler and Lindblom (1992); Shapiro and Zane (1998).

Bonazzola et al. (1996); Stergioulas and Friedman (1998).

See, e.g., Tohline et al. (1985); Smith et al. (1996); Pickett et al. (1996); New et al. (2000) and references therein.