Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

14.2 Evolution: instabilities and collapse 481

Maclaurin spheroids. The critical value β

decreases slightly for stars with a higher degree

of differential rotation. When combined with other simulations that adopt the ﬁrst post-

Newtonian approximation of general relativity but are otherwise identical,

one ﬁnds that

decreases with increasing compaction as well. Thus relativistic gravitation enhances

the dynamical bar-mode instability, i.e., the onset of the instability sets in for somewhat

smaller values of β in relativistic gravitation than in Newtonian gravitation. To check the

reliability of these simulations, the conservation of the relativistic circulation, deﬁned by

equation (5.59), was monitored, in addition to rest mass, total mass-energy, linear and

angular momentum. Conservation of circulation indicates that the simulations are not

seriously affected by any spurious numerical viscosity.

For selected models, the growth and saturation of bar-mode perturbations were followed

up to late times. Stars with sufﬁciently large β>β

develop bars ﬁrst and then form spiral

arms, leading to some mass ejection; see Figure 14.6.

Stars with smaller values of β ∼β

also develop bars, but do not form spiral arms

and eject only very little mass. In both cases, unstable stars appear to form differentially

rotating, triaxial ellipsoids once the bar-mode perturbation saturates; see Figure 14.7.

Typically, these ﬂattened ellipsoids appear to have β

∼

0.2, so that they are secularly

unstable to gravitational waves and viscosity. We expect that this secular instability will

allow the stars to maintain a bar-like shape for many dynamical time scales, leading to

quasiperiodic emission of gravitational waves. These expectations are borne out by simula-

tions of merging binary neutron stars, which in some cases result in bar-like, hypermassive

remnants that emit quasiperiodic gravitational waves prior to undergoing delayed collapse

to black holes. We will return to this issue in Chapter 16.

As mentioned, relaxing the constraint of π -rotation symmetry can weaken the m = 2

mode via nonlinear coupling to the m = 1 mode. This effect was studied by Baiotti et al.

(2007)witha3+ 1 general relativistic hydrodynamics HRSC code with a BSSN-like ﬁeld

solver. They found that such an effect can limit the persistence of bar-formation, and in

some cases can even suppress the instability, when β ∼β

, but has little inﬂuence when

β  β

. They also found, not surprisingly, that the nature of the initial perturbation had

little effect on the growth time of the bar-mode instability, but could inﬂuence its duration

when mode mixing is allowed.

14.2.3 Black hole excision and stellar collapse

The formation of a black hole during stellar collapse poses a serious challenge: the black

hole singularity must be avoided to allow the exterior evolution to continue far into the

future. In Chapter 13.1 we discussed several strategies for dealing with this issue in the

context of binary black hole simulations in vacuum spacetimes. Here we will focus on one

of the techniques, black hole excision, which has also proven very successfull in stellar

collapse simulations.

Saijo et al. (2001).

482 Chapter 14 Rotating stars

0510

0.3c

0.1c

0.3c

t=0.00P

t=3.37P

t=5.82P

X / M X / M

0.3c

Y / M

Z / M

−10

−10 −5

0510

−10 −5

−5

−10

−5

0510

−10 −5

−10

−5

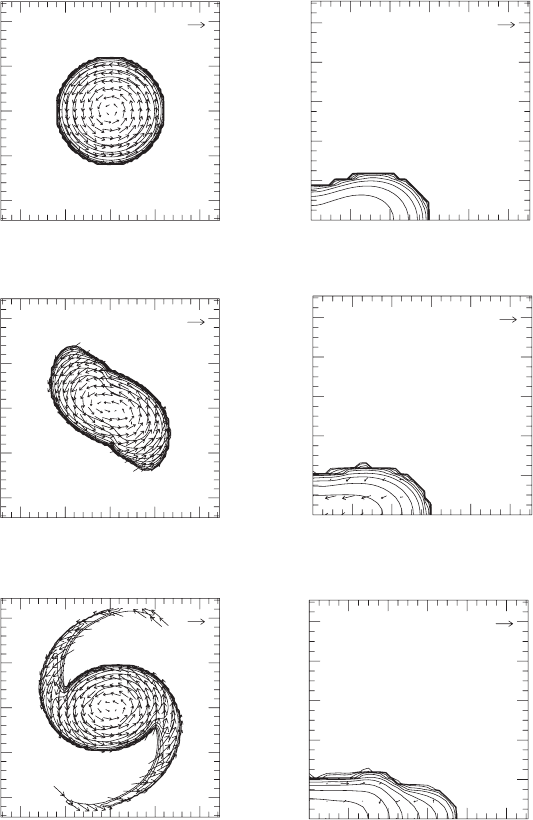
Figure 14.6 Snapshots of contours for the density ρ

∗

and the velocity ﬁeld v

in the equatorial plane (left) and

in the meridional plane (right) for a bar-unstable model with R/M ≈ 7.1andβ ≈ 0.26. The contour lines are

drawn for ρ

∗

/ρ

∗ max

= 10

−0.3 j

for j = 0, 1, 2,...,10 where ¯ρ

∗ max

is 0.126, 0.172 and 0.264 at the three

different times. The lengths of arrows are normalized to 0.3c (left) and 0.1c (right). The time is shown in units of

the initial central period P ≈ 15M.[FromShibata et al. (2000b).]

14.2 Evolution: instabilities and collapse 483

0510

0.3c

0.1c

0.3c

t=0.00P

t=3.07P

t=5.77P

0.3c

X / M X / M

0.1c

Y / M

Z / MZ / M

Z / M

−10

−10 −5

0510

−10 −5

−5

−10

−5

0510

−10 −5

−10

−5

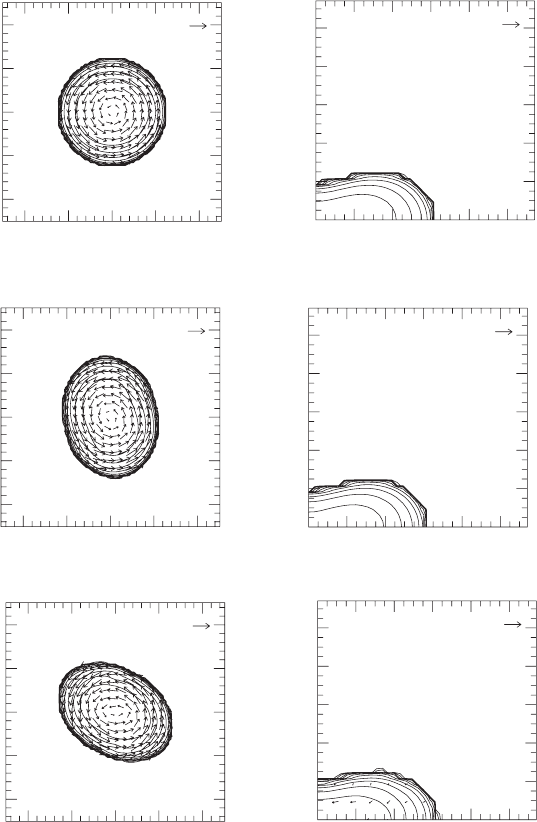
Figure 14.7 Snapshots of contours for the density ρ

∗

and the velocity ﬁeld v

in the equatorial plane (left) and

in the meridional plane (right) for a bar-unstable model with R/M ≈ 7.2andβ ≈ 0.25. The contour lines are

drawn for ρ

∗

/ρ

∗ max

= 10

−0.3 j

for j = 0, 1, 2,...,10 where ¯ρ

∗ max

is 0.128, 0.152 and 0.176 at the three

different times. The lengths of arrows are normalized to 0.3c (left) and 0.1c (right). The time is shown in units of

the initial central period P ≈ 15M.[FromShibata et al. (2000b).]

484 Chapter 14 Rotating stars

As discussed in Chapter 13.1.2, black hole excision exploits the fact that the singularity

resides inside an event horizon, in a region that is casually disconnected from the rest of

the Universe (see Chapter 7.1). Since no physical information can propagate from inside

the event horizon to the outside, we should be able to evolve the exterior independently

of the interior spacetime. This entitles us to “excise” the black hole interior, or that part

of the interior containing the singularity, from the computational domain and evolve the

remaining region alone, without any adverse consequences.

Although it is guaranteed that no physical signal can propagate from inside the horizon

to outside, unphysical signals often can propagate in evolution codes. Gauge modes can

move acausally for many gauge conditions. Although they carry no physical content, such

modes may destabilize the code. Thus, the choice of gauge is crucial to obtaining good

excision evolutions. In addition, constraint-violating modes can, for some formulations of

the ﬁeld equations, propagate acausally, creating inaccuracies and instabilities. Thus, the

choice of formulation is also crucial to obtaining good excision evolutions.

The feasibility of black hole excision was ﬁrst demonstrated in spherically symmetric

1 + 1 dimensional evolutions of a single black hole in the presence of a self-gravitating

scalar ﬁeld.

Excision was also implemented successfully to study the spherically sym-

metric collapse of collisionless matter to a black hole in Brans–Dicke theory.

Since

that time, excision has been used successfully to evolve single and binary black holes in

axisymmetry and full 3 + 1 dimensions.

The ﬁrst implementation of black hole excision

in a 3 + 1 relativistic hydrodynamics code was accomplished by Duez et al. (2004).

Their code evolves the gravitational ﬁeld equations both in axisymmetry and full 3 + 1via

the BSSN formulation. In their original version,

the hydrodynamic equations are evolved

via a Wilson code, using the van Leer algorithm for the advection and artiﬁcial viscos-

ity to handle shocks. Their subsequent version

evolves the ﬂuid equations with a more

sophisticated HRSC scheme along the lines discussed in Chapter 5; it also incorporates

relativistic MHD. Duez et al. (2004) insert additional “constraint damping” terms into the

BSSN ﬁeld equations to help satisfy the constraints numerically and achieve improved

accuracy, a technique we discussed in Chapter 11.5.

This addition consists of modifying

equations (11.50), (11.51) and (11.52) according to

∂

φ =···+c

T αH (14.38)

∂

¯γ

=···+c

T α ¯γ

H (14.39)

∂

=···−c

T α

H, (14.40)

Seidel and Suen (1992).

Scheel et al. (1995a,b).

See Baumgarte and Shapiro (2003c) and Chapter 13 for discussion and references.

See also Baiotti et al. (2005).

Duez et al. (2003).

Duez et al. (2005b).

Detweiler (1987); Frittelli (1997); Alcubierre et al. (2000); Yoneda and Shinkai (2001, 2002); Kelly et al. (2001);

Yo et al. (2002).

14.2 Evolution: instabilities and collapse 485

where T is the time step, c

= 0.1, c

= 0.5, and c

= 1 are dimensionless

coefﬁcients found empirically, and where

H is given by the Hamiltonian constraint

condition (11.48). In a similar spirit, the three BSSN “auxiliary constraint” conditions

0 =

≡



+ ¯γ

, j

(14.41)

0 =

D ≡ det( ¯γ

) − 1 (14.42)

0 =

T ≡ tr(

) (14.43)

are incorporated into the right-hand sides of the evolution equation (11.55)for∂



equation (11.51)for∂

¯γ

andequation(11.53)for∂

, respectively.

The lapse and shift conditions are chosen so that, as the system settles into equilibrium, it

appears stationary in the adopted coordinates. The lapse function is designed to be nonzero

at the apparent horizon in order to maintain “horizon penetration”, i.e., time evolution that

proceeds smoothly across the horizon, without the steep build-up of gravitational waves

and ﬂuid that arises when the lapse and the advance of proper time plummet to zero

there. Horizon penetration allows the location of an excision region inside the horizon; the

evolution equations do not have to be solved inside the excision region. Duez et al. (2004)

report great success with the hyperbolic “driver” conditions

∂

= b

(α∂



− b

∂

), (14.44)

with b

= 0.75 and b

= 0.27M

−1

and

∂

α = αA

∂

A =−a



α∂

K + a



∂

α + e

−4φ

α(K − K

drive

)



. (14.45)

In equation (14.45), the presence of α in front of

A prevents the lapse from dropping to

zero. With this feature, the lapse levels off at ﬁnite positive values everywhere on and

outside the excision zone The term K

drive

is the value to which the mean curvature K

is “driven” at late times. Several choices for K

drive

are useful. The simplest, and usually

adequate choice, is zero. This drives K to zero (maximal slicing) and usually causes a very

slow downward drift in the lapse near the horizon. For many astrophysical applications,

where one only needs to evolve for several hundred M, this drift is usually unimportant.

However, the effect can be removed and horzion penetration maintained by a better choice

of K

drive

. One possibility is K

init

, the value of K at the time excision is introduced. Another

choice is K

, a function which mimics the Kerr–Schild form for K for a Kerr black hole.

The results of the simulations are insensitive to the precise boundary conditions applied

at the edge of the excision zone, as they should be. For example, in their excision code,

Duez et al. (2004) simply copy the time derivatives of ﬁeld quantities onto the excision

See also Alcubierre et al. (2000); Yo et al. (2002).

Alcubierre et al. (2001); cf. the hyperbolic conditions discussed in Chapter 4.3 and 4.5.

See Duez et al. (2004), equation (19)

486 Chapter 14 Rotating stars

boundary from the time derivatives at outer adjacent points. They use spherical excision

regions inside the apparent horizon throughout, although this is not essential.

Tracking the collapse of rapidly rotating stars is one of the most important applications

of black excision. As an example, consider the following issue: if the star collapses to a

stationary black hole in vacuum, the “no-hair” theorem requires that it settle down to a

Kerr black hole. In the Kerr spacetime, the singularity is covered by an event horizon only

if J /M

≤ 1; otherwise the singularity is naked. Rotating stars, on the other hand, are

not so restricted, and sufﬁciently rapidly rotating stars will have J/M

> 1. If the cosmic

censorship hypothesis is true, then the collapse of the whole system must somehow be

averted. How is this guaranteed? One way is if the star loses angular momentum as it

collapses, either by gravitational wave emission

or by shedding matter with high speciﬁc

angular momentum, so that the ﬁnal black hole has J/M

< 1. A naked singularity can

also be averted if the collapse of a J/M

> 1 star is always halted by centrifugal forces, so

there will be no black hole and no singularity at all. It is easy to argue qualitatively

that a

centrifugal barrier will arise to protect cosmic censorship in this way. Assuming no mass

or angular momentum is shed during the collapse, the radius R

at which the centrifugal

force balances the gravitational force will be

∼

, (14.46)

so that

∼





. (14.47)

Hence, if J/M

< 1 (i.e., the star is sub-Kerr), the star will already be inside a black

hole before rotation can halt the collapse. For J/M

> 1 (i.e., the star is supra-Kerr), the

collapse will be halted at a radius larger than M, and no black hole forms.

Simulating gravitational collapse of rotating objects and rigorously checking whether

or not it complies with the Kerr limit for black hole spin has been done for representative

cases of ﬂuid stars

and collisionless clusters.

For some cases, the simulations did not

(and sometimes could not) study in detail the ﬁnal fate of the conﬁguration or the outgoing

gravitational radiation ﬂux when a black hole forms. In hydrodynamic collapse, this is

often the situation when the EOS is soft and the initial star is extended in size ( M)

and centrally condensed, or when there is signiﬁcant rotation to hold back the outer layers.

Eventually, grid stretching, the collapse of the lapse, or some other complication in the

vicinity of the black hole arises to terminate the integration before the outer layers have

completed their evolution. Excision, which is designed to overcome this complication,

enables one to address the issue of sub-Kerr vs. supra-Kerr collapse and identify the ﬁnal

But recall that in axisymmetry, no angular momentum is carried off by gravitational waves during collapse; see, e.g.,

Lightman et al. (1975), Problem 18.9.

Nakamura (2002).

Nakamura and Sato (1981); Stark and Piran (1985); Shibata (2000).

Abrahams et al. (1994); see the discussion in Chapter 10.4.

14.2 Evolution: instabilities and collapse 487

state. Such an algorithm is useful not simply for determining whether or not a black hole

forms, but also for determining how much rest mass and gravitational energy escapes

collapse if it does.

To explore this cabability with their excision algorithm, Duez et al. (2004) employed

the routine of CST to construct three differentially rotating n = 1 polytropes of the same

rest mass but varying spin to obtain both sub-Kerr and supra-Kerr models for initial data.

Following pressure depletion to trigger their collapse, they tracked the adiabatic evolution

of these conﬁgurations in axisymmetry on grids of 300

to 400

zones. Two of their models,

stars A and B, are sub-Kerr (J /M

= 0.57 and 0.91, respectively) and collapse to Kerr

black holes without disks. In the case of star B, a nearly spherical apparent horizon forms

at t/M = 28.4 at a coordinate radius of r

/M = 0.62. Excision is introduced inside

/M = 0.08 at t = 29M, at which time 22% of the rest mass is outside the excision

zone, and 15% is outside the apparent horizon. All of the matter falls into the hole within

20M after excision is introduced, but the evolution is continued for an additional 20M

after this. No instabilities arise and the system evolves to a stationary state. A third model,

star C, is supra-Kerr (J/M

= 1.2). Following an initial implosion, the core of this star

hits a centrifugal barrier, rebounds, and drives a shock into the infalling outer region. The

star then expands into a torus and undergoes damped oscillations, settling down to a new

stationary, nonsingular equilibrium state (a hot, rotating star), with nearly the same mass

and angular momentum as the original star.

For the above class of initial data leading to collapse, not only is cosmic censorhip

obeyed, but the spin parameter J/M

of the progenitor seems to provide a unique indicator

of the ﬁnal fate: if the spin is less than the Kerr limit, a black hole forms, otherwise there is

no black hole but a new, nonsingular, equilibrium state. The situation is more complicated

in general. Consider, for example, the fate of marginally unstable, rigidly rotating poly-

tropes with n slightly above 3. Such stars crudely model the cores of massive stars in which

thermal instabilities (e.g., iron photodissociation, or pair annihilation) are present to drive

the adiabatic index slightly below 4/3 at the endpoint of stellar evolution. Consequently,

tracking their collapse and determining their ﬁnal fate is important astrophysically. Sim-

ulations of adiabatic collapse in axisymmetry by Shibata (2004) show that J/M

again

proves to be a good predictor of the ﬁnal outcome. But now a black hole may form even

for 1

∼

J/M

∼

2.5; only for J/M

∼

2.5 does a centrifugal barrier prevent the direct

formation of a black hole. For cases in which J/M

exceeds unity but a black hole forms,

the effective value of the spin parameter in the central region of the progenitor is smaller

than unity. The outcome is then a rapidly rotating black hole surrounded by a massive, hot,

equilibrium disk.

Uniformly rotating n = 3 polytropes revisited

As we remarked in Section 14.2.1, the simulation of the collapse of a marginally unstable

n ≈ 3 rotating polytrope from the point of onset of radial instability to ﬁnal stationary

488 Chapter 14 Rotating stars

equilibrium is computationally challenging, even when restricting the analysis to axisym-

metry. The reason, as we discussed, is dynamic range. In addition, even after the issue of

dynamic range is resolved by a suitable spatial grid algorithm, black hole excision must

be utilized in order that the simulation be able to reach the ﬁnal, stationary, dynamical

equilibrium state. In the presence of viscosity or magnetic ﬁelds, gas accretion from the

disk onto the black hole will continue on a secular (i.e., viscous, or magnetic) time scale

even after dynamical equilibrium is achieved. Reaching this dynamical equilibrium state,

and then following the quasisteady accretion and secular growth of the black hole, clearly

requires black hole excision.

The axisymmetric simulation of the adiabatic collapse of a marginally unstable n = 3

polytrope rotating uniformly at the mass-shedding limit performed by Shibata and Shapiro

(2002) and discussed in Section 14.2.1 was repeated by Liu et al. (2007), who used black

hole excision toward the end of the simulation to reach a ﬁnal stationary equilibrium state.

This simulation employed the basic BSSN, HRSC code of Duez et al. (2005b), using up

to 1400

grid points and adopting the same rezoning technique as Shibata and Shapiro

(2002) to handle the early Newtonian phase of the collapse. However, a transformation

from the original set of coordinates (

z), with

r = (

)

1/2

and uniform grid

spacing 

, to new, radially “squeezed” coordinates (x, y, z) with r = (x

+ y

+ z

)

1/2

and nonuniform grid spacing, was performed at late times to improve further the resolution

near the black hole:

r ≈ (dr/d

r)

r,wheredr/d

r was constructed to equal ≈ 1/8 near

the hole, rising continuously to unity far away.

Most importantly, black hole excision was

introduced soon after the appearance of an apparent horizon, and the simulation continued

for an additional interval of time after this. The results are summarized in Figures 14.8,

14.9 and 14.10.

The pre-excision evolution from the onset of collapse to the appearance of an apparent

horizon takes a total coordinate time t/M ≈ 28 284 and requires 32 520 Courant time

steps. The post-excision evolution lasts only t/M ≈ 2220, but requires about 18 000

additional time steps, due to the smaller grid spacing at late times. At t/M ≈ 219 after

the onset of the excision, gravitational ﬁeld evolution is “turned off” and the metric is

frozen while the hydrodynamic evolution of the residual matter continues until the end

of the simulation. Holding the metric (i.e., gravitational ﬁeld) ﬁxed as the matter evolves

is referred to as the “Cowling approximation”. It is justiﬁed whenever the gravitational

ﬁeld settles into a quasistationary state, which is the case here. In the adopted gauge, the

apparent horizon ﬁrst appears at r

/M ≈ 0.46 and grows to r

/M ≈ 1.6 by the end

of the post-excision evolution. The excision radius is initially set to r

/M ≈ 0.77 and is

increased to r

/M ≈ 1.1byt/M ≈ 100 after the start of excision, after which it is held

ﬁxed. The outer boundary is moved inward to L/M ≈ 58 at late times. About 1% of the

rest-mass and 5% of the angular momentum is lost to regridding.

This simple version of FMR is known as “multiple-transition ﬁsheye” coordinates; see Campanelli et al. (2006a).

The resulting radial grid spacing becomes r ≈ 0.025M for r

∼

4M and rises to r ≈ 0.2M for r

∼

22M; the outer

boundary is near 60M.

14.2 Evolution: instabilities and collapse 489

600

500

400

300

200

t = 0

0.2c

Z / M

X / M X / M X / M

X / M

t − t

= 51.7 M

t − t

= 174.8 M

t − t

= 2151 M

t = 25260M

0.02c

0.1c

t = 28284M

100

150

100

0 50 100 150 200

100

302015 251050

100 200 300 400 500 600

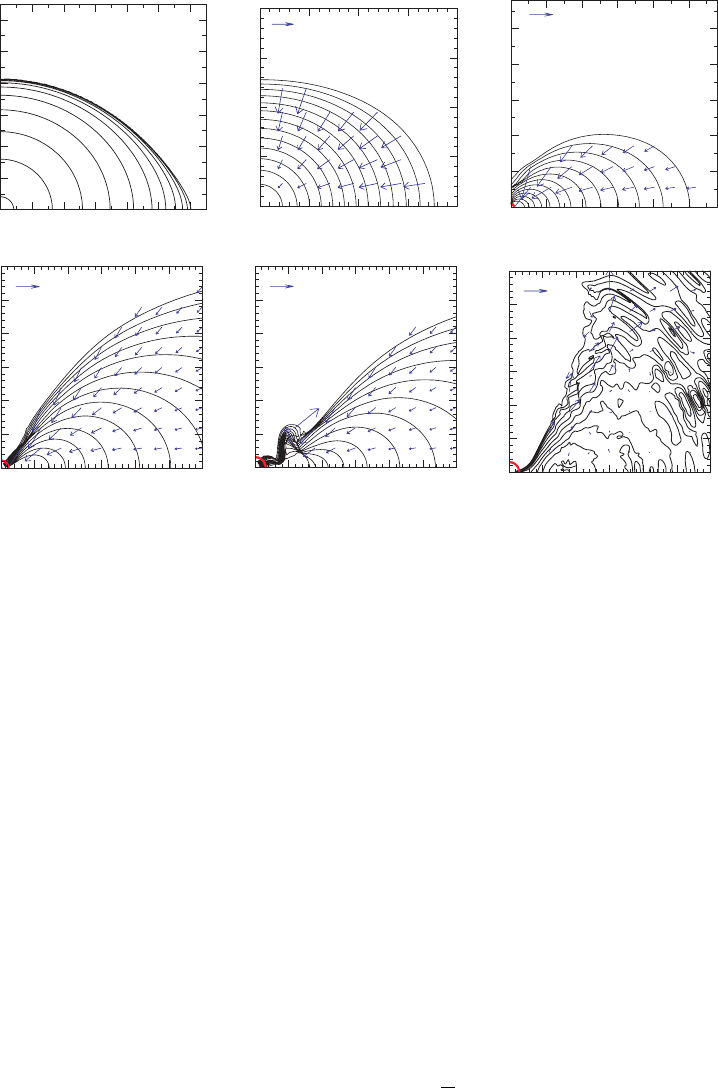
Figure 14.8 Snapshots of meridional rest-mass density contours and velocity vectors at selected times for n = 3

collapse. The initial model is rotating uniformly near the mass-shedding limit at the onset of gravitational

instability to collapse. The density contour curves are drawn as follows: (a) Pre-excision top row, at t = 0,

= 10

−j−0.1

(0) with j = 0, 1,...,10, where ρ

(0) is the initial central density; at t = 25 260M,

= ρ

scal

−0.3 j

( j = 0−12), where ρ

scal

= 11ρ

(0) and at t = 28 284M, ρ

scal

= 1000ρ

(0). (b) Post-excision

bottom row, ρ

= 100ρ

(0)10

−0.3 j

( j = 0−10). The thick solid (red) curve denotes the apparent horizon. For

post-excision evolution, time is measured from the beginning of excision (t

= 28 284M). Note that the

coordinate scale decreases as time increases to show the central region in detail. [After Liu et al. (2007).]

Figure 14.8 shows the formation of a hot, thick disk about the black hole at late times.

Figure 14.9 zooms into the region near the black hole at the end of the simulation and

shows the relative scale of the excision zone, apparant horizon. and inner disk. Figure 14.10

plots the time evolution of several key parameters characterizing the hole. The irreducible

mass M

irr

is calculated from equation (7.2), using the area of the apparent horizon, which

should coincide with the event horizon at late times. The black hole angular momentum is

calculated from

= J − J

matter

(r > r

) (14.48)

where the angular momentum of the matter outside the horizon is given by

matter

(r > r

) =



r>r

√

γ d

x, (14.49)

490 Chapter 14 Rotating stars

X / M

t − t

= 2151M

Z / M

0.1c

Figure 14.9 Blow-up of the meridional rest-mass density contours and velocity vectors at the end

of the simulation, following excision and Cowling evolution. The density contours are drawn for

= 100ρ

(0)10

−0.3 j

( j = 0−10). The thick solid (red) curve denotes the apparent horizon, and the dark region

denotes the excision zone. [After Liu et al. (2007).]

0.9

0.8

0.7

0.6

irr

disk

/ M

0.5

0.4

0.3

0.2

0.1

30 60

(t − t

)/M

90 120 150 180

Figure 14.10 Post-excision evolution of the horizon mass M

, spin parameter J

, the irreducible mass M

irr

of the central black hole, and the rest mass of the disk M

disk

outside the apparent horizon. Time is measured from

the beginning of excision (t

= 28 284M). [From Liu et al. (2007).]

in accord with equation (14.22). Then, to estimate the black hole mass M

, we can use

equation (7.3). This relation is only approximate for this spacetime, which consists of a

rotating black hole and an ambient disk, and is exact only for a vacuum Kerr spacetime.

From this we estimate the black hole spin parameter, J

. The ﬁgure shows that the loss

of rest mass in the disk due to ﬂow into the black hole reduces to a trickle by t/M

∼

150