Басниев К.С. Энциклопедия газовой промышленности

Подождите немного. Документ загружается.

ОБЩИЕ СВЕДЕНИЯ

1.2.3.7. Наиболее употребительные

асимптотические

разложения

В окрестности нуля:

(1±х)

(т>0)

±тх+

lx2±

.,,

,,»-U(/n-2)

+ ...+ (±1)'

(m>0)

m(m+1)

, m(m

1)(m+2)

1ттх+

—2|—^

m(m+1)

...i

sin

x =

cosx

tgx=

1.2.4.

Матрицы

1.2.4.1.

Определение

Матрица

вида л х т есть

система

лхт чисел,

расположенных в виде прямоугольной таблицы из

л строк и т столбцов:

А =

... a

врэ

... a

;

1т

2т

... а

а,

У-I.m

1.2.4.2. Частные случаи

Если

л = 1, получается матрица-строка или век-

тор-строка:

Х-||х,

Если

т = 1, имеем матрицу-столбец или вектор-

столбец:

Если

п,

получаем квадратную матрицу:

n a

... a

2п

•••

а,

1/»1,л

У" 1.л

Различают несколько

специальных

типов

квад-

ратных

матриц:

— квадратная матрица А симметрична, если а

= а/

для

любых

/и у, 1 £ iu л, 1 £/£ л;

— квадратная матрица А диагональна, если a

= 0

при/*/:

А =

a,, 0 0 ... 0

a^ 0 ... О

О О ею ... О

О О О ... а„„

Если, к тому же, а

= а^ =... = а

да

»1, получается

единичная или тождественная матрица:

— квадратная матрица А называется верхней тре-

угольной,

если a

в 0 при / > у,

— квадратная матрица А называется нижней тре-

угольной,

если щ - 0 при / < у.

1.2.4.3. Транспонированная матрица

По определению, транспонированной по отно-

шению к матрице

А =

Ца

/у

||,.,

У-1,т

вида пх т называется матрица

/-1.Л

вида т х п (строки матрицы А становятся столбца-

ми

матрицы 1д).

Квадратная матрица А симметрична в том и

только

в том случае, когда t

= A.

1 ОБЩИЕ СВЕДЕНИЯ

1.2.4.4.

Сумма

двух

матриц

Пусть

А =

||««II,-,.„.

1-1,т

||Ь,

||,

ж1>л

1-1. т

две матрицы одинаковой формы. Их сумма

С = А + В - это матрица

7-1,т

определенная равенствами

1.2.4.5.

Произведение

двух

матриц

Чтобы

произведение АВ

двух

матриц А и В имело

смысл, требуется совпадение числа столбцов пер-

вой матрицы А с числом строк второй матрицы В.

У=1.Р

Произведение С = АВ есть матрица вида пхр:

7-1.Р

определенная соотношениями

fc-1

[pij

- это скалярное произведение /-ой строки А на

/•ый столбец В).

Важное замечание:

Может

случиться, что произведение АВ опреде-

лено, а произведение ВА - нет. Более того, даже

если существуют оба произведения одновременно,

они вообще говоря, не

равны:

АВ

ВА.

1.2.4.6.

Произведение матрицы на

действительное

число

Пусть

даны

матрица А = ||а,у||

/=1 п

и действи-

7=1,m

тельное

число

Произведение В = ЯА есть матрица

У=1,т

определенная равенствами Ь, =

Xa,j.

1.2.4.7.

Система

линейных

уравнений.

Линейное преобразование

отождествляется с матричным уравнением АХ = Y,

где

/-1.

есть матрица системы,

X =

Y =

- вектор-столбец неизвестных,

- вектор-столбец

правых

частей

Матрицу

А можно также рассматривать как мат-

рицу линейного преобразования, переводящего

вектор X в вектор Y в векторном пространстве раз-

мерности л.

1.2.4.8.

Обратная матрица

Пусть

А = If а

/у

||,_

„ - квадратная матрица по-

У-1.п

рядка

л, а

0 ... О

1 ... О

О 0 ... 1

- единичная матрица порядка л.

Обратной по отношению к матрице А называет-

ся такая матрица порядка л, которая обозначается

А"

и удовлетворяет соотношениям АА"

= А~

А = I.

Матрица

А, для которой обратная матрица не су-

ществует, называется особой (или вырожденной).

Рассмотрим линейную систему с матрицей А:

— если А обратима (т.е. имеет обратную матрицу),

то система АХ = Y допускает единственное ре-

шение

X = A"

— если А - особая, то система не имеет решений

или имеет их неограниченное количество.

1.2.4.9.

Определитель матрицы

Пусть

А = ||а,у||

/=1 п

- квадратная матрица по-

7-1.

рядка л.

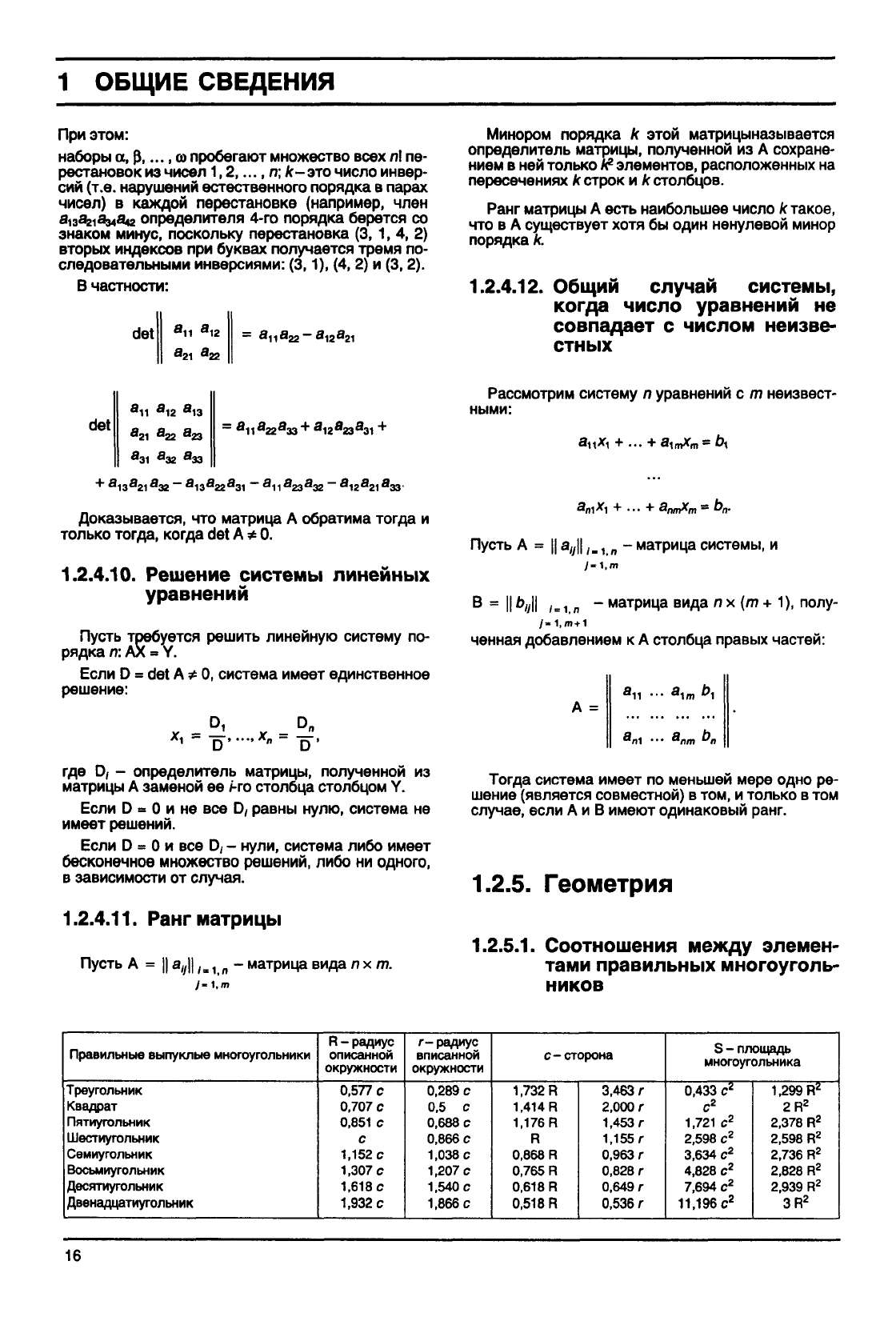
Определителем D матрицы А называют число,

равное

Х(-1)*а

1а

гр

...а

П(В

Линейная система л уравнений с л неизвестными:

обозначаемое

= det A =

... а

1л

1 ОБЩИЕ СВЕДЕНИЯ

При

этом:

наборы а, р со пробегают множество всех л! пе-

рестановок из чисел

1,2,...,

л; к- это число инвер-

сий (т.е. нарушений естественного порядка в парах

чисел) в каждой перестановке (например, член

£>1з%1

^34^42

определителя 4-го порядка берется со

знаком

минус, поскольку перестановка (3, 1, 4, 2)

вторых

индексов при буквах получается тремя по-

следовательными инверсиями:

(3,1),

(4, 2) и (3, 2).

В частности:

det

—

22~

Минором порядка к этой матрицыназывается

определитель матрицы, полученной из А сохране-

нием

в ней только к

элементов, расположенных на

пересечениях к строк и к столбцов.

Ранг матрицы А есть наибольшее число

/с

такое,

что в А существует хотя бы один ненулевой минор

порядка к.

1.2.4.12.

Общий случай системы,

когда

число уравнений не

совпадает с числом неизве-

стных

det

зЗ

ЗЗ

32 ~

Доказывается, что матрица А обратима тогда и

только

тогда, когда det А * 0.

1.2.4.10.

Решение системы линейных

уравнений

Пусть требуется решить линейную систему по-

рядка л: АХ = Y.

Если D = det А

0, система имеет единственное

решение:

где

D, - определитель матрицы, полученной из

матрицы А заменой ее /-го столбца столбцом Y.

Если D • 0 и не все D,

равны

нулю, система не

имеет

решений.

Если D = 0 и все D; - нули, система либо имеет

бесконечное множество решений, либо ни одного,

в зависимости от случая.

1.2.4.11.

Ранг матрицы

Пусть

А =

a,j\\

1ш

, „ - матрица вида пхт.

У-1,т

Рассмотрим систему л уравнений с т неизвест-

ными:

a,,*,

Пусть А =

а,

||,. ,

- матрица системы, и

У-I.m

В =

/у

1шЛ п

- матрица вида пх(т + 1), полу-

уж 1,m+1

ченная добавлением к А столбца

правых

частей:

А =

•••

1/п

Тогда система имеет по меньшей мере одно ре-

шение

(является совместной) в том, и только в том

случае, если А и В имеют одинаковый ранг.

1.2.5.

Геометрия

1.2.5.1.

Соотношения между элемен-

тами

правильных

многоуголь-

ников

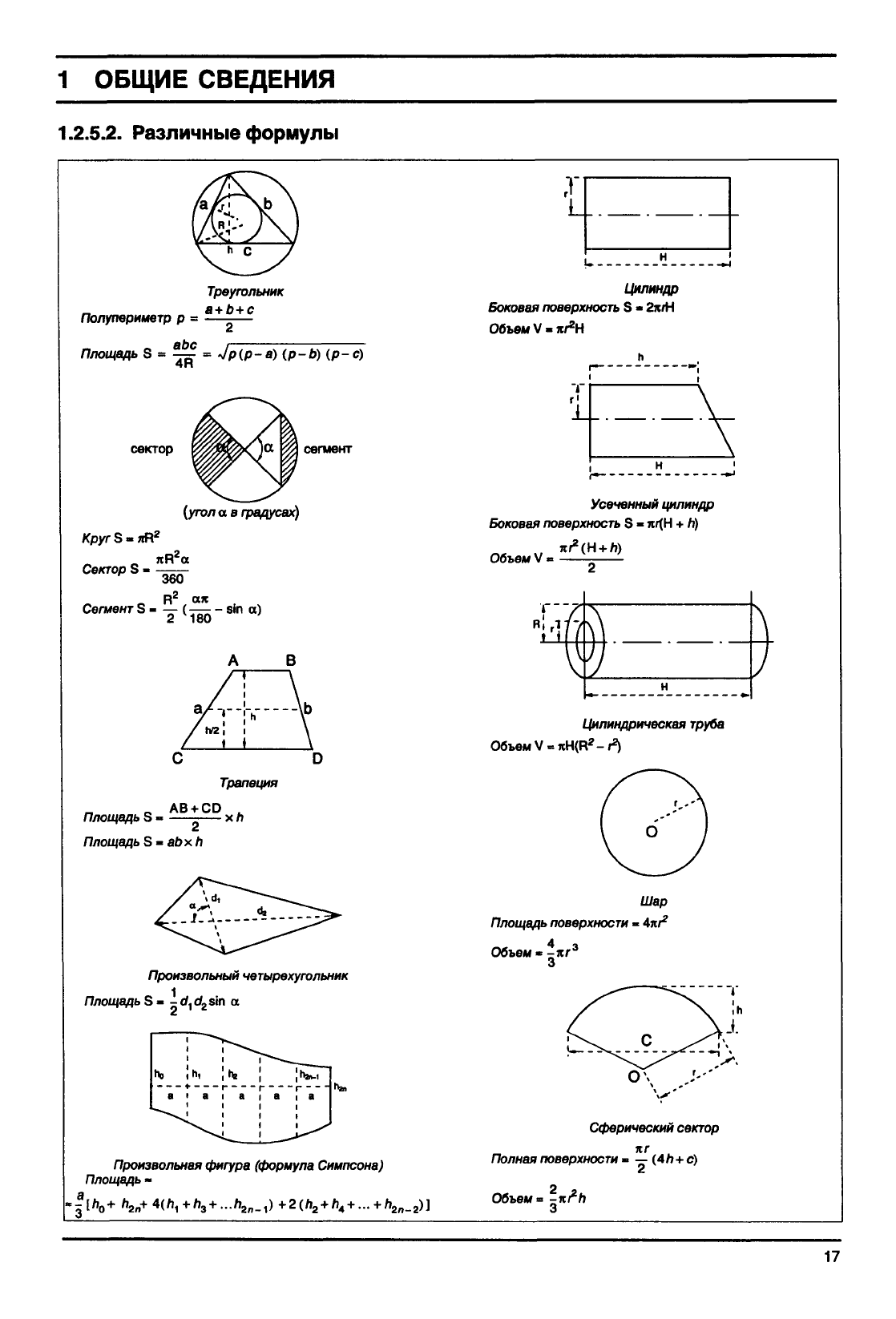
Правильные

выпуклые

многоугольники

Треугольник

Квадрат

Пятиугольник

Шестиугольник

Семиугольник

Восьмиугольник

Десятиугольник

Двенадцатиугольник

R - радиус

описанной

окружности

0,577

0,707

0,851

1,152

1,307

1,618

1,932

г-радиус

вписанной

окружности

0,289

0,5

0,688

0,866

1,038

1,207

1,540

1,866

с-сторона

1,732

1,414

1,176

0,868

0,765

0,618

0,518

3,463

2,000

1,453

1,155

0,963

0,828

0,649

0,536

S- площадь

многоугольника

0,433

1,721

2,598

3,634

4,828

7,694

11,196

1,299

2,378

2,598

2,736

2,828

2,939

ОБЩИЕ

СВЕДЕНИЯ

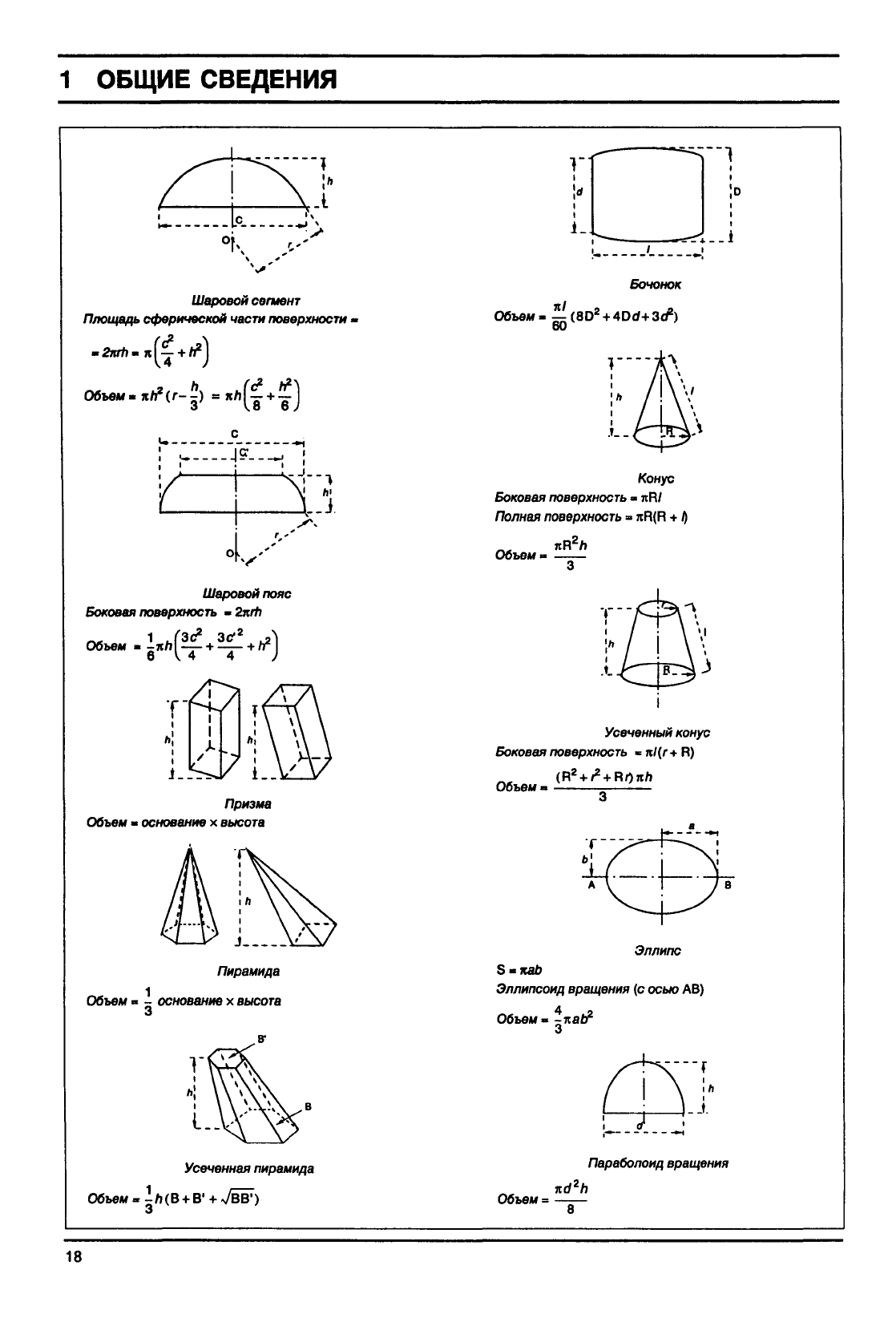
1.2.5.2.

Различные

формулы

Полупериметр

р =

Треугольник

а + Ь+с

Площадь

s = — =

Jp(p-a)

(р-Ь) (р-с)

сектор

сегмент

(угол

а в

градусах)

Круг

S-kR

Сектор

S -

360

Сегмент

S-—(^-sin

ал-г

С D

Трапеция

AB+CD

Площадь

S — х h

Площадь

S ~

abxh

Произвольный

четырехугольник

Площадь

S - -

sln

Произвольная

фигура

(формула

Симпсона)

Площадь

и 1

Цилиндр

Боковая

поверхность

S » 2я/Н

Объем

г'

Усеченный

цилиндр

Боковая

поверхность

S - я^Н + h)

Объем

"id/"'

Цилиндрическая

труба

Объем

Шар

Площадь

поверхности

- Лш

Объем.-яг

Сферический

сектор

яг

Полная

поверхности

- — (4Л+ с)

Объем

-я/

/»

ОБЩИЕ СВЕДЕНИЯ

Шаровой

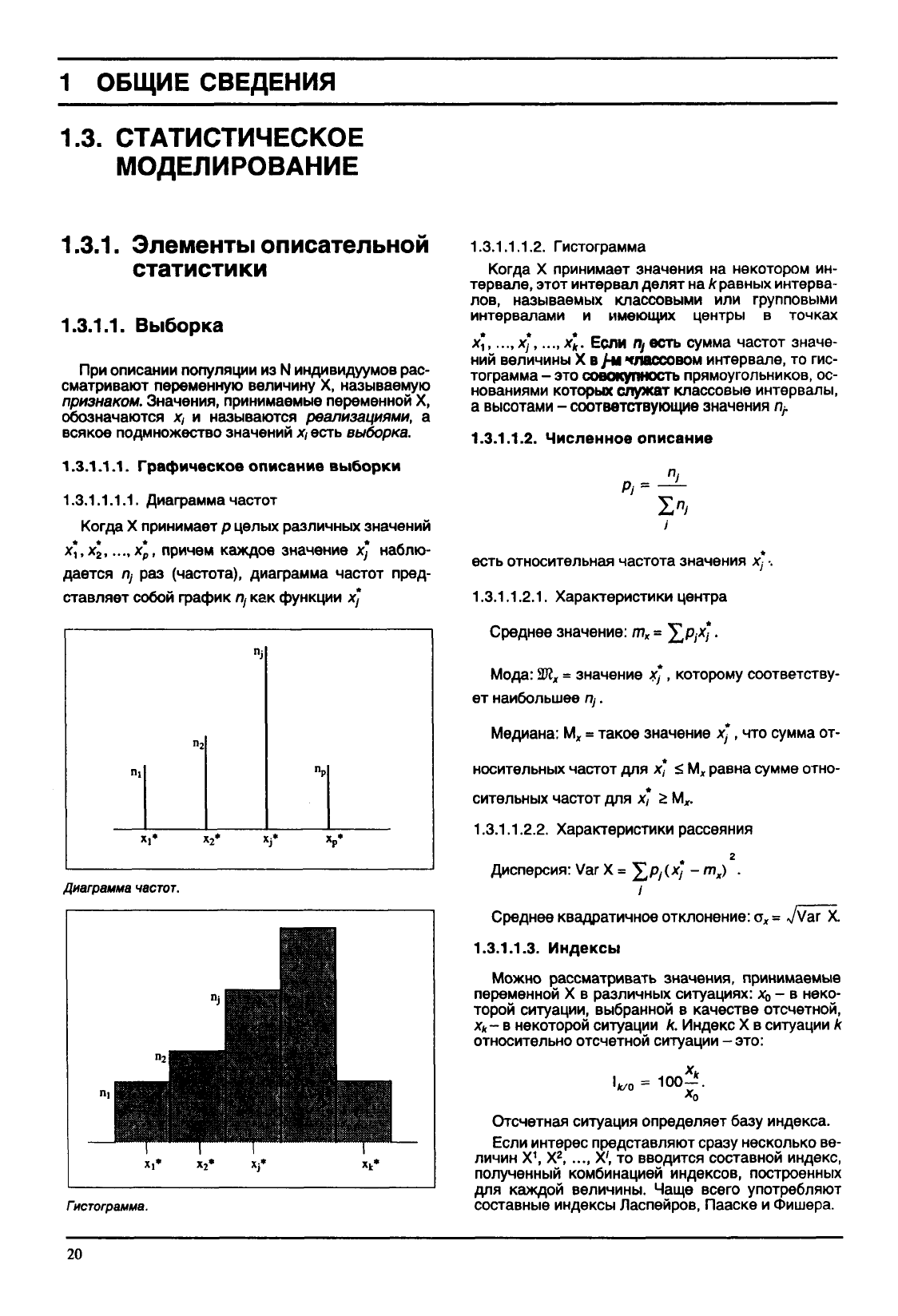
сегмент

Площадь

сферической

части

поверхности

•

Объем

ш nh

(г--) =

яЛ

(т

'в"

Зз

Шаровой пояс

Боковая

поверхность

Призма

Объем

основание

высота

Объем

= -

основание

высота

L-V

Усеченная

пирамида

Бочонок

Объем- ^(8D

4Dd+3o

)

Конус

Боковая

поверхность

» nR/

Полная

поверхность

=•

nR(R + /)

Объем

•

яй

/»

Усеченный

конус

Боковая

поверхность

л/(г+

Объем «

Эллипс

S-каЬ

Эллипсоид

вращения

(с

осью

АВ)

Объем»

-nab

Параболоид

вращения

Объем-

1 ОБЩИЕ СВЕДЕНИЯ

1.2.6.

Численные методы

Некоторые

вычисления

не могут

быть

выполне-

ны с абсолютной точностью. Поэтому для решения

соответствующих задач необходимо применять

численные методы, которые реализуются с по-

мощью программ для ЭВМ. Ниже описываются не-

которые основные численные методы.

1.2.6.1.

Численное интегрирование

Чтобы

вычислить

/£x)dx,

делим интервал [а, Ь]

на 2л

равных

интервалов, получая точки деления

ль » а, х, = а + л,..., Хал = а + 2nh • Ь.

Формула Симпсона (точность которой возраста-

ет

с ростом л):

1.2.6.2.

Решение системы

линейных уравнений

Пусть требуется решить систему

п1

х, + ...

Опишем

метод исключения Гаусса.

Предполагая,

что а„ * 0, заменим исходную сис-

тему

эквивалентной системой

х =

a\p = a

——- и Ь,

<1>

= b,——-, полученной

исключением неизвестного х, из уравнений с номе-

рами

от 2 до п.

Повторяя эту процедуру п - 1 раз, придем к эк-

вивалентной треугольной системе

... + а

1п

х„ = Ь\

_(П-1)

_ «.(Л-1)

n~ °n >

в которой коэффициенты даются реккурентными

формулами:

_<*-1)_<*-1)

<*>

(*-1)

'»

кк

ДЛЯ /=к+1,...

Затем

решаем треугольную систему, рассмат-

ривая последовательно уравнения от последнего к

первому, что дает:

Числа а,,, а^, а^, ... фигурирующие в рекку-

рентных формулах, называются ведущими элемен-

тами.

Они предполагаются отличными от нуля: ес-

ли по ходу решения возникает нулевой ведущий

элемент,

то соответствующее уравнение меняют

местами

с одним из следующих так,

чтобы

полу-

чить

ведущий элемент, не

равный

нулю.

1.2.6.3.

Решение системы

нелинейных уравнений

Пусть требуется решить систему нелинейных

уравнений

...,x

)

= 0,

которую мы запишем в виде F(x) = 0 с X

•

Метод

Ньютона-Рафсона состоит в последова-

тельном вычислении, исходя из некоторого на-

чального вектора

Х°

векторов

Х\Х

, ...Х

х™

определяемых реккурентным соотношением

J(X'")(X

m+1

- X"

) = -FfX"

есть якобиан F в точке Х

3f,

Эх,

э/,

"• Эх

кк

ЭТОТ

алгоритм сходится, т.е. Х

стремится к ре-

шению

системы при т, стремящемся к бесконечно-

сти,

если

только

Х° есть "не слишком плохое" при-

ближение

решения.

ОБЩИЕ СВЕДЕНИЯ

1.3.

СТАТИСТИЧЕСКОЕ

МОДЕЛИРОВАНИЕ

1.3.1.

Элементы описательной

статистики

1.3.1.1.

Выборка

При описании популяции из N индивидуумов рас-

сматривают переменную величину X, называемую

признаком.

Значения, принимаемые переменной X,

обозначаются х, и называются реализациями, а

всякое

подмножество значений х, есть выборка.

1.3.1.1.1.

Графическое описание

выборки

1.3.1.1.1.1.

Диаграмма частот

Когда

X принимает р

целых

различных значений

х\,х\,.... х*, причем каждое значение х* наблю-

дается Лу раз (частота), диаграмма частот пред-

ставляет собой график

Лу

как функции х*

X,« J

'j*

Диаграмма

частот.

1.3.1.1.1.2. Гистограмма

Когда

X принимает значения на некотором ин-

тервале, этот интервал

делят

на к равных интерва-

лов, называемых классовыми или групповыми

интервалами и имеющих центры в точках

х\,...,х],...,х\. Если л)есть сумма частот значе-

ний

величины X в

J-ы

классовом интервале, то гис-

тограмма

- это совокупность прямоугольников, ос-

нованиями которых служат классовые интервалы,

а высотами - соответствующие значения Лу.

1.3.1.1.2.

Численное описание

есть относительная частота значения х*-.

1.3.1.1.2.1.

Характеристики центра

Среднее значение: т

Мода:

2ГС

= значение х*, которому соответству-

ет наибольшее щ.

Медиана: М

= такое значение х*, что сумма от-

носительных частот для х* й М

равна сумме отно-

сительных частот для х, £ М

1.3.1.1.2.2. Характеристики рассеяния

Дисперсия:

Var X

- т„)

Гистограмма.

Среднее квадратичное отклонение: о

JVar

1.3.1.1.3.

Индексы

Можно

рассматривать значения, принимаемые

переменной X в различных ситуациях: х

- в неко-

торой

ситуации, выбранной в качестве отсчетной,

- в некоторой ситуации к. Индекс X в ситуации к

относительно отсчетной ситуации -это:

"*/о = 100-*.

Отсчетная

ситуация определяет базу индекса.

Если

интерес представляют сразу несколько ве-

личин X

, X

X', то вводится составной индекс,

полученный комбинацией индексов, построенных

для каждой величины.

Чаще

всего употребляют

составные индексы Ласпейров, Пааске и Фишера.

ОБЩИЕ СВЕДЕНИЯ

1.3.1.1.4.

Оценки

Параметры, характеризующие распределение

переменной X, обычно бывают неизвестны. Их ста-

раются оценить с помощью функций элементов х,

выборки.

Подобные оценки называются

статисти-

ками.

Так, математическое ожидание Е(Х) оценивает-

ся средним значением m

1.3.1.2.

Двумерная выборка

Чтобы

изучить связь между переменными X и Y,

рекомендуется изобразить на плоскости точки

(X/, yj).

Если

полученное таким образом облако то-

чек имеет удлиненную форму, следует вычислить

коэффициент линейной корреляции:

P(X,Y)

COV(X,

1.3.1.4.1.

Факторные методы

В этих методах

выявляются

соотношения близо-

сти

между индивидуумами, которые распределя-

ются по классам соседних элементов. Для описа-

ния числовых таблиц используется анализ

главных

компонент.

Анализ

соответствий позволяет описы-

вать

зависимость между двумя качественными

признаками.

1.3.1.4.2.

Классификационные методы

В этих методах используются различные алго-

ритмы построения классов или путем последова-

тельных

объединений (восходящие алгоритмы) или

путем разделений (нисходящие алгоритмы).

1.3.2.

Статистические

решения

где

COV(X,Y)

(у

т,)

- ковариация X и Y,

л^-

число точек с координатами (x

у,).

Если

связь между X и Y линейна, то

|р|

= 1. Вы-

численное значение р - это показатель тесноты

связи

между X и Y, но интерпретация этого значе-

ния часто

бывает

затруднена, поскольку указан-

ная связь возмущается связями между последова-

тельными значениями х, или значениями y

, когда

приходится иметь дело с временными рядами.

1.3.1.3.

Случай временных рядов

Так называются числовые последовательности

наблюдений х(Л, упорядоченные во времени, при

1-1,2 Т.

Временной ряд

обладает

памятью, которая

характеризуется последовательностью коэффи-

циентов автокорреляции порядка т = 1, 2,...

СОУ(х(0,л(г+т))

р(т)

График функции р(х) представляет собой

корре-

лограмму.

1.3.1.4.

Исследование числовых

таблиц:

многомерный

анализ

Таблица

из л строк и р столбцов объединяет зна-

чения р признаков, наблюденные на л индивидуу-

мах. Существуют два больших семейства методов

анализа этих таблиц.

1.3.2.1.

Случайная величина

Всякая мера величины, значения которой

зави-

сят от случая, есть

случайная

величина.

Случай-

ная величина называется дискретной, если она

имеет конечное или бесконечное, но счетное коли-

чество возможных значений.

Если

множество ее

возможных значений есть интервал, то говорят,

что

случайная

величина непрерывна.

Случайная

величина X определяется своей

функцией распределения F(x) = Р(Х й х) (вероят-

ность

того,

что X принимает значения, меньшие х).

Если

F(x) непрерывна и дифференцируема, плот-

ностью распределения вероятностей называют

производную

f(x) функции F(x).

1.3.2.1.1.

Примеры дискретных

случайных

величин

1.3.2.1.1.1.

Величина В, распределенная по бино-

миальному закону

Для индивидуума популяции имеются две воз-

можности

А и А, вероятности которых р и 1 - р по-

стоянны в серии из л независимых испытаний

(выбор с возвращением).

1.3.2.1.1.2. Величина Н, распределенная по

гипер-

геометрическому

закону

В популяции из N индивидуумов имеются две

возможности

А и А, вероятности которых меняют-

ся в зависимости от испытания в серии из п после-

довательных

испытаний (выбор с возвращением).

1.3.2.1.1.3. Величина Р, распределенная по закону

Пуассона

В данной популяции признак А появляется с ма-

лой вероятностью р. Реализуется большое число л

независимых испытаний, так что лр = т.

ОБЩИЕ СВЕДЕНИЯ

1.3.2.1.2.

Пример непрерывной случайной

величины

Величина N, распределенная по нормальному

закону

(закону Лапласа-Гаусса).

Изучаемая

величина

В(л,

р)

H(N,

n, р)

Р(т)

Щт, о)

Закон

распределения

вероятностей

Р(Х

= х) = С„р^1

-р)

Р(Х

— jrt —

x-m »

^/5лa

Е(Х)

пр

Var(X)

пр(1

- р)

пр(1-р)

Основные случайные величины.

Изучаемая

величина

H(N,

п.р)

В(л,

р)

В(ар)

Р(т)

Условия приближения

N»n

пр£5

np(1

-p)Z-\8

Л7218

Приближение

В(ар)

P(m=np)

Приближение

случайных

величин.

1.3.2.2.

Критерий согласия

(хи-квадрат) между законом

распределения

вероятностей

и выборкой

Вычисляется количество

пр,

п - объем выборки,

к - число классовых интервалов,

Pi - вероятность попадания в интервал (/) в соот-

ветствии с распределением вероятностей Р,

л,

- число элементов выборки, попадающих в ин-

тервал

(/).

Вычисленное значение D сравнивают с величи-

ной,

называемой х

и соответствующей той малой

вероятности,

которая не должна

быть

превышена.

Решающее правило таково:

если D й х

, принимается гипотеза о том, что изу-

чаемое явление согласуется с законом распреде-

ления

вероятностей Р;

если D > х

. эта гипотеза о согласовании изучае-

мого

явления

с законом распределения вероятнос-

тей Р отбрасывается.

1.3.2.3.

Параметрические

статистические

критерии

Формулируются

две альтернативные гипотезы

и Hi по поводу закона распределения вероятно-

стей

Р. Исследование выборки позволяет сделать

выбор между двумя гипотезами, правда, с риском

ошибиться.

Возможны следующие ситуации:

Реальное

положение вещей

Но

верно

Н,

верно

Заключение

критерия

Принятие

Но

Отбрасы-

вание

Заключение

правильное

Заключение

ложное,

ошибка

первого

рода

Заключение

ложное,

ошибка

второго рода

Заключение

правильное

а фиксировано, а Р вычисляется в предположе-

нии

Hi.

Вероятность отбросить Н

, когда Н

ложно, опре-

деляет

мощность критерия: 1 - р.

1.3.2.4.

Непараметрические

критерии

Эти критерии не относятся к какому-либо пара-

метру закона распределения вероятностей. Они

касаются,

обычно, знаков или рангов разностей

между последовательными значениями. Гипотеза

соответствует чисто случайному распределе-

нию.

Наиболее популярными непараметрическими

критериями

являются критерии Фишера, Уилкок-

сона,

ранговый критерий.

1.3.3.

Экспликативные детер-

министские

модели

1.3.3.1.

Схема разложения

временного

ряда

Y(l) - изучаемый ряд,

С(/) - тенденция,

S(Q - сезонная компонента,

е(0

- случайный член.

Аддитивная

схема:

представляет периодическое

явление с флуктуациями постоянной амплитуды:

Мультипликативная

схема: хорошо представля-

ет колебательное явление взрывного или затухаю-

щего

характера:

1.3.3.2. Методы оценки тенденции

1.3.3.2.1.

Метод скользящего среднего

Формируют

новый ряд z(tj, беря суммы взвешен-

ных последовательных значении

у{Т):

+*•

2(0=

/--*

ОБЩИЕ СВЕДЕНИЯ

Часто скользящие средние являются центриро-

ванными (к = к) и равновзвешенными

(

~&—Т~л

')-

Мвт

°Д

да

лишь

довольно фу-

быв оценки тенденции. Он полезен для сглажива-

ния кратковременных флуктуации.

1.3.3.2.2.

Метод

экспоненциального

сглаживания

Реализованные значения y(t) взвешиваются с

коэффициентами, составляющими геометричес-

кую прогрессию со знаменателем р:

2(0=

(1-

/-0

Параметр р* оценивается минимизацией суммы

квадратов остатков модели.

Обычно

р* = 0.7. Эта

модель может

быть

использована для

прогнозиро-

вания,

когда ряд хорошо укладывается вокруг го-

ризонтальной прямой.

1.3.3.3.

Связи

между

двумя

рядами

Когда

знание реализаций переменной X дает ин-

формацию о возможных значениях другой пере-

менной Y, говорят, что переменные X и Y связаны.

Обозначим

Е(У/х)

математическое ожидание Y при

условии,

что X принимает значение х; линия, со-

стоящая из точек (х,

E(Y(x)),

называется линией ре-

грессии.

Среди всех линий, сглаживающих облако

точек (х, у), она

является

наилучшей (обладает ми-

нимальной остаточной

дисперсией).

Если

линия ре-

грессии

- прямая, ее параметры оцениваются ме-

тодом наименьших квадратов:

Y = аХ + Ь,

где

а =

COV(X,

Ь =

Шу

—

ат

Использование линейной модели распространя-

ется на

случай

нескольких переменных X,,

,...,

X/;

именно:

Y =

... + а<Х,+ b

Замечание 1. Оценка а может

быть

определена

лишь в

случаях,

когда X

...

, X/ не связаны

линейной зависимостью.

Замечание 2. Введение дополнительных пере-

менных Х/+

... может сопровождаться уменьше-

нием

остаточной дисперсии, даже если эти новые

переменные в действительности не существенны

для объяснения поведения переменной Y.

Замечание 3. В

случае

линейной модели с не-

сколькими

переменными оценки а

смещены, если

реализации одной из переменных X, Х

;

авто-

коррелированы.

1.3.3.4.

Эконометрика

Эконометрическая модель служит для количе-

ственного

изучения соотношении, постулируемых

экономической

теорией.

Спецификация

состоит в

том,

чтобы

выразить те-

орию

в математической форме. Для этого использу-

ются эндогенные переменные, которые вводятся

при

моделировании, и экзогенные переменные, оп-

ределяемые вне моделирования. Часто дело сво-

дится к нескольким уравнениям при отсутствии од-

нозначного

разделения на объясняющие и объясня-

емые, результирующие переменные. В процессе

идентификации

анализируются соотношения меж-

ду решением (приведенной формой) модели и ее

спецификацией (структурной формой). Оценка па-

раметров производится методом наименьших квад-

ратов или двухшаговым методом наименьших квад-

ратов,

если обнаружены мешающие корреляции.

Иногда

эконометрические модели приводят к

рассмотрению

логарифмов переменных V, X, X*.

Коэффициенты а, а„ модели являются пока-

зателями упругости Y по отношению к каждой из

переменных X, X*:

v ** 3Y

- упругость Y по отношению к X*

1.3.4.

Стохастические модели

1.3.4.1.

Модель для одной

переменной

Имеется только один ряд Х(1).

1.3.4.1.1.

Стационарность

Ряд X(t) "стационарен", если:

Е(Х(0)-т

Var(X(i))

= о

СОУ(Х(0,Х(г+/7))

7(Л)|

же зависят от времени.

Примеры.

Белый

шум

e(t)

получается при

Е(е«)-0

VAR(e(l))

= о

COV(e(0,

e(f+n))

= 0

Vn#0.

2) Скользящее среднее MA(q) - это линейная

комбинация

белых

шумов

X(0 = e(Q-e,e(f-1)-...-e,e(f-<7)

3) Авторегрессия

Значения Х(1) - линейные комбинации значений

X(f- 1), X(f- 2) X(f- p). Процесс стационарен

для некоторых значений весовых коэффициентов.

4) Авторегрессия со скользящим средним

ARMA

()

Можно

показать, что всякий стационарный про-

цесс

записывается в форме

ARMA.