Басниев К.С. Энциклопедия газовой промышленности
Подождите немного. Документ загружается.

1 ОБЩИЕ СВЕДЕНИЯ
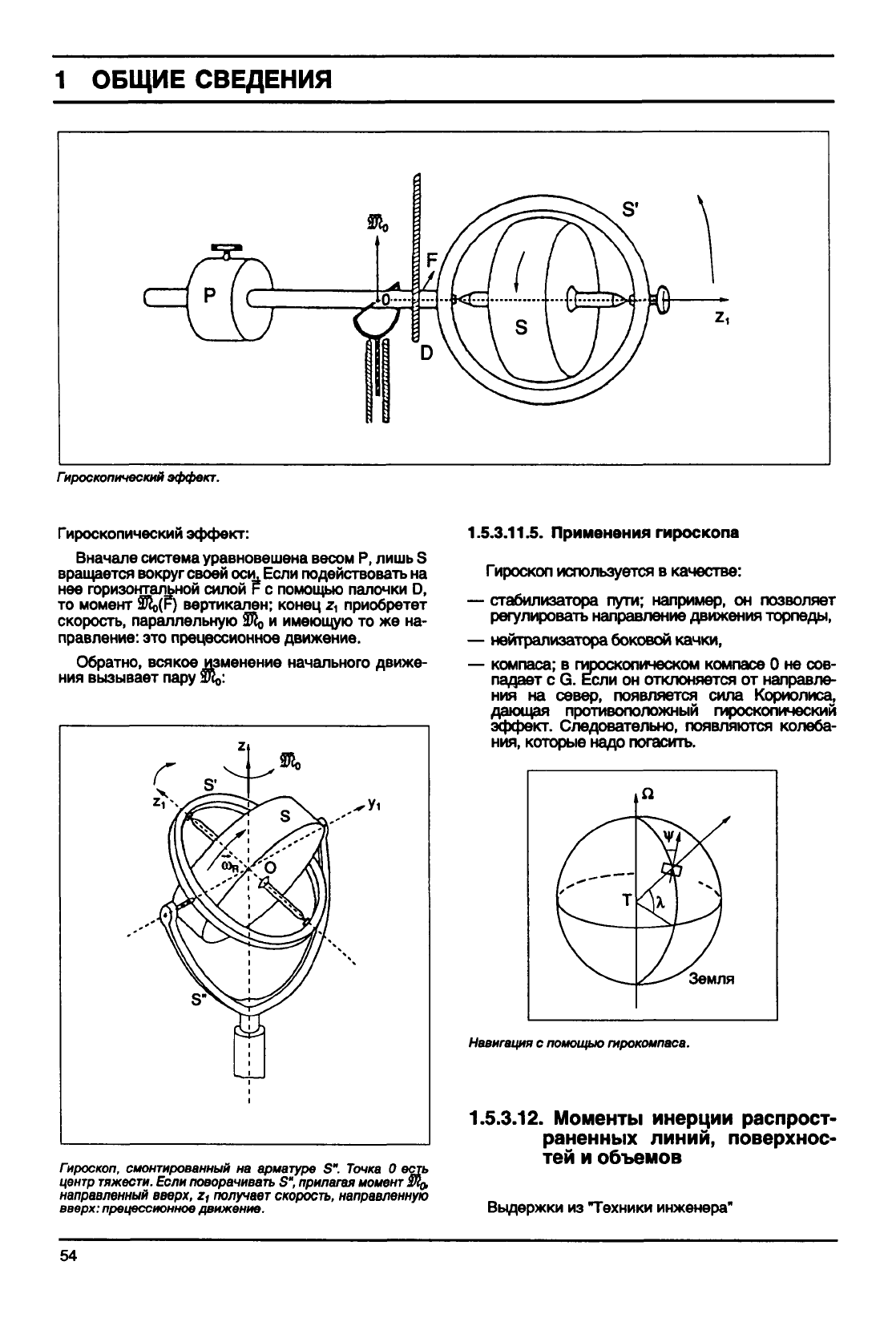
Гироскопический
эффект.
Гироскопический
эффект:
Вначале
система уравновешена весом Р, лишь S
вращается вокруг своей octi
Если
подействовать на
нее горизонтальной силой F с помощью палочки D,
то момент ЭДо(г) вертикален; конец z
1
приобретет
скорость,
параллельную
%> и имеющую то же на-
правление: это прецессионное движение.
Обратно, всякое
ния вызывает пару
5
энение начального движе-
Гироскоп,
смонтированный
на
арматуре
S". Точка 0
есть
центр
тяжести.
Если
поворачивать
S",
прилагая
момент
Silo,
направленный
вверх,
z
1
получает
скорость,
направленную
вверх:
прецессионное
движение.
1.5.3.11.5.
Применения гироскопа
Гироскоп
используется в качестве:
— стабилизатора пути; например, он позволяет
регулировать направление движения торпеды,
— нейтрализатора боковой качки,
— компаса; в гироскопическом компасе 0 не сов-
падает с G.
Если
он отклоняется от направле-
ния на север, появляется сила Кориолиса,
дающая противоположный гироскопический
эффект. Следовательно, появляются колеба-
ния,
которые надо погасить.
Ж
Навигация
с
помощью
гирокомпаса.
1.5.3.12.
Моменты инерции распрост-
раненных линий, поверхнос-
тей
и объемов
Выдержки из Техники инженера"
54
1 ОБЩИЕ СВЕДЕНИЯ
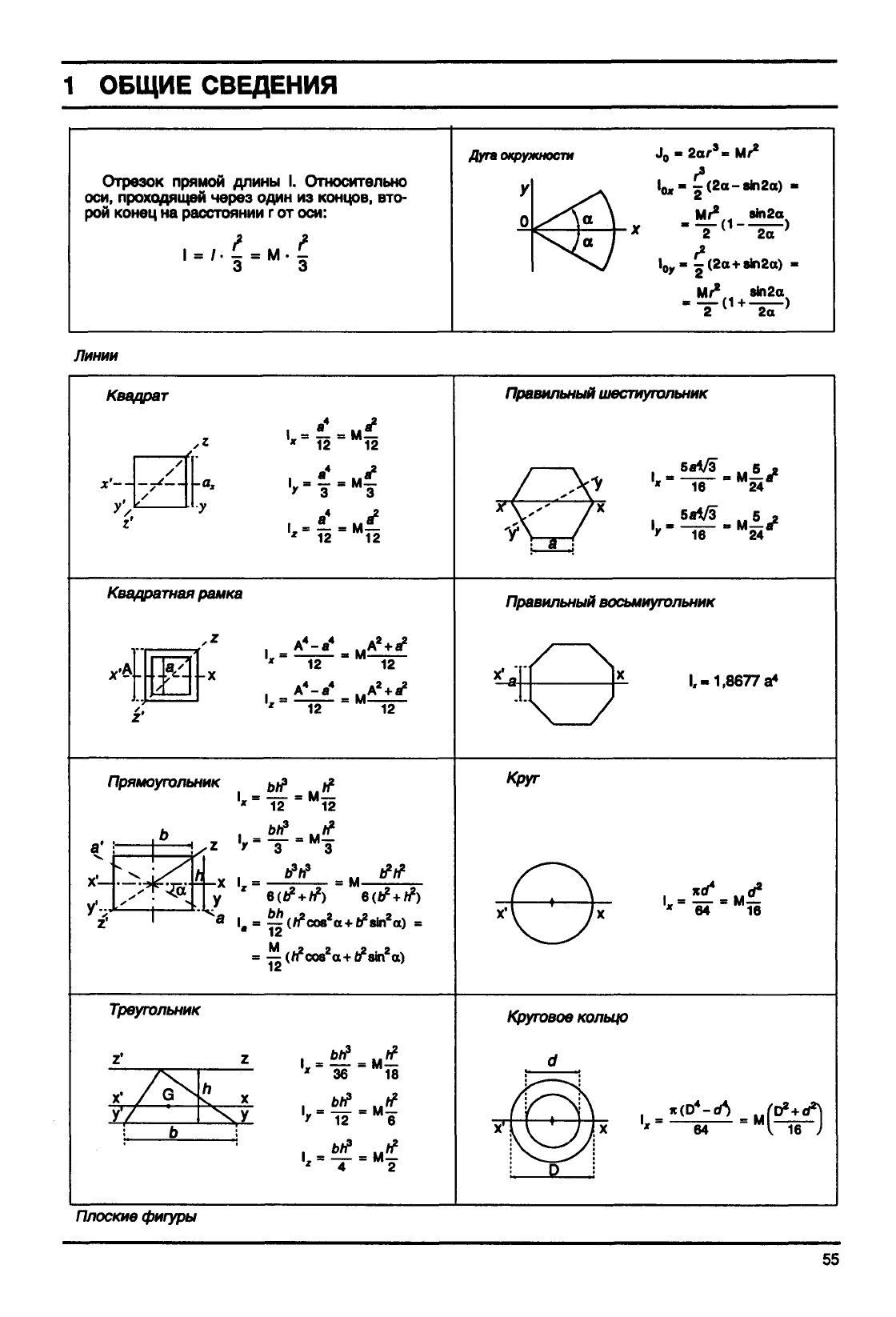
Отрезок
прямой
длины
I.
Относительно
оси,
проходящей через один
из
концов,
вто-
рой конец
на
расстоянии
г от оси:
Дуга
окружности
У
О
J
o
- 2<xr
s
« Mr
2
2
1
2а
•оу" 2
(2a+8in2<X)
Линии
Квадрат
у
*—I
1-V
'у з
12 "12
Правильный
шестиугольник
, 5aV3
Квадратная
райка
...V.
-х
12 12
Правильный
восьмиугольник
I,-1,8677
а
4
Прямоугольник
а;
х
1
-
*" 12
, _«?
V"
з
12
*?
3
=
м
/фуг
Треугольник
Z
1
х
1
/
У
1
/
Ь
z
V X
ЧУ
* ~ 36 18
M
12
~ "6
64
16
Плоские
фигуры
55
1 ОБЩИЕ СВЕДЕНИЯ
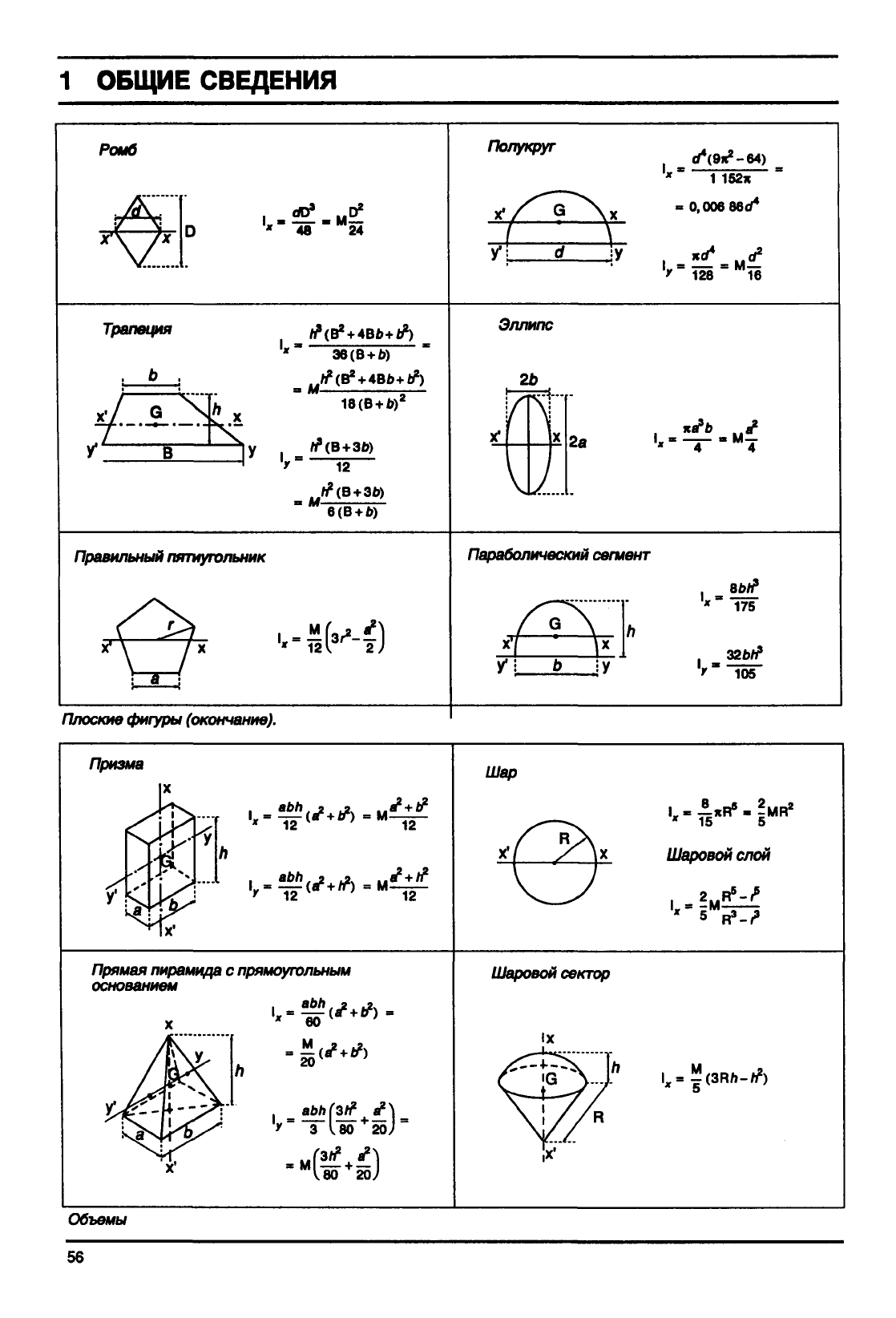
Ромб
jr\ 7*
48
24
Полукруг
(У
4
(9к
2
-64)
1 152*
0,008
86
d
4
Трапеция
Эллипс
Эв(В
+ Ь)
М-
В
У
12
=
м
2а
в(В + Ь)
Правильный
пятиугольник
Параболический
сегмент
i ь ;у
8W?
я=
*
175
*
Ш
2ЛЫ?
105
Плоские
фигуры
(окончание).
Призма
у
к.
(Ж-
Шар
Шаровой слой
Прямая пирамида
с
прямоугольным
основанием
Шаровой
сектор
20
_
abh(Zl?
'"^•1в0
Объемы
56
1 ОБЩИЕ СВЕДЕНИЯ
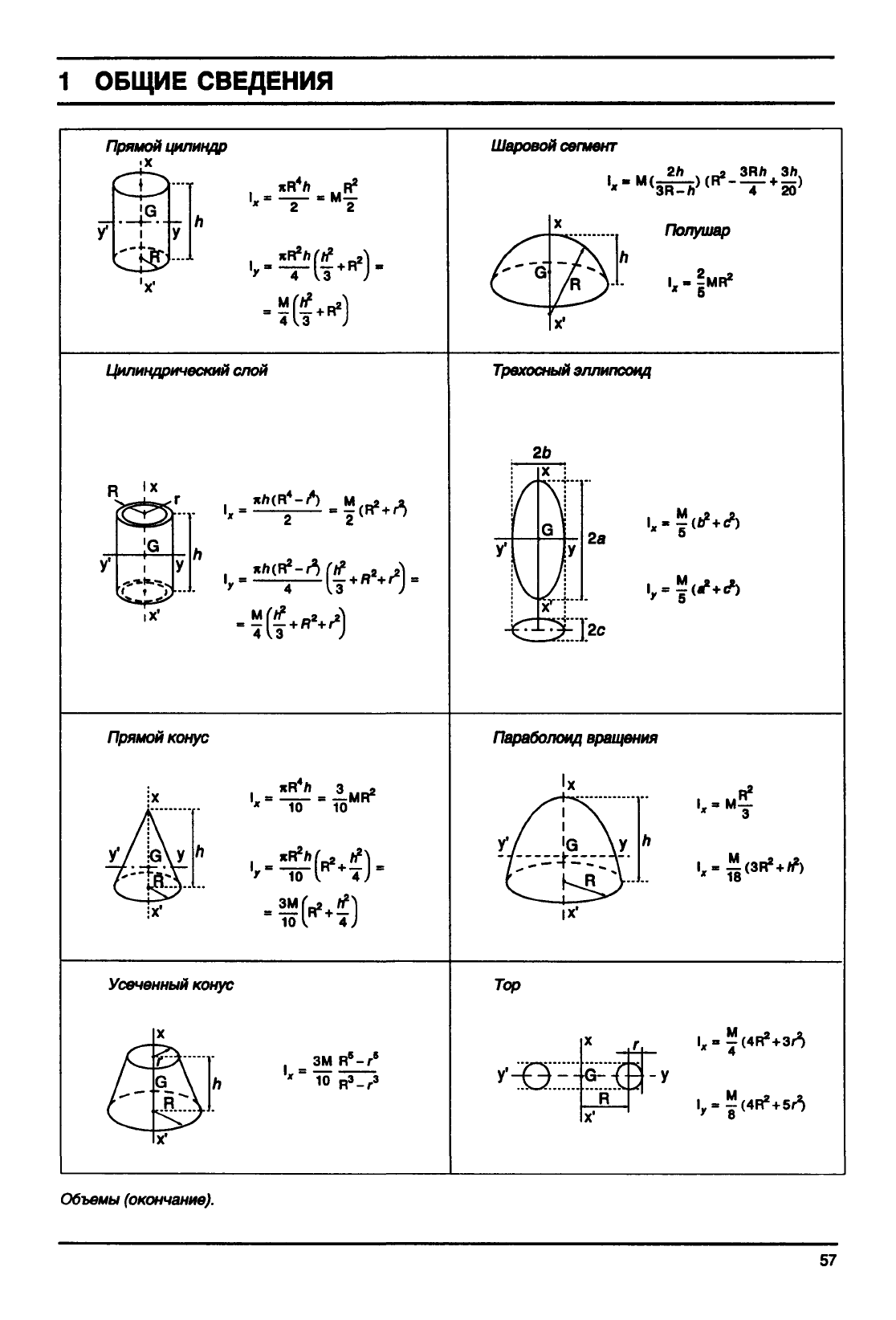
Прямой цилиндр
•
X
«В
4
/!
Г?
—-
М
Т
Шаровой
сегмент
Полушар
'.-I
м
"*
Цилиндрический
слой Трехосный эллипсоид
IX'
Прямой конус
Параболоид вращения
1х
L-
Н
Усеченный конус
Тор
_ ЗМ
R
8
-r
8
'"
Ю R
3
-r
3
-У
Объемы
(окончание).
57
1 ОБЩИЕ СВЕДЕНИЯ
1.5.4.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
Этот раздел касается
только
традиционных ма-
териалов, в частности металлов, но не термоплас-
тиков (см. разд.
1.5.5).
1.5.4.1.
Базовые эксперименты
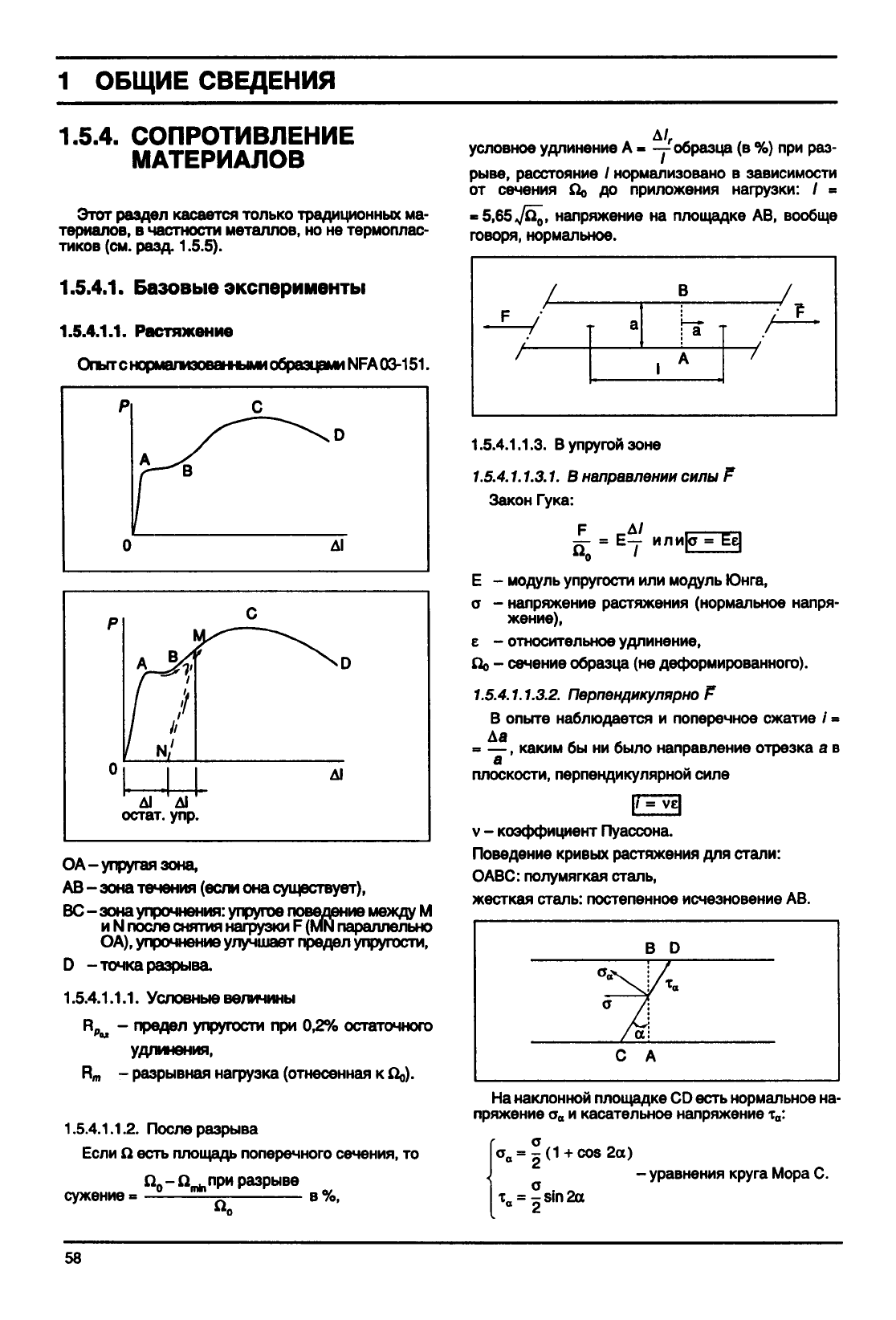
1.5.4.1.1.
Растяжение
Опыт
с нормализооаными образцами NFA
03-151.
р
0
(
I
п
Д1 Д1
эстат. упр
С
И^
^
Т ^\
\D
Д1
ОА - упругая зона,
АВ - зона течения (если она существует),
ВС - зона упрочнения: упругое поведение между М
и
N после снятия нагрузки F(MN параллельно
ОА), упрочнение улучшает предел упругости,
D
-точкаразрыва.
1.5.4.1.1.1.
Условные
величины
Rp^ - предел упругости при 0,2% остаточного
удлинения,
R
m
- разрывная нагрузка (отнесенная к До).
1.5.4.1.1.2.
После разрыва
Если Q есть площадь поперечного сечения, то
сужение
••
условное удлинение А - —'образца (в %) при раз-
рыве, расстояние / нормализовано в зависимости
от сечения По ДО приложения нагрузки: / =
-5,65
7^
>
напряжение на площадке АВ, вообще
говоря, нормальное.
/
в
/
F /
Г
а
1
|~а"
Т /
А '
1.5.4.1.1.3.
В упругой зоне
1.5.4.1.1.3.1.
В направлении
силы
F
Закон
Гука:
Е - модуль упругости или модуль Юнга,
о - напряжение растяжения (нормальное напря-
е
- относительное удлинение,
Оо - сечение образца (не деформированного).
1.5.4.1.1.3.2.
Перпендикулярно Р
В опыте наблюдается и поперечное сжатие / =
Да
Л
=
—, каким бы ни
было
направление отрезка а в
а
плоскости, перпендикулярной силе
v - коэффициент Пуассона.
Поведение
кривых
растяжения для стали:
ОАВС:
полумягкая сталь,
жесткая
сталь: постепенное исчезновение АВ.
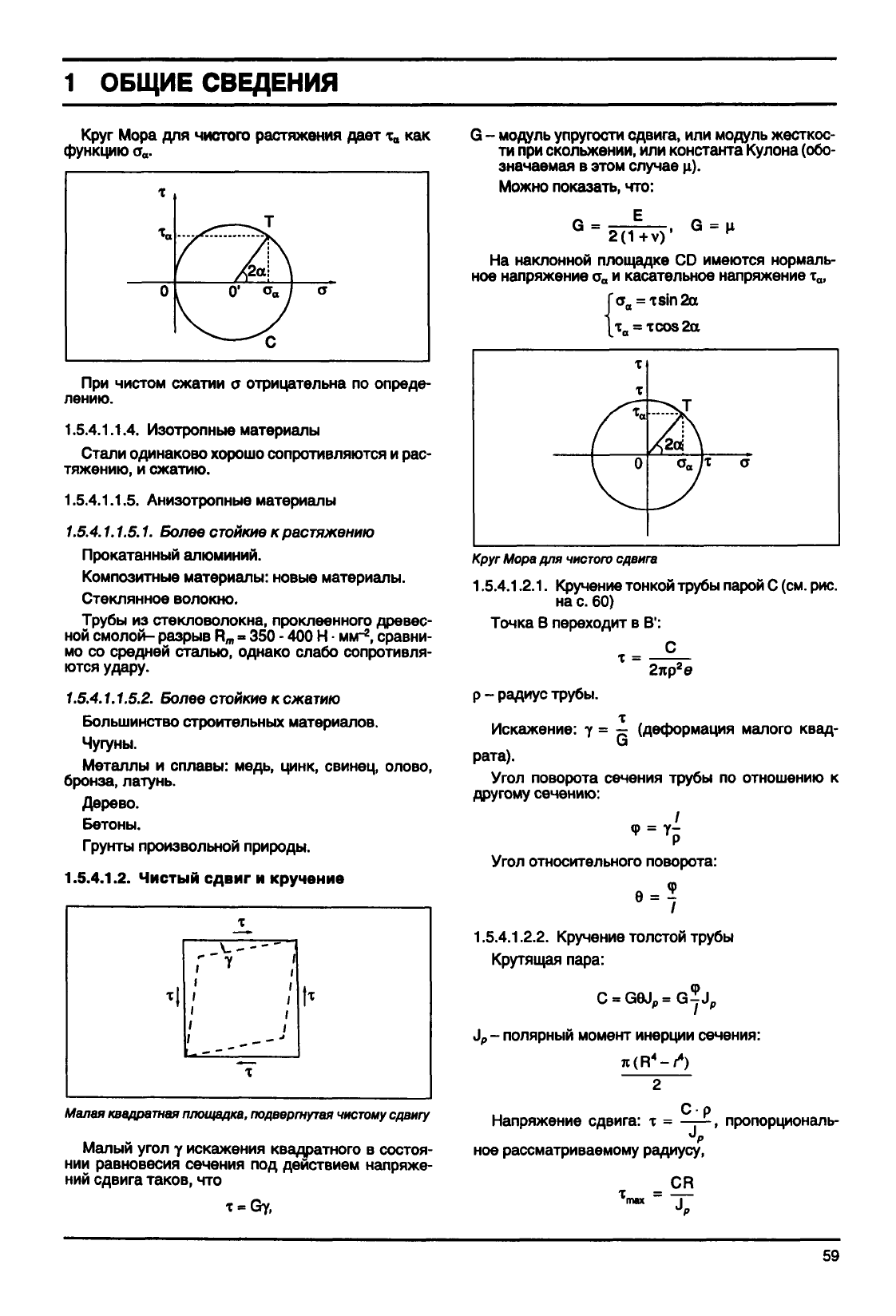
На наклонной площадке CD есть нормальное на-
пряжение о
а
и касательное напряжение v
|а.-|(1
t
= -sin2a
- уравнения круга Мора С.
58
1 ОБЩИЕ СВЕДЕНИЯ
Круг
Мора для чистого растяжения дает х
а
как
ФУНКЦИЮ
(Т
о
-
X
•
Т„
0
Г
При чистом сжатии а отрицательна по опреде-
лению.
1.5.4.1.1.4. Изотропные материалы
Стали
одинаково хорошо сопротивляются и рас-
тяжению, и сжатию.
1.5.4.1.1.5. Анизотропные материалы
1.5.4.1.1.5.1.
Болев
стойкие
к
растяжению
Прокатанный алюминий.
Композитные материалы: новые материалы.
Стеклянное волокно.
Трубы
из стекловолокна, проклеенного древес-
ной смолой- разрыв R
m
= 350 - 400 Н
•
мм-
2
, сравни-
мо со средней сталью, однако слабо сопротивля-
ются удару.
1.5.4.1.1.5.2.
Более
стойкие
к
сжатию
Большинство строительных материалов.
Чугуны.
Металлы
и сплавы: медь, цинк, свинец, олово,
бронза,
латунь.
Дерево.
Бетоны.
Грунты произвольной природы.
1.5.4.1.2.
Чистый сдвиг и кручение
Малая
квадратная
площадка,
подвергнутая
чистому
сдвигу
Малый угол у искажения квадратного в состоя-
нии равновесия сечения под действием напряже-
ний сдвига таков, что
G - модуль упругости сдвига, или модуль жесткос-
ти при скольжении, или константа Кулона (обо-
значаемая в этом
случае
ц).
Можно
показать, что:
~~2(1+v)'
На наклонной площадке CD имеются нормаль-
ное напряжение ст
а
и касательное напряжение х
а
,
, = xsin2a
х
а
= xcos 2а
X
I
°
/2сП
Круг Мора для
чистого
сдвига
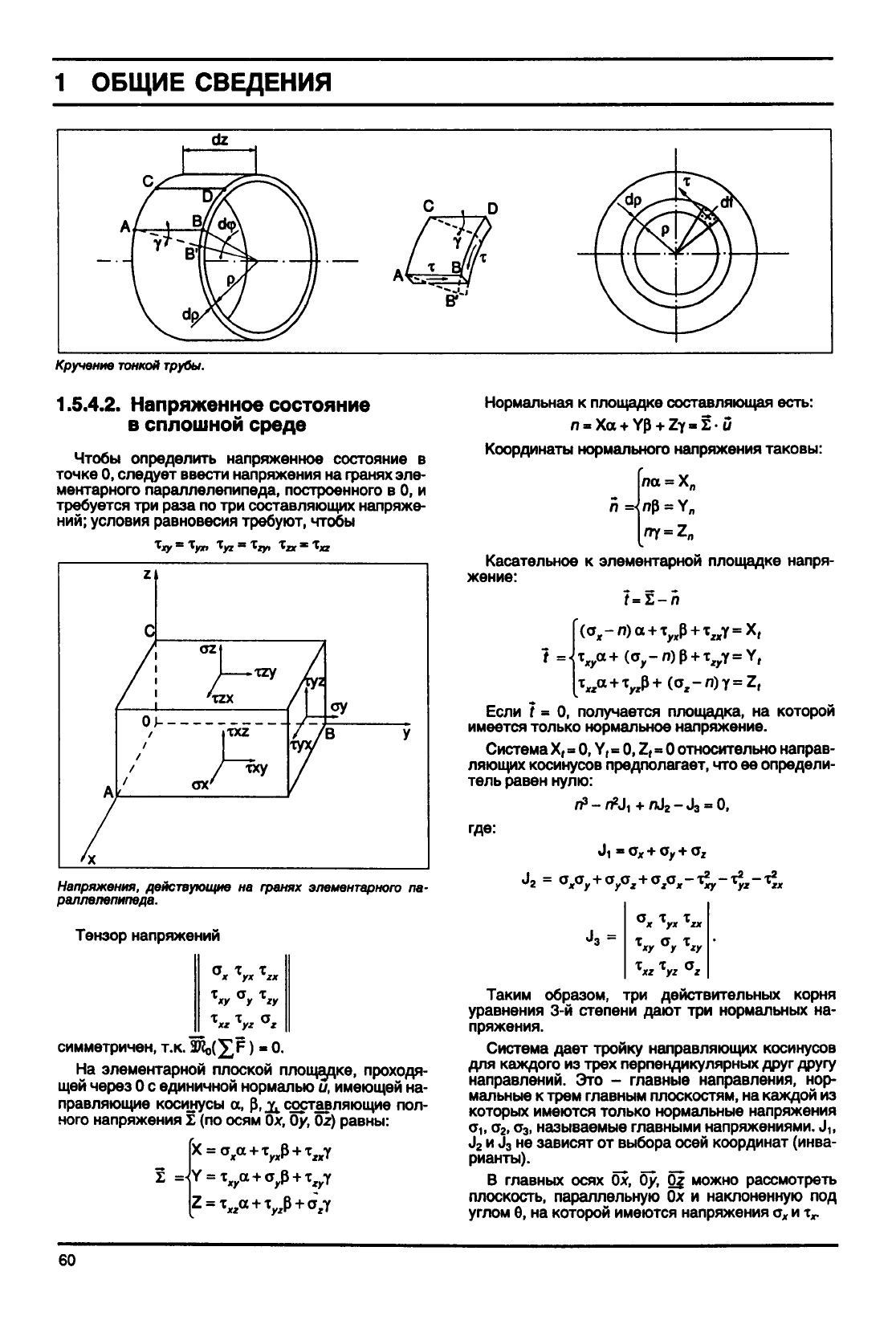
1.5.4.1.2.1.
Кручение тонкой трубы парой С
(см.
рис.
на с. 60)
Точка
В переходит в В':
х =
2яр
2
е
р
- радиус трубы.
Искажение: Y = р (деформация малого квад-
рата).
Угол
поворота сечения трубы по отношению к
другому сечению:
Угол
относительного поворота:
1.5.4.1.2.2. Кручение толстой трубы
Крутящая пара:
G?J
p
J
p
-
полярный момент инерции сечения:
Напряжение сдвига: х =
С-р
V
пропорциональ-
ное рассматриваемому радиусу,
CR
59
1 ОБЩИЕ СВЕДЕНИЯ
Кручение
тонкой
трубы.
1.5.4.2.
Напряженное состояние
в сплошной среде
Чтобы
определить напряженное состояние в
точке 0, следует ввести напряжения на гранях эле-
ментарного параллелепипеда, построенного в 0, и
требуется три раза по три составляющих напряже-
ний;
условия равновесия требуют,
чтобы
Напряжения,
действующие
на
гранях
элементарного
па-
раллелепипеда.
Тензор напряжений
т
*у
СТ
У
У*
симметричен,
т.к. 2Ro(^F) - 0.
На элементарной плоской площадке, проходя-
щей
через 0 с единичной нормалью
и,
имеющей на-
правляющие косинусы а, р,х составляющие пол-
ного напряжения £ (по осям Ox, Оу, 0z) равны:
Нормальная к площадке составляющая есть:
л-Xa + YP + Zy-f и
Координаты нормального напряжения таковы:
Касательное к элементарной площадке напря-
жение:
?=£-л
Если 7=0, получается площадка, на которой
имеется
только
нормальное напряжение.
Система Х,=
0,
Y,=
0,
Z,=0 относительно направ-
ляющих косинусов предполагает, что ее определи-
тель равен нулю:
n
3
-n
2
J
1
+ nJ
2
-J
3
= 0,
где:
* у у z z х ху yz
J.,=
У*
YZ
Таким образом, три действительных корня
уравнения 3-й степени дают три
нормальных
на-
пряжения.
Система дает тройку направляющих косинусов
для каждого из трех перпендикулярных друг другу
направлений. Это - главные направления, нор-
мальные к трем главным плоскостям, на каждой из
которых имеются
только
нормальные напряжения
<?i.
a
2
, °з> называемые главными напряжениями. J,,
J
2
и J
3
не зависят от
выбора
осей координат (инва-
рианты).
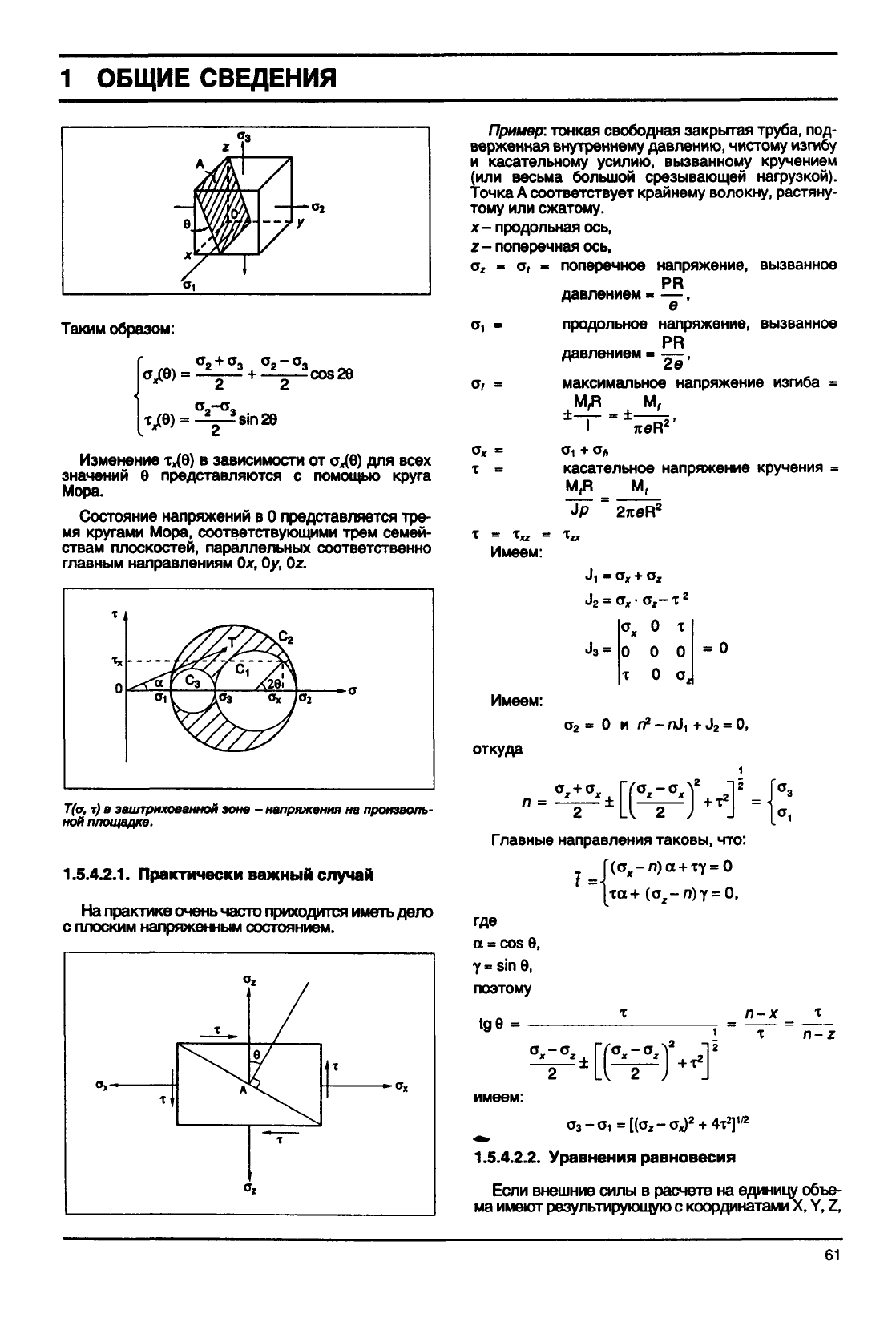
В
главных
осях Ох, б/, б| можно рассмотреть
плоскость, параллельную Ох и наклоненную под
углом 6, на которой имеются напряжения о
х
и т
г
60
1
ОБЩИЕ СВЕДЕНИЯ
в.
Ж
7
у
Таким образом:
°2 ~
С
3
Изменение т*(8) в зависимости от аДв) для всех
значений 6 представляются с помощью круга
Мора.
Состояние напряжений в 0 представляется тре-
мя кругами Мора, соответствующими трем семей-
ствам плоскостей,
параллельных
соответственно
главным направлениям Ox, Oy, Oz.
Т(а,
х) в
заштрихованной
зоне -
напряжения
на
произволь-
ной
площадке.
1.5.4.2.1.
Практически важный случай
На практике очень часто приходится иметь
дело
с плоским напряженным состоянием.
Пример:
тонкая свободная закрытая труба, под-
верженная внутреннему давлению, чистому изгибу
и
касательному усилию, вызванному кручением
(или весьма большой срезывающей нагрузкой).
Точка
А соответствует крайнему волокну, растяну-
тому или сжатому,
х- продольная ось,
z- поперечная ось,
а
г
ж a, ~ поперечное напряжение, вызванное
PR
давлением - —,
0
о, = продольное напряжение, вызванное
PR
давлением = -^,
а,
максимальное напряжение изгиба
касательное напряжение кручения
M,R М,
Имеем:
J
2
= а
х
•
а
г
- т
2
г
°
Т
0
0 0
т 0 о,
=
0
Имеем:
откуда
а
г
= 0 и л
2
- nJ, + J
2
= 0,
Главные
направления таковы, что:
Г(а-п)а + ту = О
f
=••
где
а = cos 9,
у = sin 6,
поэтому
tge
= —
п-х
cf.-a,
n-z
имеем:
1.5.4.2.2.
Уравнения равновесия
Если
внешние силы в расчете на единицу объе-
ма имеют результирующую с координатами X, Y, Z,
61
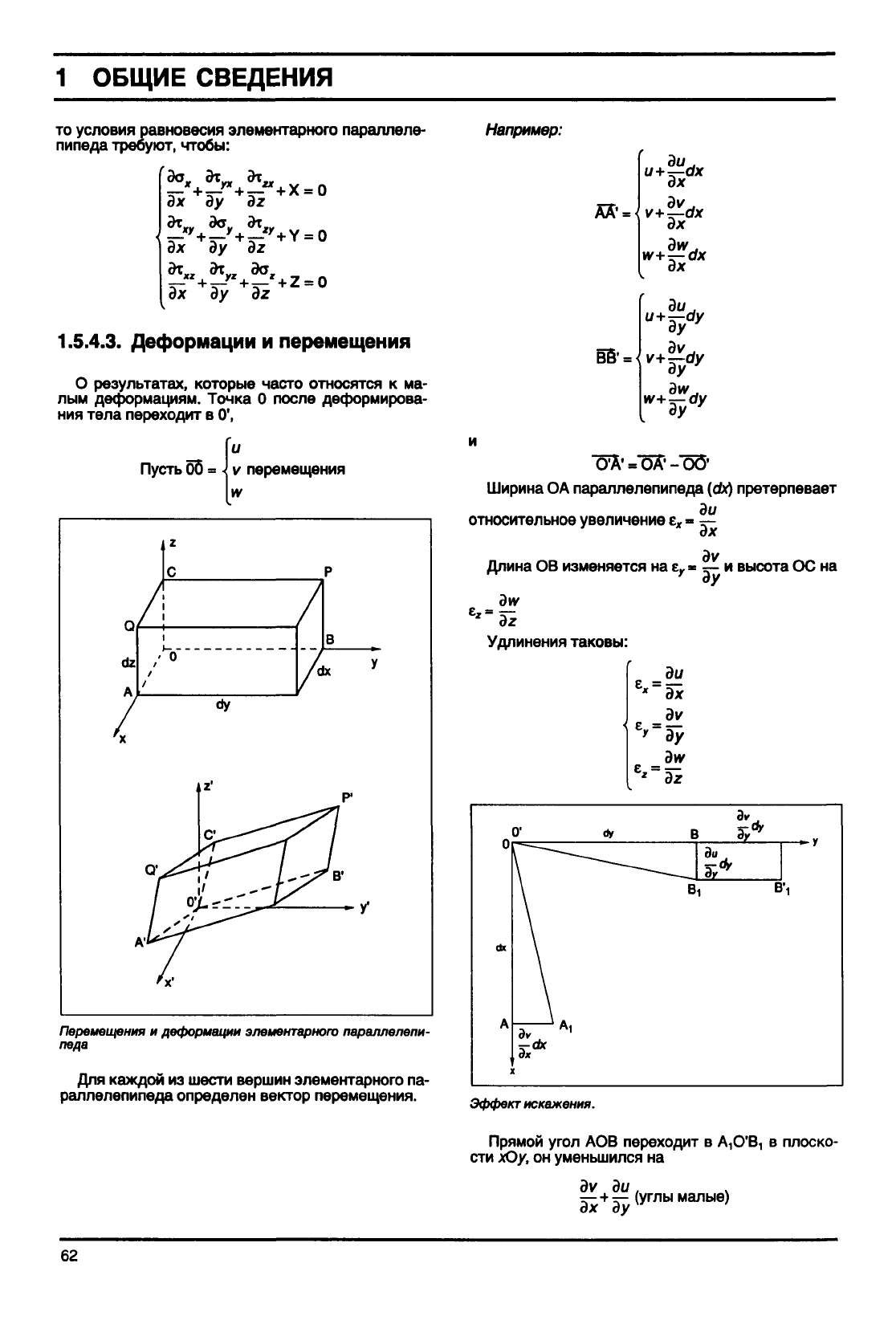
1 ОБЩИЕ СВЕДЕНИЯ
то
условия
равновесия элементарного параллеле-
пипеда требуют,
чтобы:
Например:
do
x
Эх
Эх
by dz
x
Эх &*ix
*т*
_ т Л — U
d
Эх
ду dz
++
-
Эх
ду dz
1.5.4.3.
Деформации
и
перемещения
О результатах, которые часто относятся
к ма-
лым деформациям. Точка
0
после деформирова-
ния тела переходит
в О',
Пусть
65 =
J.
v
перемещения
\w
Q
dz
А
1
1
А
/-о~~~
.
dy
Z
1
CV^—*^\s
'
/•"
'х
1
Р
7
В
т
г
Перемещения
и
деформации
элементарного
параллелепи-
педа
Для каждой
из
шести вершин элементарного
па-
раллелепипеда определен вектор перемещения.
du.
U+
dx
d
*
^d
Эх
dw
Эх
dw
zr-d
ду
Ширина
ОА
параллелепипеда (dx) претерпевает
ди
относительное увеличение
е
х
- ^~
Длина
ОВ
изменяется
на е
г
- ^- и
высота
ОС на
Удлинения таковы:
Эй
Эх
dv
dy
dw
0
dx
А
О
1
_
\
\
J
Ai
dy
~^
В
-—-^
В
1 °
^У
t
Эффект
искажения.
Прямой угол
АОВ
переходит
в
А,О'В,
в
плоско-
сти
хОу, он
уменьшился
на
dv
du . .
^-
+ я-
(углы
малые)
Эх
Эу
62

1 ОБЩИЕ СВЕДЕНИЯ
Искажения определены величинами:
Эх
Эу
ди
QQ
1
=
Эх bz
dw. 3w.
w+ — dx+ — dz
Эх dz
Можно показать, что деформации образуют
симметричный тензор:
1 1
Y
е
х
1
1
2'
XJ
2
Тс*
, «V
1
• 2 У*
2'*х
1
и что существуют три
главных
направления: три
плоскости,
в которых нет искажений.
1.5.4.4.
Связи между напряжениями
и
деформациями
в сопротивлении материалов
1.5.4.4.1.
Упругость (упругие
тела):
обобщен-
ный закон Гука
1.5.4.4.1.1.
Изотропные материалы
Искажения:
поскольку нормальные напряжения вызывают уд-
линения,
параллельные
их направлениям, и суже-
ния в
двух
перпендикулярных направлениях.
Кубическое расширение:
1.5.4.4.1.2. Другая точка зрения
Коэффициенты Ламе X и ц определяются равен-
ствами:
значит
Ev
2(1
1.5.4.4.2.
Термический эффект
=
G
К
относительным удлинениям, вызванным на-
пряжениями, следует добавить удлинения,
вызванные увеличением температуры, например,
е
т
= <х
т
ДТ, а
т
- коэффициент удлинения.
Замечание:
Если
помешать удлинению, возникает напряже-
ние сжатия:
Поэтому имеем:
1 ,
е
/
=
Ё
т
=
-Еа
т
ЛТ.
г
-у(о
у
+ст
г
)
= - [а
г
-v
+
с
у
)
]
1.5.4.5.
Закон предельных состояний
материала
Удлинения:
уг _ zx
"G
'
Y
" " СГ
Приводит:
либо к упругому пределу,
либо к разрыву.
Теория предельных состояний Мора-Како в на-
стоящее время признана всеми.
1.5.4.5.1.
Предел на разрыв
Зная в точке М образца три
главных
напряже-
ния,
нарисуем самый большой круг Мора.
Если
он
касается кривой, называемой огибающей Како на
разрыв, в этой точке М реализуется разрыв.
63
