Басниев К.С. Энциклопедия газовой промышленности

Подождите немного. Документ загружается.

1 ОБЩИЕ СВЕДЕНИЯ

1.5.3.6.

Удар двух тел

1.5.3.6.1.

Импульс силы

Пусть P(Q - контактная сила, с которой тело В

действует на тело А, другие силы пренебрежимы.

?(t)dt

- Р - импульс силы.

rlMOOM

6Д л (7, -7,)

J, (й\ -Й,).

1.5.3.6.2.

Абсолютно неупругий удар

Оба

тела

остаются соединенными вместе после

удара. Сохраняются: количество движения

m,v, + m

л 7

- момент инерции совокупности двух тел по от-

ношению к ее центру тяжести.

Не сохраняется кинетическая энергия:

(лт, +

кинетический

момент

Если

нет вращения, потеря кинетической энер-

гии

равна

Она переходит в тепло.

Пример:

свинцовая

пуля

расплющивается о сте-

ну (/Пг = о», v

= 0). Энергия пули -т

v? теряется и

превращается в тепло.

Пуля

плавится.

1.5.3.6.3.

Абсолютно упругий удар

Р производит работу по деформированию А,

равную потенциальной

энергии,

которая восста-

навливается из кинетической

энергии:

т,К

- v?) +

- ф + J, (П

•*

-12^) +

М,

Даже при неупругом

столкновении

количество

дви-

жения должно

сохраняться.

Рассмотрим

столкнове-

ние,

котором

частицы

остаются

соединенными.

До удара

f=0

t>0

После удара:

или

v =

Ц. М.

f<0

'к

В системе отсчета центра масс, скорости

и М,до

столкновения

-это

и?

После столкновения (Mf

Мг) находится

покое.

1.5.3.6.3.1.

Удар

двух частиц или "фронтальный"

УДар

Имеем:

откуда

ОБЩИЕ

СВЕДЕНИЯ

1.5.3.6.3.2.

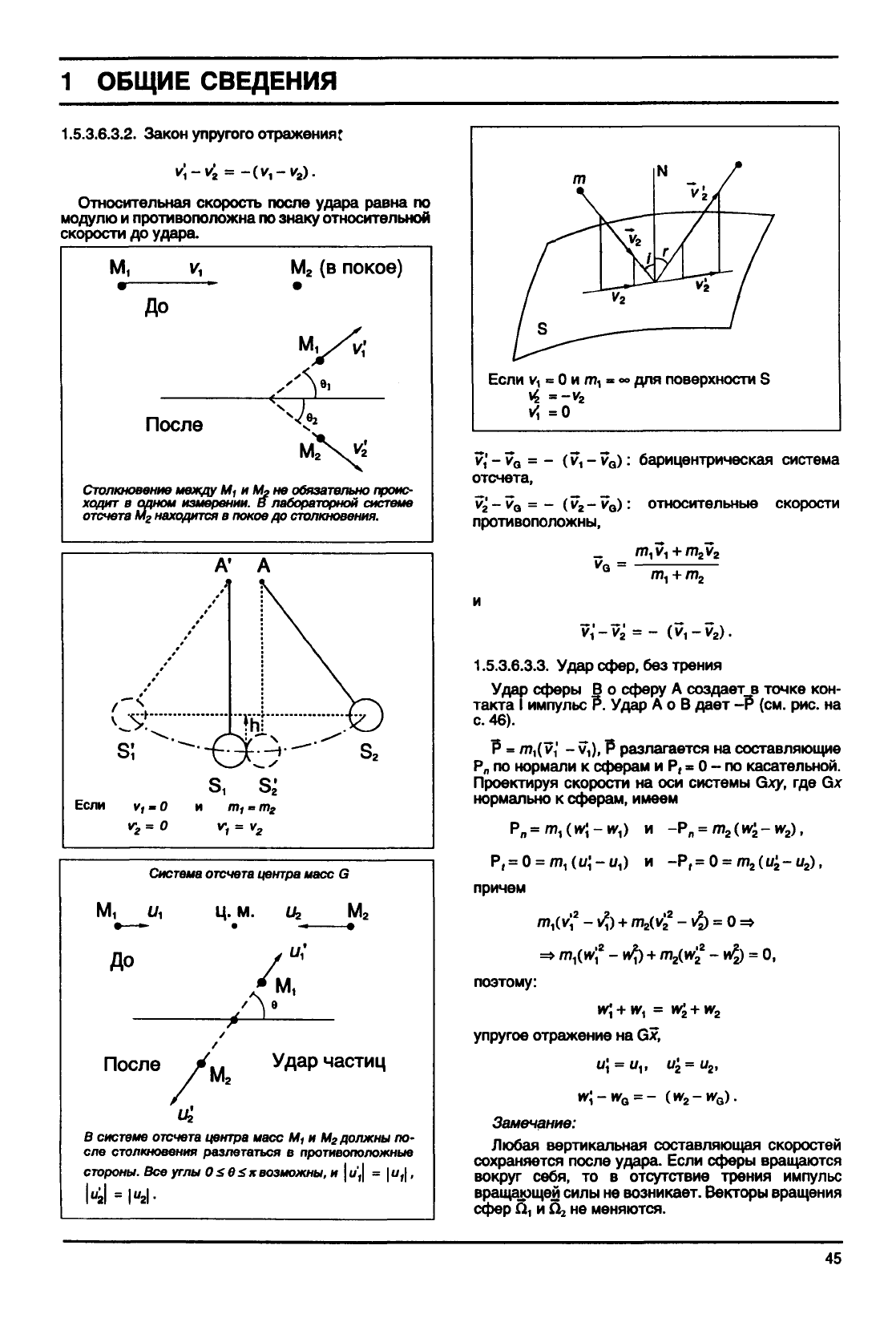
Закон упругого отражения:

Относительная скорость после удара равна по

модулю и противоположна по знаку относительной

скорости до удара.

(в

покое)

До

После

Столкновение

между

М, и М, не

обязательно

проис-

ходит

одном

измерении,

лабораторной

системе

отсчета

находится

покое

до

столкновения.

Система

отсчета

центра

масс

М, U, Ц. М. Uz М

До

* м.

После

Удар частиц

системе

отсчета

центра

масс

М, и М

должны

по-

сле

столкновения

разлетаться

противоположные

стороны.

Все

углы

0 £ в £ я

возможны,

и\\ =

Г.

^--

Если

v, = 0 и m,

^ =-v

v? =0

(

= оо для

поверхности

^'-VQ

= - (v

-v

): барицентрическая система

отсчета,

'-v

= -

-и

относительные скорости

противоположны,

1.5.3.6.3.3.

Удар сфер, без трения

Удар

сферы

В о сферу А создает в точке кон-

такта

импульс

Р. Удар А о В дает -Р (см. рис. на

с. 46).

Р =

/77,(7,

- v,), P разлагается на составляющие

по нормали к сферам и Р, = 0 - по касательной.

Проектируя скорости на оси системы Gxy, где Gx

нормально к сферам,

имеем

(w;-n'

) и -Р

-ид,

и -P

=0 =

-u

причем

- ф = 0 =>

поэтому:

упругое отражение на Gx,

Замечание:

Любая вертикальная составляющая скоростей

сохраняется после удара. Если

сферы

вращаются

вокруг себя, то в отсутствие трения

импульс

вращающей

силы

не возникает. Векторы вращения

сфер ft, и Йг не меняются.

1 ОБЩИЕ СВЕДЕНИЯ

( А, ]

р,

х|

Рп

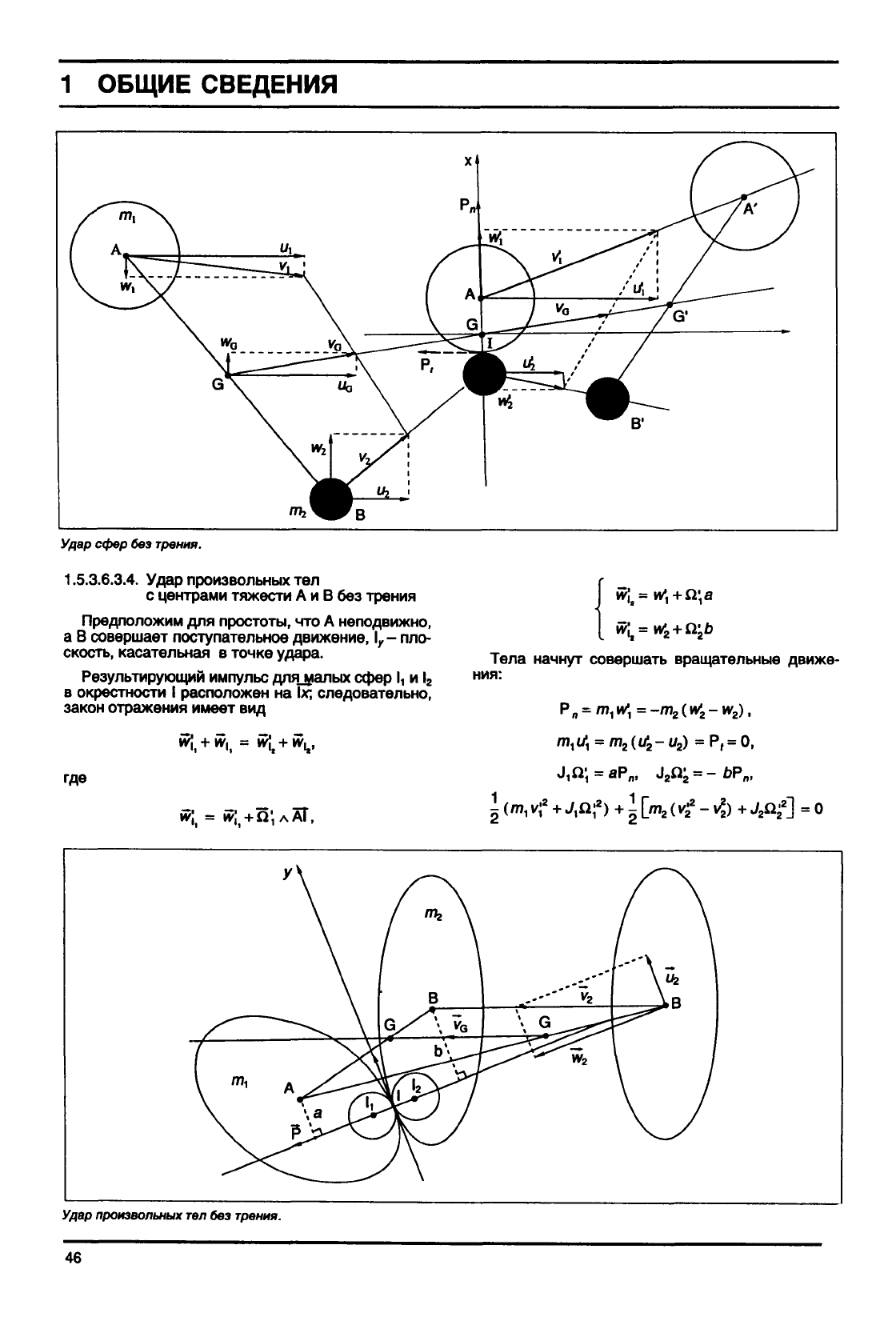
Удар

сфер

без

трения.

1.5.3.6.3.4.

Удар

произвольных

тел

с центрами тяжести

А и В без

трения

Предположим

для

простоты,

что А

неподвижно,

совершает поступательное движение,

- пло-

скость, касательная

точке удара.

Результирующий импульс для_малых сфер

I, и l

в окрестности

расположен

на

\х, следовательно,

закон

отражения имеет

вид

где

Тела начнут совершать вращательные движе-

ния:

07,1/;

= m

- и

)

=Р,

= 0,

J,a\ = aP

, J

«'=-bP

(m,

+ J,

д;

) +1

[/n

(v,

- ^)

.У

]

Удар

произвольных

тел без трения.

1 ОБЩИЕ СВЕДЕНИЯ

1.5.3.6.4.

Реальные удары

1.5.3.6.4.1.

Энергия деформации не полностью

восстанавливается за время

-t

Частичное отражение, коэффициент восстанов-

ления г\:

1.5.3.6.4.2. Касательный импульс есть

Р.

Р/, если — s tg ф,

- угол трения,

" Р

Р/= P

Ф,

как только ^ =

• п

1.5.3.7.

Осцилляторы

Примеры:

— масса, подвешенная на пружине,

период:

То = 2ж№.

к -жесткость пружины (элементарный коэффи-

циент удлинения, деленный на элементарную си-

лу);

— крутильный маятник: тело вращения, подве-

шенное на упругой нити: Т

= 2я /—,

С - постоянная кручения (отношение элемен-

тарного

угла к элементарной паре);

— физический маятник массы М:

• малые колебания:

Т„ = 2я.

'"""'WM^i

большие колебания:

OG,

— математический маятник (материальная точка,

подвешенная на нити):

1.5.3.7.1.

Осциллятор с вязким трением

Пример:

масса, подвешенная на пружине с гид-

равлическим амортизатором t

F?+kx=

Обозначим:

тогда:

где

. dx

х = — и

- —

©о

- циклическая частота осциллятора или собст-

венная циклическая частота, Т

- собственный пе-

риод,

- собственная частота,

К,

= коэффи-

циент затухания (в с~'), х=0- положение равнове-

сия.

—

псевдопериодический

режим:

х = Ae^'cos (wf + ф),

затухающие колебания около положения равнове-

сия:

псевдопериод:

Тк

(Уф

-sin

—sin

1/2 •

средние

колебания:

для а = - имеем "Г

= 1,23 Т„

X а

]

дляГ=О:

х = Хо©"*' (cos wt + — sin wO

Затухающее

колебательное

движение

1 ОБЩИЕ

СВЕДЕНИЯ

— критический режим:

;•-«£«

о. e

- (At + В) в"™

' - апериодическое движение.

Этот

случай

важен для амортизации колебаний в

измерительных приборах;

при

Г-О

И V

= О: х =

(—+

'о

в момент t = Т

х= 0,0136хь-О,

т.е.

близко к положению равновесия:

0.75-

0.50-

0.25-

*о

0.25

0.50 0.75

т =

— апериодический режим:

решение вида

"возвращение" в положение равновесия более дли-

тельно.

1.5.3.7.2.

Вынужденные колебания

F cos at,

х+2£х+а>

х = — cos cof.

Затухающие колебания со временем исчезают,

после чего остается:

А =

x = Acos(cof+9),

F 1

.1/2

ш -to,

Если

С,

О,5?о,

An», =

,15AQ

(AQ

при

ее

= 0),

получает-

ся амортизация автомобилей:

Со =

О =

г'

если ^ < ^о (С мало), имеется резонансный пик амп-

литуды:

А о

или — = —.

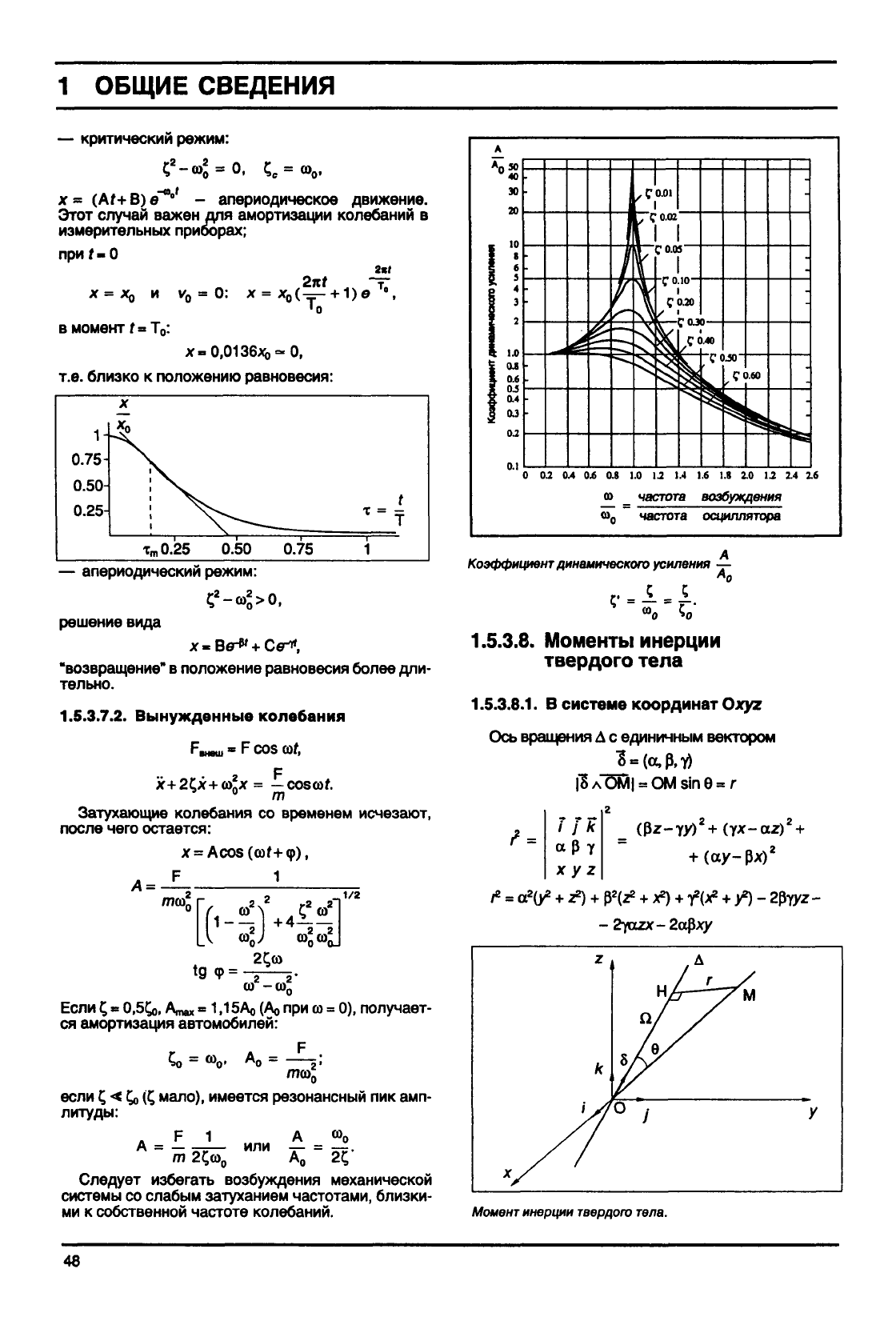
Следует

избегать возбуждения механической

системы

со слабым затуханием частотами, близки-

ми

к собственной частоте колебаний.

1.0

0.6

0.5

0.4

0.1

•

Г/

—•*,

--*

0.01

0.02

С 0.0S

С 0.20

/ i

(,'OJO

о.бо

•

О 02 0А 0.6 0.8 1.0 12 1.4 1.6 1.8 10 1.2 2.4 2.6

с»

частота

возбуждения

о>

частота

осциллятора

Коэффициент

динамического

усиления —

1.5.3.8.

Моменты инерции

твердого тела

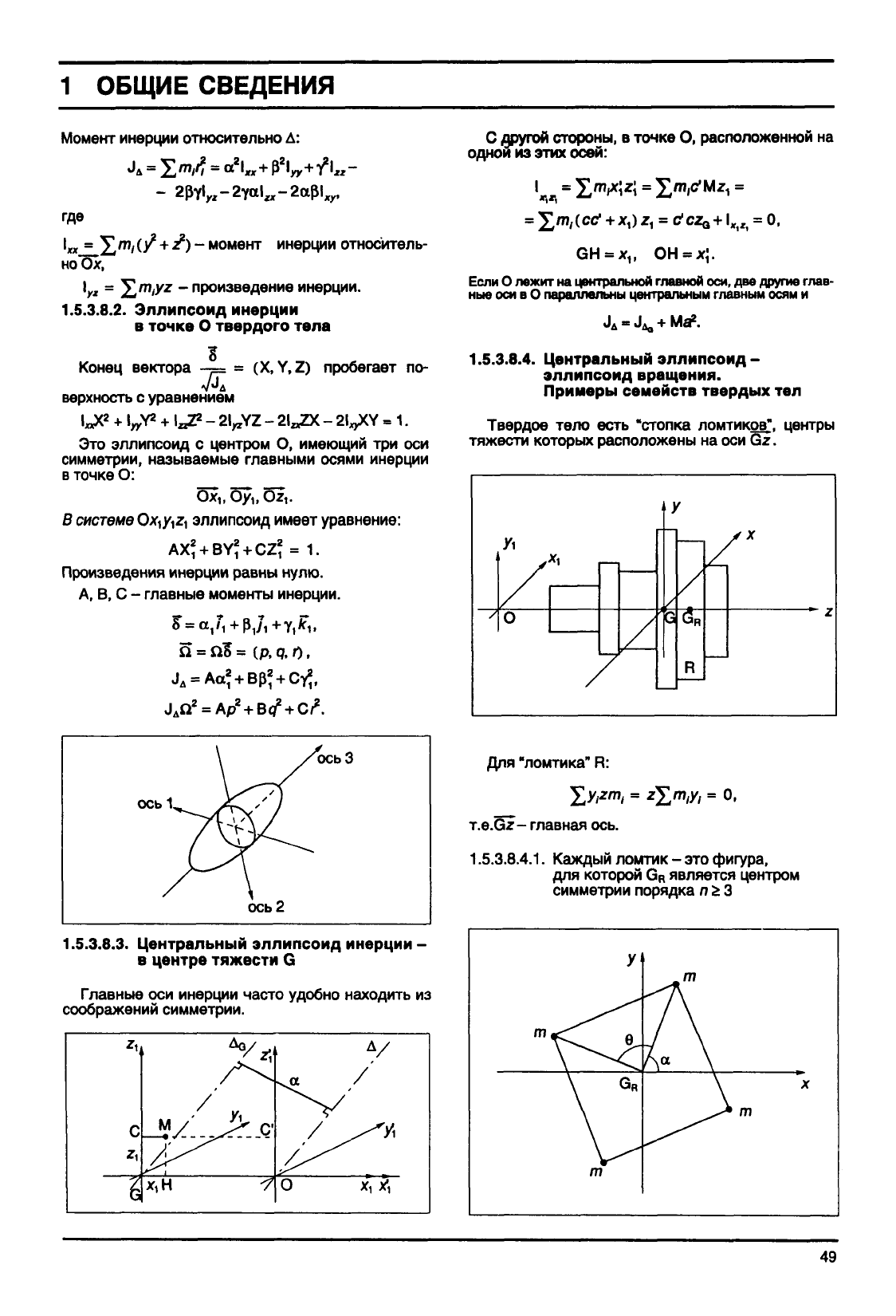
1.5.3.8.1.

системе

координат

Oxyz

Ось вращения А с единичным вектором

(ссу-рх)'

у z

) +

(z2

+ х

) +

fix

+ у

) -

2Pyyz-

-2yoczx-2apxy

Момент

инерции

твердого тела.

ОБЩИЕ СВЕДЕНИЯ

Момент инерции относительно А:

где

_=_£

т, (у

+ z

) - момент инерции относитель-

но Ох,

уж

= ^m,yz - произведение инерции.

1.5.3.8.2.

Эллипсоид инерции

в точке О твердого тела

Конец вектора -= = (X, Y, Z) пробегает по-

верхность с уравнением

I**

+ \„Ч* + \J?-

ZXyzYL

2I«ZX

- /

Это эллипсоид с центром О, имеющий три оси

симметрии,

называемые главными осями инерции

в точке О:

бх,, Оу

57,.

системе

Ох^г, эллипсоид имеет уравнение:

+ BY

Произведения инерции равны нулю.

А, В, С - главные моменты инерции.

(р, qf, i),

1.5.3.8.3.

Центральный эллипсоид инерции -

в центре тяжести G

Главные

оси инерции часто удобно находить из

соображений симметрии.

x,H 7

0 х

, х

С другой стороны, в точке О, расположенной на

одной из этих

осей:

ДСС

+ X,) Z, = C*CZQ + I

X)Z)

= О,

Если О лежит на центральной главной оси, две другие глав-

ные оси в О параллельны центральным главным осям и

1.5.3.8.4.

Центральный эллипсоид-

эллипсоид вращения.

Примеры семейств твердых тел

Твердое

тело

есть 'стопка ломтиков^, центры

тяжести которых расположены на оси Gz.

У1

1—1

* Z

Для "ломтика" R:

О,

T.e.Gz-

главная ось.

1.5.3.8.4.1.

Каждый ломтик - это фигура,

для которой G

является

центром

симметрии

порядка л 2:3

\ G

\ *

^^ т

1 ОБЩИЕ СВЕДЕНИЯ

Ломтик

- совокупность материальных точек, рас-

положенных в вершинах правильного многоуголь-

ника

с в = —:

*-0

п-1

8ln

(o+

/№),

«г-0

л-1

*-0

при любой ориентации a.

n-1..

=0.

*-o

Зубчатая

передача.

Турбина.

1.5.3.8.4.2.

Каждый ломтик - это один

или несколько витков винта

Данному

/соответствует один х> 0 и один х< 0.

-0.

Точно

так же в

только

момент инерции С выде-

ляется,

А = В. Частный случай - тело вращения.

Червячная

передача с двойной нарезкой.

1.5.3.9.

Движение твердого тела

одной неподвижной

точкой О. Общие уравнения

1.5.3.9.1.

Кинетический момент

относительно О

Система отсчета, составленная главными осями

инерции,

есть

Ох,/^,.

Тогда

= Л л ОМ =

I IF,

q r

*i /i г,

где

. (qz, - лк)£ + (/x, -

pzjjy

+ (py, -

= (U,, V,, W,),

ОМ

л v

7, 5

Кинетический

момент:

= £трм л 7

= Арл, + Bq/, + Cr£,,

поскольку произведения инерции, такие как

J^m^z,

равны

нулю.

Замечание:

Точка О может

быть

центром тяжести.

Движение

твердого

тела

с неподвижной

точкой

О.

1 ОБЩИЕ

СВЕДЕНИЯ

1.5.3.9.2.

Теорема

кинетическом моменте

••

АрГ, +

B<j/,

I IF

q r

Bq Сл

Уравнения Эйлера:

Ap+(C-B)qr=2R

Bg+

(А-С) rp

2JJ

•

М,

1.5.3.9.3.

Кинетическая энергия

1.5.3.10. Свободное движение

или движение Пуансо

Случай,

котором ЗЙ^Рвнеш)

внешние силы

проходят через

О.

Замечание:

О может

быть

центром тяжести: свободное

вращение

тела

вокруг центра тяжести.

Тогда:

<?о

const

-ll

const.

1.5.3.10.1.

Тело, приведенное

во

вращение

вокруг главной

оси

инерции

= д =

0иг= const: вращение продолжается

равномерно (вокруг главной оси

0z).

Вес

уравновешивает систему

состоянии

по-

коя.

Когда

приведено

во

вращение, последнее

продолжается бесконечно долго

при

отсутствии

трения.

Тем

не

менее, вращение вокруг средней главной

оси

инерции неустойчиво.

1.5.3.10.2.

Тело, приведенное

во

вращение

вокруг произвольной

оси

постоянный вектор,

= -Й

•

постоянно, следовательно,

ОН -

- const.

q, г)

протыкает эллипсоид

i =

P Я г

нормаль

эллипсоиду имеет направляющий

вектор

п=

он

параллелен

Наконец:

.а

Ар

const,

откуда

const.

Плоскость

Р,

касательная

эллипсоиду

точке

постоянная. Мгновенная скорость

точке плоско-

сти,

лежащей

на

эллипсоиде, равна

нулю

лежит

на мгновенной

оси

вращения

А).

Движение твердого

тела

таково,

что

эллипсоид

инерции

точке

вращается

катится

без

сколь-

жения

по

фиксированной плоскости

(определяе-

мой

начальными

условиями).

1 ОБЩИЕ СВЕДЕНИЯ

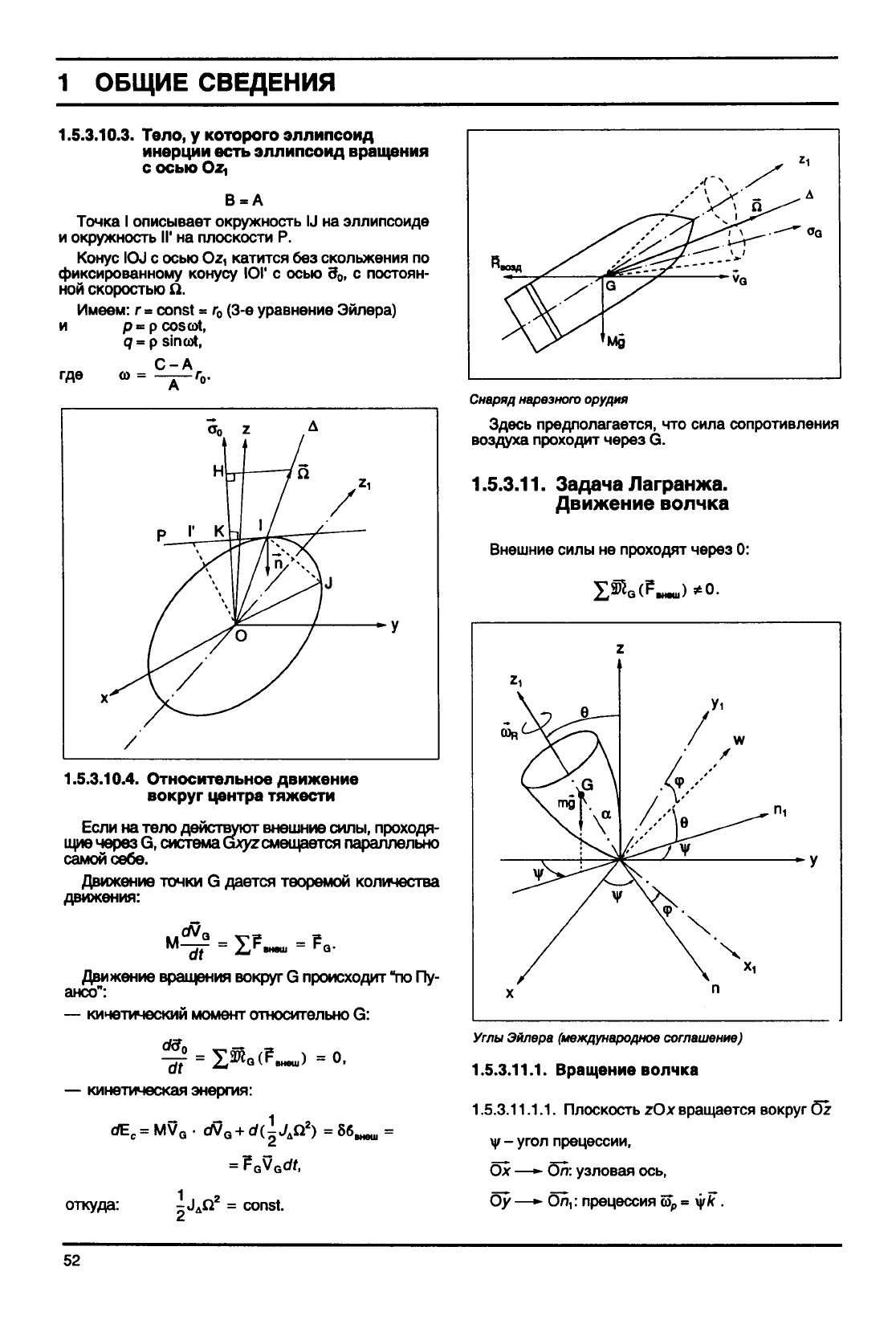
1.5.3.10.3.

Тело, у которого эллипсоид

инерции есть эллипсоид вращения

осью

Oz,

В = А

Точка

I описывает окружность IJ на эллипсоиде

и окружность II

на плоскости Р.

Конус IOJ с осью Oz, катится без скольжения по

фиксированному конусу ЮГ с осью 3

. с постоян-

ной скоростью Q.

Имеем:

г = const = г

(3-е уравнение Эйлера)

и р = р cos

cot,

qr = р sincot,

С-А

где <о = —j— г

1.5.3.10.4.

Относительное движение

вокруг центра тяжести

Если

на

тело

действуют внешние силы, проходя-

щие через G, система

Gxyz

смещается

параллельно

самой себе.

Движение точки Q дается теоремой количества

движения:

М-

Движение вращения вокруг G происходит "по Пу-

ансо":

— кинетический момент относительно G:

— кинетическая энергия:

Снаряд

нарезною

орудия

Здесь предполагается, что сила сопротивления

воздуха проходит через G.

1.5.3.11.

Задача

Лагранжа.

Движение

волчка

Внешние силы не проходят через 0:

откуда: ^tM = const.

Углы

Эйлера

(международное

соглашение)

1.5.3.11.1.

Вращение волчка

1.5.3.11.1.1.

Плоскость zOx вращается вокруг 6z

V - угол прецессии,

Ох —*~ On: узловая ось,

Оу —•- бл,: прецессия ш

= \j/F.

1 ОБЩИЕ СВЕДЕНИЯ

1.5.3.11.1.2. Плоскость zOn вращается вокруг бл,

узловой оси

67?! —

9-угол нутации,

нутация - c5

= ёл

1.5.3.11.2.

Плоскость иОл вращается вокруг

5z,

ф-угол

бл—

Gw —

зраще

Собственное вращение: З

= ф^ .

1.5.3.11.3. Движение волчка

п =

уАГ+влЧф£,

- мгновенное вращение.

Волчок неподвижен в системе

Охфг\

и:

(

£= sin в (sin ф

•

Г, + cos ф

•

/,) + cos 9- ^

/Т = cos ф • Г, - sin ф

•

Составляющие б в системе

Ox^z^R,)

таковы:

\j/

Sin 6 Sin ф + 8

СО8ф

= ijf sin 6 cos ф - в в1пф

у cosO + ф

Напомним уравнения Эйлера:

Cr+(B-A)p<7 = 3R

- /Fi = N

Поскольку на волчок действует вес

mQ,

имеем:

JfJo

- тда sin 6 (cos ф

•

- sin ф

•

yj).

В силу его вращательной симметрии А - В, от-

куда:

ГАр+

(C-A)gr= mga sin в cos ф

•jAq+

(A-C)rp = -mga sin в cos ф

LCr=O

Эта система допускает три следующих первых

интеграла:

+ V cos в = г

= const;

(1)

сохранение кинетического момента относитель-

но 55: a

= 6

- Л дает:

= Ay sin

9 + Cr

cos в = Cr

K (2)

постоянно, поскольку (55 л

trig)

•

И- 0;

сохранение механической

энергии:

Е = Е„+ Е

= ^ (Ар

+ Aq? + С/

) + /ngz = const,

откуда:

sin

8 + 6 ) +-C% + mga cos в = const.

= =

(3)

Движение волчка зависит от

начальных

условий.

Исследование показывает, что угол нутации за-

ключен между двумя значениями в, и 8

. Произ-

вольная

точка оси волчка описывает на сфере с

центром 0 кривую, которая может иметь различ-

ные формы.

Траектория

подвижною конца волчка

1.5.3.11.4.

Гироскоп

Чем больше

начальное

вращение ф

, тем ближе

друг к другу в, и в*

Впрочем,

в этом

случае

6 - const.

Нутационное движение пренебрежимо, и:

у - —=- = const - гироскопическое приближение.

Сф

Пример

гироскопа.

Гироскопический

волчок