Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.

81
Рассмотренные функции П, U, I называют потенциалами, так как их разность равна
тому или иному виду работы.
Кроме адиабатической системы существуют, как говорят, “сопряженные” с окружающей
средой термодинамические системы, которые могут обмениваться с окружающей средой теп-
лотой и работой. В этих системах вводятся в рассмотрение такие термодинамические функ-
ции как свободная энергия или изохорно-изотермический потенциал (потенциал Гельмголь-
ца)
TSUF
−
=
, (7.1)
где TS- так называемая связанная энергия, свободная энтальпия или изобарно-
изотермический потенциал (потенциал Гиббса)
TSI
−
=
Φ
. (7.2)
Получим выражения для дифференциалов этих функций.
Вычитая d(TS) из левой и правой частей уравнения pdVTdSdU
−
=
, получим
pdVSdTTSUd
−
−
=
−
)( , или
pdVSdTdF
−
−
=
. (7.3)
Выполнив аналогичные выкладки с уравнением VdpTdSdI
+
=
, найдем дифференциал сво-
бодной энтальпии
VdpTSdTdSTSId
+
−
=
−
)()( ,
VdpSdTd
+
−
=
Φ
. (7.4)
Из (7.3) легко видеть, что элементарная работа изменения объема при dT=0 равна убыли сво-
бодной энергии
dFdL
−
=
. (7.5)
Интегрируя (7.4) при dT=0 с учетом уравнения состояния идеального газа получим
)ln(
1
2
21
p
p
GRT
Ф
=∆
−
. Однако для реальных газов изменение потенциала Гиббса записы-
вают через летучесть f
)ln(
1
2
21
f
f
GRT
Ф
=∆
−
(это понятие было введено в термодинамику
Льюисом в 1901 г.). Связь между p и f найдем из выражения
RT
l
p
f
∆
−=
ln , где
−
∆
l разность между удельными работами совершаемыми идеальным и реальным газами
в изотермическом процессе. При p
→
0 )1)/(lim
0
=
→
pf
p
.
Если ТС при dT=0 кроме работы изменения объема совершает другие виды работ (в
магнитных, электрических, гравитационных полях, против сил поверхностного натяжения и
т.д.), то их сумма равна убыли свободной энергии
dFdLdL
n
i
Vi
−=+
∑
=1
, (7.5а)
где
∑
=
n
i
Vi
dL
1
- сумма элементарных работ, не связанных с изменением объема.
Термодинамические потенциалы U, I, F и
Φ
широко используются при рассмотрении фа-
зовых переходов, вопросов устойчивости ТС, процессов, сопровождающихся химическими
реакциями, процессов в гальванических и топливных элементах ( в топливном элементе хи-
мическая энергия топлива с помощью окислителя превращается в электрическую энергию).
82
При изучении таких систем применяются уравнения Гиббса-Гельмгольца
p
T
TTSI
∂
Φ∂
−Φ=+Φ=
, (7.6)
V
T
F
TFTSFU
∂
∂
−=+=
. (7.7)
Используя эти уравнения для двух любых точек процесса, можно написать
p
T
TI
∂
∆Φ∂
−∆Φ=∆
, (7.8)
V
T
F
TFU
∂
∆∂
−∆=∆
. (7.9)
Так как максимальная работа химической реакции при p=const и
Т
=const
∆Φ−=
р
max
L , а VpUIQ
p
∆+∆=∆=
, то (7.8) перепишем в виде
p
p
T
L
TLQ
∂
∂
+−=
р
max
р
max
. (7.10)
Для изохорно-изотермической системы будем иметь
FL
∆
−
=
max v
, UQ
V
∆=
,
V
V
T
L
TLQ
∂
∂
+−=
vmax
vmax
. (7.11)
В общем виде уравнение Гиббса-Гельмгольца имеет вид
x
x
x
T
L
TLQ
∂
∂
+−=
max
xmax
. (7.12)
При анализе, например, гальванического элемента (при обратимом протекании про-
цессов), используя уравнение Гиббса-Гельмгольца, можно определить электродвижущую си-
лу
Е
элемента. Так как работа по переносу электрического заряда
EnL
*
р
max
Φ=
, где Ф
*
- по-
стоянная Фарадея;
п
- валентность, а
∆Φ−=
р
max
L , то можно написать
EnL
*
р
max
Φ−=−=∆Φ
. (7.13)
Подставляя (7.13) в (7.8), получим
*
Φ
∆
−
∂
∂
=
n
I
T
E
TE
p
. (7.14)
Рассмотренные функции U, I, F,
Φ
называются также характеристическими функция-
ми, так как их частные производные определяют термодинамические параметры системы.
Так, из
pdV
TdS
dU
−
=
соответственно получим
T
S
U
V
=
∂
∂
, (7.15)
p
V
U
S
−=
∂
∂
. (7.16)
Взяв частные производные от
VdpTdSdI
+
=
при S=const или p=const
найдем

83
V
p
I
S
=
∂
∂
, (7.17)
T
S
I
p
=
∂
∂
. (7.18)
Из (7.3) и (7.4) получим
S
T
F
V
−=
∂
∂
, (7.19)
p
V
F
T
−=
∂
∂
, (7.20)
S
T
p
−=
∂
Φ∂
, (7.21)
V
p
T
=
∂
Φ∂
. (7.22)
Дифференциальные уравнения термодинамики
При анализе термодинамических систем или решении задач часто необходимо одни ча-
стные производные выразить через другие, значения которых могут быть получены из опыта,
например,
p
p
v
v
T
i
с
T
u
с
∂
∂
=
∂
∂
=
,
. Замена одних частных производных через другие в диф-
ференциальных уравнениях может упростить уравнения, облегчить их решение, или привести
к виду, более удобному для термодинамического анализа (см. тему “дросселирование газов и
паров”). Под дифференциальными уравнениями будем понимать не только уравнения, со-
держащие частные производные, но и выражения, устанавливающие связь между ними. К по-
следним относятся уравнения Максвелла. Получим их.
Приравняем уравнения (7.15)-(7.22), содержащие одинаковые правые части, например,
(7.15) и (7.18), (7.17) и (7.22) и т.д.:
T
S
I
S
U
pV
=
∂
∂
=
∂
∂
, (7.23)
p
V
F
V
U
TS
−=
∂
∂
=
∂
∂
, (7.24)
V
pp
I
TS
=
∂
Φ∂
=
∂
∂
, (7.25)
S
TT
F
pV
−=
∂
Φ∂
=
∂
∂
. (7.26)
Возьмем смешанные производные от (7.23)-(7.26)
S
V
T
SV
U
∂
∂
=
∂∂
∂
2
, (7.27)
V
S
p
VS
U
∂
∂
−=
∂∂
∂
2
, (7.28)

84
S
p
T
Sp
I
∂
∂
=
∂∂
∂
2
, (7.29)
p
S
V
pS
I
∂
∂
=
∂∂
∂
2
, (7.30)
V
T
p
VT
F
∂
∂
−=
∂∂
∂
2
, (7.31)
T
V
S
TV
F
∂
∂
−=
∂∂
∂
2
, (7.32)
p
T
V
pT
∂
∂
=
∂∂
Φ∂
2
, (7.33)
T
p
S
Tp
∂
∂
−=
∂∂
Φ∂
2
, (7.34)
Из курса высшей математики известно, что значения смешанных производных не за-
висят от порядка дифференцирования, поэтому, приравнивая (7.27) и (7.28), получим одно из
дифференциальных уравнений Максвелла
VS
S
p
V
T
∂
∂
−=
∂
∂
. (7.35)
Приравнивая (7.29) и (7.30), (7.31) и (7.32), (7.33) и (7.34) запишем остальные уравнения Мак-
свелла:
p
S
S
V
p
T
∂
∂
=
∂
∂
, (7.36)
TV
V
S
T
p
∂
∂
=
∂
∂
, (7.37)
T
p
p
S
T
V
∂
∂
−=
∂
∂
. (7.38)
Получим дифференциальное уравнение, связывающее частные производные от терми-
ческих параметров. Так как
(
)
vpfT
,
=
, то после дифференцирования будем иметь
dv
v
T
dp
p
T
dT
p
v
∂
∂
+
∂
∂
= . (а)
Полагая T=const, найдем, что
pT
v
v
T
v
p
p
T
∂
∂
−=
∂
∂
∂
∂
, (b)
или
1
−=
∂
∂
∂
∂
∂
∂
pT
v
T
v
v
p
p
T
. (7.39)
Найдем частные производные внутренней энергии и энтальпии. Из объединенного за-
кона термодинамики для обратимых процессов
pdVTdSdU
−
=
получим зависимость U от
V при T=const
85
p
V
S
T
V
U
TT
−
∂
∂
=
∂
∂
. (7.40)
Используя уравнение Максвелла
VT
T
p
V
S
∂
∂
=
∂
∂
, перепишем (7.40) в виде
p
T
p
T
V
U
VT
−
∂
∂
=
∂
∂
. (7.41)
Полученное уравнение часто называют уравнением состояния реального газа в диффе-
ренциальной форме. Оно связывает между собой калорические и термические параметры.
Для идеального газа 0=
∂
∂
T
V
U
, а
v
R
T
p
v
=
∂
∂
, тогда 0=− p
v
R
T или RTpv
=
.
Зависимость внутренней энергии от давления при T=const найдем из уравнений
TTT
p
V
p
p
S
T
p
U
∂
∂
−
∂
∂
=
∂
∂
. (7.42)
С учетом того, что
p
T
T
V
p
S
∂
∂
−=
∂
∂
, будем иметь
T
p
T
p
V
p
T
V
T
p
U
∂
∂
−
∂
∂
−=
∂
∂
. (7.43)
Частные производные для энтальпии найдем из уравнения
VdpTdSdI
+
=
:
TVTTT
V
p
V
T
p
T
V
p
V
V
S
T
V
I
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
=
∂
∂
, (7.44)
V
T
V
T
p
p
V
p
S
T
p
I
p
TTT
+
∂
∂
−=
∂
∂
+
∂
∂
=
∂
∂
. (7.45)
Выведем некоторые дифференциальные уравнения для теплоемкостей.
dvp
v
u
dTcTds
T
v
+
∂
∂
+= , (7.46)
откуда при dv=0
v
v
T
s
Tc
∂
∂
= . (7.47)
Так как
(
)
vTfs ,= , то при s=const
svsTv
T
v
T
p
T
v
v
s
T
s
∂
∂
∂
∂
−=
∂
∂
∂
∂
−=
∂
∂
. (7.48)
Таким образом,
sv
v
T
v
T
p
Tc
∂
∂
∂
∂
−= . (а)
Из dpv
p
i
dTcTds
T
p
−
∂
∂
+= при p=const следует
p
p
T
s
Tc
∂
∂
=
, (7.49)

86
но
(
)
Tpfs ,=
, следовательно, при ds=0 будем иметь
sps
T
p
T
p
T
v
T
p
p
s
T
s
∂
∂
∂
∂
=
∂
∂
∂
∂
−=
∂
∂
, тогда (7.49) перепишем в виде
sp
p
T
p
T
v
Tc
∂
∂
∂
∂
= . (b)
Вычитая (а) из (b), найдем связь между с
р
и с
v
:
∂
∂
∂
∂
+
∂
∂
∂
∂
=−
svsp
vp
T
v
T
p
T
p
T
v
Tcc
.
(с)
Приравнивая уравнения
dvp
v
u
dTcdq
T
v
+
∂
∂
+=
и
dpv
p
i
dTcdq
T
p
−
∂
∂
+=
при
dp=
0,
найдем что
pT
vp
T
v
p
v
u
cc
∂
∂
+
∂
∂
=−
. (7.50)
Для идеального газа
0=
∂
∂
T
v
u
,
p
R
T
v
p
=
∂
∂
, тогда Rcc
vp
=− .
8. Равновесие термодинамических систем
и фазовые переходы
Термодинамическое равновесие, четыре случая сопряжения
термодинамической системы с окружающей средой
Термодинамические системы можно разделить на системы, не обменивающиеся теп-
лотой с окружающей средой (адиабатические системы) и системы, которые могут обмени-
ваться с окружающей средой теплотой и работой. Установим признаки перехода ТС в
равновесное состояние и определим, какими свойствами характеризуется система в со-
стоянии равновесия.
1.
Для изолированной ТС из объединенного закона термодинамики
pdVdUTdS
+
≥
при dU=0 и dV=0 получим dS>0, т.е. увеличение энтропии в адиабати-
ческой ТС служит признаком перехода ее в равновесное состояние. В равновесном со-
стоянии dS=0, d
2
S<0, т.е. S=S
max
. Таким образом, когда адиабатическая система приходит
в равновесное состояние, энтропия системы достигает максимального значения.
2.
ТС обменивается с окружающей средой теплотой, но так, что S=const и V=const. Для
такой ТС можно написать pdVTdSdU
−
≤
, откуда при dS=0 и dV=0 получаем dU<0, т.е
уменьшение внутренней энергии ТС служит признаком стремления ее к равновесному со-
стоянию. В состоянии равновесия
dU=0, d
2
U>0, т.е. U=U
min
.
3. ТС обменивается с окружающей средой теплотой и работой, но так, что p=const и
S=const. Из VdpTdSdI
−
≤
при dp=0 и dS=0 получим dI<0 - признак перехода системы в
равновесное состояние. В состоянии равновесия dI=0, d
2
I>0, т.е. I=I
min
.
4. ТС обменивается с окружающей средой теплотой, но при этом T=const и V=const. Из
полного дифференциала свободной энергии (см. раздел “термодинамические потенциа-
лы”) pdVSdTdF
−
−
≤
при dT=0 и dV=0 будем иметь dF<0. В состоянии равновесия
dF=0, d
2
F>0, F=F
min
.
5.
ТС обменивается с окружающей средой теплотой и работой, но так, что T=const и
p=const. Тогда из VdpSdTd
+
−
≤
Φ
при dT=0 и dр=0 при переходе системы в равновесное
состояние получим dФ<0. В состоянии равновесия dФ=0, d
2
Ф>0, Ф=Ф
min
.
87
Химический потенциал
При рассмотрении фазовых переходов, когда имеют место испарение и конденсация
веществ, особое место занимает удельный изобарно-изотермический потенциал (удельный
потенциал Гиббса) Tsi
−
=
ϕ
, получивший название химического потенциала.
Выразим потенциал Гиббса через химический потенциал и массу вещества G:
ϕ
G
=
Φ
. После дифференцирования будем иметь
(
)
dGvdpsdTGdGGdd
ϕϕϕ
++−=+=Φ
.
При dT=0 и dр=0
ϕ
=
∂
Φ∂
pT
G
,
, (8.1)
т.е. химический потенциал связан с изменением массы в ТС.
Рассмотрим свободную энергию и определим
TV
G
F
,
∂
∂
.
(
)
., fdGGpdvGsdTfdGpdvsdTGfdGGdfdFGfF +−−=+−−=+==
(а)
Выразим Gdv как функцию V и G.
vdGdVGdvvdGGdvdVGvV
−
=
⇒
+
=
=
,, . (b)
Подставим (b) в (а)
(
)
dGpvfpdVSdTdF ++−−=
. (8.2)
При dT=0 и dV=0 получим
pvf
G
F
TV
+=
∂
∂
,
. (8.3)
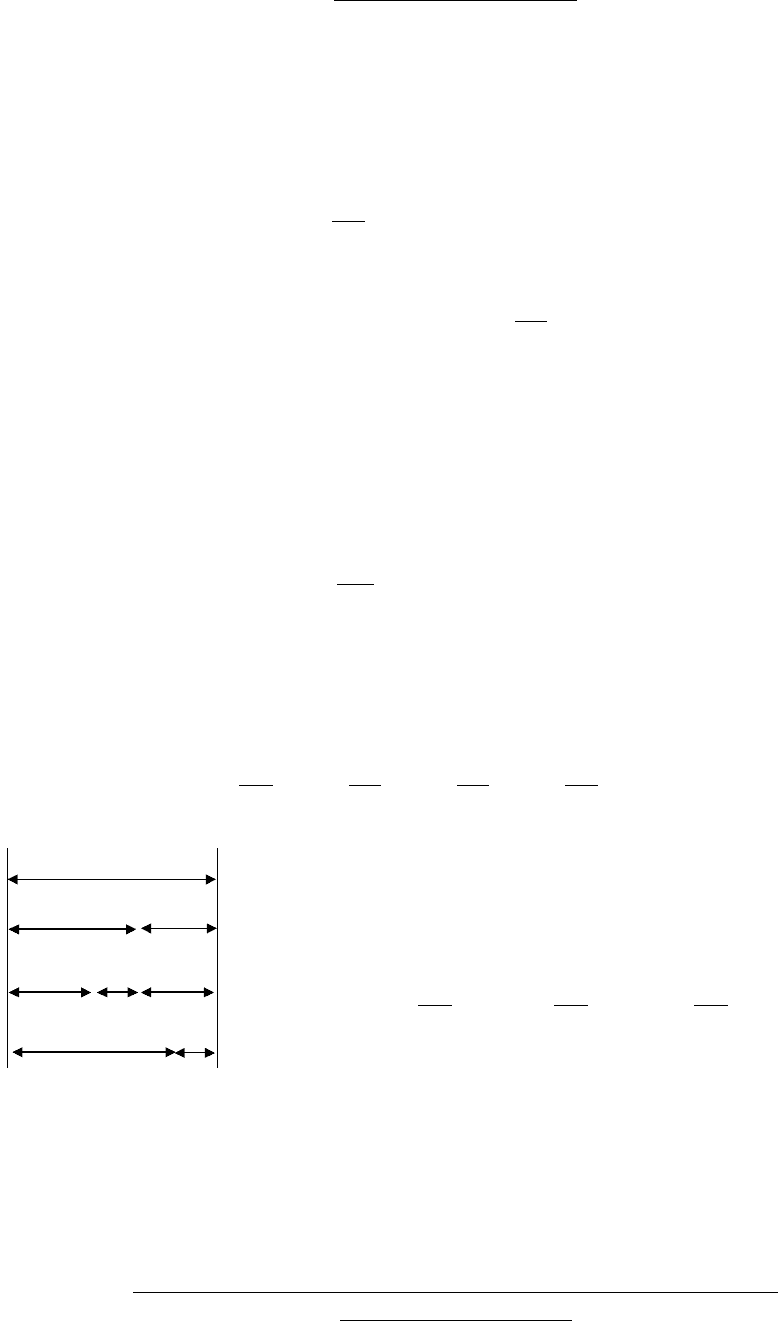
Покажем, что
ϕ
=
+
pvf . Для этого рассмотрим диаграмму потенциалов, из которой
видно, что
Φ
=
+
+
Φ
=
+
+
pVFTSpVTSF , . Разделив на массу, получим
ϕ
=
+
pvf .
Произведя подобные выкладки для U и I, будем иметь
ϕ
=
∂
Φ∂
=
∂
∂
=
∂
∂
=
∂
∂
TpTVSpSV
GG
F
G
I
G
U
,,,,
.
Таким образом, химический потенциал позволяет определить из-
менение любой характеристической функции при изменении ко-
личества вещества в фазовых превращениях. Внутренняя энергия
фазы в такой системе - функция трех переменных
(
)
GVSfU ,,=
,
тогда
,
,,,
dGpdVTdS
dG
G
U
dV
V
U
dS
S
U
dU
SVGSGV
ϕ
+−=
=
∂
∂
+
∂
∂
+
∂
∂
=
откуда
dGpdVdUTdS
ϕ
−
+
=
. (8.4)
Объединенный закон термодинамики для системы с фазовыми переходами и с уче-
том работ L
Vi
, не связанных с изменением объема, имеет вид (m – число фаз):
∑∑
==
+−+≥
n
i
Vi
m
j
jj
dLdGpdVdUTdS
11
ϕ
. (8.5)
Условия устойчивости и равновесия в изолированной системе.
Условия устойчивости
Термодинамический анализ показывает, что ТС будет механичски
I
U
F
Ф
TS
TS
pV
pV
Рис. 8.1

88
устойчивой, если
0<
∂
∂
T
v
p
. Тепловая устойчивость системы выражается неравен-
ством с
v
>0. Действительно, если
0>
∂
∂
T
v
p
, то увеличение объема приведет к росту дав-
ления в системе и дальнейшему ее расширению, т.е. ТС все дальше и дальше будет ухо-
дить от равновесного состояния. При с
v
<0 подвод теплоты приводит к уменьшению
температуры системы, т.е. к росту температурного напора между ТС и окружающей сре-
дой и увеличению теплоподвода к ТС - процесс также становится лавинообразным.
Условия равновесия в однородной изолированной системе
Было показано, что для изолированной системы, когда dU=0 и dV=0, в состоянии рав-
новесия dS
c
=0. Будем считать, что ТС состоит из двух подсистем
1 и 2, тогда
0
21
=+= dSdSdS
c
,
(а)
но
1
1
1
1
1
1
dV
T
p
T
dU
dS +=
, (b)
2
2
2
2
2
2
dV
T
p
T
dU
dS +=
. (с)
Так как
U
c
=U
1
+
U
2
=const, то
dU
2
=-
dU
1
. (d)
Аналогично, из
V
c
=V
1
+
V
2
=const следует
dV
1
= -
dV
2
. (e)
Подставив (b) и (с) в (а) с учетом (d) и (е), получим
0
11
1
2
2
1
1
1
21
=
−+
−= dV
T
p
T
p
dU
TT
dS
c
, (8.6)
но
dU
1
и
dV
1
не равны нулю, следовательно,
=
=
.
21
21
pp
TT
(8.7)
Таким образом, изолированная однородная ТС будет находиться в равновесии в
том случае, если во всех точках ТС одинаковые давление и температура.
Условия фазового равновесия
Рассмотрим систему, состоящую из двух фаз. Как и в предыдущем случае, в состоянии
равновесия системы
0
21
=+= dSdSdS
c
, (а)
1
1
1
1
1
1
1
1
1
dG
T
dV
T
p
T
dU
dS
ϕ
−+=
, (b
)
2
2
2
2
2
2
2
2
2
dG
T
dV
T
p
T
dU
dS
ϕ
−+=
. (с)
Так как
U
c
=U
1
+
U
2
,
V
c
=V
1
+
V
2
и
G
c
=G
1
+
G
2
, то
dU
2
=-
dU
1
, (d)
dV
1
= -
dV
2
,
dG
1
=-
dG
2
. Подставляя (b) и (с) в (а) с учетом последних равенств, получим
0
11
1
2
2
1
1
1
2
2
1
1
1
21
=
−−
−+
−= dG
TT
dV
T
p
T
p
dU
TT
dS
c
ϕϕ
, (8.8)
так как
dU
1
,
dV
1
и
dG
1
не равны нулю, следовательно,
1
2
Рис. 8.2
1- жидкость
2- пар
Рис. 8.3
89
=
=
=
,
21
21
21
ϕϕ
pp
TT
(8.9)
т.е. чтобы в изолированной ТС не происходили фазовые переходы, необходимо равенство
температур, давлений и химических потенциалов фаз. В действительности равновесие яв-
ляется динамическим: фазовый переход имеет место, но число молекул, покинувших по-
верхность жидкости, равно числу молекул, возвратившихся из пара в жидкость.
Фазовые переходы. Правило фаз Гиббса
Рассмотрим фазовые переходы в р
-
Т
диаграмме вещества. Любое
вещество может находиться в трех агрегатных состояниях: жидком, газообразном и в виде
твердого вещества, в котором при определенных физических условиях может быть не-
сколько фаз (например, железо может состоять из
α
-железа и
β
-железа).
На р
-
Т
диаграмме агрегатные состояния раз-
делены линиями фазовых переходов. АО-
линия сублимации, ОВ- линия плавления,
ОК- линия испарения. В точке О, которая
называется главной тройной точкой (для во-
ды р
тт
=610,8 Па,
t
тт
=0,01 С), вещество нахо-
дится одновременно в трех агрегатных со-
стояниях. В дальнейшем, если не будет
особо оговорено, под фазами будем пони-
мать агрегатные состояния вещества. В точ-
ке К вещество находится в критическом со-
стоянии, здесь теряется понятие жидкости и
пара (газа), так как
v
ж
=
v
п
=
v
, теплота парооб-
разования и коэффициент поверхностного
натяжения равны нулю. Если подвод теплоты при постоянном давлении осуществляется
при р
1
>р
тт
(см. рис.8.4), то вещество из твердого состояния переходит в жидкое, а затем в
газообразное, однако если р
2
<р
тт
, то при нагреве сразу происходит переход из твердого в
газообразное состояние.
Правило фаз Гиббса устанавливает зависимость степени свободы ТС (т.е. числа неза-
висимых переменных) от числа компонентов и фаз в системе:
2
+
−
=
rn
ψ
, (8.10)
где п- число компонентов системы,
r-
число фаз в системе.
Для чистого вещества, например, кислорода О
2
, п
=
1,
r=
1,
ψ
=2. В такой системе
можно произвольно изменять два параметра, третий же является зависимым, определяе-
мым уравнением состояния (например,
(
)
vTfp ,=
).
Для однокомпонентной системы, состоящей из двух фаз, например, воды и водяного
пара п
=
1,
r=
2,
ψ
=1. В этом случае лишь один параметр можно выбирать произвольно.
Так, энтропия и энтальпия сухого насыщенного пара, энтропия и энтальпия насыщенной
жидкости однозначно определяются только температурой (или только давлением, так как
в двухфазной области
(
)
Tfp =
).
В главной тройной точке п
=
1,
r=
3,
ψ
=0, т.е. существование вещества в таком состоя-
нии возможно только при единственном для каждого вещества сочетании температуры и
давления.
p
T
dp
dT
p
1
p
2
1
2
газ
жидкость
тв. тело
О
А
В
К
Рис. 8.4

90
Уравнение Клапейрона-Клаузиуса
Было показано, что условиями термодинамического равновесия являются равенства
Т
ж
=
Т
п
, р
ж
=
р
п
, и
ϕ
ж
=
ϕ
п
. Рассмотрим процесс вдоль кривой ОК (рис.8.4). В точке 1 имеет
место равенство
(
)
(
)
pTpT ,,
п1ж1
ϕϕ
=
.
Изменим температуру и давление на
dT
и
dp
так, чтобы точка 2 осталась на кривой ОК. В
новой точке снова получим
(
)
(
)
dppdTTdppdTT ++=++ ,,
п1ж2
ϕϕ
,
или
пп1жж1
ϕϕϕϕ
dd +=+
, но
п1ж1
ϕϕ
=
, тогда
пж
ϕϕ
dd =
. Раскрывая полные дифференциа-
лы
пж
и
ϕϕ
dd
, получим
dpvdTsdpvdTs
ппжж
+−=+−
, откуда
жп
жп
vv
ss
dT
dp
−
−
=
. (8.11)
Уравнение (8.11) называется уравнением Клапейрона-Клаузиуса и может быть применено
ко всем фазовым превращениям чистых веществ.
В термодинамике принято жидкую и газообразную фазы, находящиеся в равновесии
(когда состояние вещества изображается точкой на кривой ОК) обозначать надстрочными
индексами
′
для жидкости и
″
для пара, и называть их соответственно насыщенной жид-
костью и сухим насыщенным паром. Так как
T
r
ss =
′
−
′′
, где
r
- удельная теплота парооб-
разования, Т
-
температура насыщения, то уравнение (8.11) можно переписать в виде
( )
vvT
r
dT
dp
′
−
′′
=
. (8.12)
Проинтегрировав уравнение Клапейрона-Клаузиуса, найдем связь между давлением и
температурой насыщения
( )
∫
+
′
−
′′
= constdT
vvT
r
p
s
. (8.13)
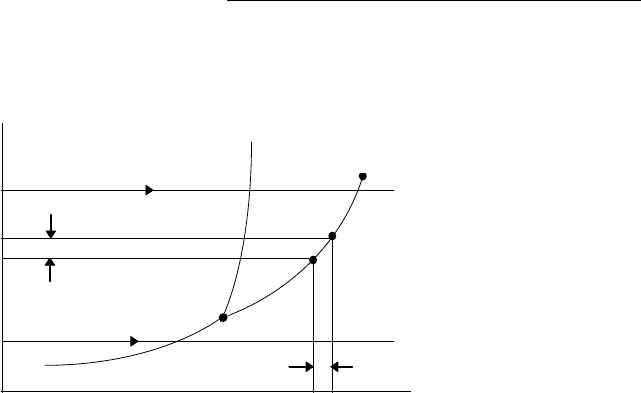
Устойчивость фаз
При рассмотрении процессов с фазовыми переходами возникает вопрос, при каких
условиях масса одной из фаз будет увеличиваться за счет другой (фаза, у которой
dG>
0
называется устойчивой).
Рассмотрим ход кривых )(
pf
=
ϕ
при
T=
const в
ϕ
-
р
диаграмме. Из полного диффе-
ренциала
ϕ
:
vdpsdTd
+
−
=
ϕ
при
T=
const получим
v
p
T
=
∂
∂
ϕ
. Так как
v
″
>v
′
, то
TT
pp
∂
∂
>
∂
∂
жп
ϕϕ
, т.е. в
ϕ
-
р диаграмме
