Барилович В.А. Основы термогазодинамики двухфазных потоков и их численное решение

20

()

1

2

4

2

−

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

++

=

M

w

Tcva

dx

dF

F

Tca

w

D

c

Tca

wD

vq

dx

dp

VS

f

VS

w

. (2.30)

Для адиабатического канала (

q

w

=0) получим

()

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

+

−

=

dx

dF

F

Tca

w

D

c

Mv

w

dx

dp

VS

f

1

2

1

2

. (2.31)

При изоэнтропийном течении (

с

f

=0) гомогенного потока в канале будем

иметь

(

)

dx

dF

FMv

w

dx

dp

1

2

−

−=

, но

kpva

S

=

2

, откуда

kp

a

v

S

2

= , тогда

(

)

dx

dF

FM

kpM

dx

dp

1

2

−

=

,

где

k определяется по формуле (2.18).

На основании системы (2.28) была составлена программа GM1QT

(приложение №2), позволяющая оценить роль различных воздействий на

гомогенный пароводяной поток.

Для адиабатического цилиндрического канала

0=

dx

dF

и формула (2.31)

принимает вид

()

⎟

⎠

⎞

⎜

⎝

⎛

+

−

=

Tca

w

D

c

Mv

w

dx

dp

VS

f

2

1

2

1

. (2.32)

Используя уравнение (2.32) совместно с уравнениями

()

dx

dp

r

T

vv

dx

dT

dx

dw

w

v

dx

dv

D

w

f

c

dx

dp

w

v

dx

dw

′

−

′′

==−−= ,,

2

,

можно определить при заданных диаметре канала и расходе длину

цилиндрической трубы, которая пропустит заданный критический

(максимальный) расход и величину критического давления на выходном срезе

трубы (см. рис.2.1и программу GM1_CILS в приложении №2). Решение данной

задачи позволяет дать ответ и на один из важнейших вопросов – каким будет

критический расход при заданных

начальных параметрах и относительной

длине трубы

DLL = . Знание характеристик потока на срезе разорвавшейся

трубы позволяет создавать рациональные аварийные системы в тепловой и

атомной энергетике.

21

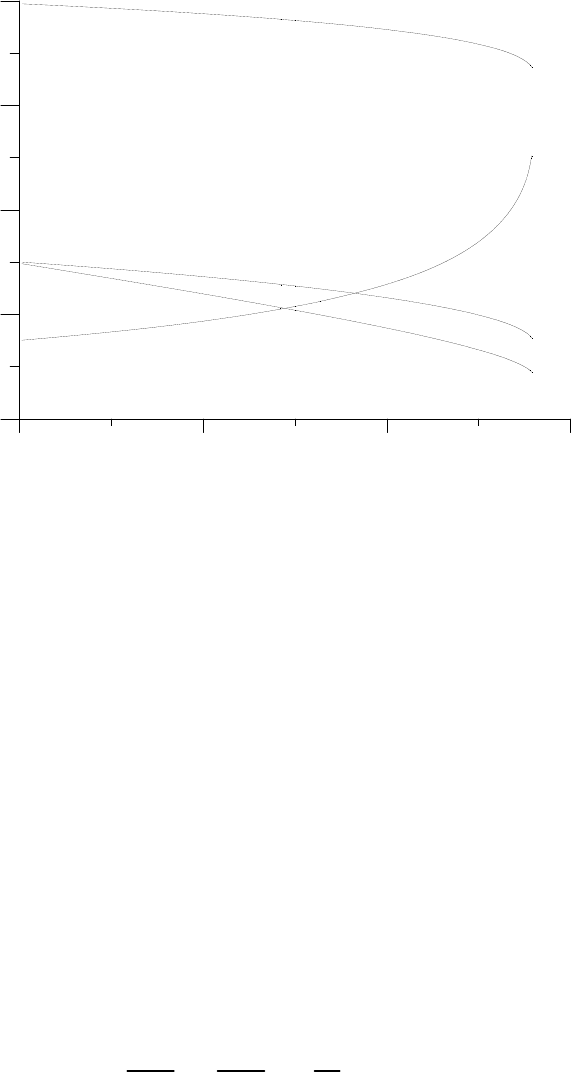
0.00 0.20 0.40 0.60

0.00

40.00

80.00

120.00

160.00

Т, К

Рис. 2.1

3. Дисперсно-кольцевое течение

3.1. Уравнения сохранения потока массы

Рассмотрим движение двухфазного одномерного однокомпонентного

потока в адиабатическом канале с непроницаемыми стенками. Выделим в

канале неподвижный элемент объемом dV=Fdx и составим уравнение баланса

элементарных потоков масс (метод Эйлера) для дисперсно-кольцевого режима

течения, который при отсутствии пленки переходит в дисперсный.

Рассмотрим двухфазный

поток с испаряющимися каплями (T

к

>T

п

).

Локальное изменение массы капель в элементарном объеме в единицу времени

обусловлено изменением потока капель через его границы, уносом жидкости с

поверхности пленки (

Ун

Ed

&

), выпадением (осаждением) капель в пленку (

OC

Dd

&

)

и испарением горячих капель (

ΠΚ-

Gd

&

) , то есть

[]

dxGDE

x

dx

x

GG

OC Π−Κ

ΚΚ

−−

∂

+

∂

−=

&

&&

&

УН

∂

∂τ

∂

. (3.1)

Для стационарного потока будем иметь

Κ

Gd

&

=

Ун

Ed

&

-

OC

Dd

&

-

ΠΚ-

Gd

&

[кг/с] .

Уравнения сохранения масс парового потока и испаряющейся пленки

(

T

пл

> T

п

) будут иметь вид:

Π

Gd

&

=

ΠΚ-

Gd

&

+

ΠΛΠ−ΠΛ

dSj , (3.2)

p

⋅

10

-4

,Па

w

п

,м/c

ρ

, кг/м

3

T

п

,C

x , м

22

ΠΛ

Gd

&

=

OC

Dd

&

ΠΛΠ−ΠΛ

−− dSjEd

Ун

&

. (3.3)

где

j

ΠΛ Π−

- плотность потока массы пара, уносимого с единичной поверхности

пленки, кг/(м

2

с); dS

ΠΛ

- элементарная поверхность пленки.

Складывая (3.1),(3.2) и (3.3), получим уравнение сохранения массы для

всего потока

0=++

ΠΛΠΚ

GdGdGd

&&&

. (3.4)

Уравнение (3.4) можно записать в виде

(

)

0

=

+

ΠΛΠΛΠΛΠΠΠΚΚΚ

ρ

fwfwfwd

, (3.5)

интегрируя (3.5), получим

constfwfwfw

=

+

ΠΛΠΛΠΛΠΠΠΚΚΚ

ρ

. (3.6)

Площадь поперечного сечения канала можно представить в виде суммы

площадей, занимаемых фазами

ΠΛΠΚ

+

=

fffF . (3.7)

В маловлажных парокапельных потоках, движущихся с большой

скоростью в адиабатических каналах, в первом приближении можно считать,

что толщина пленки мала и ею можно пренебречь, то есть

f

ΠΛ

=0. Вопросы

уноса и выпадения капель в двухфазном потоке являются сложной научной

задачей, которая решена лишь частично в экспериментальном плане для

цилиндрических каналов при определенных режимных параметрах [6]. В

случае, когда

0==

Ун„м

EdDd

&&

уравнение (3.1) примет вид

Π−ΚΚ

−= GdGd

&&

.

(3.8)

Так как изменение (уменьшение) элементарного потока массы капель

dG

&

Κ

вызвано испарением капель (Т

К

>Т

П

), находящихся в объеме Fdx, то (3.8)

можно переписать так:

(

)

FdxnDjfwdGd

v

2

ΚΠ−ΚΚΚΚΚ

−==

πρ

&

, (3.9)

где

w

Κ

- скорость капельного потока, м/с;

f

Κ

- площадь поперечного сечения, занятая жидкой фазой, м

2

;

23

π

D

K

2

- поверхность капли, м

2

;

n

v -

концентрация капель (количество капель в единице объема) , 1/м

3

;

Π−Κ

j

- плотность потока испарившейся массы пара , кг/(м

2

с).

Уравнение (3.9) является дифференциальным уравнением сохранения

массы для капельного потока при дисперсном режиме течения. В ряде случаев

его более удобно записать через расход капельного потока

&

G

Κ

и диаметр

капли

D

Κ

. Для этого вначале найдем связь между концентрацией n

v

и потоком

капель

n

&

,(1/сек).

Пусть поперечное сечение канала площадью

F пронизывается потоком

капель

&

n

, тогда за время dτ в элементарном объеме Fdx окажется

&

nd

τ капель.

Так как

dτ=dx/ w

Κ

, то будем иметь

n

v

=

Fw

n

Fdxw

dxn

Fdx

dn

ΚΚ

==

&&&

τ

. (3.10)

Капельный поток массы найдем по формуле

n

D

nVG

&&

&

Κ

ΚΚΚ

==

ρ

π

ρ

6

3

. (3.11)

Умножив и разделив правую часть (3.9) на выражение 6

D

к

ρ

к

с учетом

(3.10) и (3.11) получим

()

ΚΚΚ

ΚΠ−Κ

ΚΚΚ

−=

ρ

Dw

Gj

fw

dx

d

&

6

. (3.12)

Вводя понятие интенсивности потока массы на единицу длины канала

FnDjJ

v

2

ΚΠ−ΚΠ−Κ

=

π

&

, (3.13)

перепишем формулу (3.9) в иной форме

()

Π−ΚΚΚΚ

−= Jfw

dx

d

&

ρ

. (3.14)

Уравнение сплошности для парового (несущего) потока запишется в виде

()

Π−ΚΠΠΠ

= Jfw

dx

d

&

ρ

. (3.15)

24

Складывая (3.14) и (3.15) , получим уравнение сплошности для всего

парокапельного потока, движущегося в адиабатическом канале с

непроницаемыми стенками

()

ΚΚΚ

fw

dx

d

ρ

+

()

ΠΠΠ

fw

dx

d

ρ

=0. (3.16)

Если в стационарном потоке имеет место конденсация пара на каплях и пленке

(

Т

К

< Т

П

, Т

ПЛ

< Т

П

), то уравнение сохранения элементарных потоков массы

будет иметь вид

)20.3(.

)19.3(,

)18.3(,

ОСУН

DdEdGdGd

GdGdGd

DdEdGdGd

&&

&&&

&&

+−=

−−=

−+=

ΠΛ−ΠΠΛ

ΠΛ−ΠΚ−ΠΠ

Κ−ΠΚ

Рассмотрим случай, когда парокапельный поток с испаряющимися

каплями движется в адиабатическом канале, по стенкам которого течет

холодная жидкость (

Т

ПЛ

< Т

П

). Тогда уравнения материального баланса примут

вид

Π−ΚΚ

−−= GdDdEdGd

ОСУН

&

&&

&

, (3.21)

ΠΛ−ΠΠ−ΚΠ

−= GdGdGd

&&&

, (3.22)

ΠΛ−ΠΠΛ

+−= GdEdDdGd

УНОС

&

&&

&

. (3.23)

Часто при рассмотрении задач движения двухфазного потока в каналах

необходимо выразить одни физические величины через другие с целью

приведения уравнений к более удобному для анализа или решения виду. Так,

например, выражение секундного расхода жидкой фазы для монодисперсного

потока можно представить в форме

Fw

D

nn

D

fwG

vK

K

K ΚΚ

Κ

ΚΚΚ

===

ρ

π

ρ

π

ρ

66

33

&

, (3.24)

откуда получаются следующие уравнения связи:

Fwnn

v Κ

=

&

,

Κ

=

w

nD

f

6

3

&

π

,

6

3

ΚΚ

=

D

n

F

f

v

π

.

После знакомства с записью основных уравнений сохранения потоков

массы перейдем к изучению массопереноса на границе раздела фаз.

При рассмотрении двухкомпонентных систем, когда жидкость испаряется

в несобственный пар (например, вода - воздух) локальную плотность потока

испаряющейся массы капель можно записать в виде

(

)

∞

−

=

iiwi

ccj

β

, (3.25)

где β - локальный коэффициент масcопереноса, м/с;

25

∞iiw

сс , - концентрации испаряющегося i-го вещества на поверхности

раздела жидкость-газ и на бесконечности, кг/м

3

.

Концентрация

i-го компонента в смеси может быть выражена через его

парциальное давление

смi

i

см

i

TR

p

V

G

c ==

, (3.26)

где

ii

RR

μ

0

= - газовая постоянная, Дж/(кг⋅К), R

0

=8314 Дж/(кмоль⋅К)-

универсальная газовая постоянная;

μ

i

– молекулярная масса, которая для паров воды равна 18 кг/кмоль.

Коэффициент массопереноса определяют из критериальных уравнений.

Так, например, при обтекании газом плоской поверхности испаряющегося

вещества при ламинарном течении газа (

г

Re

ν

lw

=<10

5

) можно написать

33,00,5

г

Re646,0 Sc

D

l

Sh ==

β

, (3.27)

где

Sh – критерий Шервуда;

D

Sc

г

ν

= - критерий Шмидта;

()

∫

=

l

dxx

l

0

1

ββ

- средний коэффициент массопереноса; l – длина пластины;

p

T

DD

n

0

⎟

⎠

⎞

⎜

⎝

⎛

=

- коэффициент диффузии, м

2

/с; D

0

=22⋅10

-6

м

2

/с –

коэффициент диффузии для системы вода-воздух при нормальных условиях

(

р

0

=760 мм рт. ст.=760/750 ⋅ 10

5

Па, Т

0

=273 К); n=1,5…2,5.

При обтекании газовым потоком капли

β

находят из критериального

уравнения

33,05,0

Re6,02 ScSh += , (3.28)

где

г

кгк

Re

ν

wwD −

=

;

D

Sh

к

β

= ; D

к

– диаметр капли.

В формуле (3.28) первое слагаемое в правой части определяет

массоперенос на молекулярном уровне, второе – на молярном (за счет

конвекции), которое называется "ветровым множителем".

Вопрос массопереноса на границе жидкость - собственный пар до сих пор

остается открытым [18]. Однако в этом случае часто используют формулу

Герца-Кнудсена. Для того чтобы понять механизм

молекулярного

массопереноса рассмотрим конденсацию неподвижного чистого пара на

вертикальной стенке при

.

sw

TT <

Поток пара, конденсирующегося на

поверхности

пленки обозначим

j

п-пл

, а поток

26

пара от жидкости - j

пл-п

. Тогда результирующий поток массы пара равен

(

)

(

)

пл

пппппплплп

TT

wwjjj

s

ρ

−=−=Δ

−−

. Подставляя сюда выражение для плотности

пара из уравнения Клапейрона

пп

п

TR

p

=

ρ

и

средней скорости молекул пара, определенной

по кинетической теории

газов

получим,

2

пп

п

π

TR

w =

формулу Герца-

Кнудсена

()

⎟

⎠

⎞

⎜

⎝

⎛

−=Δ

пл

плп

п

2

1

T

Tp

T

p

R

j

s

π

. (3.28а)

Действительный результирующий поток

массы между паром и пленкой отличается от

подсчитанного по формуле (3.28а)

:

χ

jj

Δ

=

Δ

д

,

где

χ

- коэффициент конденсации,

определяемый отношением количества

захваченных пленкой молекул пара к количеству молекул, ударившихся о

поверхность пленки -

удар

захв

n

=

χ

. Более поздние исследования [23] показали,

что

()

χ

fjj Δ=Δ

д

, где

()

χ

4,01 −

=f

;

0,56

s

35

p

=

χ

.

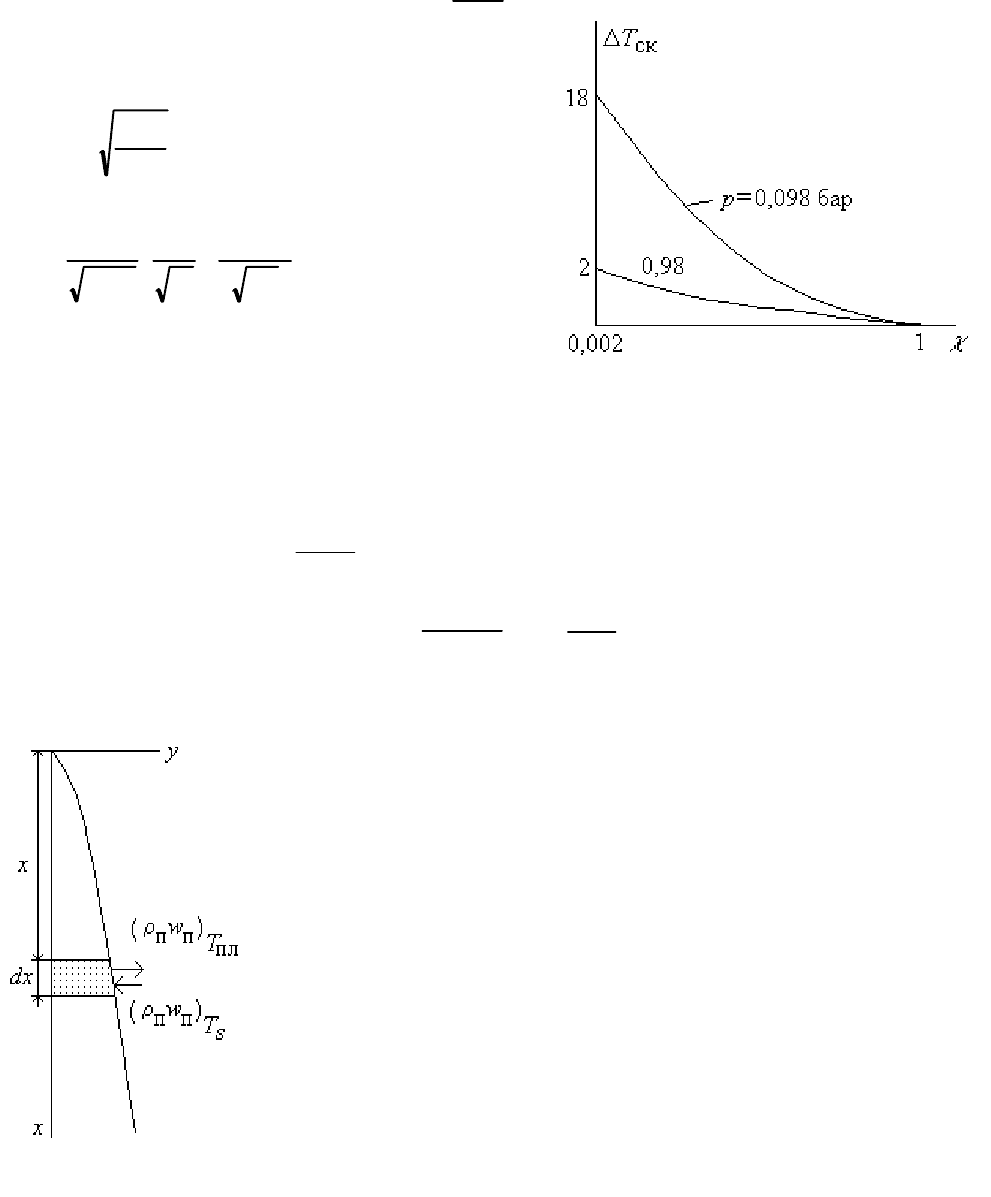
Чем больше ударившихся молекул

отражается от поверхности пленки, тем больше

скачок температур (см. рис.3.1) в кнудсеновском

слое, равном длине свободного пробега

молекулы. В этом случае термическое

сопротивление при передаче теплоты от пара к

стенке складывается из сопротивления пленки и

сопротивления на границе

раздела фаз. Зависимость

),(

ск s

рfT

χ

=Δ

характеризуется уменьшением скачка температуры

при стремлении

χ

к единице и с увеличением

давления насыщения.

При конденсации пара на холодных капля

(

Т

к

<Т

п

=Т

s

(р

п

) ) плотность потока

конденсирующегося пара может быть представлена в

виде:

Рис.3.1

Рис.3.2

27

()

(

)

пк

кп

п

конд

к-п

2

1

0,4-1

RТ

Тp

Т

p

j

π

κ

⎟

⎠

⎞

⎜

⎝

⎛

−= , (3.29)

где в качестве первого приближения коэффициент конденсации при

р

s

=700…10

5

Па можно определить по формуле [23]

56,0

конд

35

s

p

=

κ

. (3.30)

В

[]

30 , где подробно рассматриваются вопросы тепло – и массопереноса

на границе раздела фаз, приводится формула при

конд

κ

=1

п

к

кп

п

пкпк-п

2

1

)

)(

ln(515,01))((67,1

TR

T

Tp

p

pTpj

π

⎟

⎠

⎞

⎜

⎝

⎛

+−=

(3.29a)

Следует отметить, что строго говоря, формулы (3.29) и (3.29a) справедливы

лишь в случае, когда радиус капли меньше длины свободного пробега молекул

22

3

п

TR

p

l

π

μ

=

′

[5] , однако несмотря на это приведенные формулы используется

и в случае, когда

R

к

>l'. В расчетной практике также широко используется и

формула Максвелла. Так, для испаряющейся капли при

1

исп

=

κ

потность потока

пара [8]

() ()()

(

)

(

)

пп

ппкппп

ппкпп-к

2

ТR

ТpТpТR

ТТj

π

ρρ

−

=−=

. (3.31)

В дальнейшем при записи уравнений сохранения при наличии фазовых

переходов мы будем использовать символ плотности потока массы

j, не

вдаваясь в его физическую природу.

3.2. Уравнения движения

В курсе гидрогазодинамики сплошной среды [7] доказывается, что

скорость изменения количества движения некоторой материальной системы

равна главному вектору всех внешних сил, приложенных к данной системе:

R

d

Kd

r

=

τ

, (3.32)

где

∑

=

n

i

R

1

r

=R .

Рассмотрим одномерный полидисперсно-кольцевой поток, в котором

капли разбиты на группы. За время

dτ поток внесет в элементарный объем Fdx

количество движения

28

τ

dwGwGwG

n

i

ii

⎟

⎠

⎞

⎜

⎝

⎛

++

∑

=

ΠΛΠΛΚΚΠΠ

1

&&&

. (a)

За это же время из элементарного объема поток вынесет количество

движения

()

τ

dwGdwGwGdwGwGdwG

n

i

n

i

iiii

⎟

⎠

⎞

⎜

⎝

⎛

++

⎟

⎠

⎞

⎜

⎝

⎛

+++

∑∑

=

ΠΛΠΛΠΛΠΛ

=

ΚΚΚΚΠΠΠΠ

11

)(

&&&&&&

. (b)

Вычитая из (b) (a) и учитывая (3.32), получим

(

)

DdxFdpwGdwGdwGd

w

n

i

ii

πτ

−−=+

⎟

⎠

⎞

⎜

⎝

⎛

+

ΠΛΠΛ

=

ΚΚΠΠ

∑

)(

1

&&&

, (3.33)

где

τ

w

- касательное напряжение на стенке.

Здесь и в дальнейшем мы будем считать, что вязкость несущего потока

проявляет себя лишь на границах раздела капли-пар и пар-стенка.

Для монодисперсного потока будем иметь:

(

)

DdxFdpwGdwGd

w

πτ

−−=+

ΚΚΠΠ

)(

&&

. (3.34)

Если запись второго слагаемого в правой части уравнения очевидна и

представляет элементарную силу касательного напряжения на стенке, то запись

результирующей силы статического давления

Fdp нуждается в пояснении. Для

двух бесконечно близких сечений, находящихся на расстоянии

dx, имеем

площади живого сечения

F и F+dF. На площадь F действует сила статического

давления

pF , а на F+dF - сила (p+dp)(F+dF). Со стороны стенок канала поток

испытывает силу

pdF. Алгебраически складывая эти силы, получим

результирующую силу статического давления с точностью до 1-го порядка

малости

dR

x

= pF - (p+dp)(F+dF) + pdF = - Fdp .

При записи уравнения движения для составляющих потока (пара, капель,

пленки) необходимо учитывать количество движения, которое они теряют или

приобретают за счет уноса или осаждения жидкости на поверхности пленки,

испарения или конденсации массы на поверхности капель и пленки, имеющих

свои скорости. В рассматриваемом случае внутренние диссипативные силы

всего потока для составляющих

потока становятся внешними. Исходя из

сказанного, для дисперсно-кольцевого испаряющегося потока (

Т

К

> Т

П

и Т

ПЛ

>

Т

П

) можно написать:

Π−ΚΚΠΠ

= GdwwGd

&&

)( +

Π−ΠΛΠΛ

Gdw

&

- D

*

n

v

Fdx - f

n

dp-

τ

gl

ΠΛ

dS

, (3.35)

Π−ΚΚΚΚ

−= GdwwGd

&&

)( +

УН

Edw

&

ΠΛ

CO

Ddw

&

Κ

− + D

*

n

v

Fdx - f

К

dp

, (3.36)

29

Π−ΠΛΠΛΠΛΠΛ

−= GdwwGd

&&

)( -

Ун

Edw

&

ΠΛ

+

OC

Ddw

&

Κ

−

+

−fdp dS dS

gl W WΠΛ ΠΛ

τ

, (3.37)

где

()

8/

2*

ΚΠΚΠΠΚ

−−= wwwwDcD

x

ρπ

- сила сопротивления единичной

капли, которая может принимать как положительное, так и отрицательное

значение; c

x

=f(Re

K

) - коэффициент сопротивления капли;

Π

ΠΚΠΚ

Κ

−

=

μ

ρ

wwD

Re ;

μ

П

- коэффициент динамической вязкости пара;

τ

gl

- касательное напряжение,

действующее между паром и пленкой.

Отметим, что наличие примесей в потоке приводит к росту вязкости

несущей среды. Так, для потока, содержащего твердые сферические частицы,

она может быть определена по формуле Эйнштейна [22]

⎟

⎠

⎞

⎜

⎝

⎛

+=

αμ

2

5

1

*

, где

α

- объемная доля частиц.

Складывая уравнения (3.35), (3.36) и (3.37), получим (3.34). Разрешая

уравнения (3.35), (3.36) и (3.37) относительно

&

Gw

ii

с учетом (3.1), (3.2) и (3.3) ,

найдем, что

−

⎟

⎠

⎞

⎜

⎝

⎛

−−−−−=

Π−ΚΠΛ

GdwwdSFdxnDdpfdwG

КПglv

&&

τ

*

ППП

(

)

Π−ΠΛΠΛ

− Gdww

&

П

,

(3.38)

(

)

УНv

EdwwFdxnDdpfdwG

&

ΠΛΚΚΚΚ

−−+−=

*

, (3.39)

(

)

COWWgl

DdwwdSdSdpfdwG

&

ΠΛΚΠΛΠΛΠΛΠΛ

−+−+−=

ττ

, (3.40)

или разрешая относительно производных можно написать:

() ()

⎢

⎣

⎡

⎥

⎦

⎤

−−−−−−−−=

Π−ΠΛ

ΠΛ

Π−ΚΠΛ

dx

Gd

ww

dx

Gd

ww

dx

dS

FnD

dx

dp

f

G

dx

dw

glv

&&

&

пКП

*

п

τ

1

, (3.41)

()

⎥

⎦

⎤

⎢

⎣

⎡

−−+−=

ΠΛΚΚ

Κ

dx

Ed

wwFnD

dx

dp

f

G

dx

dw

v

УН

&

*

1

, (3.42)

()

⎥

⎦

⎤

⎢

⎣

⎡

−+−+−=

ΠΛΚ

ΠΛ

dx

Dd

ww

dx

dS

dx

dS

dx

dp

f

G

dx

dw

CO

W

Wgl

&

ττ

1

, (3.43)

где

FnjD

dx

Gd

vΠ−ΚΚ

Π−Κ

=

2

π

&

, кг/(с⋅м);

ΠΛΠ−ΠΛ

Π−ΠΛ

= Dj

dx

Gd

π

&

.

Для монодисперсного потока с испаряющимися каплями (Т

К

>T

П

)

уравнения (3.38) и (3.39) примут вид:

(

)

Π−ΚΚΠΠΠΠ

−−−−−= GdwwdSFdxnDdpfdwG

Wv

&&

τ

*

,

(3.44)

Барилович В.А. Основы термогазодинамики двухфазных потоков и их численное решение

Подождите немного. Документ загружается.