Барилович В.А. Основы термогазодинамики двухфазных потоков и их численное решение
Подождите немного. Документ загружается.

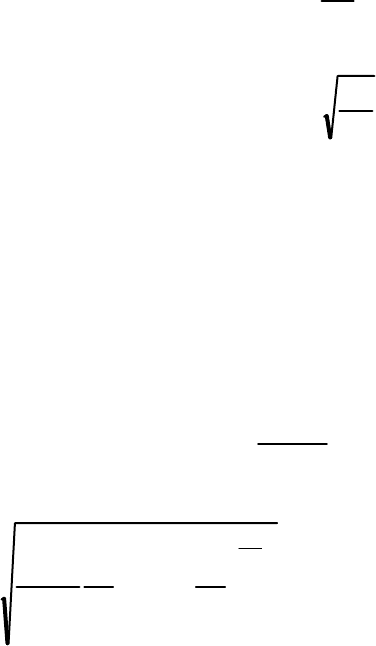
10
Площадь поперечного сечения сопла и диаметр определим по
формулам:
w
G
F
ρ
&
= , (1.23)
π
F
D
4
=
. (1.24)
Численное решение системы уравнений (1.22)-(1.24) реализовано в
программе “LAV1A” (см. приложение №1).
Так как точность расчета, выполненного численным методом, зависит от
величины выбранного шага по продольной координате Δ
x, то можно найти
такой шаг, который обеспечит расчет с заданной относительной погрешностью
100⋅
−
=
s
s
w
ww
ε
, (1.25)
где
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
=
−
k
k
s
p
p
T
R
k
k
w
1
*
0
*
1
0
1
)1(
2
μ
- изоэнтропийная скорость.
Для выполненного методом Рунге-Кутта расчета (
&
G
=0,3 кг/с; l=0,15 м;
w
0
=30 м/с; T
0
=426 K; p
0
=0,6 MПа; p
ср
=0,1 МПа; k=1,4; см. программу
“LAV1A”) при шаге Δ
x=0,3⋅10
-3
м относительная погрешность в сечении
x=0,3⋅10
-3
м составила
ε
= -1,74 %, а на выходе сопла -3,51⋅10
-2
%, то есть
(
w
s
-w)=-0,206 м/с, что свидетельствует о высокой точности расчета.
Проверка достоверности численного расчета проводилась путем
сравнения с расчетом сопла с помощью интегральных соотношений.
Проведенное тестирование подтверждает корректность метода, что позволяет
выполнять численные расчеты течения в каналах, работающих на двухфазных
потоках, когда отсутствуют аналитические решения.
Рассмотрим течение идеального газа при наличии
сил трения. В этом
случае уравнение движения примет вид:
DdxFdpdwG
W
πτ
−−=
&
, (1.26)
где
τ
W
=c
f
ρ
w
2
/2 - касательное напряжение на стенке канала. Разрешая (1.26)
относительно
dw/dx, получим

11
D
wc
dx
dp
wdx
dw
f
2
1
−−=
ρ
. (1.27)
Теперь система уравнений для прямой задачи запишется в виде:
()
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
−
=
−
−
−=
−−=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−−+
−
=
.
)1(
,
)1(
)1(
,
2
1
,
1
)1(1
2
)1(
2
2
2
2
2
2
2
dx
dF
F
M
M
dx
d
dx
dF
F
TM
M
k
dx
dT
D
wc
dx
dp
wdx
dw
dx
dF
F
Mk
D
c
M
pkM
dx
dp
f
f
ρρ
ρ
(1.28)
Численное решение системы (1.28) при
F=f(x) приведено в программе
“LAV1T”(см. приложение №1).
2. Модель гомогенного потока
Экспериментальные исследования показывают, что при течении в каналах
вскипающих потоков (когда в канал поступает жидкость по своим свойствам
близкая к состоянию насыщения) или высоковлажных потоков при высоких
начальных давлениях (
p
0
*
>3 МПа) и значительных градиентах давления вдоль
канала, можно в первом приближении использовать для расчетов теорию
гомогенного потока [4], когда текущую среду наделяют свойствами “тумана”,
где отсутствует раздел между фазами, а сами фазы находятся в механическом
итермическом равновесии. Возникает необходимость в исследовании поведения
таких потоков в каналах переменного сечения.
Туманообразная изотропная среда
может рассматриваться как континуум
и характеризоваться обычными макровеличинами - термодинамическими
параметрами (
p,T,v,i,s). В такой среде внешнее воздействие не нарушает
теплового и механического равновесия между фазами. Считают, что скорость
звука в такой бесконечной изотропной среде определяется по формуле Лапласа
S
S
pa )(
∂ρ∂
=
. (2.1)
Найдем выражение для термодинамической скорости звука в такой среде.
Запишем первый закон термодинамики для обратимого процесса
dq=du+pdv , (2.2)
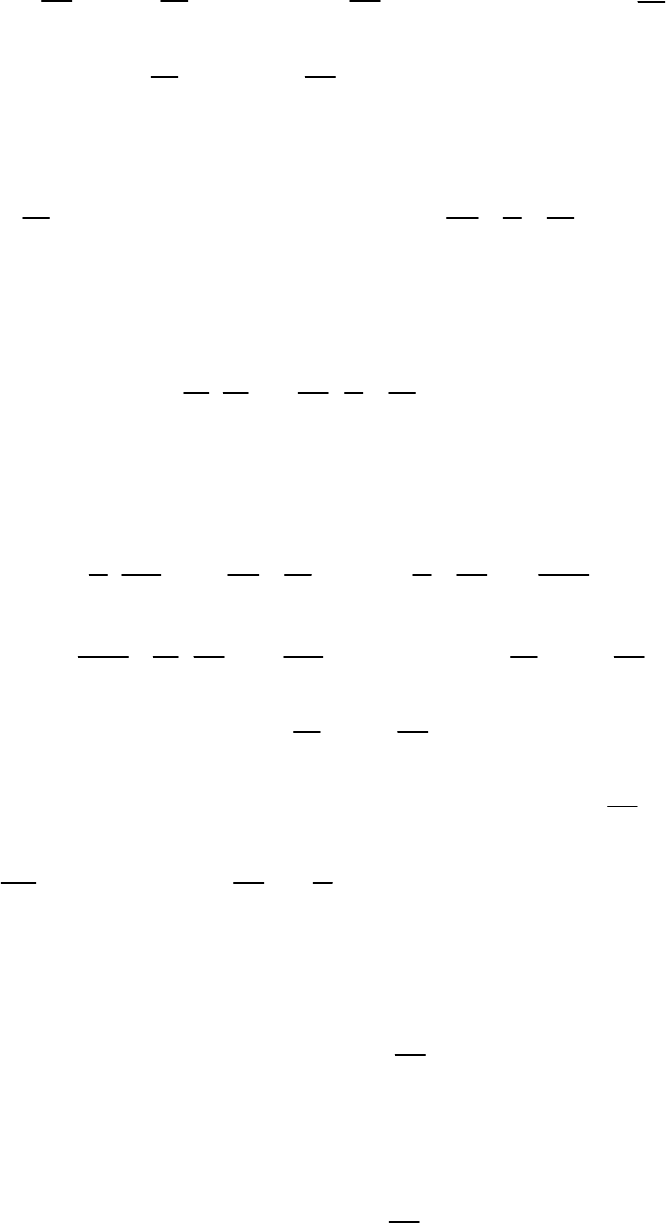
12
но
dv
v
u
dT
T
u
du
Tv
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=
∂
∂
∂
∂
, a
v
v
T
u
c
⎟
⎠
⎞
⎜
⎝
⎛
=
∂
∂
, тогда
dvp
v
u
dTcdq
T
v
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
+=
∂
∂
.
Покажем, что
v
T
T
p
Tp
v
u
⎟
⎠
⎞
⎜
⎝
⎛
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
.
Из объединенного закона термодинамики для обратимого процесса,
записанного в виде
dvp
v
u
dTcTds
T
v
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
+=
∂
∂
следует
dvp
v
u
TT
dT
cds
T
v
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
+=
∂
∂
1
. Поскольку
энтропия, как функция состояния, является функцией двух переменных
Т и v, то
накрест взятые производные должны быть равны:
v
T
T
v
p
v
u
TTT
c
v
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
=
⎥
⎦
⎤
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
1
Взяв производные от левой и правой частей, получим
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎥
⎦
⎤
⎢
⎣
⎡
vT
u
T
p
T
p
v
u
T
v
c
T
V
T
T
V
∂∂
∂
∂
∂
∂
∂
∂
∂
2
2
111
,
но
T
V
v
v
c
T
u
vvT
u
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
∂
∂
∂
∂
∂
∂
∂∂
∂
2
, тогда
v
T
T
p
T
v
u
p
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∂
∂
∂
∂
.
Отметим, что выражение
p
T
p
T
v
u
v
T
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
называют калорическим
уравнением состояния реального газа. Для идеального газа
∂
∂
u
v
T
⎛
⎝
⎜
⎞
⎠
⎟
= 0
, и имеем
тождество
0=− p
v
RT
, так как
v
R
T
p
v
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
.
Таким образом, первый закон термодинамики для обратимого процесса может
быть записан в виде
dv
T
p
TdTcdq
v
v
⎟
⎠
⎞
⎜
⎝
⎛
+=
∂
∂
. (2.4)
Теперь для политропического процесса можно написать
()
0=
⎟
⎠
⎞
⎜
⎝
⎛
+− dv
T
p
TdTcc
v
nv
∂
∂
, (2.5)
где
dq=c
n
dT; c
n
- удельная теплоемкость политропического процесса.
Так как
T=
ϕ
(p,v), то
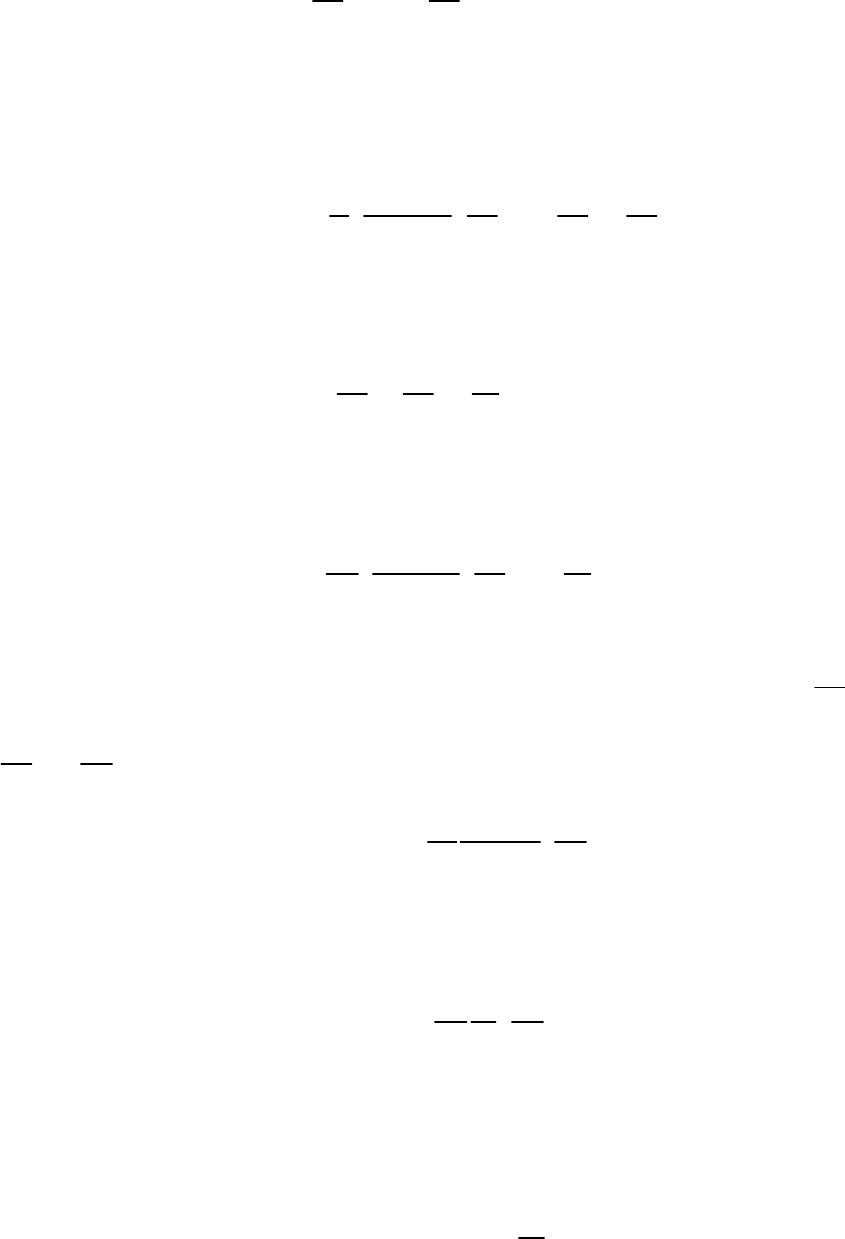
13
dp
p
T
dv
v
T
dT
v
p
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=
∂
∂
∂
∂
. (2.6)
Введем понятие характеристической скорости звука [4]
a
2
=dp/d
ρ
. (2.7)
С учетом (2.5) и (2.6) преобразуем (2.7) к виду
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
=
v
p
v
nv
T
p
v
T
T
p
cc
T
a
∂
∂
∂
∂
∂
∂
ρ
2
2
)(
1
. (2.8)
Используя известную связь между производными
1−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
T
p
v
p
v
v
T
T
p
∂
∂
∂
∂
∂
∂
, (2.9)
уравнение (2.8) представим в форме
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
=
Tv
nv
v
p
T
p
cc
T
a
∂
∂
∂
∂
ρ
2
2
2
)(
1
. (2.10)
Для однокомпонентной двухфазной области
p=f(T), следовательно
∂
∂
p
v
T
⎛
⎝
⎜
⎞
⎠
⎟
= 0
, а
dT
dp
T
p
v
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
, тогда
2
2
2
)(
1
⎟
⎠
⎞
⎜
⎝
⎛
−
=
dT
dp
cc
T
a
nv
ρ
. (2.11)
Если вещество в звуковой волне не обменивается теплотой с окружающей
средой, то
с
n
=0, а выражение (2.11) переходит в формулу Кёртиса
2
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
=
dT
dp
c
T
a
v
s
ρ
. (2.12)
Разделив (2.11) на (2.12), получим связь между характеристической и
термодинамической скоростями звука
1
22
1
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
v
n
s
c
c
aa
. (2.13)
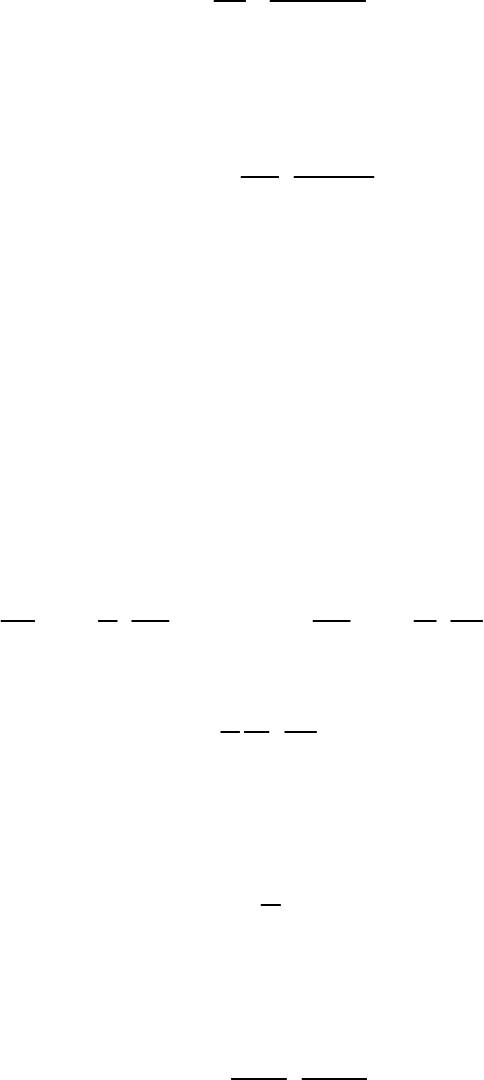
14
Таким образом, в потоках с интенсивным подводом и отводом теплоты
кризисная ситуация возникает при
w=a , а в адиабатических потоках при w=a
s
.
С учетом уравнения Клапейрона-Клаузиуса
)( vvT
r
dT
dp
′
−
′′
=
, (2.14)
перепишем (2.12) в более удобной для расчетов форме
2
2
)(
1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
′
−
′′
=
vv
rv
Tc
a
v
S
, (2.15)
где
cxcxc
vvvvv
=−
′
+
′′
()1
- удельная изохорная теплоемкость влажного пара; c
v
'
и
c
v
"
-удельные теплоемкости насыщенной жидкости и сухого насыщенного
пара со стороны двухфазной области [5];
v=(1-x
v
)v
'
+x
v
v
"
- удельный объем
влажного пара. Из (2.15) видим, что термодинамическая скорость звука в
гомогенном потоке зависит не только от температуры, как в идеальном газе, но
и от степени сухости.
Найдем связь между термодинамической скоростью звука и показателем
изоэнтропы во влажном паре.
По определению
ss
v
p
p
v
u
i
k
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∂
∂
∂
∂
, но
2
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
dT
dp
c
T
v
p
v
s
∂
∂
, тогда
2
⎟
⎠
⎞
⎜
⎝
⎛
=
dT
dp
c
T
p
v
k
v
. (2.16)
Сравнивая (2.12) и (2.16), находим, что
kpv
p
k
s
a ==
ρ
2
. (2.17)
Вместо (2.16) можно написать
2
⎟
⎠
⎞
⎜
⎝
⎛
′
−
′′
=
vv
r
pTc
v
k
v
. (2.18)
Из формул видно, что в двухфазной области показатель изоэнтропы
является переменной величиной. Напомним, что для идеального газа
k=(
∂
i/
∂
u)
s
=c
p
/c
v
.
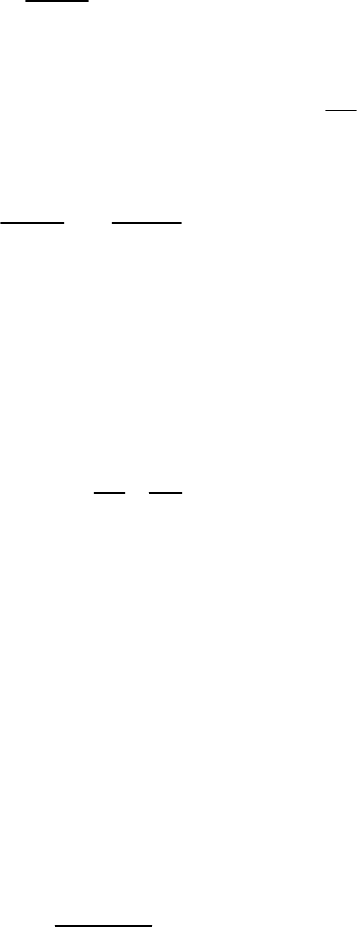
15
Так как в современном энергомашиностроении имеют место, как
правило, критические и сверхкритические режимы течения, то необходимо
установить условия существования этих режимов. Если считать, что кризис
течения характеризуется независимостью плотности тока от давления, то
можно написать
(
)
0=
⎥
⎦
⎤
⎢
⎣
⎡
s
p
w
∂
ρ∂
. (2.19)
Раскрывая (2.19) с учетом уравнения Бернулли
wdw
dp
p
=−
, получим
()
0
1
2
=
−
=
⎥
⎦
⎤
⎢
⎣
⎡
w
M
p
w
s
∂
ρ∂
. (2.20)
Таким образом, в гомогенном изоэнтропийном потоке, как и в потоке
идеального газа, кризис течения имеет место при
M=1. Здесь также для
получения сверхзвуковых потоков необходимо применять каналы, имеющие
суживающуюся и расширяющуюся части
()
F
dF
w
dw
M =−
1
2
. (2.21)
Кризис течения имеет место в наименьшем сечении канала, то есть при
dF=0, в
этом сечении поток имеет наибольшую плотность тока
()
max
ww
ρ
ρ
=
.
Рассмотрим изоэнтропийное течение одномерного гомогенного потока в
канале переменного сечения. Для его описания необходимо иметь четыре
уравнения: сплошности, движения, энергии и Клапейрона-Клаузиуса,
устанавливающего связь между температурой и давлением насыщения.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
′
−
′′
−
=+
=+
=
,0
)(
,0
,0
,0)/(
dT
vvT
r
dp
wdwdi
vdpwdw
vwFd
(2.22)
где
i=f(p,v).
Перепишем (2.22) в виде
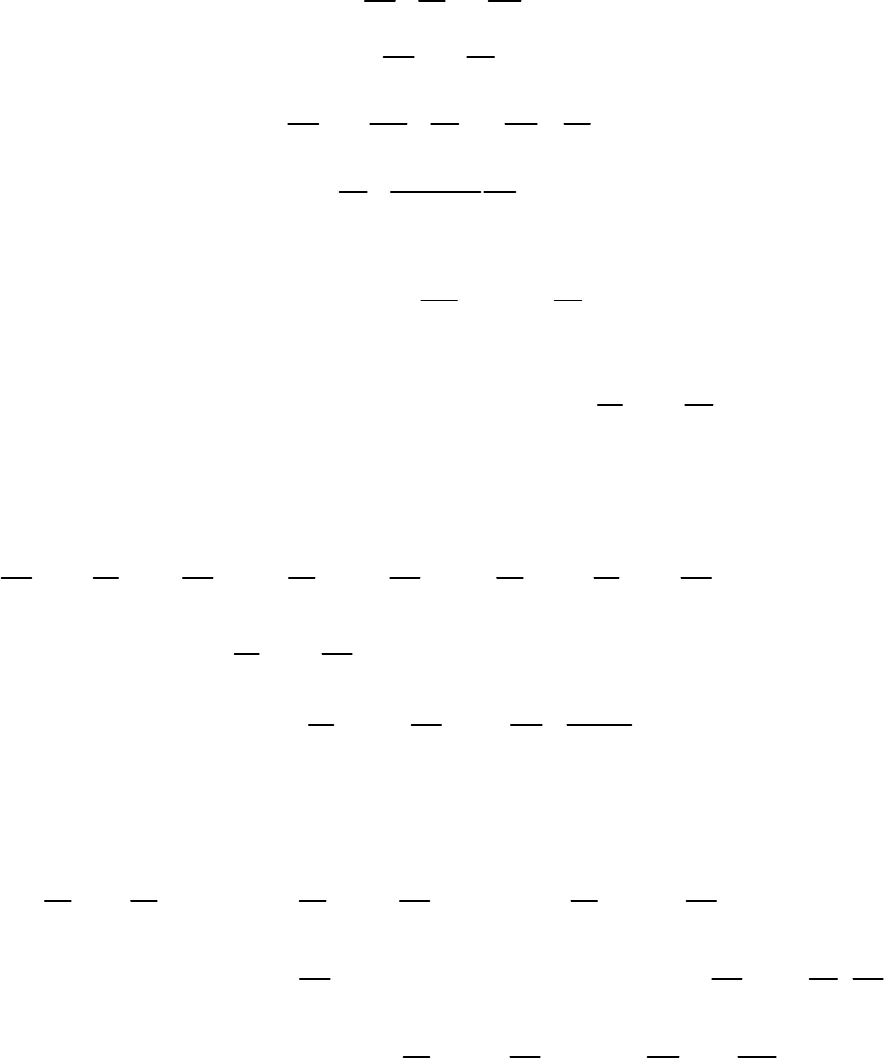
16
()
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
=
′
−
′′
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=+
−=−
0
,0
,0
,
2
2
T
dT
pvv
r
p
dp
v
dv
v
i
v
p
dp
p
i
p
w
dw
w
p
dp
pv
w
dw
w
F
dF
v
dv
w
dw
pv
∂
∂
∂
∂
(2.23)
Выразим частные производные
V
p
i
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
и
P
v
i
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
через термодинамические
параметры. Запишем объединенный закон термодинамики для обратимого
процесса в виде
Tds=di-vdp . При р=const
PP
v
i
v
s
T
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
. Воспользуемся
уравнениями Максвелла, устанавливающими связь между частными
производными термодинамических функций в различных процессах
P
S
s
v
p
T
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
,
v
S
p
s
T
v
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
,
T
P
p
s
T
v
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
,
v
T
p
T
s
v
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
.
Для нашего случая
S
P
T
p
v
s
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
, тогда
vv
r
dT
dp
T
T
p
T
v
i
S
p
′
−
′′
==
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
.
Дифференцируя уравнение
Tds=di-vdp по давлению при v=const ,
получим
v
p
i
p
s
T
vv
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
, но
S
v
T
v
p
s
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
, тогда
v
T
v
T
p
i
S
v
+
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
. Используя
уравнение
dv
T
p
TdTcTds
v
V
⎟
⎠
⎞
⎜
⎝
⎛
+=
∂
∂
при s=const, будем иметь
v
V
S
p
T
T
c
T
v
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
, с
учетом чего можно написать
()
vvv
r
Tc
v
dp
dT
cv
p
T
c
p
i
v
v
v
v
v
+
′
−
′′
=+=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
.
Составим главный определитель системы (2.23)

17
()
()
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
′
−
′′
−=
′
−
′′
−
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=Δ v
p
i
w
v
i
v
vv
r
pvv
r
v
i
v
p
i
pw
pvw
v
p
p
v
∂
∂
∂
∂
∂
∂
∂
∂
22
2
2
010
0
00
1001
() ()
()()
2
2222
2
1
⎟
⎠
⎞
⎜
⎝
⎛
′
−
′′
−=−
′
−
′′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
′
−
′′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
vv
vr
Mwa
vv
v
p
i
r
w
v
p
i
v
i
v
vv
v
p
i
r
s
v
v
p
v
∂
∂
∂
∂
∂
∂
∂
∂
(2.24)
или Δ=(
M
2
-1)c
v
Ta
s
2
, где
2
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
′
−
′′
=
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
=
vv
vr
Tc
v
p
i
v
i
v
a
v
v
p
s
∂
∂
∂
∂
.
Выполнив операции по нахождению определителей искомых величин,
получим:
()
()
()
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
′
−
′′
=Δ
⎟
⎠
⎞
⎜
⎝
⎛
−=Δ
⎟
⎠
⎞
⎜
⎝
⎛
′
−
′′
−=Δ
⎟
⎠
⎞
⎜
⎝
⎛
′
−
′′
=Δ
.
,
,
,
2
2
2
2
F
dF
v
p
i
pw
pvv
r
F
dF
v
i
vw
F
dF
v
i
pvv
rvw
F
dF
v
i
vv
rv
v
v
p
T
p
p
p
w
∂
∂
∂
∂
∂
∂
∂
∂
(2.25)
Используя формулу Крамера, найдем производные для решения прямой
задачи
()
()
()
()
()
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
−
=
Δ
Δ
=
−
′
−
′′
−=
Δ
Δ
=
−
−=
Δ
Δ
=
−
=
Δ
Δ
=
.
1
,
1
,
1
1
,
1
1
2
2
2
2
2
2
2
dx
dF
FM
vM
dx
dv
dx
dF
rvFM
Twvv
dx
dT
dx
dF
vF
w
M
dx
dp
dx
dF
F
w
M
dx
dw
v
T
p
w
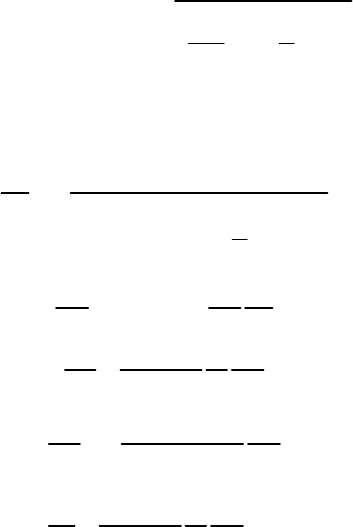
(2.26)
Для обратной задачи, когда, например,
18
11
2
0
0
+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
l
x
p
p
p
p
cp
,
система уравнений примет вид:
(
)
()
()
()
()
()
()
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
−
=
−
′
−
′′
−=
−
=
−−=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−=
.
1
,
1
,
1
1
,1
,
11/
1/2
2
2
2
2
2
2
2
2
2
0
2
0
dx
dF
F
v
M
M
dx
dv
dx
dF
rvFM
wvvT
dx
dT
dx
dF
F
w
M
dx
dw
dx
dp
w
vF
M
dx
dF
l
x
ppl
xppp
dx
dp
cp
cpo
(2.27)
Численное решение системы уравнений (2.26) реализовано в программах
GM1A и GM4, а системы (2.27) - GM2 и GM3 (см. приложениe №2).
Во всех программах начальная степень сухости пара
(
)
wvvv
GGGx
&&&
+= /
может изменяться от 0,05 до 1, что делает их универсальными, так как это
позволяет выполнять расчеты равновесного расширения высоковлажного пара
и сухого насыщенного пара.
В программах GM1A и GM2 физические свойства воды и пара на линии
насыщения представлены оператор-функциями. В программах GM3 и GM4
используются подпрограммы “SPLINE” и “SEVAL”. Первая позволяет найти
коэффициенты полинома, аппроксимирующего функцию, вторая
- значение
искомой величины в заданной точке. В программах GM1A и GM2 необходимо
знать или получить аналитические зависимости свойств вещества от
температуры, например,
v
′
=f(T), v
″
=f
1
(T), r=
ϕ
(T), c
v
′
=
ϕ
1
(T), c
v
″
=
ϕ
2
(T), и т.д. В
GM3 и GM4 достаточно лишь занести табличные значения физических величин
в файл данных, что является несомненным преимуществом этих программ.
Однако число строк в программе при этом увеличивается.
В реальных системах поток кроме геометрического воздействия
L
1
=(1/F)(dF/dx) испытывает силовое воздействие, обусловленное трением
L
2
=-2c
f
w
2
/D и может подвергаться тепловому L
3
=-4q
w
v/(wD)=-4
α
v(T-T
w
)/(wD) и
химическому воздействию
L
4
. В дальнейшем будем считать, что L
4
=0.
В этом случае уравнения движения и энергии принимают вид:
).,(где,
,
*
pvfiDdxqdiG
DdxFdpdwG
w
w
==
−−=
π
πτ
&
&
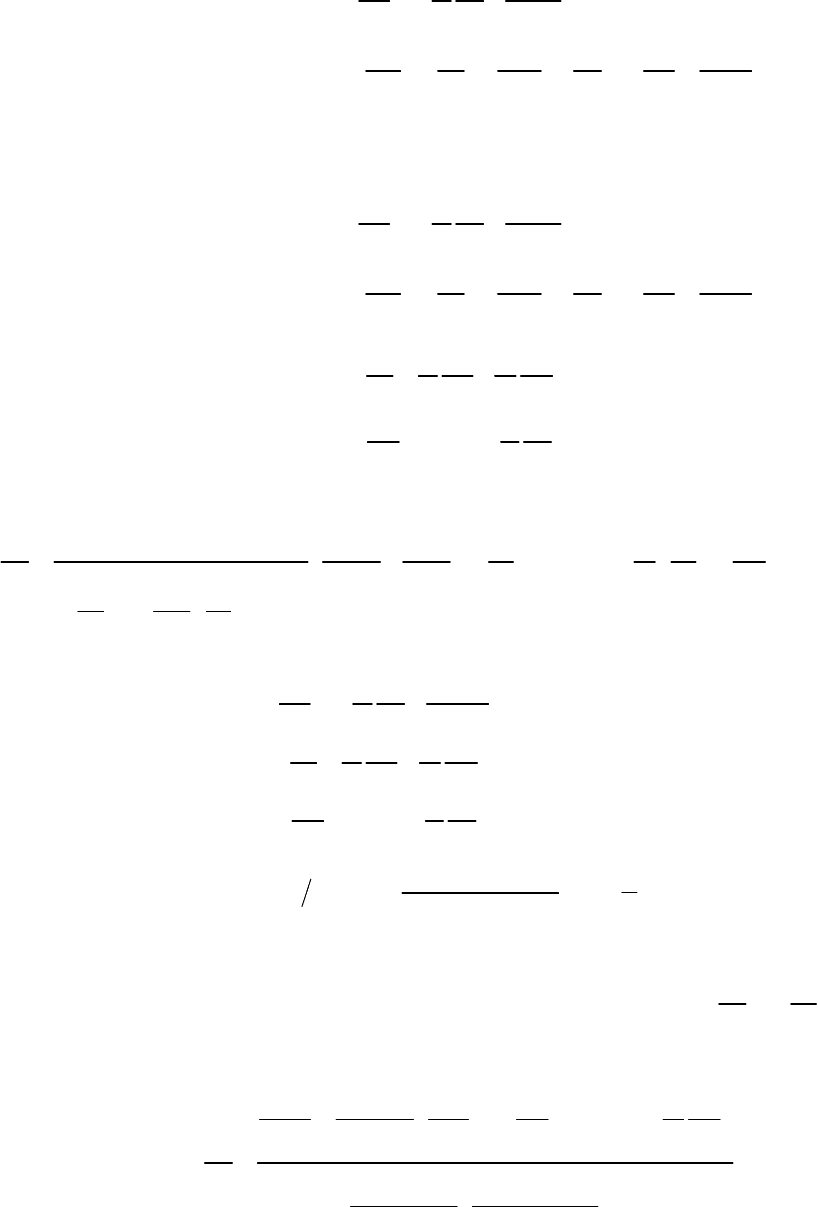
19
После преобразования этих уравнений будем иметь:
D
wc
dx
dp
w
v
dx
dw
f
2
−−=
,
wD
vq
dx
dw
w
dx
dp
v
p
i
dx
dv
p
v
i
w
4
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
.
Теперь вместе с уравнениями сплошности и Клапейрона-Клаузиуса
система уравнений примет вид:
D
wc
dx
dp
w
v
dx
dw
f
2
−−=
,
wD
vq
dx
dw
w
dx
dp
v
p
i
dx
dv
p
v
i
w
4
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
,
dx
dF
F
v
dx
dw
w
v
dx
dv
−=
,
()
dx
dp
r
T
vv
dx
dT
′
−
′′
=
.
Разрешая систему относительно
dp/dx, получим
()
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
′
−
′′
=
+=
−−=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
,
,
,
2
2
2
4
2
2
1
dx
dp
r
T
vv
dx
dT
dx
dF
F
v
dx
dw
w
v
dx
dv
D
w
f
c
dx
dp
w
v
dx
dw
dx
dF
p
v
i
F
v
w
p
v
i
v
D
f
c
wD
v
w
q
v
p
v
i
w
v
v
p
i
dx
dp
∂
∂
∂
∂
∂
∂
∂
∂
(2.28)
где
cf
f
= (Re) ;
Re
=
wD
ρ
μ
;
μμ
μ
μ
μ
′′
−+
′
′
′
′
=
)1(
vv
xx
,
v
1
=
ρ
,
vxvxv
vv
′′
+
′
−
=
)1(
, где x
v
–
степень сухости пара.
Подставляя в
dp/dx выражения частных производных
p
v
v
i
p
i
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
,
найдем,
что
()
()
()
()
()
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
′
−
′′
′
−
′′
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
′
−
′′
+
′
−
′′
+
=
1
1
1
2
4
2
2
2
2
2
vr
vvTc
wvv
rv
dx
dF
F
vv
vr
w
D
c
vv
rv
wD
vq
dx
dp
v
f
w
. (2.29)
Используя формулу для термодинамической скорости звука (2.15), перепишем
(2.29) в виде
