Baggott J. The Quantum Story: A History in 40 Moments

Подождите немного. Документ загружается.

the quantum story

240

considered as a solid ‘ball’ of material substance, with mass and charge

distributed evenly, much like snow and ice is distributed in a snowball.

Or it could be thought of as a region of largely empty space containing

discrete, point-like charged constituents. High-energy electrons encoun-

tering such point-like constituents could be expected to be scattered in

greater numbers and at larger angles.

Bjorken found that, for these different conceptions of the proton struc-

ture, the theory predicted quite different results in the region of deep

inelastic collisions. He realized that an experimental test was possible,

comparable in many ways to the Geiger–Marsden experiments which

supported the view that the mass of an atom is concentrated in a small

positively charged nucleus. Just as the scattering of alpha-particles from

their target gold atoms revealed the interior structure of the atom, so the

observations of electrons scattered from target protons would reveal the

interior structure of the proton.

Bjorken speculated that such point-like constituents might be quarks

and performed some calculations for the spectrum of scattered electron

energies that would result. But his heart wasn’t yet in it. The quark model

was still treated with derision by the physics community and there were

alternative theories available that were better regarded. He quickly

backed off from proposing that these experiments could be used as a

test of the quark model. ‘I brought it in mainly as a desperate attempt

to interpret the rather striking phenomenon of point-like behaviour,’ he

explained when challenged on this view at a conference held at Stanford

in September 1967.

Studies of deep inelastic scattering at relatively small angles from a

liquid-hydrogen target began at SLAC around this time and continued

through October 1967. They were carried out by a small experimental

group including MIT physicists Jerome Friedman and Henry Kendall and

Canadian-born SLAC physicist Richard Taylor. The experiments did not

initially go smoothly.

The analysis programs had to be rewritten as we continued to test the

workings of the spectrometer hardware. After a couple of weeks of total

chaos, things began to settle down. We took a full set of data at 6° with sev-

eral initial energies and with scattered electron energies down to 2–3 GeV.

deep inelastic scattering

241

The raw data had to be corrected for all the radiative processes involving

the swarm of virtual particles surrounding the electron. Although these

corrections were signiﬁ cant, accounting for up to half of the measure-

ments recorded in the SLAC experiments, they could be handled satisfac-

torily using quantum electrodynamics.

Even at the relatively low scattering angles of 6° and 10°, the physicists

observed many more scattered electrons than they had anticipated. They

focused their attention on the behaviour of something called the ‘struc-

ture function’ as a function of the difference between the initial electron

energy and the scattered electron energy. This difference is related to the

energy lost by the electron in the collision or the energy of the virtual

photon that is exchanged. They saw that as the virtual photon energy

was increased, the structure function showed marked peaks correspond-

ing to the expected proton resonances. However, as the energy increased

further, these peaks gave way to a broad, featureless plateau that fell away

gradually as it extended well into the range of deep inelastic collisions.

Bjorken had anticipated something like this. It was indeed the signa-

ture of point-like proton constituents. He made a further suggestion.

If the structure function declined gradually with increasing energy of

the virtual photon, then the product of these (called F), plotted against

the photon energy (or frequency, n) divided by the square of something

called the four-momentum transfer (q

), might show some interesting

behaviour.

Kendall drew the graph by hand, using two sheets of orange graph

paper that had been taped together. It showed F increasing to a maxi-

mum for n/q

around 3 GeV, and remaining fairly constant thereafter.

Bjorken called it ‘scaling’. The curve was the same irrespective of the

electron energy. The mathematics said it had to be this way, but it was

not at all clear what this meant.

Irrespective of what it meant, Kendall was struck by the way the

experimental data had so closely conformed to Bjorken’s predictions.

Years later he recalled ‘. . . wondering how Balmer may have felt when

he saw, for the ﬁ rst time, the striking agreement of the formula that

The four-momentum transfer is calculated from the initial and ﬁ nal electron energies and

the scattering angle.

the quantum story

242

bears his name with the measured wavelengths of the atomic spectra

of hydrogen.’

There was as yet no rush to embrace these experimental results as

proof of the existence of an internal structure for the proton, and cer-

tainly no rush to declare the results as evidence for the existence of

quarks. There were other possible theoretical explanations for the scat-

tering results and for the phenomenon of scaling, and arguments broke

out even within the MIT-SLAC group. Nevertheless, on Kendall’s insist-

ence the graph that Bjorken had suggested was included in a paper on the

group’s results presented at a conference in Vienna in August 1968.

Richard Feynman had collected a Nobel Prize in December 1965 for his

contribution to the development of quantum electrodynamics, alongside

Julian Schwinger and Sin-Itiro Tomonaga. In the years that followed he had

adapted to the celebrity status it afforded, but had at the same time lost touch

with contemporary high-energy physics. He had helped resolve some of the

0.5

0.4

6° 16 GeV

6° 13.5 GeV

6° 10 GeV

0.3

0.2

0.1

F =Frequency x Structure Function

0.0

01 2 3 4 5 6 7

Frequency/Four-momentum Transfer (per GeV)

fig 15 Prompted by suggestions by Bjorken, Kendall drew up this graph by hand.

The shape of the resulting curve was the same irrespective of the electron energy (in

this case, 10, 13.5 and 16 GeV, with a scattering angle of 6°). Bjorken called it ‘scaling’. It

was the tell-tale signature of point-like constituents inside the proton. Adapted from

Michael Riordan, The Hunting of the Quark: A True Story of Modern Physics, Simon &

Shuster, New York, 1987, p. 146.

deep inelastic scattering

243

problems of QED and, with Gell-Mann, had made important contributions

to the theory of the weak force. But the strong force had eluded him.

He had resolved to play catch-up. In June 1968 he developed an out-

line of a theory of the hadrons in which he imagined them to consist of

point-like constituents which, for want of a better name, he had dubbed

partons, meaning simply the ‘parts’ of hadrons. The parton model was not

grounded in a detailed quantum ﬁ eld theory, it was simply an idea he was

toying with. What he wanted to know was that if the hadrons could be

thought to be composed of partons, what were the consequences?

He had also developed an image in his mind of two hadrons colliding

together. At high speeds, special relativity says that each hadron ‘sees’ the

other not as a fully ﬂ eshed-out three-dimensional object but rather as a

two-dimensional ﬂ at pancake. If these pancakes were dotted with tiny,

hard partons, then a hadron–hadron collision would really be the sum of

a series of individual collisions between the constituent partons.

Feynman’s sister Joan lived in a house just across the road from SLAC,

and during visits to her he would take the opportunity to ‘snoop around’

the facility. He would chat to the physicists at a picnic table in the shade

of the oak trees near the SLAC cafeteria, regaling them with stories from

his Los Alamos days. He would also listen carefully as they told him

about the latest developments in high-energy physics.

In August 1968 he heard about the work of the MIT-SLAC group on

deep inelastic scattering. A second round of experiments was about to

begin, but the physicists were still puzzling over the interpretation of the

data from the previous year. Bjorken was out of town, but his new post-

doctoral student Emmanuel Paschos told Feynman about scaling and

asked him what he thought.

When Feynman saw Kendall’s graph he collapsed to his knees, his

hands raised to the heavens. ‘All my life,’ he exclaimed, ‘I’ve looked for an

experiment like this, one that can test a ﬁ eld theory of the strong force!’

Feynman knew that the graph was telling him something, but he was

not quite sure what it was. He ﬁ gured it out that night in his motel room.

The graph was related to the distribution of momentum of the point-like

constituents—the partons—in the proton. In fact, simply by inverting

the function that Kendall had plotted along the horizontal axis (in other

words, by plotting q

/n), the graph became a probability distribution,

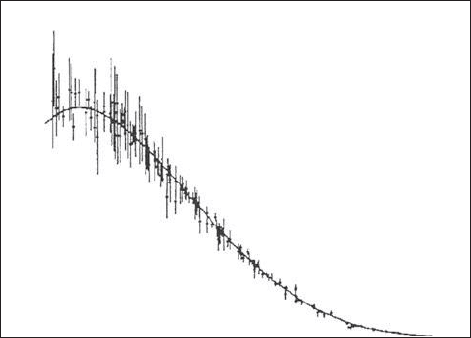
the quantum story

244

each point a measure of the probability of the electron colliding with a

parton carrying a speciﬁ c fraction of the total momentum of the proton.

This could be pushed a little further. When divided by the proton mass,

the quantity q

/n is related to the fraction of the proton mass carried by

the parton.

‘I’ve really got something to show youse guys,’ Feynman declared to

Friedman and Kendall the next morning, ‘I ﬁ ggered it all out in my motel

room last night!’ This was followed by much enthusiastic arm-waving.

Bjorken had arrived at most of the conclusions that Feynman had now

drawn, but Bjorken had expressed them in the esoteric language of current

algebra. When he had had a chance to read Bjorken’s papers, Feynman

acknowledged his priority. But, once again, Feynman was describing the

events in a far simpler, yet richer, more visual way. When he returned to

SLAC in October 1968 to deliver a lecture on the parton model, it was

like setting a ﬁ re. Suddenly, all the talk among SLAC physicists was of

0.5

0.4

0.3

0.2

0.1

F = Frequency x Structure Function

0.0

Parton Mass Fraction

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

fig 16 Feynman ﬁ gured that he could re-plot Kendall’s graph in terms of the frac-

tion of the proton mass carried by the point-like constituents, which he called ‘par-

tons’. The result would be a distribution of the probability for the electron colliding

with a parton carrying a speciﬁ c fraction of the proton’s total momentum. Adapted

from Michael Riordan, The Hunting of the Quark: A True Story of Modern Physics, Simon

& Shuster, New York, 1987, p. 152.

deep inelastic scattering

245

partons. Nothing is more guaranteed to breed conﬁ dence in a bold idea

than its enthusiastic reception by a Nobel Laureate.

Were partons actually quarks? Feynman didn’t know and didn’t care. Some

of the SLAC theorists developed models in which the partons were pions and

protons, stripped of their clouds of virtual particles. But Bjorken and Paschos

soon had a detailed model of partons based on a triplet of quarks.

Further experiments at scattering angles of 18°, 26°, and 34° conﬁ rmed

the original impressions and reproduced the scaling behaviour. By 1970

experiments had been performed using a liquid-deuterium target. By

carefully separating the contributions to scattering from the proton, it

was possible to determine the equivalent structure function for the neu-

tron and so probe its interior structure in the same way.

These were difﬁ cult experiments, and it was not all plain sailing. One

theoretical model describing collisions between electrons and protons and

electrons and neutrons suggested that the extent of deep inelastic scattering

should depend on the relative strengths of the electric charges of the parton

constituents. If the partons were considered to be quarks, then the ratio of

scattering events for the neutron versus the proton should be given as the

ratio of the sum of the squares of the charges of their quarks constituents.

For the neutron, thought to consist of an up quark and two down quarks

(udd), the sum of the squares of the fractional charges is

⁄

. For the

proton, consisting of two up quarks and a down quark (uud), the sum is

⁄

or 1. The ratio of neutron versus proton scattering events (N/P), was there-

fore expected to fall with increasing q

/n to a limiting value of

⁄

Early results appeared to be consistent with this simple model. But as

/n increased, the ratio N/P was discovered to fall substantially below

⁄

These results ruled out a variety of competing theories, but seemed also

to tell against the model of fractionally charged quarks.

Theorists had a ﬁ eld day trying to rationalize these results with exist-

ing models. There was still some hope for quarks, however. The model

that predicted a limiting value of N/P of

⁄

was rather naïve. It assumed

that the momentum of the nucleon was evenly distributed over the three

quark constituents. There were other models in which the three quarks

which characterize the nucleon (called ‘valence’ quarks) swim in a ‘sea’ of

quark–anti-quark pairs.

the quantum story

246

In addition, the quarks (or, more generally, partons) were now thought

to be bound together through the exchange of strong force ﬁ eld particles

called gluons, the ‘glue’ that holds the ‘parts’ together. These short-range

force particles were required to be massive. So, the momentum of the

nucleons may be shared among quark–anti-quark pairs and gluons, and

is in any case not necessarily obliged to be shared equally among the

valence quarks. It was recognized that N/P could indeed fall below

⁄

But it could not fall below a lower limit of ¼, in which only a down quark

from the neutron and an up quark from the proton contribute to the

scattering.

When experimental results suggested that the ratio actually did fall

below ¼, both Bjorken and Feynman insisted that no further modiﬁ ca-

tions could save the quark theory. If the results were right, then the par-

tons simply could not be fractionally charged quarks.

The results were wrong. An error was discovered in the computer

program used to correct for the effects of ‘smearing’ due to the inter-

nal motions of the protons and neutrons in the hydrogen and deuterium

target atoms. When this error was removed, the ratio of N/P was seen to

fall to a limiting value close to ¼.

Earlier experimental studies had revealed that the partons were spin-½

fermions. The N/P data now strongly supported the idea of fractional

charges. Experimental results from studies of deep inelastic scattering of

neutrinos from protons at CERN provided further supporting evidence.

By mid-1973, quarks had ofﬁ cially ‘arrived’. They might have been con-

ceived partly in jest as a strange quirk of nature, but they had now taken

a decisive step towards acceptance as real constituents of the hadrons.

Some questions remained unanswered. If 20-GeV electrons were strik-

ing fractionally charged quarks inside protons or neutrons, resulting in

the destruction of the target nucleons, how come no free quarks had ever

been seen? More worrying, perhaps, was the fact that the quarks inside

the proton and neutron behaved as though they were largely independ-

ent of each other. The phenomenon of scaling suggested that the quarks

could be considered to roam freely inside the nucleons.

How was this possible? Surely, the strong force must keep the quarks

tightly bound inside the nucleons; so tightly bound that they are forever

conﬁ ned?

247

The SLAC results on deep inelastic scattering of electrons from protons were still inter-

preted with some caution. There were many questions that remained unanswered. But, for

the advocates of the quark model, here was the ﬁ rst evidence that these ultimate constitu-

ents of matter might actually be real.

Sheldon Glashow was an early convert to the quark model. In fact, based on little more

than an appeal to an essential tidiness in nature, he had speculated with James Bjorken in

1964 that there should be a fourth quark, which they had called charm. At that time the

four leptons—electron, electron neutrino, muon, and muon neutrino—seemed at odds

with just three quarks—up, down, and strange. A fourth quark was surely needed to even

things up.

Glashow had collaborated with Bjorken whilst visiting the Niels Bohr Institute in

Copenhagen. For Bjorken, this was an unusual line of reasoning. More used to anticipat-

ing the properties and behaviour of particles likely to have implications for experiment,

this was for him, at best, a highly speculative proposal. ‘You have to remember the ﬂ a-

vour of the time,’ he explained, ‘It was an easygoing time for models. Models came and

went.’ He was nevertheless rather ambivalent about the proposal. Instead of using his own

name, James Daniel Bjorken, he signed the paper ‘B.J. Bjørken’, using his nickname, ‘BJ’,

and a Danish interpretation of his originally Swedish surname.

Glashow’s attempts to build an SU(2) × U(1) ﬁ eld theory of the weak and electromag-

netic forces had foundered on the problem of the Z

boson and the weak neutral currents it

implied. With Bjorken he had actually arrived at the solution to this problem, but he had

Of Charm and Weak

Neutral Currents

Harvard, February 1970

the quantum story

248

failed to make the connection. It seems that Glashow had forgotten all about his earlier

efforts. ‘The problem which was explicitly posed in 1961 was solved, in principle, in 1964.

No one, least of all me, knew it.’

He returned to the problems of the SU(2) × U(1) theory in 1970, in the company of

two Harvard postdoctoral students, Greek physicist John Iliopoulos and Italian Luciano

Maiani. Glashow had ﬁ rst met Iliopoulos at CERN and had been impressed with his

efforts to ﬁ nd ways to renormalize a ﬁ eld theory of the weak force. Maiani arrived at

Harvard with some curious ideas about the strength of weak-force interactions. All three

realized that their interests converged. At this stage none was aware of Weinberg’s use of

spontaneous symmetry-breaking and the Higgs mechanism.

The three physicists now wrestled with the theory once again. But they kept running up

against the same problems. Admitting the ﬁ eld particle masses by hand produced unruly

divergences. Then there was the problem of the weak neutral currents. The theory pre-

dicted that a neutral kaon should in principle decay by emission of a Z

boson, changing

the strangeness of the particle in the process and producing two muons. However, this was

a decay mode for which there was absolutely no experimental evidence. For some reason,

this particular reaction was being suppressed. But how?

Glashow was ﬁ nally ready to put two-and-two together. In doing so he would help to

sow the seeds of a major revolution in particle physics.

Even among strange particles, the neutral kaon, K

, and its antiparticle,

−

, can be regarded as ‘odd’. According to the quark model, the positive

kaon is a composite of an up quark and an anti-strange quark (us

−

), with

charges of +²⁄

and +¹⁄

adding to a total of +1. Its anti-particle is the nega-

tive kaon, a composite of a strange quark and an anti-up quark (su

−

), with

charges of −¹⁄

and −²⁄

adding to a total of −1.

For the neutral kaon, however, we have two possibilities. Both the

combinations down/anti-strange (ds

−

) and strange/anti-down (s

−

d) yield

zero net charge and, with no means to distinguish them, these two par-

ticles can form a quantum ‘superposition’, their wavefunctions overlap-

ping and combining. The result is two new neutral kaon states. The ﬁ rst

is formed from the sum of the wavefunctions of K

and K

and is referred

to as K

. The second is formed from the difference of the wavefunctions

and is referred to as K

The particles suffer something of an identity crisis. Although the kaons

are formed in their initial K

and K

states by strong-force interactions,

of charm and weak neutral currents

249

by the time the weak force acts on them they have transformed into K

and K

However, this is not quite the end of the story. When parity was shown

to be violated in weak-force interactions, it was assumed that a combi-

nation of charge conjugation (the symmetry between a particle and its

anti-particle) and parity would nevertheless be preserved.

Thus, the

superposition K

, which is even under the charge conjugation-parity (CP)

symmetry operation, can decay only into particles which are also even

under this symmetry. K

was found to decay into two pions, consistent

with this view. Likewise K

, which has odd CP symmetry, was found to

decay into three pions.

However, experiments performed at Brookhaven National Labora-

tory by Princeton physicists James Cronin and Val Fitch showed that K

kaons formed in a beam would very occasionally decay into two pions.

These events were few in number, about 50 in a total of 23,000 observed

decays, but they were much higher than expected from any background

particles left in the beam. Cronin and Fitch concluded that CP sym-

metry, too, is violated by weak-force interactions.

The explanation for this is that the states K

and K

‘contaminate’ each

other slightly. What are actually seen in experiments are not pure K

and K

, but K

, which is mostly K

contaminated with a little bit of K

and K

, which is mostly K

with a little bit of K

. The subscripts L and S

stand for ‘long’ and ‘short’, identifying these kaon states as long-lived and

short-lived neutral kaons, respectively.

The problem confronting Glashow, Iliopoulos, and Maiani in February

1970 was principally concerned with taming the divergences in their SU(2)

× U(1) ﬁ eld theory. They tried all kinds of different approaches. Iliopou-

los later described their plight. ‘Every day,’ he said, ‘invariably, one of us

would come up with an idea. Then the other two would prove to him he

was wrong. We tried all sorts of different recipes, and nothing worked.’

For example, the application of the CP symmetry operation to a spin-up electron trans-

forms it into a spin-down positron.

The reason for CP violation is still the subject of active research. Cronin and Fitch were

awarded the Nobel Prize for physics in 1980.