Baggott J. The Quantum Story: A History in 40 Moments

Подождите немного. Документ загружается.

the quantum story

190

On 2 September, he boarded another bus bound for the East coast.

‘On the third day of the journey a remarkable thing happened,’ he wrote

to his parents a few weeks later, ‘going into a sort of semi-stupor as

one does after 48 hours of bus-riding. I began to think very hard about

physics, and particularly about the rival radiation theories of Schwinger

and Feynman. Gradually my thoughts grew more coherent, and before

I knew where I was, I had solved the problem that had been in the back

of my mind all this year, which was to prove the equivalence of the two

theories.’

In work that he characterized as neither particularly difﬁ cult nor par-

ticularly clever, Dyson worked out a way of unifying the theories, com-

bining aspects of each that he judged most advantageous. The unifying

feature of his theory was something called the scattering matrix, or

S-matrix, initially proposed by Wheeler in 1937 and developed by Heisen-

berg in 1943. The S-matrix describes the process in which free particles

approach, interact, and produce particles which then separate. Each

element in the S-matrix corresponds to a Feynman diagram.

When Dyson presented his ideas to Oppenheimer back in Princeton,

he was disappointed with the reception he got, and became irritated by

what he perceived to be a defeatist attitude to QED on Oppenheimer’s

part.

Conﬁ dent of the importance of his approach to uniﬁ cation, Dyson

chose to make a stand. Oppenheimer agreed to have Dyson give a series

of seminars on the subject. The morning after the ﬁ nal seminar Dyson

found a note of surrender from Oppenheimer in his mailbox. It said,

simply, ‘Nolo contendere. R.O.’

Dyson’s ultimate triumph came at the American Physical Society

meeting in New York in January 1949. Oppenheimer was scheduled to

deliver a presidential address, his fame ﬁ lling the main hall with an audi-

ence of two thousand half an hour before the start. In his address he had

nothing but praise for Dyson’s work, claiming that it pointed the way

Oppenheimer may have had a lot on his mind. He was still quite heavily involved in Cold

War nuclear politics during what was to prove a testing period in American–Soviet relations.

The Soviet Union had begun the Berlin blockade in June 1948. This was an attempt to force the

Allies out of West Berlin by threatening to starve its population of two and a half million. War

seemed almost inevitable.

pictorial semi-vision thing

191

for the immediate future. Sitting beside Dyson in the audience, Feynman

loudly proclaimed: ‘Well Doc, you’re in.’

This statement was not strictly correct. Dyson had not yet completed

his doctorate.

There was an element of madness about it. But the result was a theory

of QED that predicts the results of experiments to astonishing levels of

accuracy and precision. The g-factor for the electron is predicted by QED

to have the value 2.002 319 304 76, with an uncertainty of plus or minus

0.000 000 000 52. The comparable experimental value is 2.002 319 304 82,

with an experimental uncertainty of plus or minus 0.000000 000 40.

‘To give you a feeling for the accuracy of these numbers,’ Feynman wrote,

‘it comes out something like this: If you were to measure the distance

from Los Angeles and New York to this accuracy, it would be exact to the

thickness of a human hair.’

The explanation? The photons created and destroyed in the virtual

processes described by the Feynman diagrams carry away some of

the mass of the electron but leave its charge unchanged, affecting the

electron’s magnetic moment.

And what of the Lamb shift? A very crude way of visualizing what

happens to an electron in an atom in QED is to think of all the virtual

processes resulting in a slight ‘wobble’ in the electron motion in addi-

tion to its orbital and spin motions around the nucleus. This wobble

‘smears’ the electron probability over a small region of space and is most

noticeable when the electron occupies an orbital that keeps it close to the

nucleus. The difference in the geometries of the two otherwise degener-

ate orbitals of the hydrogen atom is enough to account for the small dif-

ference in their energies.

These numbers are subject to constant reﬁ nement, both experimental and theoretical. The

values quoted here are taken from G.D. Coughlan and J.E. Dodd, The Ideas of Particle Physics: An

Introduction for Scientists. Cambridge University Press, 1991, p. 34. The value 2.002319304 3622(15),

where the numbers in brackets represent the uncertainty in the last two digits, is a 2006 ﬁ gure

recommended by the CODATA Task Group—see http://physics.nist.gov. The value 2.002319

304361 46(5 6) was reported in 2008 by D. Hanneke, S. Fogwell and G. Gabrielse, Physical Review

Letters, 100, 2008, 120801.

the quantum story

192

Within a few years Schwinger’s algebra had given way to Feynman’s dia-

grams as the preferred approach to QED. Schwinger didn’t like Feynman’s

approach because it was much less formal and, he believed, lacked rigour.

Having stayed for a time at Schwinger’s home in Cambridge, Massachu-

setts, theorist Murray Gell-Mann liked to report subsequently that he had

searched everywhere for Feynman diagrams, but could ﬁ nd none.

However, one room had been locked.

193

During a visit to the University of Wisconsin in 1929, Dirac was interviewed by a jour-

nalist from the local state newspaper, the Wisconsin State Journal. The journalist

appeared to take Dirac’s non-committal, monosyllabic style in his stride. Reporting on

the conversation for the beneﬁ t of his readers, he wrote: ‘. . . “And now I want to ask you

something more: They tell me that you and Einstein are the only two real sure-enough

high-brows and the only ones who can really understand each other. I won’t ask you if this

is straight stuff for I know you are too modest to admit it. But I want to know this—Do

you ever run across a fellow that even you can’t understand?”

“Yes,” says he.

“This will make great reading for the boys down [at] the ofﬁ ce,” says I. “Do you mind

releasing to me who he is?”

“Weyl,” says he.’

Hermann Weyl was a German mathematician with a particular interest in symmetry

and the representation of symmetry transformations as abstract ‘groups’.

He was also

A Beautiful Idea

Princeton, February 1954

A symmetry transformation involves the application of one or more of a variety of opera-

tions to an ‘object’, a physical system or a set of equations, with the aim to discover some prop-

erty of the object which does not change (i.e. it is invariant). Such operations include doing

nothing (called the identity operation), translations in space or time, rotations, mirror reﬂ ec-

tions, inversions, etc. Symmetry transformations can be interrelated and represented as groups,

with a transformation forming each element of the group. The group describes the results of

multiplying the different transformations together.

the quantum story

194

very well aware of the relationship between symmetry and physics. In 1915 his Göt-

tingen colleague Amalie Emmy Noether had established a principle underlying all of

physics. For any conserved physical quantity, such as energy or momentum, the physical

laws describing the behaviour of this quantity are invariant to one or more continuous

symmetry transformations. Conservation laws reﬂ ect the deep symmetries of nature.

The laws governing energy are found to be invariant to ‘translations’ in time, meaning

that the laws are the same yesterday, today, and tomorrow. Energy is therefore conserved.

For momentum, the laws are found to be invariant to translations in space—they are

the same here, there, and everywhere. For angular momentum, the laws are invariant to

rotational symmetry transformations: they are the same irrespective of direction.

Weyl applied group theory to quantum mechanics in a book published in 1928. It had

a mixed reception. Mathematicians welcomed its rigour and beauty. However, physicists

perceived it as yet another, higher level of mathematical abstraction in a quantum theory

that was already hard to understand. Pauli labelled it ‘die gruppenpest’ (the group pesti-

lence, or that pesty group business).

Hungarian physicist Eugene Wigner tried to make the subject more accessible in a

short book on quantum mechanics and atomic spectra published in 1931. Schrödinger

was dismissive of Wigner’s efforts: ‘This may be the ﬁ rst method to derive the root of

spectroscopy,’ he told Wigner, ‘But surely no one will be doing it this way in ﬁ ve years.’

Von Neumann was more reassuring: ‘Oh, these are old fogeys. In ﬁ ve years, every student

will learn group theory as a matter of course,’ he said.

Despite the fact that physicists were uncomfortable with its abstraction, it would be

symmetry considerations and group theory that would lead Chinese physicist Chen Ning Yang

and American physicist Robert Mills to the next breakthrough in quantum ﬁ eld theory.

Though it wouldn’t be recognized as a breakthrough for some time to come.

Noether’s theorem led to speculation concerning the symmetry that

could be identiﬁ ed with the conservation of another important physical

property—electric charge. It had been known since the late eighteenth

century that charge is conserved; it can be neither created nor destroyed

in physical or chemical reactions.

Weyl had worked on the representation theory of types of symmetry

groups called Lie groups, named for the eighteenth century Norwegian

mathematician Sophus Lie. These are groups of continuous symmetry

transformations, involving gradual change of one or more parameters

rather than an instantaneous ﬂ ipping from one form to another, as in a

a beautiful idea

195

mirror reﬂ ection. It is continuous symmetry transformations that under-

pin Noether’s theorem.

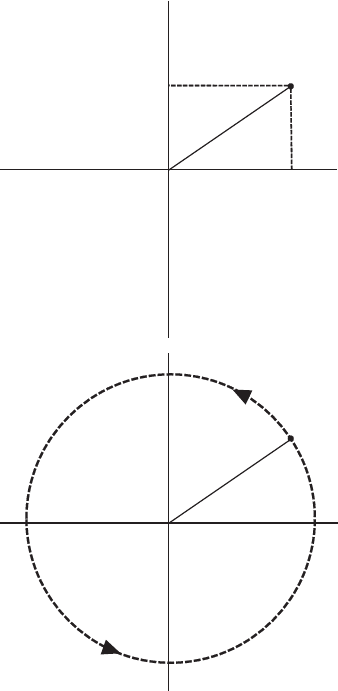
An example of a Lie group is the symmetry group U(1), the unitary

group of transformations of one complex variable. It is fairly straight-

forward to picture the symmetry transformations of U(1) in the so-called

complex plane, the two-dimensional plane formed by one real axis and

one imaginary axis. The imaginary axis is constructed from real num-

bers multiplied by i, the square-root of minus one. We can pinpoint any

complex number z in this plane using the formula, z = re

, where r is the

length of the line joining the origin with the point z in the plane and q is

the angle between this line and the real axis. This expression for z can be

rewritten using Euler’s formula as z = r(cosq + isinq ).

When the angle q is zero, the point z lies on the real axis a distance +r

from the origin. After applying a rotation through 90°, the point z now

lies on the imaginary axis a distance +r from the origin. A further 90°

rotation brings z back to the real axis, but this time lying −r from the

origin. Another 90° rotation brings z to the imaginary axis once again,

now pointing a distance −r from the origin. A ﬁ nal 90° rotation takes us

back to where we started. It quickly becomes apparent that a continu-

ous transformation through the angle q moves the complex number z

through a circle in the complex plane.

What Weyl discovered was that this symmetry property is somehow

related to the conservation of charge. In Maxwell’s equations of classical

electromagnetism, it is the intimate relationship between the electric and

magnetic ﬁ elds which preserves this symmetry and ensures that charge

is conserved. A static charge generates a static electric ﬁ eld, but a moving

charge generates both an electric and a magnetic ﬁ eld.

But Weyl went further. Symmetries can be global or local. In a global

symmetry the object is invariant to changes that are applied uniformly,

at all points in space–time.

In a local symmetry the object is invariant to

An example of a global symmetry change is a uniform shift in the lines of latitude and lon-

gitude used by cartographers to map the surface of the earth. So long as the change is uniform

and applied consistently across the globe, this makes no difference to our ability to navigate

from one place to another.

the quantum story

196

Real axis

Imaginary axis

–

(a)

(b)

r cosθ

ir sinθ

fig 11 The symmetry group U(1) is the unitary group of transformations of one

complex variable. In a complex plane formed by one real axis and one imaginary

axis, we can pinpoint any complex number z using the formula z = re

, where r is

the length of the line joining the origin with the point z in the plane and h is the

angle between this line and the real axis, (a). A continuous transformation through

the angle h moves the complex number z through a circle in the complex plane, ( b).

There is a deep connection between this continuous symmetry and simple wave

motion, in which the angle h is a phase angle, as illustrated in (c) see next page.

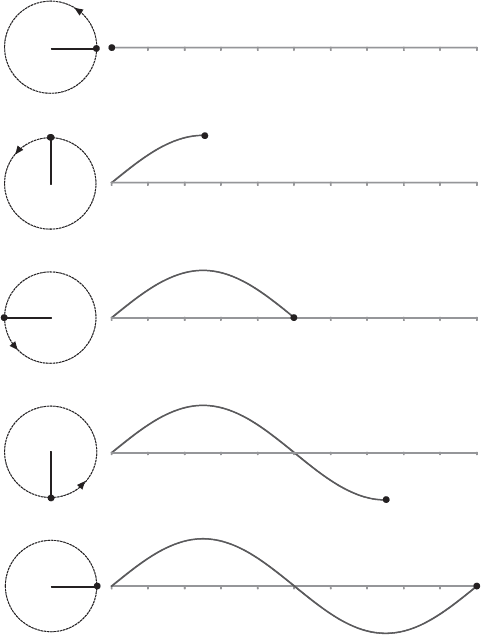
a beautiful idea

197

θ =0

θ = 90°

θ = 180°

θ = 270°

θ = 360°

(c)

changes applied non-uniformly, with different changes at different points

in space–time. It was later shown that the conservation of charge is related

to invariance to local symmetry transformations. Requiring the symmetry

to be local demands that the electric and magnetic ﬁ elds be connected pre-

cisely in the way described by Maxwell’s equations. Another way of look-

ing at this is that local invariance demands a ﬁ eld that ‘kicks back’ when

changes are made, restoring local symmetry and so conserving charge.

Weyl was working on these ideas before the advent of quantum

mechanics, and chose to give this symmetry the generic name gauge sym-

metry. He was thinking of symmetry in relation to the distances between

the quantum story

198

points in space–time, and was guided by Einstein’s work on general

relativity. Weyl initially ascribed the invariance to space itself, leading

Einstein to point out that if this were true, a clock moved around a room

would no longer keep time correctly.

In 1922 Schrödinger had identiﬁ ed Weyl’s ‘gauge factor’ as a phase fac-

tor, pointing out that transformations of the phase through integral mul-

tiples of 360° leaves the phase unchanged. At the time it was not at all

clear what this meant, other than providing a clue to the origin of the

quantum numbers, the ‘integral multiples’. When Schrödinger discov-

ered wave mechanics three years later, it became clear that the phase is

associated with the electron wavefunction.

Another way of representing U(1) is in terms of continuous transfor-

mations of the phase angle of a sinusoidal wave. A transformation of 180°

will put the wave ‘out of phase’ with the original wave. A further 180°

transformation will bring the wave back in phase. This is entirely analo-

gous to the movement of the complex number z in the complex plane

considered above.

But the mechanism by which symmetry is preserved is subtly dif-

ferent in quantum mechanics. The change in phase we are now con-

sidering affects the wavefunction of the electron as a material particle.

Symmetry is preserved if changes in the phase of the material wavefunc-

tion are matched by changes in its accompanying electromagnetic ﬁ eld.

Gauge invariance generates a force, and the force ﬁ eld must ‘kick back’.

The particle and the ﬁ eld are now intimately connected. What Weyl

had actually discovered was the connection between the local phase

symmetry of the wavefunction and the conservation of charge.

The gauge symmetry of U(1) phase transformations is a characteris-

tic of all quantum theories of the electron, including QED. As physi-

cists began to think about the formulation of quantum ﬁ eld theories to

describe the strong force between protons and neutrons in the atomic

nucleus, the question inevitably arose: What could be the relevant gauge

symmetry for such a ﬁ eld?

The challenge was ﬁ rst to ﬁ nd a property that is conserved. Chinese phys-

icist Chen Ning Yang had arrived at the University of Chicago in 1946 to

study nuclear reactions under the supervision of Edward Teller. He had

a beautiful idea

199

adopted a middle name ‘Franklin’ or just ‘Frank’, after reading the auto-

biography of the American inventor and politician Benjamin Franklin.

He obtained his doctorate in 1948 and worked for a further year as an

assistant to Enrico Fermi. In 1949 he moved to the Institute for Advanced

Study in Princeton.

Yang was struck by the notion that in electrodynamics charge conserva-

tion is predicated on the gauge invariance of the phase of the electron wave-

function. It was in Princeton that he began to think about ways in which

he could apply the principles of gauge invariance to the strong force that

binds protons and neutrons in atomic nuclei. As far as he was concerned,

the quantity that is preserved in strong nuclear interactions is isospin.

The concept of isospin, or isotopic spin, grew out of the observation

that the masses of the proton and neutron are very similar. At the time

the neutron was discovered in 1932, it was perhaps natural to imagine

that the neutron was a composite particle consisting of a proton with

an electron stuck on to it. After all, it was also known that beta radioac-

tive decay involves the ejection of high-speed electrons directly from the

nucleus, turning a neutron into a proton in the process. This seemed to

suggest that in beta-decay, the composite neutron was somehow shed-

ding its ‘stuck-on’ electron.

Heisenberg preferred to think of the neutron as a fundamental particle,

but nevertheless picked up on the neutron-as-proton-plus-electron idea

to develop an early theory of proton–neutron interactions in the nucleus.

This was a model analogous to the chemical binding of two protons by

a single electron in the ionized molecule H

He hypothesized that, just

as the two protons in H

are bound together by a single electron, so the

proton and neutron bind together in the nucleus by exchanging an elec-

tron between them, the proton turning into a neutron and the neutron

turning into a proton in the process. By the same token, the interaction

between two neutrons would involve the exchange of two electrons,

one in each ‘direction’, analogous to the chemical bond in molecular

hydrogen, H

The neutral hydrogen atom H consists of one proton and one electron. The ionized

hydrogen molecule H

therefore consists of two protons bound together by a single electron.