Backman Clifford R. The Worlds of Medieval Europe
Подождите немного. Документ загружается.


244 THE CENTRAL MIDDLE AGES
common practice of Jewish scholars—the astronomer Abraham ben Hiyya is a
good example—of not translating books out of Arabic but of transliterating them
into Hebrew letters. Most Jews of the southern half of the Mediterranean basin,
from Spain to Syria, spoke Arabic and/or another local vernacular rather than
Hebrew. Hebrew was the language of liturgy and scholarship—as Latin was for
Christians—but it was not necessarily the everyday tongue of the common laborer
or shopkeeper; nevertheless, most Jews would have received enough education in
their synagogue to read Hebrew letters.
9
Jewish physicians were highly prized at
Islamic and Christian courts, even though Christian law technically forbade them
to practice on Christian patients (Islamic law had no such strictures), and many
Muslim and Christian students flocked to study with Jewish physicians. Interest-
ingly, Jewish physicians in the Middle Ages made very few contributions to med-
ical knowledge—that is, they did little “original research”—but in terms of treating
illness they were peerless until the mid-thirteenth century when the establishment
of the medical school at the University of Montpellier in southern France put Latin
Christendom for the first time on roughly the same level of scientific sophistication.
The first signs of a Latin scientific revival appeared in the field of medicine
in the late eleventh century in Italy, specifically at the southern city of Salerno.
This city had long had close links with Islamic Sicily, and scholars there learned
a good deal of Muslim medicine (which the Muslims themselves, of course, had
largely derived from the Greeks). Salerno, in fact, quickly emerged as the first
center for advanced medical study in Latin Europe, just as Bologna emerged as
the center for legal studies. The best known of the Salernitan medical scholars
were Constantine the African, a monk-translator at Monte Cassino in the second
half of the eleventh century, and a woman named Trotula, who lived sometime in
the twelfth century. Trotula wrote an influential work called The Diseases of Women,
the first gynecological treatise in Western history; throughout the Middle Ages
women commonly served as midwives and providers of basic health care to other
women, but Trotula was the first, and for a long time virtually the only, woman-
practitioner actually to put her knowledge into writing. Like Constantine, she sub-
scribed to the traditional model derived from the second-century Greek physician
Galen, who posited that the human body is composed of four fluids called humors
that govern our health and disposition. Galen identified these humors as blood,
phlegm, choler (yellow bile), and melancholy (black bile). It is a combinatorial
theory of medicine: The interactions of these humors, and the fluctuations of their
temperatures and degrees of moisture, react with the workings of the various
organs to produce health or illness. Trotula, like all medieval physicians, followed
the Galenic model but added to it empirical knowledge that she had gathered
from her practice. It is possible, too, that she learned more about anatomy through
dissection—which we know was performed at the medical school in Salerno in
the twelfth century. Trotula’s book moves back and forth between theory and
practice, with light touches of autobiography added for good measure.
God distinguished the human race beyond all other creatures by granting it
an extraordinary virtue...thefreedom to reason and think....Since women
are by nature weaker than men it stands to reason that illnesses plague them
more frequently; this is especially true regarding the procreative organs. But
9. As the huge trove records in the Cairo geniza shows, medieval Jews commonly wrote everyday
documents like business contracts, shopping lists, personal letters, wills, diaries, memoranda, and re-
ceipts in Hebraicized Arabic. These records have been exhaustively studied by Shlomo Goitein in his
five-volume work called A Mediterranean Society.

THE RENAISSANCES OF THE TWELFTH CENTURY 245
since these organs happen to be in, as it were, a recessed location, women’s
modesty, not to mention the delicacy and sensitivity of these organs, com-
monly prevents them from bringing their troubles to male doctors. For that
reason I, out of sympathy for their situation and at the urging of a certain
prominent lady, began to study in earnest the maladies and complaints that
women are vulnerable to.
Trotula writes of diet, hygiene, skin care, menstruation, and pregnancy. Also how
to avoid the latter—and it is in some of her precise recommendations that we
perceive the survival of folk medicine within the broader Galenic theory.
Galen notes that “women with narrow vulvas and small wombs ought not to
marry, for they risk death if they become pregnant.” But since not all women
can avoid [marriage and pregnancy], they need help. If a woman fears death
and so seeks not to conceive, she should wear next to her naked flesh the
womb of a virgin she-goat....Shemight also try removing the testicles from
a weasel—without killing it—and wear them upon her bosom wrapped in
the skin of a goose or some other animal skin. Then she will not conceive.
Despite such passages, The Diseases of Women is filled with much valuable infor-
mation, especially on the use of medical herbs and ointments, and it became the
standard text on women’s health at Salerno. By the thirteenth century, however, a
new medical school opened up at Montpellier in southern France, and as it rose
to prominence Salerno and Trotula declined in influence.
More solid achievements were made in mathematics, geometry, and astron-
omy. Translators from England were especially important here. In the 1120s Ade-
lard of Bath, who learned Arabic in Sicily, translated an Arabized version of Eu-
clid’s work on geometry and ’al-Khwarizmi’s treatise on trigonometry.
’Al-Khwarizmi (800–847) is usually credited with having introduced “Arabic nu-
merals”—which actually originated in India—to the west. That might seem at first
like a relatively modest development; but European mathematics had long been
hampered by the use of Roman numerals, whose inherent limitations become ob-
vious if one tries to multiply mccxlviii by dcciv instead of 1248 by 704. Al-
Khwarizmi also wrote a book called The Restoration and Opposition of Numbers that
was translated by another Englishman, Robert of Chester, around 1150. So signif-
icant was this work that later Arab mathematicians referred to it simply as “The
Book,” which in Arabic is al-jibra—now the bane of many a Western adolescent.
The greatest Latin mathematician of the Middle Ages was Leonardo Fibonacci
(1170–1230), sometimes known as Leonardo Pisanus or Leonardo of Pisa. He made
his mark in 1202 when he published his Book on the Abacus, in which he explored
the possibilities of decimal-based mathematics. He developed a sequence of num-
bers known as the Fibonacci sequence that was to have important implications. It
goes like this:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...
In the sequence, each number is the sum of the two numbers that precede it.
Fibonacci developed the algebraic formula to express this sequence; it is called a
recursion relation. The significance of the formula, for our purposes at least, is that
it describes a surprising number of natural phenomena. The formula, when
mapped on a graph, corresponds exactly with the spiral arrangement of petals on
flowers, the curve of snail shells, the twisting array of branches around the trunk
of a tree. The ratio of pine leaves on opposed spirals of a pine cone is always 5:
8; of bumps on a mature pineapple 8:13; of seeds in the center of a sunflower 21:

246 THE CENTRAL MIDDLE AGES
34—all of which are adjacent Fibonacci pairs. The number of rabbits produced in
a litter under ideal conditions is always a Fibonacci number. Moreover, once one
progresses several places into the sequence, the ratio between the adjacent num-
bers of the sequence becomes constant and approaches a quantity that the ancient
Greeks called the Golden Mean: 1.618.
10
Many other correspondences exist—and
so Fibonacci’s discovery did much to affirm the medieval certainty that they lived
in a rationally ordered world. His formula was later used by Renaissance artists
and architects to design the curves and ratios they used to create what they re-
garded as perfect balance and proportion.
In astronomy the most important developments were the translation of Ptol-
emy’s Almagest, the most comprehensive work of the Greeks, at Palermo in 1160,
and again at Toledo in 1175. Medieval astronomers preferred the Toledan version
since it came equipped with the Arabic commentary. But meanwhile the wide-
spread use of the astrolabe, a device for measuring the position of stars and planets
in the night sky, made possible much more precise mapping of planetary positions.
The astrolabe had been known as early as the late tenth century: in fact, Gerbert
of Aurillac, Pope Sylvester II, was one of the first figures in the west to study it.
But the astrolabe was not widely applied until the twelfth century when it helped
to advance astronomical knowledge and made navigation easier and more reliable.
Several technological developments emerged around this time as well. One of
the most important was a new type of mill. Latin Europe had been limited to
water mills for centuries; hydraulic power was plentiful but problematic. Mills
obviously could only be located along major waterways, which placed a clear limit
on human settlement; mills also strengthened the hierarchical structure of feudal-
manorial society, since one often had only to control a strategic waterway, mill, or
bridge in order to maintain effective power over an entire community. This is one
reason why we see lords and vassals, in feudal contracts, speaking quite precisely
about water rights. But in the twelfth century, the first windmills began to appear
in Europe. Knowledge of their design probably was brought back to Europe by
the soldiers of the First and Second Crusade, for we know that the people of
Palestine, Syria, and Iraq had developed windmills at least by the late tenth cen-
tury. Windmills could be constructed anywhere and were less vulnerable to sea-
sonal change than water mills. They allowed free farmers to remain free by giving
them the chance to mill their grain without having to go to a manorially controlled
mill; in their small own way, windmills were often emblems of resistance to feudal
control of the countryside.
Other new technologies that appeared included the start of a silk-weaving
industry, the first efforts to build mechanical clocks, the first experiments at optics
and the preparation of lenses, the distillation of spirits (brandy out of wine, chiefly,
but there are signs of something like a rough whiskey being made in Ireland and
Scotland), the introduction of the magnetic compass for navigation, the develop-
ment of the galley as the main seagoing ship, the construction of stone castles and
churches (which we will discuss in Chapter 14), the appearance of vernacular
poetry and polyphonic music.
10. This is getting a bit esoteric. To the Greeks the Golden Mean was an ideal ratio to create visual
beauty. Imagine a line segment AB. At some point along that line there is a point X. The ideal proportion
is reached when AX is to XB as XB is to AB, which is a ratio of 1.618. This Golden Mean was used
throughout Greek architecture (it governs the proportions of the Parthenon, for example) and sculpture
(the Venus de Milo).

THE RENAISSANCES OF THE TWELFTH CENTURY 247
T
HE
R
ISE OF THE
U
NIVERSITIES
It seems a natural consequence that all this intellectual activity would sooner or
later find some sort of institutional organization; ideas exist, after all, in order to
be shared with others—or else they are no good as ideas. But how to organize the
new learning of this time? The twelfth century was a time of great intellectual
vibrancy and curiosity, but perhaps as a consequence it was also a time of consid-
erable intellectual disorder. The only hope for coming to some sort of meaningful
agreement about all these new discoveries was if the scholars themselves learned
from one another. This seemed a reasonable hope, since the medieval mind was
so powerfully geared toward the idea that all knowledge interrelated with all other
knowledge.
The origins of the new schools that came to dominate European intellectual
life are somewhat obscure. Certain models date back to classical times: Both Plato
and Aristotle had founded academies in Athens where they regularly gave lec-
tures, and in Roman times there had been organized centers of study at places
like Alexandria and Antioch. In Islam, the institutions of the majlis and madrasas
(Qur’anic bookstores and schools, usually attached to a mosque) also provided
certain precedents, while Jewish synagogue schools provided another model. And
of course, Christendom had its enormous network of monastic schools. By the
twelfth century these were largely disdained, however. The monastic vocation was
still deemed a noble one—but that was part of the problem; monastic life had
become monopolized, it seemed, by the aristocracy, and monasteries, no matter
how reformed and holy, were commonly regarded as sanctified country clubs.
Moreover, monastic education was too limited in scope; it aimed only to help the
student become a better monk. Therefore a new type of school was needed, one
where all the new learning in philosophy, science, art, mathematics, music, and
“humane letters” (litterae humaniores) could be studied.
11
At first these new ideas circulated through Europe via itinerant scholars like
Peter Abelard, but eventually it became clear that a more permanent educational
system needed to be devised. Once again the bishops took the lead. By attaching
schools to their cathedrals they achieved a variety of goals: They placed themselves
in a position to attract and observe the most talented young people for entry into
the priesthood; they assured themselves of an important additional source of rev-
enue; they raised their social profile by being the providers of social advancement;
and they exerted a degree of control over the new learning as it emerged under
their watchful eyes. The medieval cathedral schools—and the universities they
would evolve into in the thirteenth century—differed from all their forerunners in
several critical ways. They offered standardized curricula; those curricula were
taught by organized, incorporated bodies of professors; and, in their most radical
innovation, they bestowed formal degrees upon those students who completed the
curricula. Henceforth, education was an empirical, legal fact, not merely a state of
mind.
And so the schools began to grow. The school at Angers, in the Loire valley,
produced scholars like the trouble-making Berengar of Tours and the reformers
Robert of Arbrissel and Marbode of Rennes. Constantine the African and Trotula
made Salerno the best place to study medicine. Irnerius single-handedly estab-
11. The “humane letters” were not part of the universities’ curriculum until the late thirteenth century.

248 THE CENTRAL MIDDLE AGES
lished Bologna’s reputation as the premiere site for legal study. But these are just
the “marquee” names; thousands of scholars in hundreds of towns filled lecture
halls across Europe, teaching tens of thousands of students. Even in a small town
like Bergamo, in northern Italy, the cathedral school had nearly two dozen full-
time faculty by the middle of the century, a company capable of handling ap-
proximately six hundred full-time students. Schools in larger cities were even
larger, both in absolute numbers and in the ratio of students to teachers. To the
extent possible, the schools always retained their professional mission—the prep-
aration of clergy—but they were quick to open their doors to other ideas and goals
as well. One frequent problem was that most of these schools were led by a single
master (Latin magister), normally appointed by the bishop, with the majority of
tutorials and lectures conducted by the cathedral canons, whereas most of the new
advances in legal, philosophical, and scientific scholarship were being made by
the itinerant scholars who, while they never really sang for their supper, were
usually willing to lecture for it. Consequently, schools began to offer more or less
permanent positions to these scholars in return for their services as popular teach-
ers. William of Champeaux was one of these early scholars-in-residence. Others
included, obviously, Peter Abelard, who took William’s job from him, and scholars
like Hugh of St.-Victor. Schools had to compete for these celebrity faculty, much
as today’s universities do.
A school that had the foresight and means to attract more than one scholar—a
philosopher and a legal theorist, for example, with perhaps a couple of grammar-
ians, mathematicians, astronomers, and physicians thrown into the mix—soon con-
fronted a problem: how to manage the inevitable rivalries between them? Aca-
demicians have been prima donnas from the start, and dealing with their scholarly
egos has been a problem for school administrators for just as long. More impor-
tantly, how did a school establish uniform standards of service and expectations?
The answer lay in creating a formal university. The word university derives from
the Latin term universitas, which was the word for a “commercial guild.” That is,
a universitas was a legal corporation that established its own standards, regulated
itself, and enjoyed certain legal privileges. The universitas established its own
criteria for what it expected of its students, and it rewarded those students who
satisfied those criteria by bestowing on them a formal recognition of their achieve-
ment—just as a mercantile guild recognized a journeyman who learned all the
skills of a certain trade by elevating him to the status of master and admitting
him into the guild. Thus originated university curricula and degrees.
As self-governing institutions, universities stood outside the jurisdiction of the
cities that gave them a home, just as cities themselves existed outside the juris-
diction of the feudal districts in which they were located. This “town-gown” dis-
tinction led to frequent conflict, since every university attracted students from
across Europe, and consequently each university was often a microcosm of what-
ever political tensions and conflicts engulfed Europe. Arguments and general row-
diness were common and local city officials were relatively helpless to do anything
about it, since university students were keenly aware of their legal privileges. In
frustration, people sometimes resorted to vigilante justice, which possibly explains
the origin of the three most famous universities in Europe. In 1200 a group of
German students at the University of Paris rioted in the city streets—possibly over
an ongoing dispute between England’s King John and Germany’s Otto of Bruns-
wick, who was trying to court John’s support in his campaign to win the German
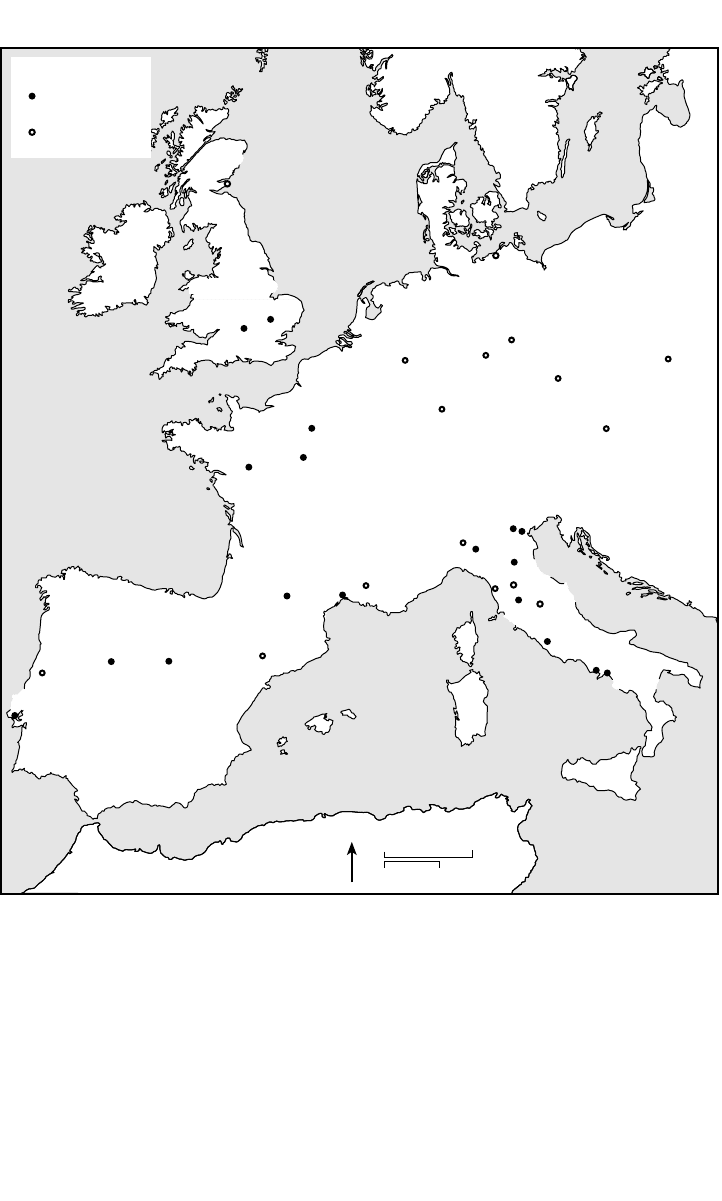
THE RENAISSANCES OF THE TWELFTH CENTURY 249
0 200 Miles
0 200 Kms.
N
ATLANTIC OCEAN
North Sea
Baltic Sea
Adriatic Sea
MEDITERRANEAN SEA
Tyrrhenian
Sea
Vicenza
(1204)
Bologna
(1158?)
Piacenza
(1248)
Pavia
(1361)
Salerno
(9th Cent.?)
Rome (1244)
Naples (1224)
Perugia
(1308)
Padua
(1222)
Florence (1349)
Siena
(1247)
Pisa
(1343)
Montpellier
(1289)
Toulouse
(1229)
Lérida
(1300)
Valladolid
(1230)
Avignon
(1303)
Sorbonne
(1253)
Angers
(1229)
Orleans
(1250)
Salamanca
(1218)
Lisbon
(1290)
Coimbra
(1308)
Cambridge
(1209)
Paris
(c. 1150)
St. Andrews
(1413)
Cologne
(1388)
Erfurt
(1379)
Leipzig
(1409)
Prague
(1347)
Cracow
(1397)
Vienna
(1365)
Rostock
(1419)
Heidelberg
(1385)
Oxford
(1167)
SPAIN
PORTUGAL
FRANCE
ITALY
GERMANY
POLAND
HUNGARY
SCANDINAVIA
IRELAND
ENGLAND
SCOTLAND
E. McC. 2002
Medieval Universities
Established
before 1300
Established
after 1300
Medieval universities
imperial crown—and a Parisian mob, led by the local police commissioner, coun-
terattacked, leaving one student dead and many more wounded. The university’s
English students and masters, fearing that Paris was becoming too hostile, fled
back to England in search of a spot where they could establish a school of their
own. Thus began Oxford University. But only nine years later, in 1209, a group of
drunken Oxford students assaulted a local girl of the town, which led the citizens

250 THE CENTRAL MIDDLE AGES
to rise up in arms against them and drive them out. The hooligans looked about
for another refuge, a place to start yet another school for themselves. Thus began
Cambridge University. Other universities sprang up quickly; these were not
wholly new institutions in every case, but often were cathedral schools of long
standing that simply received a new legal status: Padua in 1222, Naples in 1224,
Toulouse in 1229. By the year 1300 there were nearly two dozen universities in
Latin Europe, and by the year 1500 there were seventy-nine.
Whether established by pope, emperor, king, count, or commune, universities
were overwhelmingly episcopal institutions. The bishops were their nominal
heads, although usually the officer who ran each bishop’s chancery was the fellow
who performed their day-to-day administration (and that is why university heads
today are commonly called chancellors). In an effort to provide a greater degree of
continuity and standardization between the degrees offered by each university, the
papacy was quick to take action. The Holy See bestowed the title of studium gen-
erale (“general school”) upon schools that met its standards of mastery within each
of the subjects studied. Not surprisingly, the emperor insisted on his ability to
establish a studium generale also, and until the end of the Middle Ages both
figures did so. The recognition mattered. Receiving one’s degree from a studium
generale gave one the right to teach one’s subject anywhere; degrees from lesser
institutions were less portable. With this new system of accreditation, the ration-
alization of education caught up with the rationalization of thought itself that so
distinctively characterized the twelfth-century renaissance.
Whatever the subject, lecturing by gloss was the primary method of teaching.
A gloss was a commentary upon an authoritative text: thus a professor of canon
law would teach his subject by reading a passage from Peter Lombard’s Sentences,
then commenting on it at length, pointing out grammatical nuances, fine stylistic
points, allusions to literary texts, references to earlier canonical collections or to
patristic literature, and quotations from Scripture, and then drawing attention to
parallel or contrasting passages elsewhere within Lombard’s own text. Then he
would move on to the next passage, and repeat the entire process, and so on until
he had read and glossed the entire text. A law professor would do the same with
the Corpus, a medical professor with a text of Galen or Hippocrates, a philosophy
professor with a text of Aristotle or Plato. This method served at least two fun-
damental purposes: it retained the authority of the texts themselves, assuring that
they provided the bedrock for all subsequent thought, and it offered a way for
students to procure working copies of the texts. Books were still too expensive for
most (non-noble) students to afford easily. The method of reading out a single
paragraph a day, and commenting carefully upon it word by word and line by
line, gave students a chance to write out their own copies. The method may strike
modern readers as hopelessly dull, but in the twelfth century it generated extraor-
dinary intellectual excitement: The newest and most advanced ideas in every field
were being circulated in the most democratic way possible. The new schools were
raucous, lively, exuberant places, in sharp contrast to the earnest toilsome quiet of
the monastic schools.
So raucous, in fact, that they caused a good deal of trouble. Most students
began their college careers around the age of fifteen, provided that they could
prove mastery of Latin. The trivium and quadrivium remained the basic curricular
structure, although faculty were allowed a certain amount of freedom to innovate
and to introduce new texts. After a year or two, students were encouraged to ask
questions during their professors’ lectures and to debate them publicly on certain

THE RENAISSANCES OF THE TWELFTH CENTURY 251
occasions. After four or five years a student, then aged twenty, took a set of oral
examinations which, if he passed, earned him a bachelor’s degree. This qualified
him to serve as an assistant lecturer, much like a teaching assistant in an American
graduate school today. After two or three years of assistant teaching, during which
time he would continue advanced studies in specialized topics, the student would
proceed to another set of oral examinations, after which he was required to present
a public lecture and engage in a disputation with a panel of scholars. At the
disputation the student was required to argue his points with detailed references
and, when called for, quotations from the texts he had studied. If he passed this
hurdle, he received a master of arts degree and was licensed to teach or become
a clerk. Few opted to continue on for a Ph.D. since it required so many more years
of study (by statute, law required at least six more years, medicine eight, and
theology twelve).
Two observations stand out. First, educated people in the Middle Ages had
prodigious memories. With books so rare and their contents so highly prized, it
should not surprise us—and yet it does—that medieval scholars could retain so
many volumes of text in their heads. The poet Dante Alighieri reportedly could
recite the entire text of Virgil’s Aeneid (over three hundred pages of verse, in mod-
ern editions) from memory. Well-disciplined monks had little difficulty in reciting
the entire Psalter. The itinerant scholars who contributed so much to the intellec-
tual revival of their age traveled with only the library in their memory lobes. When
Peter Abelard compiled his Sic et Non, with all its contradictory passages from the
patristic Fathers, Church councils, papal decrees, and Biblical verses, he wrote
most of them out from memory. Studying in the Middle Ages involved spending
as much time memorizing texts word for word as it did analyzing them logically,
and indeed most scholars would have insisted that the latter is not truly possible
without the former.
An important consequence of this learning-by-memorization method, though,
is that medieval scholarship remained conservative even when it was most radical.
It is true that university students read a body of materials that was exponentially
broader in scope than what monastic students were exposed to, but the fact that
those broader studies became focused and anchored upon their own set of au-
thoritative texts—Lombard’s Sentences, the Corpus, Gratian’s Decretum, Aristotle’s
Works, Euclid’s Geometry, Ptolemy’s Almagest, Galen’s Medicine, or whatever—
meant that medieval scholarship never became so daring as during this initial
twelfth-century era when the new canon was formulated. Once the curriculum
was established, however, basic innovation became less and less frequent. Intel-
lectual life in the thirteenth century was in many ways a brilliant culmination of
what the twelfth-century innovators had accomplished, but it was in some respects
less fundamentally exciting. We need to temper our sense of the radicalism of the
age with a sense of the strictures that still remained on scholars.
Second, while most tuition was not prohibitively high and while teaching
methods were designed partially to help students provide themselves with copies
of the books they would need, the time spent on university education meant that
young men who came from rural or urban working families were effectively ex-
cluded. To support a young man from age fifteen to his early twenties—during
the height of his youthful strength and energy, when those qualities were sorely
needed in the fields or shop—was more than most lower-income families could
afford. Thus even though medieval education was theoretically open to anyone
(male, that is) who could pay the tuition, in point of fact it remained a virtual

252 THE CENTRAL MIDDLE AGES
monopoly of the middle class and the lower nobility. (The upper nobility generally
disdained the universities and preferred to hire private tutors for their children.)
The schools were engines of social mobility, particularly if one received an ad-
vanced degree in law, medicine, or theology. To encourage such mobility and to
secure a sufficient pool of talent for administrative and professional needs within
the city, many towns began to offer scholarships to urban youths. Wealthy indi-
viduals endowed scholarships or hostels for housing students who were either of
a particular nationality or following a particular course of study; The Colle`ge de
Sorbonne began as a hostel created by the wealthy Parisian Robert de Sorbonne
for students wishing to study theology at the University of Paris.
12
Universities commonly housed students by their nationality regardless of their
course of study. This practice had the effect of sometimes making universities
miniature Europes—and they often reflected on the university site some of the
political tensions that existed between the European states at any given time. If
France and Germany were at war, for example, then there was a good chance that
the French colleges and German colleges were taunting one another at universities
all across Europe. This is one reason why universities from their very inception
acquired reputations as havens for young troublemakers, rowdies who needed
only the prospect of a weekend free of classes and a visit to a local tavern in order
to start hellraising. Of course, the rigors of their studies—and the pursuit of some
of the other things that are on the minds of young men in their late teens and
early twenties—no doubt added fuel to the fire. Aliqui nunquam cambiunt (“Some
things never change”).
C
OURTLY
L
IFE
,L
OVE
,
AND
L
ITERATURE
The universities were not the only places where cultural and intellectual life flour-
ished. The other principal site of these energies was the aristocratic courts. By the
twelfth century, the chivalric code had evolved into a sophisticated cultural prac-
tice that expected far more of a knight than prowess in arms. A knight was un-
derstood to be an ideal form of secular Christian—pious, magnanimous, charita-
ble, learned, polite, and cultured as well as brave. To the twelfth-century chivalric
mind, Lancelot (minus that naughty business with Queen Guinevere) was the ideal
knight, whereas the brutish Roland had been the measure of perfection to
eleventh-century knights. Twelfth-century knights were still expected to be un-
surpassed warriors, but they were now expected to be so much more besides.
Their representations in the popular literature of the age represents this shift. New
genres emerged to tell of their exploits; in an even greater innovation, court poets
began to sing the glories of their chivalric heroes in their vernacular tongues.
The chivalric code was based on courtesy, not in the sense of “politeness” but
of “courtliness.” Courtly manners, deportment, and values became the fashion of
the age, and added a civilized veneer to the warrior essence of the knightly class.
The ability to smash in a pagan’s skull with a battle-ax may have been the chief
prerequisite for entry into the best society in Clovis’ or Charlemagne’s time, but
twelfth- and thirteenth-century Europe demanded more refined achievements. Af-
12. Presumably if they all lived together they could encourage each other to avoid temptation. Robert
seems to have regarded four acts as particular temptations to watch out for, to judge from the statutes
he designed for his college: a preference to dine alone instead of in the main hall, a desire to wear loud
clothing, an interest in maintaining contact with secular persons, and a wish to possess a key to the
kitchen.

THE RENAISSANCES OF THE TWELFTH CENTURY 253
Illuminated initial from English copy of the Letters of Pope
Gregor y I. Twelfth centur y. English scribes in the Middle Ages
were particularly well known for the vitality and fluidity of their
draftsmanship. This example, from a twelfth-centur y copy of the
Letters of Gregor y I, shows a noble warrior— identifiable from his
stance on top of a common foot-soldier, plus his brandishing of a
fine sword — fighting a two-headed dragon. It is a brightly colored
image, filled with hues of airy blue, green, gold, light copper, and red.
(Giraudon/Art Resource, NY)
ter all, the pagans were gone and the Muslims were the chief trading partners of
the Christians in the south. The courtly lover was expected to be daring and pious,
to dedicate himself to the praise of his beloved, and to strive for the greater glory
of her fame and his own reputation for steadfast loyalty by performing heroic
exploits. Lyric poetry was a suitable genre for professing great love, but narrating
the exploits performed in love’s service was the purview of romance. These verse
narratives tell of secret meetings between lovers, stolen kisses, narrow escapes
