Автор не указан. Физика: формулы и определения: Шпаргалка

Подождите немного. Документ загружается.

42.ДВИЖЕНИЕИСКУССТВЕННЫХ

СПУТНИКОВ(ПРОДОЛЖЕНИЕ)

Формула

VgR= .

не учитывает расстоя-

ние спутника от поверхности Земли и зави-

симость ускорения СП тела g

от высоты H.

Если тело вращается вокруг Земли по кру-

говой орбите, то в формуле 1-й космической

скорости необходимо записать ускорение

СП в зависимости от высоты Н над поверх-

ностью Земли и радиуса орбиты r = R + H.

Получим

Vgr

ψψ

()

() .

Аналогичные формулы 1-й космической

скорости можно получить, считая, что сила

тяжести, действующая на спутник, являет-

ся центростремительной силой.

Вторая космическая скорость — та на-

именьшая скорость, которую надо сооб-

щить телу, чтобы оно могло преодолеть

притяжение Земли и превратиться в спут-

ник Солнца. Она равна:

VgR==2 11,2км/с.

43.ИМПУЛЬСЧАСТИЦЫИИМПУЛЬС

СИЛЫ

Второму закону Ньютона F



= ma



можно

придать другую форму, «расписав» уско-

рение. Получим



∆

Но m = const, тогда



∆

Обозначим P



= mV



Векторная величина, равная произведе-

нию массы частицы на вектор скорости ее

движения, — импульс частицы.

Тогда второй закон Ньютона будет зву-

чать так: скорость изменения импульса час

тицы равна действующей на эту частицу

внешней силе.

Приращение импульса частицы за проме-

жуток времени Dt будет DP



= F



Dt.

Произведение силы на время ее действия

называется импульсом силы.

44.ЗАКОНСОХРАНЕНИЯИМПУЛЬСА

Закон сохранения импульса: суммарный

импульс замкнутой системы остается по

стоянным по модулю и направлению, хотя

импульс каждого из тел системы может из

меняться. Докажем это.

Силы, действующие в системе тел, под-

разделяются на внутренние (силы взаимо-

действия тел системы между собой) и вне-

шние (силы, действующие на тела системы

со стороны тел, не входящих в нее). За-

мкнутой называется система тел, если на

нее не действуют внешние силы.

Для каждого из п тел некоторой системы

изменение ее импульса DP



за время Dt мож-

но найти по второму закону Ньютона:



= (f



+ F



)Dt, DP



= (f



+ F



)Dt, …,



= (f



+ F



)Dt,

где f



, f



, …, f



и F



, F



, …, F



— равнодей-

ствующие внутренних и внешних сил для

каждого из тел.

Сложим векторно левые и правые части

всех n равенств.

Т.к.

∑

(сумма внутренних сил равна

нулю по третьему закону Ньютона), то

∆∆



PFt

∑∑

Для замкнутой системы



∑

тогда



∑

Значит,



∑

const.

Обозначим



∑



, где P



— импульс сис-

темы тел.

Получим P



= const, что и требовалось до-

казать.

45.РЕАКТИВНОЕДВИЖЕНИЕ

Принцип реактивного движения: если внут

ри прочного замкнутого сосуда с отверстием

(напр., ракеты) сгорает топливо, то образо

вавшиеся сжатые газы с большой скоростью

вырываются через отверстие наружу, а кор

пус (оболочка ракеты) движется в противо

положную сторону.

Перед стартом ракеты ее общий импульс

(оболочки и топлива) в системе координат,

связанной с Землей, равен нулю. Если не

учитывать влияние силы тяжести, то кор-

пус ракеты с образовавшимися внутри него

газами можно рассматривать как замкну-

тую систему двух тел. Поэтому после запус-

ка ракеты сумма импульсов ракеты и газов

остается неизменной.

Чтобы упростить закон реактивного дви-

жения, будем предполагать, что весь газ,

образовавшийся при сгорании топлива,

выходит из ракеты не постепенно, а мгно-

венно. Поскольку до старта ракеты им-

пульс системы равняется нулю, то согласно

закону сохранения импульса и после запус-

ка он остается таким же.

Если m — масса вытекающей струи газа;



— вектор скорости струи газа; М — масса

корпуса ракеты; V



— вектор скорости кор-

пуса ракеты, то, учитывая, что скорости

газа и ракеты противоположны по направ-

лению, получим

МV



– mV



= 0.

Тогда МV



= mV



Следовательно, внутренние силы, дей-

ствующие в замкнутой системе, не могут

изменить полного импульса: какой им-

пульс получили газы в одном направлении,

такой импульс получил корпус ракеты в

противоположном направлении.

Определим скорость корпуса ракеты:

рг

= .

46.ЭНЕРГИЯИРАБОТА

В физике различаются следующие формы

движения тел (материи): механическая,

молекулярная, электромагнитная, атомная

и ядерная. Мерой различных форм движе-

ния материи является энергия, поэтому ви-

дами энергии являются: механическая,

куда входят энергии кинетическая и потен-

циальная; внутренняя, электромагнитная,

атомная и ядерная.

В процессе взаимодействия одного тела с

другим происходит передача механической

энергии. Но в процессе взаимодействия тел

может происходить преобразование одного

вида энергии в другой. Мерой передачи или

преобразования энергии является работа.

Если энергия тела, над которым соверша-

ется работа, возрастает, то величина работы

будет:

А = Е

— Е

где Е

— энергия тела до совершения над

ним работы, а Е

— энергия тела после со-

вершения работы.

47.ВЫЧИСЛЕНИЕРАБОТЫ

Элементарная работа определяется как

скалярное произведение силы F



на вектор

бесконечно малого перемещения точки Dr



под действием этой силы, т.е.

DA = F



D r



Скалярное произведение двух векторов

называется произведением модулей этих

векторов на косинус угла между ними:

DA = |



| |

D r



cos α.

Если тело движется прямолинейно, то

D r



| = DS. Тогда работа силы будет равна

D А = FDS cos α.

Если тело движется прямолинейно под

действием постоянной силы, то работа на

некотором участке пути будет равна

F(S

–

)cos α.

При α < p/2 работа силы положительна, в

этом случае проекция силы F



на направле-

ние перемещения D r



, равная F

= Fcosα,

будет совпадать по направлению с векто-

ром перемещения D r



. Тогда

A = FScosα = F

S [1 Дж = 1 Н

1 м].

При α > p/2 работа силы отрицательна.

При α = p/2 (сила направлена перпенди-

кулярно перемещению) работа силы равна

нулю.

48.РАБОТАСИЛЫТЯЖЕСТИ

Элементарная работа силы тяжести P



на

перемещение D r



будет равна

DA = P



D r



= |



| |

D r



cos α.

Сила P



направлена в сторону, противо-

положную направлению оси h, поэтому ее

проекция на h отрицательна. Выражение:

D r



cos α = Dh есть проекция перемещения

на ось h. Тогда DА = –РDh.

Если частица перемещается от точки 1 до

точки 2, то Dh = h

– h

. Тогда

A = –P(h

– h

) =

= mg(h

– h

) = mgh

– mgh

Работа силы тяжести равна произведению

силы тяжести частицы на разность ее вы

сот в начальном и конечном положениях.

49.РАБОТАСИЛЫУПРУГОСТИ

Определим вначале работу внешней силы



вн

при растяжении пружины от х

до х

Но при этом сила упругости изменяется

по закону Гука. Если в начальной точке

абсолютное значение силы было F

= Kx

то в конечной точке оно стало равным

= Kx

Тогда для вычисления работы внешней

силы нужно взять среднее значение модуля

сил F

и F

и умножить на модуль переме-

щения. Он равен |

D r



| = Dх = х

– х

Тогда

AF x

Kx Kx

вн вн.ср

−=

−

|| ()

(

∆

11212 1

)( )( )

()

=+ −=

=−=−

xxxx

Kx Kx

Тогда работа упругой силы на том же участ-

ке отличается только знаком, следовательно:

Kx Kx

упр

=−

50.МОЩНОСТЬ.КОЭФФИЦИЕНТ

ПОЛЕЗНОГОДЕЙСТВИЯ

Мощность — это работа, совершаемая в

единицу времени. Если за время t выполня-

ется работа А, то мощность определяется по

формуле

===Вт

Дж

1с

Дж/с][.1

Т.к. A = FScos α, то

FV==

cos

cos,

где α — угол между направлением силы и

скорости.

Коэф. полезного действия (КПД). Выпол-

нение работы машинами и механизмами

сопряжено с неизбежными потерями энер-

гии на преодоление сил трения. Поэтому

работу машин характеризуют с помощью

КПД, равного отношению полезной рабо-

ты А

к полной («затраченной») работе А

η= =

где N

— полезная мощность, a N

— затра-

ченная мощность.

51.ПОТЕНЦИАЛЬНАЯЭНЕРГИЯ

Пространство, в каждой точке которого

на помещенную частицу (тело) действует

сила, называется полем сил. Поле, в кото-

ром работа сил поля на пути между двумя

любыми точками не зависит от формы

пути, а зависит только от положения этих

точек, называется потенциальным, а силы

такого поля называются консервативными

(потенциальными). Если это условие не

выполняется, то силовое поле называют

диссипативным и силы такого поля называ-

ют диссипативными.

Потенциальная энергия (ПЭ) — это энер-

гия, которой обладает частица, находящая-

ся в потенциальном поле.

ПЭ систем частиц — энергия, зависящая

от взаимного расположения взаимодей-

ствующих тел или частей одного и того же

тела в потенциальном поле.

52.РАБОТАВПОТЕНЦИАЛЬНОМПОЛЕ

Для того, чтобы найти выражение ПЭ для

любого потенциального поля сил, достаточ-

но вычислить работу, совершаемую силами

поля на любом пути между двумя точками.

Именно так и было сделано при вычисле-

нии работы в однородном поле сил тяжести

и упругих сил (см. вопр. 48–49):

Amgh mghA

Kx Kx

=− =−

Из этих формул сразу видно, что ПЭ час-

тицы в силовых полях имеет следующий

вид:

•в однородном поле силы тяжести: Е

= mgh,

•в поле упругой силы

Запишем выражение работы через раз-

ность ПЭ частицы в следующем виде:

1.2

= –(Е

п2

– Е

п1

) = –DЕ

Итак, работа сил потенциального поля на

пути 12 равна убыли ПЭ, т.е. разности ее

значений в начальной и конечной точках

пути.

53.КИНЕТИЧЕСКАЯЭНЕРГИЯ

Кинетическая энергия — энергия механи-

ческого движения частицы (тела).

Сила F



, действуя на тело, совершает ра-

боту, а энергия движущегося тела возраста-

ет на величину затраченной работы. Зна-

чит, работа D А силы F



на пути DS идет на

увеличение кинетической энергии DЕ

тела, т.е.

D А = DЕ = Е

к2

– Е

к1

Итак, приращение кинетической энергии

частицы на некотором перемещении равно

работе всех сил, действующих на частицу

или систему частиц.

54.ЗАКОНСОХРАНЕНИЯЭНЕРГИИ

ВМЕХАНИКЕ

Потенциальные (консервативные) системы.

Приращение кинетической энергии систе-

мы будет равно работе, которую совершают

все силы, действующие на частицы систе-

мы. Разделив эти силы на внешние и внут-

ренние, а внутренние, в свою очередь, на

потенциальные и диссипативные, запишем

предыдущее утверждение так:

∆EA AAAA

квнешвнутр внеш внутр

пот

внутр

дис

=+=++ .

Работа внутренних потенциальных сил

равна убыли собственной потенциальной

энергии системы, т.е.

внутр

пот

=−∆ .

Тогда предыдущее выражение имеет вид:

∆∆EEAA

кпвнеш внутр

дис

+= + .

Введем понятие полной механической

энергии системы как сумму кинетической и

потенциальной энергии системы: Е = Е

+ Е

Тогда приращение кинетической энергии

и потенциальной энергии можно записать

в виде

∆EA A=+

внеш внутр

дис

Отсюда вытекает закон сохранения меха-

нической энергии: механическая энергия

замкнутой системы частиц, в которой нет

диссипативных сил, сохраняется в процессе

движения, т.е.

Е = Е

+ Е

= const.

В замкнутых консервативных системах

происходит лишь превращение потенциаль-

ной энергии в кинетическую и наоборот.

Диссипативные системы. Важной особен-

ностью диссипативных сил является то, что

суммарная работа внутренних диссипатив-

ных сил рассматриваемой системы отрица-

тельна: А

дисс

< 0.

Из этого уравнения следует, что если за-

мкнутая система не консервативна (дисси-

пативна), т.е. в ней имеются диссипатив-

ные силы, то механическая энергия такой

системы убывает:

– Е

= A

дисс

< 0.

В природе существует универсальный за-

кон сохранения энергии: энергия никогда не

создается и не уничтожается, она может

только переходить из одной формы в другую

или обмениваться между отдельными частя

ми системы.

55.КОЛЕБАТЕЛЬНОЕДВИЖЕНИЕ

Колебание — движение, при котором тело

последовательно отклоняется от положения

равновесия то в одну, то в другую сторону.

Периодические колебания, совершающи-

еся под действием сил, пропорциональных

смещению и направленных к положению

равновесия, — гармонические колебания.

Величина j = wt + j

, стоящая под знаком

косинуса (или синуса) и определяющая ве-

личину смещения точки в данный момент

времени, — фаза колебаний, j

— фаза в

начальный момент времени при t = 0. Коле-

бание, в котором смещение изменяется по

закону косинуса или синуса — гармоничес-

кое. Время, в течение которого частица со-

вершает полное колебание, — период коле-

баний Т. Частота периодических колебаний

n — число полных колебаний, которые со-

вершаются за единицу времени:

v==

1Гц].[

Циклической (круговой) частотой перио-

дических колебаний называется число

полных колебаний, которые совершаются

за 2p единиц времени:

ωπ

==2

56.УСКОРЕНИЕГАРМОНИЧЕСКОГО

КОЛЕБАНИЯ

По второму закону Ньютона F

= ma, где

а — численное значение ускорения, с кото-

рым проекция точки движется в направле-

нии оси ОХ.

Выразим F

из формулы смещения, тогда

ma = –mw

х.

Отсюда получаем численное значение ус-

корения гармонического колебания:

a = –w

х.

Значит, при гармоническом колебатель-

ном движении численное значение ускоре-

ния МТ прямо пропорционально смеще-

нию х от положения равновесия и имеет

противоположный ему знак. Уравнение для

вычисления ускорения гармонического

колебания имеет вид:

a = –w

Acos(wt + j

); a = –w

Asin(wt + j

)

или

a = w

Acos(wt + j

+ p).

Можно сделать вывод, что изменение

смещения и ускорения с течением времени

происходит с разностью фаз, равной p рад,

т.е. в противофазе. Тогда максимальное ус-

корение будет

max

= w

57.ВОЗВРАЩАЮЩАЯСИЛА

ПРИКОЛЕБАТЕЛЬНОМДВИЖЕНИИ

В колебательном движении периодически

изменяются величина и направление скоро-

сти, т.е. имеется ускорение (см. вопр. 56).

Поэтому на колеблющееся тело должна

действовать сила, сообщающая ему это ус-

корение.

Если рассмотрим равномерное вращение

с угловой скоростью w материальной точки

массой m по окружности радиуса А, то зна-

чение центростремительной силы можем

определить по формуле:

ц.с

= ma

ц.с

= mw

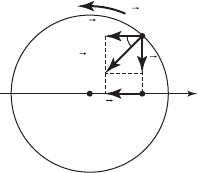
На рис. показано разложение вектора

силы F

ц.с

на две составляющие F

и F

. Под-

ставим значение центростремительной

силы в выражение проекции составляющей

силы F

на направление оси ОХ. Получим

= –F

ц.с

cosj = –mw

Acosj.

Применим формулу смещения, тогда

= F

= –mw

Acosj =

= –mw

Acos(wt + j

) = –mw

Следовательно, сила, пропорциональная

смещению МТ из положения равновесия и

направленная в противоположную сторону

(к положению равновесия), является воз-

вращающей силой.

ц.с

Здесь выражение mw

А — максимальное

значение возвращающей силы, тогда

= –F

max

cos(w t + j

)

или

= –F

max

cos(w t + j

+ p).