Автор не указан. Физика: формулы и определения: Шпаргалка

Подождите немного. Документ загружается.

11.НЕРАВНОМЕРНОЕКРИВОЛИНЕЙНОЕ

ДВИЖЕНИЕ

Неравномерное криволинейное движение —

движение, при котором частица за равные

промежутки времени совершает неодинако-

вые перемещения, двигаясь криволинейно.

В случае неравномерного криволинейно-

го движения важно знать, как изменяется

скорость с течением времени. Векторной

величиной, характеризующей быстроту из-

менения скорости по модулю и направле-

нию, является ускорение.

Среднее ускорение неравномерного дви-

жения в интервале Dt — векторная величи-

на, равная отношению изменения скоро-

сти DV



к интервалу времени D t:



ср

∆

Мгновенным ускорением МТ в момент

времени t будет предел среднего ускорения:





→

lim.

∆

Итак, мгновенное ускорение a



есть вектор

ная величина, равная пределу отношения эле

ментарного изменения скорости DV



к элемен

тарному промежутку времени Dt, или



—

производной от вектора скорости по времени.

12.РАВНОПЕРЕМЕННОЕДВИЖЕНИЕ

Равнопеременное прямолинейное движе-

ние — движение МТ, при котором скорость

ее за любые равные промежутки времени

увеличивается или уменьшается на одну и

ту же величину.

Равноускоренное движение — такое движе-

ние, при котором за любые равные проме-

жутки времени скорость возрастает на одну

и ту же величину.

Равнозамедленное движение — такое дви-

жение, при котором за любые равные про-

межутки времени скорость уменьшается на

одну и ту же величину.

Средняя скорость равноускоренного дви-

жения равна половине суммы начальной и

конечной скоростей:

ср

Из формулы ускорения (см. вопр. 10) по-

лучим мгновенную скорость:

V = V

+ at.

График скорости равноускоренного дви-

жения — прямая линия, наклонная к оси

времени, начало которой соответствует на-

чальной скорости.

Путь равноускоренного движения:

∆SVt

VVtVVatt

Vatt

ср

()()

()

000

Уравнение равнопеременного движения:

−

где S — путь.

13.СЛОЖЕНИЕУСКОРЕНИЙ

Неподвижные системы. При неравномер-

ном криволинейном движении МТ вектор

ее скорости изменяется как по модулю, так

и по направлению; имеют место ускорения

при изменении модуля скорости а

и ее на-

правления а

. Ускорение складывается по

правилу сложения векторов. Тогда резуль-

тирующее ускорение будет a



= a



+ a



Поступательно движущиеся системы. Рас-

смотрим случай, когда система Х′Y ′ переме-

щается поступательно с постоянным уско-

рением относительно системы ХY. В свою

очередь, в системе отсчета Х′Y ′ за промежу-

ток времени Dt = t

– t

скорость движения

тела изменилась от V



до V



. Скорость V



в моменты времени t

и t

в системе отсче-

та ХY, если скорость системы Х′Y ′, в свою

очередь, за это же время изменилась от V



до V



, можно найти по закону сложения

скоростей:



= V



+ V



; V



= V



+ V



Вычтем одно равенство из другого:



– V



= (V



– V



) + (V



– V



)

или



= DV



+ DV



′.

Разделим обе части равенства на проме-

жуток времени Dt, в течение которого про-

изошло изменение скорости движения тела

на DV, получим:

∆



′

В пределе при Dt → 0 будем иметь

limlim lim

∆∆ ∆

∆

rr r

→→ →

′



или

′

Окончательно:



= a



+ a



′,

где a



— ускорение системы Х ′Y ′, a



′ — ус-

корение частицы в системе Х′Y ′, a



— уско-

рение частицы в системе ХY.

Если система Х′Y ′ движется поступатель-

но с постоянной скоростью относительно

системы ХY, то a



= 0. Получим a



= a



′,

т.е. ускорение тела одно и то же в обеих

системах отсчета.

14.СВОБОДНОЕПАДЕНИЕТЕЛ

Сила тяжести — сила, с которой тела при-

тягиваются Землей.

Свободное падение тел (СП) — движение

тела под действием одной только силы тя-

жести, без учета сопротивления воздуха.

Ускорение СП. СП является равноускорен-

ным движением. Все тела независимо от

массы под действием силы тяжести падают с

одинаковым ускорением — ускорением СП,

модуль его обозначается буквой g. Ускоре-

ние СП в разных точках Земли несколько

различно и уменьшается с высотой. При

малых высотах и не очень точных измерени-

ях этой разницей можно пренебречь и счи-

тать g = 9,81 м/с

Скорость СП. Если в момент начала от-

счета времени t

= 0 тело имело скорость V

то по истечении времени t скорость тела

при СП вдоль оси OY (см. рис.) будет

V = V

+ gt. (1)

При начальной СП, равной нулю (V

= 0),

скорость тела в произвольный момент вре-

мени t будет

V = gt.

Путь при СП. В соответствии с формулой

пути равноускоренного движения путь Dh,

пройденный телом в СП, к моменту време-

ни t вдоль оси OY будет

∆hVt

Это

уравнение пути.

Уравнение движения при СП:

hh Vt

=+ +

(2)

где h

— начальная координата частицы,

a h — конечная.

Решим совместно уравнения (1) и (2) при

= 0. Значит, Dh = h. Тогда получим

−

где h — путь при СП, скорости V и V

—

проекции на ось OY.

∆h

�

15.МАССА.ПЛОТНОСТЬ

Масса — величина, равная отношению

силы к ускорению для различных тел ока-

зывается различным и является характе-

ристикой инертных свойств тела. Масса

является мерой инертности тела:

= .

Плотность вещества — это величина, из-

меряемая массой вещества в единице объ-

ема. Если масса тела m, а объем V, то плот-

ность тела

ρ=

кг/м

[].1

16.СИЛА.РАВНОДЕЙСТВУЮЩАЯ

Сила — это векторная величина, явля-

ющаяся мерой механического воздействия

на тело со стороны других тел или полей, в

результате которого тело приобретает уско-

рение или изменяет свою форму и размеры.

Сила — это мера взаимодействия тел или

частиц, из которых состоит тело.

Равнодействующая сила — результиру-

ющая сила, результат сложения всех сил,

действующих на тело. Равнодействующая

сила равна диагонали параллелограмма,

стороны которого являются слагаемыми

силами:



= F



+ F



При сложении нескольких сил



∑

где R



— равнодействующая сила, n — кол-

во действующих сил.

17.СЛОЖЕНИЕСИЛ

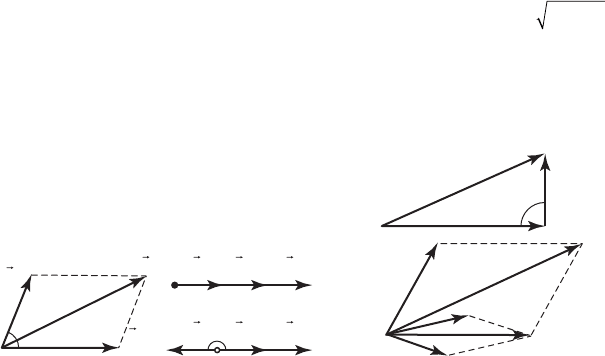
Сложение сил, направленных под углом друг к

другу (рис. 1). Сложение сил по правилу па-

раллелограмма — геометрическое сложение.

Геометрическая сумма зависит от модулей

слагаемых сил и угла между ними. Модуль

равнодействующей F



двух сил F



и F



, на-

правленных под произвольным углом α друг

к другу, определяется по теореме косинусов:

= F

+ F

+ 2F

cos α.

Сложение сил, действующих вдоль прямой

линии. Равнодействующая двух сил, на-

правленных вдоль одной прямой в одну

сторону и имеющих одинаковое направле-

ние (α = 0), равна по величине сумме моду-

лей составляющих сил и направлена в ту же

сторону (рис. 2).

Равнодействующая двух сил, направлен-

ных вдоль одной прямой в противоположных

направлениях (α = 180°), равна модулю раз-

ности численных значений слагаемых сил и

направлена в сторону большей силы (рис. 3).

18.СЛОЖЕНИЕСИЛ(ПРОДОЛЖЕНИЕ)

Сложение двух сил, направленных под пря-

мым углом. Равнодействующая двух сил,

направленных под прямым углом друг к

другу (α = 90°) согласно рис. 1, по модулю

определяется теоремой Пифагора: квадрат

гипотенузы равен сумме квадратов катетов:

= F

+ F

. Тогда

FFF=+

Сложение нескольких сил, больше двух,

можно производить по правилу параллело-

грамма (рис. 2). При этом в качестве одной из

слагаемых сил рассматривается полученная

перед этим равнодействующая сила



∑

�

+ F

�

Рис. 1

Рис. 2

Рис. 3Рис. 1

19.ПЕРВЫЙЗАКОННЬЮТОНА

(ЗАКОНИНЕРЦИИ)

Первый закон Ньютона: всякое тело сохра

няет состояние покоя или равномерного и

прямолинейного движения до тех пор, пока

на него не действует сила или действие всех

сил скомпенсировано. Закон записывается в

виде формулы:

∑

где S — знак суммы, a n — кол-во действу-

ющих сил.

Инерция — св-во тел сохранять состояние

покоя или равномерного прямолинейного

движения. Первый закон Ньютона называ-

ют также законом инерции.

Инерциальные системы — системы отсче-

та, в которых выполняется первый закон

Ньютона. Система отсчета, в которой он не

выполняется, называется неинерциальной

системой отсчета.

Инертность — св-во тел получать различ-

ные ускорения при действии на них одина-

ковой по величине и направлению силы.

Чем больше ускорение получает тело, тем

меньше его инертность, и наоборот.

20.ВТОРОЙЗАКОННЬЮТОНА

Второй закон Ньютона: ускорение — век

торная величина, поэтому сила должна быть

векторной величиной. Можно записать:



Fma==⋅=

⋅













1Н кг 1м/с

кг м

Ускорение прямо пропорционально силе,

действующей на тело, и обратно пропорци-

онально массе тела:



= .

Если на тело действует несколько сил, то

ma F



∑

где знак S выражает сумму, a n — кол-во

действующих сил.

21.ТРЕТИЙЗАКОННЬЮТОНА

Опыт показывает, что при любом взаимо-

действии двух тел, массы которых равны m

и m

, отношение модулей их ускорений ос-

тается постоянным и равным обратному

отношению масс тел:

am am

11 22

==или.

Векторный вид этого уравнения: m



= –m



. Знак «минус» выражает тот опыт-

ный факт, что при взаимодействии тел их

ускорения всегда имеют противоположные

направления.

Исходя из второго закона Ньютона, полу-

чаем равенство



= –F



Это выражение называется третьим зако-

ном Ньютона: силы, с которыми две МТ

действуют друг на друга, всегда равны по

величине и направлены в противоположные

стороны вдоль прямой, соединяющей эти

точки, т.е. F



1.2

= –F



2.1

, где F



1.2

— сила дей-

ствия частицы т

на частицу m

, a F



2.1

—

сила действия частицы m

на частицу m

22.СКОРОСТЬПРИДВИЖЕНИИ

ПООКРУЖНОСТИ

Период Т — это время, в течение которого

частица совершает один оборот, двигаясь

по окружности. Частота n — это количество

оборотов, совершаемых частицей в едини-

цу времени при движении по окружности.

Скорость, с которой частица движется по

окружности, — линейная скорость.

Если частица при равномерном движе-

нии по окружности за время, равное пери-

оду t = T, делает один оборот, то она прохо-

дит путь, равный длине окружности S = 2pr,

поэтому модуль линейной скорости будет

T==

21π

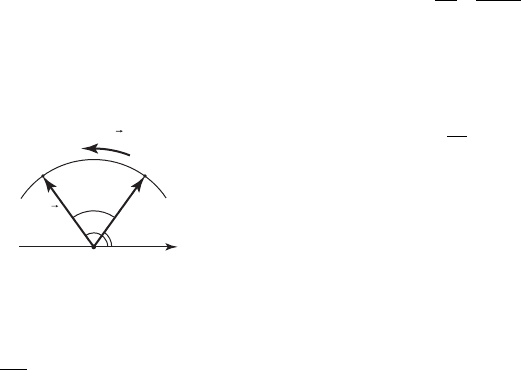
23.ДВИЖЕНИЕПООКРУЖНОСТИ:

УГЛОВОЙПУТЬ,УГЛОВАЯСКОРОСТЬ

Угловой путь. Проведем радиус-вектор r



, со-

единяющий центр окружности с МТ А, дви-

жущейся по окружности. Укажем углом j

отсчитывая от оси ОХ до радиус-вектора r



против часовой стрелки, начальное положе-

ние, а углом j — конечное положение час-

тицы (см. рис.). Изменение положения час-

тицы по окружности может быть охарактери-

зовано изменением ее угловой координаты

Dj = j – j

, где Dj — угол поворота радиус-

вектора частицы — угловой путь.

A A

Δϕ

Угол поворота можно выражать в градусах.

В СИ за единицу угла принят радиан (рад) —

угол между двумя радиусами окружности,

длина дуги между которыми равна радиусу.

2πr

= 2p рад, 2p рад = 360°.

Угловая скорость w измеряется углом пово-

рота радиус-вектора (угловым путем) в еди-

ницу времени, т.е. отношением углового пути

Dj к промежутку времени Dt, за который

этот путь пройден; угловая скорость равна:

ϕϕ

−

∆

∆ttt

Если частица при равномерном враще-

нии совершает полный оборот по окруж-

ности, то численная величина угловой

скорости принимает вид

πν==

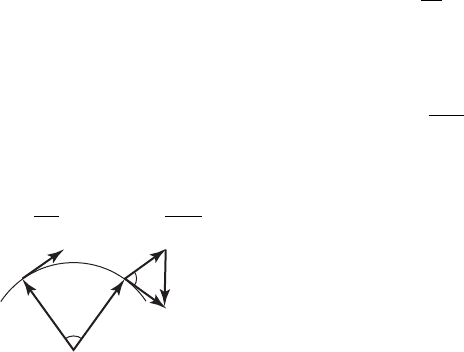
24.УСКОРЕНИЕПРИДВИЖЕНИИ

ПООКРУЖНОСТИ

Линейная скорость равна угловой скоро-

сти, умноженной на радиус: V = w r. По-

скольку направление вектора линейной

скорости V



изменяется, то существует ус-

корение. Определим это ускорение.

За малый промежуток времени Dt МТ А

проходит небольшой путь D S, равный дуге

центрального угла Dj (см. рис.). При этом

скорость V



получит приращение DV



, что

вызывает изменение ее направления на

угол Dj. При равномерном движении час-

тицы приращения скорости за равные про-

межутки времени будут постоянными, тог-

да ускорение равно:

===

∆

∆∆

∆

,.ϕ

∆ϕ

�

∆V

�

∆S

25.ЦЕНТРОСТРЕМИТЕЛЬНАЯСИЛА

При равномерном движении частицы по

окружности возникает центростремитель-

ное ускорение:

ц.с

== =

222

4ωπν .

На основании второго закона Ньютона

соответствующая центростремительная

сила будет равна

Fma

mRmr

ц.сц.с

====

222

4ωπν .

Центростремительная сила удерживает

движущееся тело на окружности, приложе-

на к этому телу и направлена по радиусу к

центру окружности. Эта сила — результат

воздействия удерживающего тела на вра-

щающееся тело.