Astakhov V. Tribology of Metal Cutting

Подождите немного. Документ загружается.

Basics, Deﬁnitions and Cutting Tool Geometry 407

kind as well as local and global interference are considered. The interference mentioned

can result in interference mark on the tool body, at the best, or it leads to rapid tool

damage and makes the cutting operation impossible.

A3.4 Cutting edge radius

As discussed above, the tool designer apparently has the rake and the ﬂank angle design

parameters to optimize the tool performance. Practice of tool production, however, proves

that this is not always the case.

The problem is that the edge is assumed to be very sharp compared to the thickness of the

layer to be removed and, therefore, the actual rake angle is the same as that assigned by

the tool drawing. This is true for more than 80% of the metalworking operations, where

the thickness of the layer to be removed is 10–20-fold greater than the radius of the

cutting edge. As such, this radius is simply neglected and the cutting tool is considered

to be perfectly sharp. Unfortunately, the same cannot be applied to many ﬁnishing and

hard turning operations with a very “light” uncut chip thickness. One may wonder: what

seems to be the problem?

To understand the problem, consider the model of cutting shown in Fig. 3.46 (Chapter 3),

where a cutting tool having a radius of the cutting edge ρ

is shown. The tool is set to

remove the uncut chip thickness t

. Due to the radius of the cutting edge, this uncut chip

thickness is divided into two parts: the actual uncut chip thickness t

, which is removed

by cutting and thus turns into the chip, and the deformed uncut chip thickness h

which is

ploughed under the tool. When the ratio t

/ρ

≥ 10, the effect of ρ

is small so the tool is

considered to be perfectly sharp. However, when t

/ρ

< 10, the relative impact due to

ploughing by the rounded cutting edge becomes signiﬁcant and thus cannot be ignored.

Naturally, the cutting process ceases at certain t

/ρ

turning to be pure burnishing or

ploughing.

It is discussed in Chapter 3 that the cutting process ceases and the layer to be removed

undergoes plastic deformation similar to burnishing when (Eq. (3.69))

≤ 0.5 −

, (A19)

where σ

is the yield strength of the work material and τ

is the shear strength of adhesion

bonds between work and tool materials.

The shear strength of adhesion bonds primarily depends on the mechanical properties of

the work material and the contact temperature.

Equation (A19) allows us to determine the limiting uncut chip thickness (t

1−lim

= h

)

for a given combination of work and tool materials. However, one should note that the

cutting process becomes unstable even before this limiting value is reached. It can be

easily detected by excessive vibrations, poor surface ﬁnish and reduced tool life.

408 Tribology of Metal Cutting

Example 2

Problem: Determine the minimum feed that can be used in the machining of 303

stainless steel with the depth of cut t

= 2 mm by a carbide insert KC850 (Kennametal)

having the cutting edge angle κ

= 72

◦

, nose radius r

= 0.8 mm and cutting edge radius

= 0.055 mm.

Solution: For the steel considered τ

= 145 MPa and σ

= 264 MPa. From Eq. (A19),

the limiting uncut chip thickness is calculated as

1−lim

= ρ



0.5 −



= 0.055



0.5 −

145

264



= 0.025 mm

Given conditions indicate that we deal with the case shown in Fig. A7(a). Therefore,

we can calculate the critical cutting feed using iteration method for Eq. (A8)

= t

1−lim

sin arctan

(

([

1 − e

(1 − cos κ

)

]

cot κ

(sin κ

)

))

= 0.025 ×c

sin arctan

[

1 − 0.4(1 − cos 72)

]

cot 72 +0.4(sin 72 +g

)

where

2 × 0.8

0.8

= 0.4 and

= 1 −e



1 −



1 − g



= 1 −0.4



1 −



1 − g



The minimum cutting feed f

= 0.039 mm/rev was calculated using MathCAD.

To verify that the case considered corresponds to Fig. A7(a), we can check the conditions

set by Eq. (A7)

= 2 ≥ r

(

1 − cos κ

)

= 0.8



1 − cos 72

◦



= 0.55 : valid

= 0.039 ≤ 2r

sin κ

= 2 ×0.8 ×sin 72 = 1.52 : valid

A3.5 Inclination angle

Although the sense and sign of the inclination angle λ

is clearly shown in Fig. A4

and it is deﬁned earlier as the angle between the cutting edge and the reference plane,

experience shows that there are certain difﬁculties and confusions in understanding this

angle.

Figure A11 aims to clarify the issue. The inclination angle λ

is measured in a plane

H which is perpendicular to the reference plane xy and passes through the tool tip

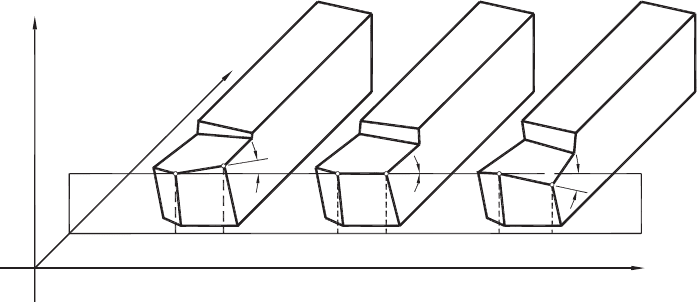
Basics, Deﬁnitions and Cutting Tool Geometry 409

−l

= 0°

Fig. A11. Sense of the sign of the inclination angle.

(nose point) 1. Numbers 1 and 2 designate the ends of the cutting edge. As such, if

the tool tip 1 is located below point 2, the inclination angle λ

is positive; if points 1 and

2 are at the same level, λ

= 0; and when the tool tip 1 is located above point 2, then

the inclination angle λ

is negative.

The sign of the inclination angle deﬁnes the chip-ﬂow direction, as shown in Fig. A12.

When λ

is positive, the chip ﬂows to the right and when λ

is negative, the chip ﬂows

to the left. The direction of chip ﬂow, however, is deﬁned not only by λ

, but also by

the cutting edge angle κ

. These two angles deﬁne the spatial location of the tool cutting

edge. In turn, the spatial location of the cutting edge constrains the location of these

planes, since the cutting edge is the line of intersection of the rake and ﬂank planes.

The complete location of the rake plane is then deﬁned when the normal rake angle γ

is known and the location of the ﬂank planes is fully deﬁned when the normal ﬂank

angle α

is known.

Simple relationships exist among the angles considered in the tool-in-hand system. These

relationships have been derived assuming that the tool-side rake angle γ

, the tool-back

rake angle γ

and the tool cutting edge angle κ

are the basic angles for the tool face, and

the tool side clearance angle α

, the tool back clearance angle α

, and the tool cutting

edge angle κ

are the basic angles for the tool ﬂank

tan λ

= sin κ

tan γ

−cos κ

tan γ

(A20)

tan γ

= cos λ

tan γ

(A21)

tan γ

= cos κ

tan γ

+sin κ

tan γ

(A22)

cos α

= cos λ

cot α

(A23)

cot α

= cos κ

cot α

+sin κ

cot α

(A24)

410 Tribology of Metal Cutting

−l

Fig. A12. Inﬂuence of sign of the inclination angle on the direction of chip ﬂow.

It must be stated, however, that some of these relationships apply only when the cutting

edge angle κ

is less than 90

◦

. Nowadays, it is a common practice to use cutting tools

having κ

greater than 90

◦

. Moreover, most of the drills are made in the same way.

For these tools, the following relationships are valid

tan λ

=−sin κ

tan γ

−cos κ

tan γ

(A25)

tan γ

= cos λ

tan γ

(A26)

tan γ

=−cos κ

tan γ

+sin κ

tan γ

(A27)

cot α

= cos λ

cot α

(A28)

cot α

=−cos κ

cot α

+sin κ

cot α

(A29)

A4 Determination of Uncut Chip Thickness for a General Case

Section A3 deﬁnes the uncut chip thickness for the simplest case where a single-point

cutting tool is used for turning (Fig. A7). Because the uncut chip thickness deﬁnes to a

large extent the tribological conditions of any cutting operation, its proper determination

for the whole variety of the cutting tools should be provided. Unfortunately, none of

the books contains such a material, and so tool designers, manufacturing specialists and

practitioners in the ﬁeld have no reference to turn to in the determination of uncut chip

thickness for many cutting operations besides turning, milling and drilling. As a result,

the determination of the true uncut chip thickness is not carried out in the design and

analysis of many tools.

Further considerations are based on the method proposed by Rodin [6] and further

developed by Astakhov et al. [7,8].

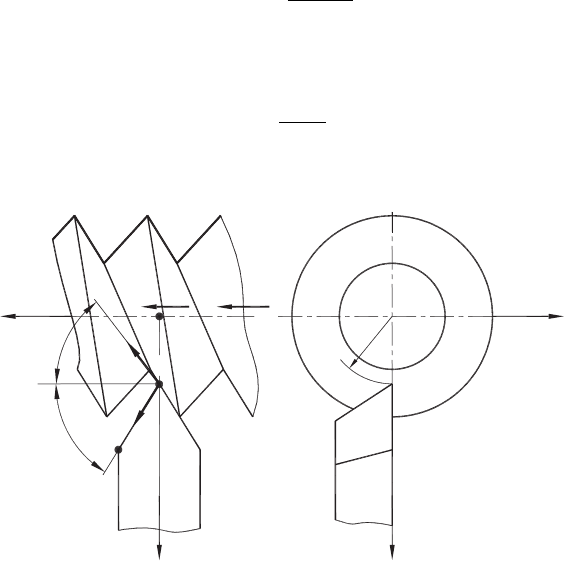
Basics, Deﬁnitions and Cutting Tool Geometry 411

The uncut chip thickness for any machining operation at a given point of the cutting

edge is determined as

= f cos χ

, (A30)

where χ

is the angle between the feed direction and the normal to the tool cutting edge

plane at the point of the cutting edge considered. This angle can be considered as the

tool cutting edge angle in the tool-in-use system.

Generally, angle χ

is considered in the 3D plane containing the vectors of the feed

motion and the normal to the tool cutting edge plane at the point considered. Note that

this plane is always the main reference plane in the tool-in-use system of consideration

of the tool geometry. The direction of feed for a tool working with several feed motions

is determined by the vector summation of the directions of all these feeds. This should

not present any problem as these directions are well known.

As angle χ

is between the feed direction f and the normal N to the tool cutting edge

plane at the point of the cutting edge considered, the angle between these two vectors is

determined as

cos χ

f × N







(A31)

and thus the uncut chip thickness is then calculated as

f × N



(A32)

Fig. A13. Determining the uncut chip thickness in thread cutting.

412 Tribology of Metal Cutting

Consider the determination of the uncut chip thickness t

in a thread-cutting operation

as an example of the use of the proposed methodology. A model of this operation is

shown in Fig. A13. A thread cutting is fed incrementally after each pass by feed f in the

direction of f so the cutting edge AB does the entire cutting. In this model, vector a is a

unit vector along the cutting edge so it always lies in the tool cutting edge plane in any

system of consideration. The xyz coordinate system is set, as shown in Fig. A13. In this

coordinate system, the vector of the cutting feed f is determined by its projection on the

corresponding coordinate axes as

f = if cos δ

−jf sin δ

(A33)

and unit vector a as

a = i cos κ

+j sin κ

(A34)

If R

is the location radius of point A of the cutting edge, the velocity of this point in its

spiral motion is

= iν

+ω × R

= iν

+kωR

, (A35)

where ν

is the velocity of the tool in the x direction. It is understood that

= knp, (A36)

where k is the number of starts of the thread being cut, n is the number of revolutions

per second of the vortices (rpm/60) and p is the thread pitch.

A normal S to the tool cutting edge plane in the tool-in-use system is determined by the

cross product of vectors v

and a located in this plane as

N = a ×v

ijk

cos κ

sin κ

0 ωR

= iωR

sin κ

+jωR

cos κ

−kν

sin κ

(A37)

and its modulus



= ω



sin

, (A38)

where h

= ν

/ω is the helix parameter.

Using Eq. (A32), one can obtain

ωR

sin κ

cos δ

+ωR

f cos κ

sin δ



sin



+δ





sin

(A39)

Basics, Deﬁnitions and Cutting Tool Geometry 413

As shown, the uncut chip thickness varies along the cutting edge because radius R

differs for each of its point. In a particular case of bar turning, δ

= 0 and h

= 0, thus

Eq. (A39) becomes

= f sin κ

(A40)

which is the same as Eq. (A3) obtained earlier for this case.

References

[1] Astakhov, V.P., Metal Cutting Mechanics, CRC Press, Boca Raton, USA, 1998.

[2] Oxley, P.L.B., Mechanics of Machining: An Analytical Approach to Assessing Machinability,

John Wiley & Sons, New York, USA, 1989.

[3] Klushin, M.I., Metal Cutting: Basics of Plastic Deformation of the Layer Been Removed,

Mashgiz, Moscow, Russia, 1958.

[4] Stabler, G.V., The chip ﬂow law and its consequences. In Proceedings of the 5th International

MTDR Conference, 1964.

[5] Colwell, L.V., Predicting the angle of chip ﬂow for single point cutting tools, Transactions

of the ASME, 76 (1954), 199–202.

[6] Rodin, P.R., The Basics of Shape Formation by Cutting (in Russian), Visha Skola, Kyev,

Ukraine, 1972.

[7] Astakhov, V.P., Galitsky, V.V., Osman, M.O.M., A novel approach to the design of self

piloting drills. Part 1. Geometry of the cutting tip and grinding process, ASME Journal of

Engineering for Industry, 117 (1995), 453–463.

[8] Astakhov, V.P., Galitsky, V.V., Osman, M.O.M., A novel approach to the design of

self-piloting drills with external chip removal. Part 2: Bottom clearance topology and

experimental results, ASME Journal of Engineering for Industry, 117 (1995), 464–474.

APPENDIX B

Experimental Determination of the Chip

Compression Ratio (CCR)

B1 General Experimental Techniques

Although a number of experimental methods for the determination of the chip compres-

sion ratio (CCR) were known to researchers, modern books and other publications on

metal cutting do not consider any of them because CCR is not regarded as an important

parameter in metal cutting studies. Because it is argued in this book that major tribologi-

cal parameters and characteristics of metal cutting correlate with CCR, a need to present

a few common experimental methods for the determination of CCR is felt.

The simplest method is to measure the chip thickness and then calculate CCR as

ζ = t

, (B1)

where t

is the chip thickness and t

is the uncut chip thickness.

However this is not always possible because the chip: (a) might have a saw-toothed free

surface and (b) be very small and 3D-curved.

The second method is the weighing method. A small (5–10 mm long) straight piece of

the chip is separated from the rest of the chip. Then, its length L

and width d

are

measured. When the piece of the chip selected for the study is not straight, a computer

vision system available nowadays in most shops is used to measure its length properly.

Then, it is weighed so its weight G

(N) is determined. The chip thickness is then

calculated as

, (B2)

where ρ

is the density of the work material (kg/m

) and g = 9.81 m/s

is the gravity

constant.

414

Experimental Determination of the Chip Compression Ratio (CCR) 415

For ﬁnishing operations when the depth of cut is shallow, it becomes rather difﬁcult to

measure the width of the chip. CCR is determined in this case using the ratio of the chip

and the uncut chip cross-sectional areas, A

and A

, respectively, i.e.

ζ =

(B3)

As such, the cross-sectional area of the chip is determined using the weighing method as

(B4)

and the cross-sectional area of the uncut chip is determined as

= d

f, (B5)

where d

is the depth of cut and f is the cutting feed.

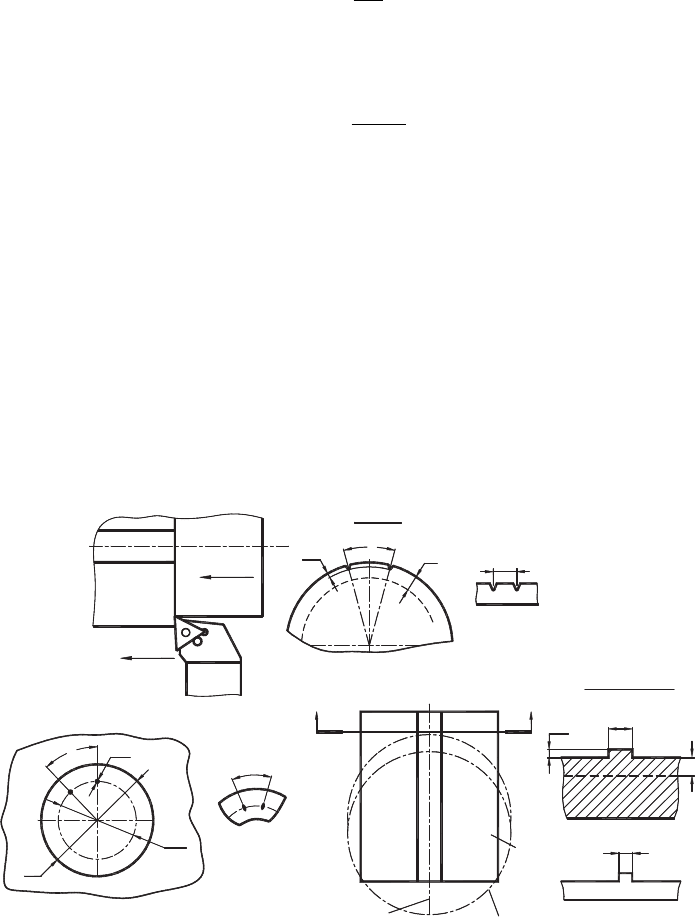
The third method is the direct method, which is applicable in turning, milling, drilling and

other common machining operations. The essence of this method is that the workpiece

is “marked” before cutting and then the resultant marks on the chip are compared with

the original marks. The realization of this method for longitudinal turning is shown in

Fig. B1(a). As shown, two longitudinal grooves are made on the outer surface of the

Tool

Fragment of the chip

ØD

Ød

Workpiece

Ød

(b) DRILLING

Trajectory of cutters

Axis of the tool

Fragment of the chip

Workpiece

SECTION A-A

Workpiece

Fragment of the chip

(a) TURNING

Workpiece

View A

Fig. B1. Practical methods of determining CCR.

416 Tribology of Metal Cutting

workpiece before testing and the arc distance between these grooves L

is measured.

After the test, a chip section with these marks can be easily found and the distance L

is measured. CCR is then determined as

ζ = L

(B6)

The realization of the method discussed to measure CCR in drilling is shown in

Fig. B1(b). Two small holes of diameter d

are drilled as shown in Fig. B1(b) along

the trajectory of the point of the drill cutting edge. Diameter d

is smaller than that (D)

of the would-be-hole. The arc distance L

between the centers of these holes is mea-

sured. After the test, a chip fragment having marks from the two holes is found and the

arc distance L

between their centers is measured at high magniﬁcation using an optical

comparator or a computer vision system. Using Eq. (B6), CCR is determined.

The realization of the discussed method for face milling is shown in Fig. B1(c). As

shown, the surface of the workpiece is made with a step having width L

=3–6 mm

and height which is 4–6 times smaller that the depth of the cut, i.e. d

= 4–6. After

the test, the width L

is measured and CCR is determined using Eq. (B6). Shifting the

position of the axes of the tool and the workpiece, one can determine CCR under a wide

range of uncut chip thickness.

B2 Design of Experiment

Approximation of the dependence of CCR on the factor “vt

” (the Peclet criterion) can

be accomplished using a simple test program consisting of only two runs. For example,

for the test results of which shown in Fig. 2.8, the following simple design of experiment

can be utilized. Table B1 shows the plan of tests.

Using these test results, CCR can be approximated as follows:

ζ = ζ



√

(

)

(

)



, (B7)

where



√

2.60 × 1.93 = 2.24 (B8)

Table B1. Plan and test results.

Test number (i) 10

/s) CCR (ζ

)

1 0.25 2.60

2 1.85 1.93