ASME Section VIII div 2 2010. ASME Boiler and Pressure Vessel Code. Alternative Rules

Подождите немного. Документ загружается.

2010 SECTION VIII, DIVISION 2

5-89

5.D.3 Stress Indices for Laterals

5.D.3.1 The stress indices for laterals in cylindrical shells in Table 5.D.3 may be used when all of the

following conditions are satisfied:

a) The angle

equals 45 deg; these indices may be used for angles of

less than 45 degrees (see

Figure 5.D.3).

b) The nozzle is of circular cross section and has an axis that intersects the axis of the cylindrical vessel.

c) The design of the nozzle reinforcement is in accordance with the applicable rules of paragraph 4.5.

d) The following dimensional ratios are satisfied.

40.0

≤

(5.D.11)

0.5

≤

(5.D.12)

3.0

≤

(5.D.13)

e) The nominal pressure membrane stress to be used with the pressure indices is determined using the

following equations.

()

(12)

PD t

or Regions and

(5.D.14)

()

(3)

ni p

Pd t

or Region

(5.D.15)

5.D.3.2 Stress indices for laterals in cylindrical shells may be developed by stress analysis techniques

consistent with the elastic design analysis methods of Part 5, or obtained for other sources.

2010 SECTION VIII, DIVISION 2

5-90

5.D.4 Nomenclature

D inside vessel diameter.

d inside nozzle diameter.

pressure.

r local nozzle radius, see Figure 5.D.2.

stress component normal to the boundary of the section.

stress component in the plane of the section under consideration and parallel to the boundary

of the section.

stress component normal to the plane of the section (ordinarily the circumferential stress

around the hole in the shell.

t minimum wall thickness in the region under consideration, or the thickness of the vessel, as

applicable.

t thickness of perforated plate, or the thickness of the pipe portion of a nozzle, as applicable.

angle between the axis of the nozzle and the normal to the vessel.

标准分享网 www.bzfxw.com 免费下载

2010 SECTION VIII, DIVISION 2

5-91

5.D.5 Tables

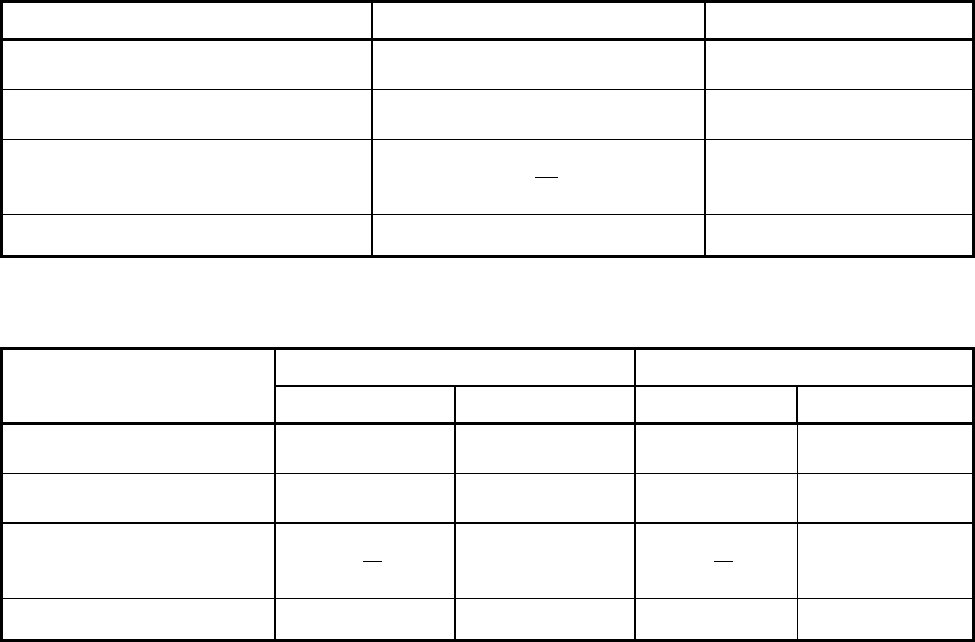
Table 5.D.1 – Stress Indices For Nozzles In Spherical Shells And Portions Of Formed Heads

Stress Inside Corner Outside Corner

2.0 2.0

0.2

−

2.0

−

0.0

2.2 2.0

Table 5.D.2 – Stress Indices For Nozzles In Cylindrical Shells

Material Longitudinal Plane Transverse Plane

Inside Corner Outside Corner Inside Corner Outside Corner

3.1 1.2 1.0 2.1

0.2

−

1.0

0.2

−

2.6

−

0.0

−

0.0

3.3 1.2 1.2 2.6

2010 SECTION VIII, DIVISION 2

5-92

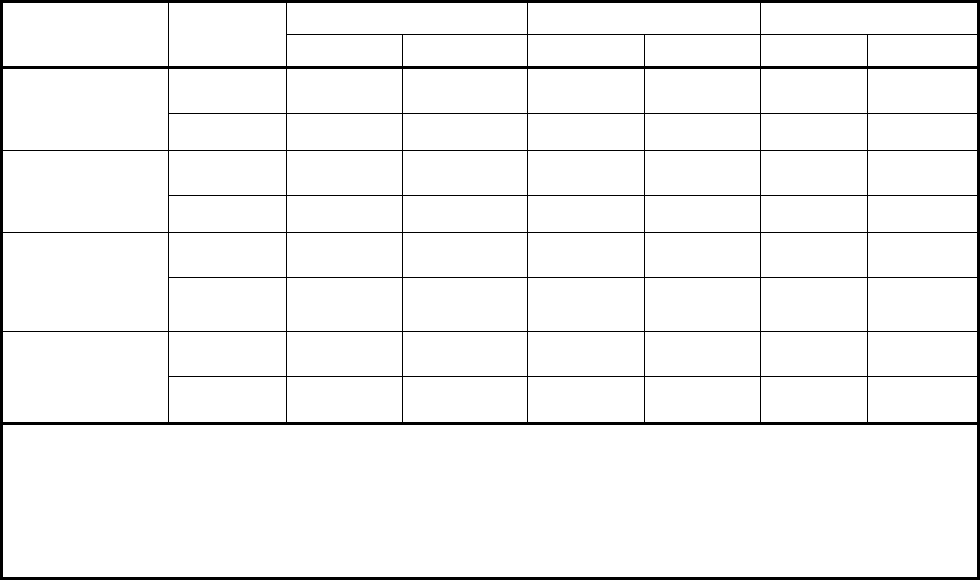
Table 5.D.3 – Stress Indices For Laterals

Load Stress Region 1 Region 2 Region 3

Inside (1) Outside (1) Inside Outside Inside Outside

Pressure

max

5.5 0.8 3.3 0.7 1.0 1.0

5.75 0.8 3.5 0.75 1.2 1.1

In-Plane Branch

Moment,

max

0.1 0.1 0.5 0.5 1.0 1.6

Vessel

Moments,

max

2.4 2.4 0.6 1.8 0.2 0.2

2.7 2.7 0.7 2.0 0.3 0.3

Out-Of-Plane

Branch

Moment,

max

0.13 NA 0.06 NA NA 2.5 (2)

0.22 NA 0.07 NA NA 2.5 (2)

Notes:

1. Inside/outside refers to inside corner (pressure side)/outside fillet and in the plane of symmetry as

shown in Figure 5.D.3

2. Maximum stress/stress intensity in Region 3 for transverse moment

occurs 90

away from in-

plane moment.

标准分享网 www.bzfxw.com 免费下载

2010 SECTION VIII, DIVISION 2

5-93

5.D.6 Figures

Figure 5.D.1

Direction of Stress Components

2010 SECTION VIII, DIVISION 2

5-94

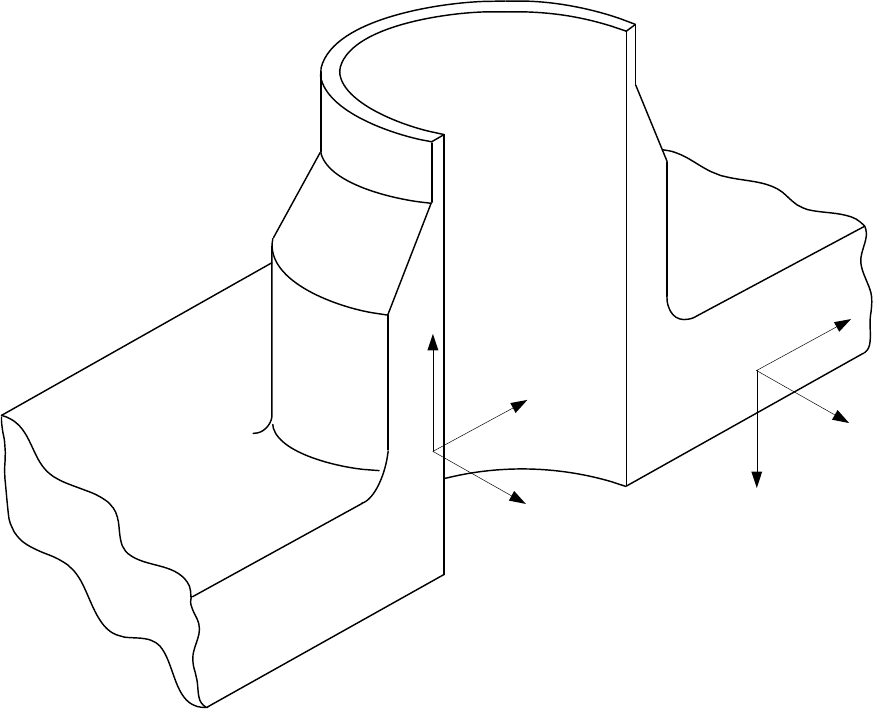
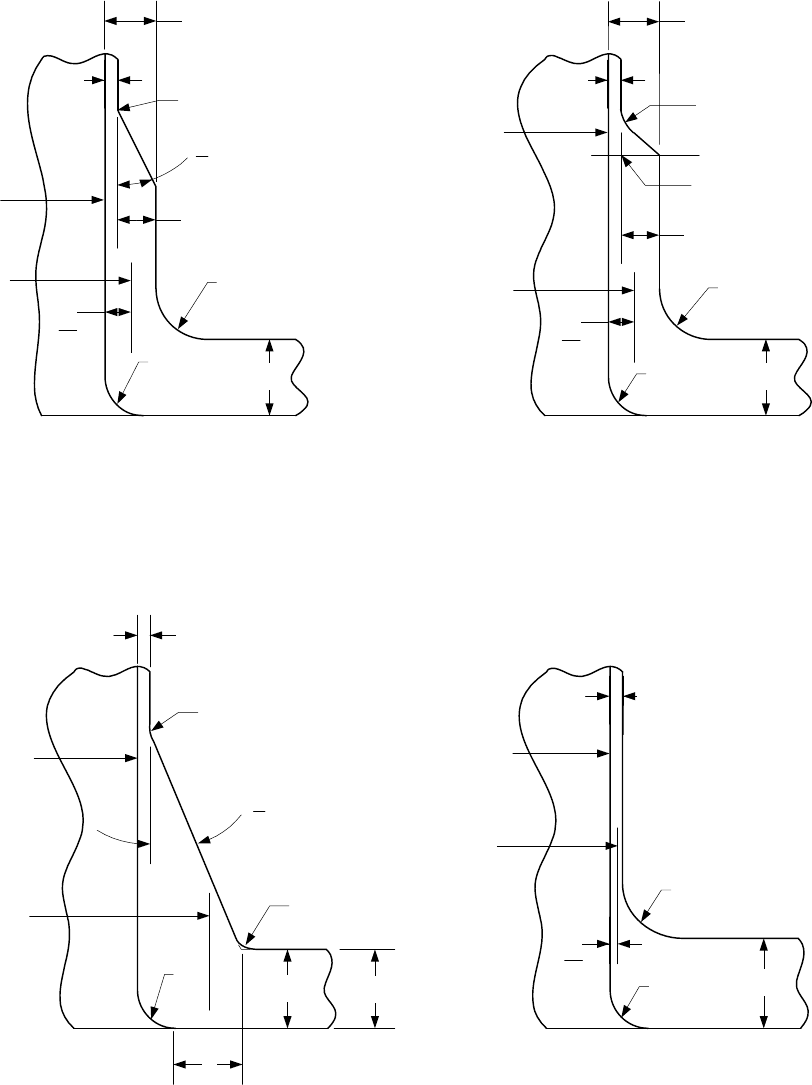
Shell Thickness

= r + 0.5t'

= t

+ 0.667x

θ < 45°

Offset

θ = 90°

, t

Figure 5.D.2

Nozzle Nomenclature and Dimensions

标准分享网 www.bzfxw.com 免费下载

2010 SECTION VIII, DIVISION 2

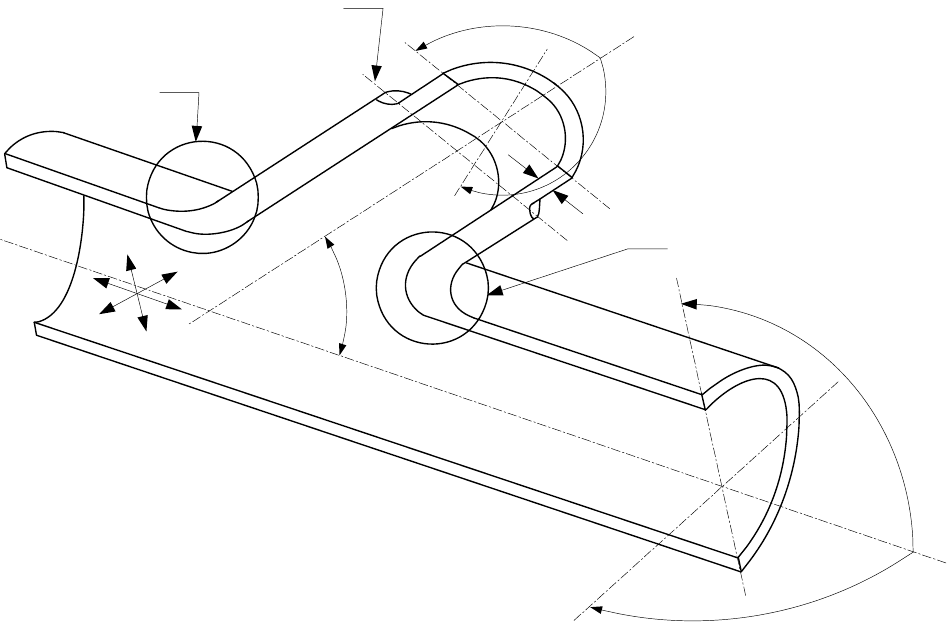
5-95

Region 1

Region 3

Region 2

Figure 5.D.3

Nomenclature and Loading for Laterals

2010 SECTION VIII, DIVISION 2

5-96

ANNEX 5.E

DESIGN METHODS FOR PERFORATED PLATES BASED ON

ELASTIC STRESS ANALYSIS

(NORMATIVE)

5.E.1 Overview

5.E.1.1 This paragraph contains a method of analysis for flat perforated plates subjected to applied loads or

loadings resulting from structural interaction with adjacent members. This method applies to perforated plates

that satisfy the following conditions:

a) The holes are in an equilateral triangular or square penetration pattern.

b) The holes are circular and the axis of the hole is perpendicular to the surface of the plate.

c) There are 19 or more holes.

d) The effective ligament efficiency satisfies the following criteria in paragraph 5.E.4.

5.E.1.2 Rolling or pressure expansion of tubes into a tubesheet will result in compression on the inside

diameter of the tubesheet perforation and the tube itself. Thermal transients that occur during operation may

result in thermal differential between the tube and the tubesheet resulting in a loss of the compression

obtained during fabrication. For tubes that are also welded, such thermal cycling can cause fatigue of the

weld joining the tube to the tubesheet. For tubes that are not welded, thermal cycling can cause the tube to

loose contact resulting in leakage. A transient thermal and stress analysis can determine the magnitude of

cyclic stress in the tube weld. For small ligaments, the pressure expansion of tubes can cause significant

ligament deformation and stresses.

5.E.2 Stress Analysis of the Equivalent Solid Plate

5.E.2.1 The analysis method for perforated plates presented in this paragraph is based on the concept of an

effective solid plate. In this method, the material properties of the actual perforated plate are replaced by

material properties of an effective solid plate that approximate the stiffness of the actual perforated plate. A

stress analysis is then performed where the effective solid plate is used in the model that is geometrically

similar to the perforated plate, and subject to the actual loading conditions. After completion of the stress

analysis, the values of the stresses in the actual perforated plate are obtained by applying stress multiplying

factors to the stress results computed for the effective solid plate.

5.E.2.2 An accurate model of the overall tubesheet behavior may be achieved by employing the concept of

an equivalent elastic material of anisotropic properties. For triangular penetration patterns the in-plane

behavior of the tubesheet is isotropic and the anisotropy of the equivalent material must only be considered

for stresses in the thickness direction. The tubesheet can be analyzed using an axisymmetric solid numerical

analysis with the effective elastic matrix

[]

to simulate the anisotropic behavior. For square penetration

patterns the equivalent material properties depend on the orientation of the loading with respect to the

symmetry axes of the pattern. The tubesheet can be analyzed using an axisymmetric solid numerical

analysis with the effective average elastic matrix

[]

for in-plane loading to simulate the anisotropic behavior.

When the tubesheet loading is not axisymmetric (e.g. channels with divider plates), a three-dimensional solid

numerical analysis may be required.

标准分享网 www.bzfxw.com 免费下载

2010 SECTION VIII, DIVISION 2

5-97

5.E.3 Stiffness Effects of the Tubes

5.E.3.1 The in-plane stiffening effect of the tubes in the perforations may be included in the analysis. The

extent to which the tubes stiffen the perforated plate depends on the materials, the manufacturing processes,

operating conditions, and degree of corrosion. This stiffening effect may be included in the calculations by

including part or all of the tube walls in the ligament efficiency used to obtain the effective elastic constants of

the plate. Such stiffening may either increase or decrease stresses in the plate itself and in the attached

shells.

5.E.3.2 Where applicable, the stiffening effect resulting from the staying action of the tubes should be

incorporated into the numerical analysis. For fixed-fixed type exchangers, the axial stiffness of the tubes shall

be included in the analysis. When including the tube stiffness, the difference in axial strain due to pressure

between the shell and tubes (Poisson’s effect) as well as differential thermal expansion between tubes and

shell should also be included in the numerical analysis.

5.E.4 Effective Material Properties for the Equivalent Solid Plate

5.E.4.1 The effective elastic constants of the perforated plate are determined as a function of the effective

ligament efficiency

that is computed in accordance with paragraph 4.18.6.4.

5.E.4.2 If the hole pattern is irregular or has isolated thin ligaments in a uniform hole pattern, the calculated

elastic constants shall represent the average ligament size over the entire modeled plate in order to capture

the global response. The stress multipliers used for the fatigue assessment of paragraph 5.E.7.2 shall be

computed considering the appropriate ligament efficiency for the location of interest.

5.E.4.3 The effective elastic constants of the perforated plate material are determined based on the hole

pattern and thickness of the plate. Either one of the following two options may be used in the analysis.

a) Option A – The effective elastic constants are provided below. Elastic constants are provided for the

effective elastic modulus and effective Poisson’s ratio. A value for the effective shear modulus, which is

required in the analysis method in this annex, is not provided. The effective shear modulus shall be

evaluated using Option B.

1) Triangular Hole Pattern – The effective elastic modulus and effective Poison’s ratio are provided in

Tables 5.E.1 and 5.E.2, respectively.

2) Square Hole Pattern – The effective elastic modulus and effective Poisson’s ratio are provided in

Tables 5.E.3 and 5.E.4, respectively. The effective elastic modulus and Poisson’s ratio represent

an equivalent isotropic value considering the values of the pitch and diagonal properties.

3) Range of Applicability – The range of applicability in terms of the effective tube pitch is

0.1 1.0

≤≤. The effective elastic constants

E and

can be used for in-plane loading and

bending loading of all values of

hp.

4) The value of the in-plane shear modulus is given by Equation (5.E.1). The value of the out-of-plane

shear modulus

G shall be computed using Option B.

()

(5.E.1)

2010 SECTION VIII, DIVISION 2

5-98

b) Option B – The effective elastic constants for plane stress and generalized plane strain are provided

below.

1) Triangular Hole Pattern – The effective elastic modulus and effective Poison’s ratio are provided in

Table 5.E.5

2) Square Hole Pattern – The effective elastic modulus and effective Poisson’s ratio for the pitch and

diagonal directions are provided in Tables 5.E.6 and 5.E.7, respectively.

3) Effects Of Poisson’s Ratio – The effective material constants in Tables 5.E.5, 5.E.6, and 5.E.7 are

based on a Poisson’s ratio of

0.3

= . The material constants can be determined for other values

of Poisson’s ratio using the following procedure.

i) For a given value of

, determine

E and

using the equations in Tables 5.E.5, 5.E.6, and

5.E.7, as applicable. These values correspond to

0.3

ii) Determine

F using the following equation:

= (5.E.2)

iii) Determine

F using the following equation:

0.3FF

=− (5.E.3)

iv) The value of

for any value of the Poisson’s ratio,

, is:

() FF

νν

(5.E.4)

v) With the value of

()

determined above, the effective elastic modulus and shear modulus

can be determined for any value of the Poisson’s ratio by using the equations in Tables 5.E.5,

5.E.6, and 5.E.7, as applicable.

4) Range of Applicability – The range of applicability in terms of the effective tube pitch is

0.1 1.0

≤≤. The range of applicability in terms of hp is:

i) The effective elastic constants

E and

can be used for in-plane loading and bending

loading when

2.0hp≥ .

ii) The effective elastic constants

E and

can be used for in-plane loading when 2.0hp

The effective constants in Option A can be used for bending loading when

2.0hp< .

iii) The effective elastic constants

G ,

G , and

G can be used for in-plane loading and

bending loading for all values of

hp.

iv) The effective elastic constants for plane stress shall be used when

2hp< , and the effective

elastic constants for generalized plane strain shall be used when

2hp≥ .

c) Option C – The effective elastic constants for the geometry being evaluated can be derived by stress

analysis. In this case, the tube layout geometry is modeled and loads are applied to introduce normal

and shear stresses. The effective elastic constants can be derived from the stress and strain results

from the stress analysis.

标准分享网 www.bzfxw.com 免费下载