ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

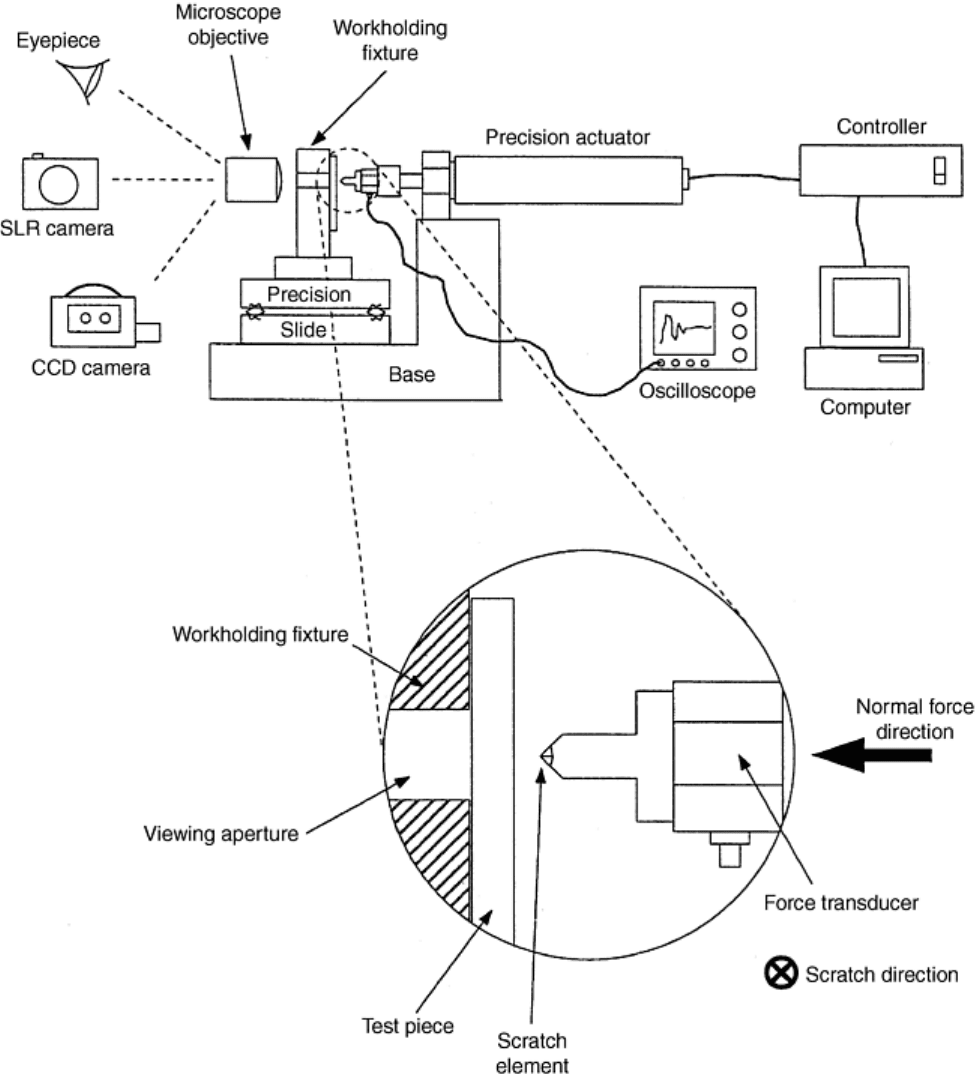
Fig. 4 Purdue scratch apparatus for in situ viewing of scratch formation

Reference cited in this section

4. S. Jacobsson, M. Olsson, P. Hedenqvist, and O. Vingsbo, Scratch Testing, Friction, Lubrication, and

Wear Technology, Vol 18, ASM Handbook, ASM International, 1992, p 430–437

Scratch Testing

Vispi Homi Bulsara, Cummins Engine Company;Srinivasan Chandrasekar and Thomas N. Farris, Purdue University

Test Parameters

When a scratch test is used to determine the scratch hardness of a material, the test has to be performed in a

controlled or standard configuration. The important parameters of the test are highlighted and briefly described.

Indenter Material. For most tests, a diamond indenter is used to minimize the wear on the indenter and to

reduce the influence of wear on the mechanism of scratching. Other hard materials, such as sapphire and

tungsten carbide, may also be used as indenters provided they are much harder than the material being

scratched. It should be noted that for wear tests—since wear properties of a pair of materials, that is, a material

system, are usually studied—the scratch element is made of one material, not necessarily a hard material such

as diamond, while the sample may be made of another material.

Indenter Shape. The shape of the indenter is usually spherical (or ball), conical with a sharp tip, a four-faced

pyramid (Vickers, Knoop), or a triangular (Berkovich) pyramid. The radius of the indenter tip for a sharp

indenter should not be larger than a prescribed amount, and it should be at least an order of magnitude less than

the depth of the scratch. Typical indenter radius for a Vickers indenter is <2 μm. It is important that the indenter

tip shape is carefully characterized before testing. Conical or pyramid indenters are commonly used in scratch

tests, since they can produce a plastic scratch even in brittle materials.

Orientation of the Indenter Relative to the Scratch Direction. In the case of a nonaxisymmetric indenter, such as

a pyramid indenter, the diagonal of the indenter is aligned parallel to the scratch direction to reduce cracking in

brittle materials and formation of a chip in ductile materials.

Indenter Angle of Attack. This is the angle made by the leading face of the indenter with the sample surface.

Usually, the axis of the indenter is aligned perpendicular to the sample surface with the sharp tip (apex) digging

in to the sample. However, in some scratch tests this is not necessarily the case. For example, in the Birnbaum

scratch hardness test, the leading edge of the cubic indenter (formed by the corner of a cube) is at 35° to the

sample surface, hence orienting the main diagonal at 80° to the sample surface.

Sample Preparation. The sample surface is usually polished to a micron or submicron arithmetic average

roughness (R

) to minimize the influence of roughness on the test results. The R

of the surface should be an

order of magnitude less than the depth of the scratch. By a suitable series of polishing steps, it is feasible to

achieve R

values as small as 10 nm fairly easily.

Scratch Velocity. The relative velocity between the indenter and the work surface is held constant during the

test. In older scratch devices, the velocity was controlled by weights, attached to the slide (on which the work

material or indenter is installed), which was passed over a pulley; by varying the weights it was possible to

obtain different scratch velocities. In devices used at the time of publication, the slide is driven by a motor with

precise velocity and position control.

Scratch Length or Duration. In order to avoid end effects associated with sample edges and obtain steady-state

data, the length of the scratch should be at least 20 times greater than the depth or width of the scratch

(whichever is larger).

Scratch Load or Depth. Either scratch load or the depth of indenter penetration can be set at a fixed amount

throughout the test. It should be noted that for testing the strength of coatings, the depth of the scratch or the

normal load on the indenter is increased at a fixed rate as the indenter is traversed across the sample. The

scratch depth is controlled by aligning the scratch direction parallel to the surface of the test material. The

scratch load is held constant by the use of deadweights to apply the load. Alternatively, load cells can be used to

monitor the scratch load and a feedback mechanism used to move the indenter into or away from the sample

surface to maintain constant load.

Number of Passes. This is the number of times the indenter passes over the same scratch track. In most scratch

tests, only a single scratch track is made in the sample. Wear tests involve several passes of the scratch element

over the same scratch track.

Determination of Scratch Width or Depth. If the scratch width and depth are determined visually using an

optical microscope, the magnification, lighting, and grid/scale used should be standardized to enable

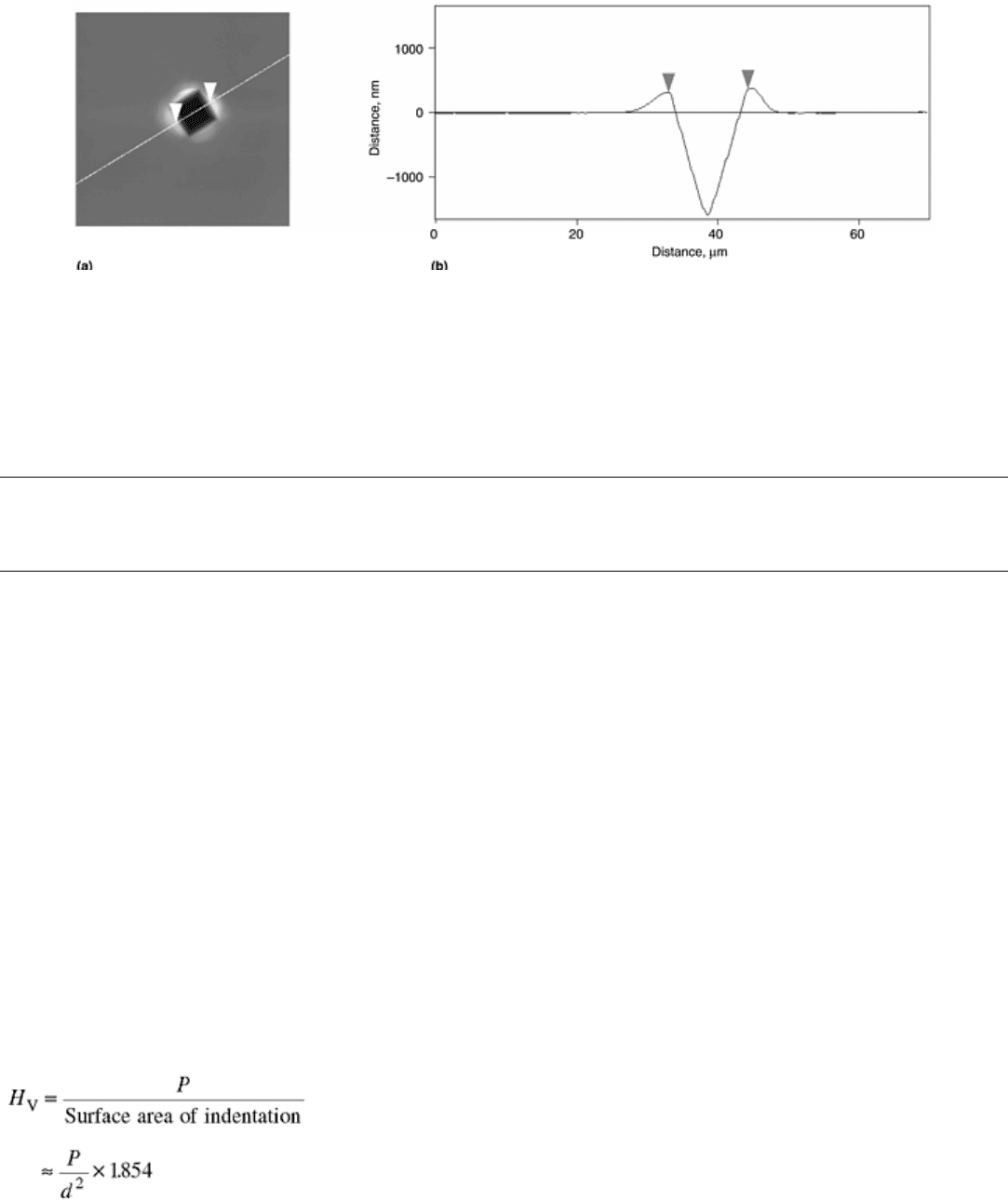
reproducibility of results. If the scratch cross-section profile is determined by contact (stylus)-based methods,

parameters such as filter type, cutoff length, stylus travel velocity, and stylus tip radius have to be standardized.

In the recent past, techniques such as scanning probe microscopy (atomic force microscopy and scanning

tunneling microscopy), confocal microscopy, and light-interference-based profilometry have improved the

accuracy and resolution of measurement of scratch width and depth. The techniques also provide information

about the three-dimensional geometry of the scratch including material pileup, elastic recovery, and so forth

(Fig. 5).

Fig. 5 Cross section of a Vickers indentation in iron along a line joining the midpoints of opposite edges

of the indentation (load ≈ 40 g). (a) Plan view of the indent. (b) Atomic force microscopy line profile

along the section line marked in (a). Section details: surface distance, 29.7 μm; horizontal distance, 28.8

μm; vertical distance, 46.8 nm; angle, 0.093°

Scratch Testing

Vispi Homi Bulsara, Cummins Engine Company;Srinivasan Chandrasekar and Thomas N. Farris, Purdue University

Application and Interpretation of Results

Before discussing the application of the scratch test to determine different parameters pertaining to the

deformation and fracture of solids, it is instructive to briefly review the measurement of indentation hardness

(which is discussed in more detail in the Section “Hardness Testing” in this Volume).

Overview of Indentation Hardness. The indentation hardness test has found widespread application in analyzing

the mechanical properties of materials. The most common method of estimating indentation hardness of a solid

is by slowly loading an indenter, sharp or blunt, into the surface and estimating the contact pressure applied by

the indenter in producing a well-developed plastic zone. In practice, the contact dimensions of the indentation,

that is, the contact circle diameter for a spherical indenter and the diagonal lengths for pyramidal indenters, are

measured after the indenter is unloaded from the surface. The hardness is obtained most commonly as the load

(P) divided by the surface area of the indentation. A better hardness value, referred to as true hardness, is

obtained by dividing the load by the projected area of the indentation. This value can be directly identified with

the mean pressure, p

, applied by the indenter, if it is assumed, as is commonly done, that the projected area of

the indentation is negligibly changed by the elastic recovery taking place during unloading of the indenter.

Applying these definitions to the case of quasistatic loading of a solid by a Vickers indenter, which produces a

pyramid indentation, the Vickers indentation hardness (H

) is obtained as:

(Eq 3)

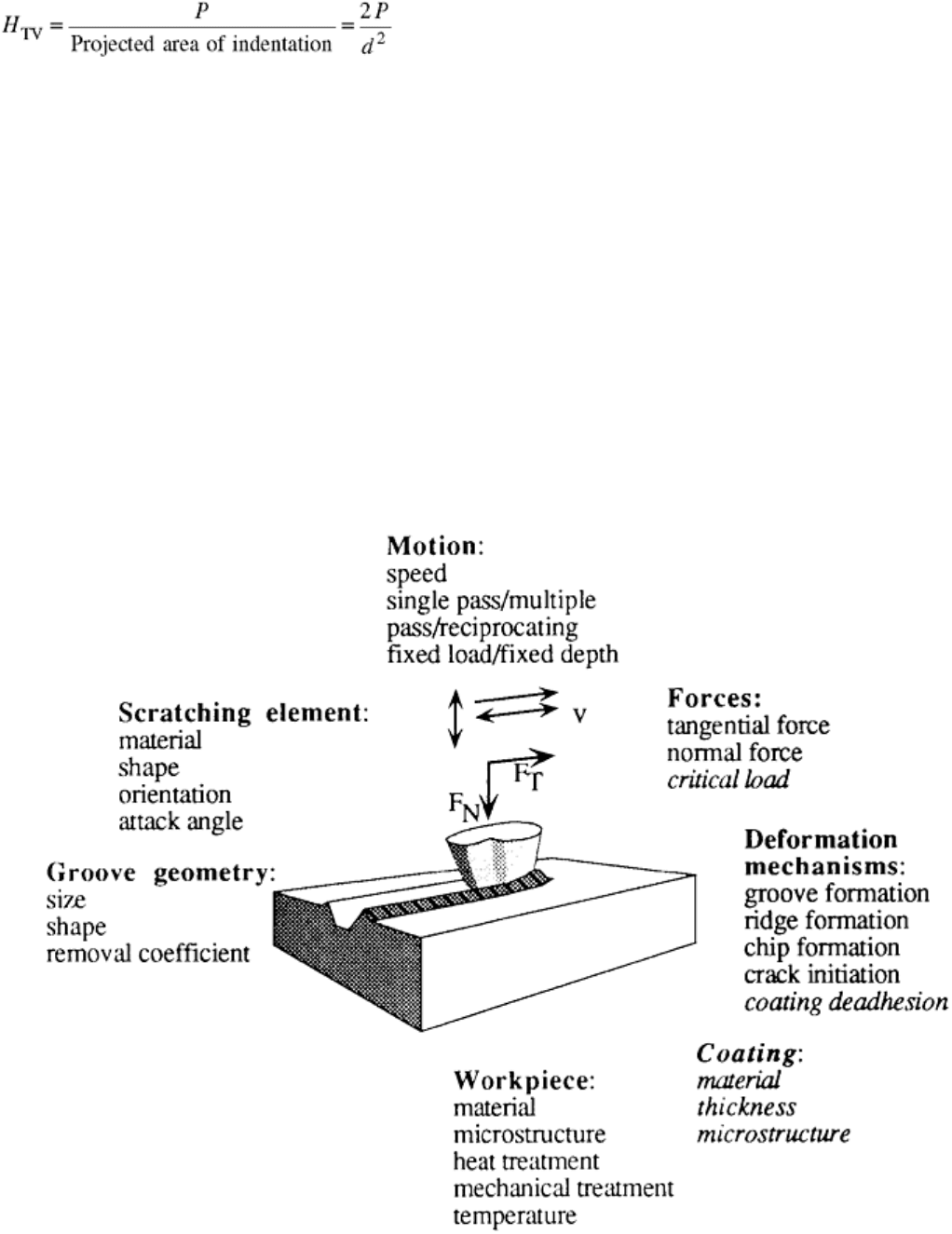
Here d is the diagonal length of the indentation and P is the maximum load applied by the indenter. A true

value for the Vickers hardness, namely the true Vickers hardness (H

), is estimated as:

(Eq 4)

Note that H

= 0.927 H

. For most materials, it is commonly assumed that H

≈ 3σ

where σ

is the yield

strength of the material.

It is most often the case that during indentation part of the displaced material is piled up in the form of a ridge

surrounding the indentation. This is well illustrated by the atomic force microscopy image and associated line

trace of a Vickers indentation shown in Fig. 5. When obtaining the contact area for Eq 3 and 4, it is assumed

that the pileup of the material produced during indentation does not support any load. In practice, the piled-up

material does, in fact, support a load.

Scratch Hardness Estimation. Now consider what happens to a Vickers indenter if it is moved along the sample

surface, after a load, P, has been applied. This corresponds to a scratch test. For the purpose of discussion it

shall be assumed, without loss of generality, that the pyramid indenter is being moved along the direction of

one of the indentation diagonals. As the indenter is quasi-statically loaded and then slid against the surface, the

indenter first sinks further into the surface due to loss of load-carrying capacity of the two rear faces. As sliding

proceeds, the indenter will “climb up,” pushing a ridge of deforming material ahead of it. A steady state is soon

reached in which the normal force, P, the tangential force, F, and the extent of plastic deformation as

characterized by the width of the scratch track become constant. A schematic of a scratch track and an optical

micrograph of the plan views of a track made by a Vickers indenter are shown in Fig. 6 and 7, respectively.

Figure 8 is a schematic of the relevant load-bearing areas associated with the normal and tangential force,

respectively, which enter into the calculation of scratch hardness.

Fig. 6 Parameters encountered in scratch testing. F

, tangential friction force; F

, normal load; v,

scratching speed

Fig. 7 The load dependence of fracture and deformation about scratches made by a Vickers indenter in

soda-lime glass. These photographs were taken in tests conducted in the Purdue scratch apparatus. (a)

Scratch appears plastic until end of traverse. Load, 120 g. (b) Lateral and median cracks pop up around

the scratch track, shown in (a), when the indenter is unloaded. (c) Lateral and median cracks after

unloading. Load, 90 g. A, extent of median crack; B, extent of lateral crack. (d), (e), and (f), different

parts of the same scratch track showing ductile chip formation at low loads. A, curly chip; B, spiral chip;

C, chips attached to groove surface

Fig. 8 Effect on load-bearing area, A

, of scratching with a conical tool. (a) Pure cutting (no ridge

formation). (b) A more realistic situation of ridge formation (that is, mixed microplowing and

microcutting). w, groove width; b, groove height

The scratch hardness may also be defined with reference to Fig. 8. By analogy with quasi-static indentation, the

scratch hardness H

is defined as (Ref 6):

(Eq 5)

The projected load-bearing area, A

, is estimated from measurements of the scratch track width, w. In practice,

if w is measured with an optical microscope, some part of the piled-up region along the lateral edges of the

track will be included in the measurement. For a Vickers indenter, A

is obtained as:

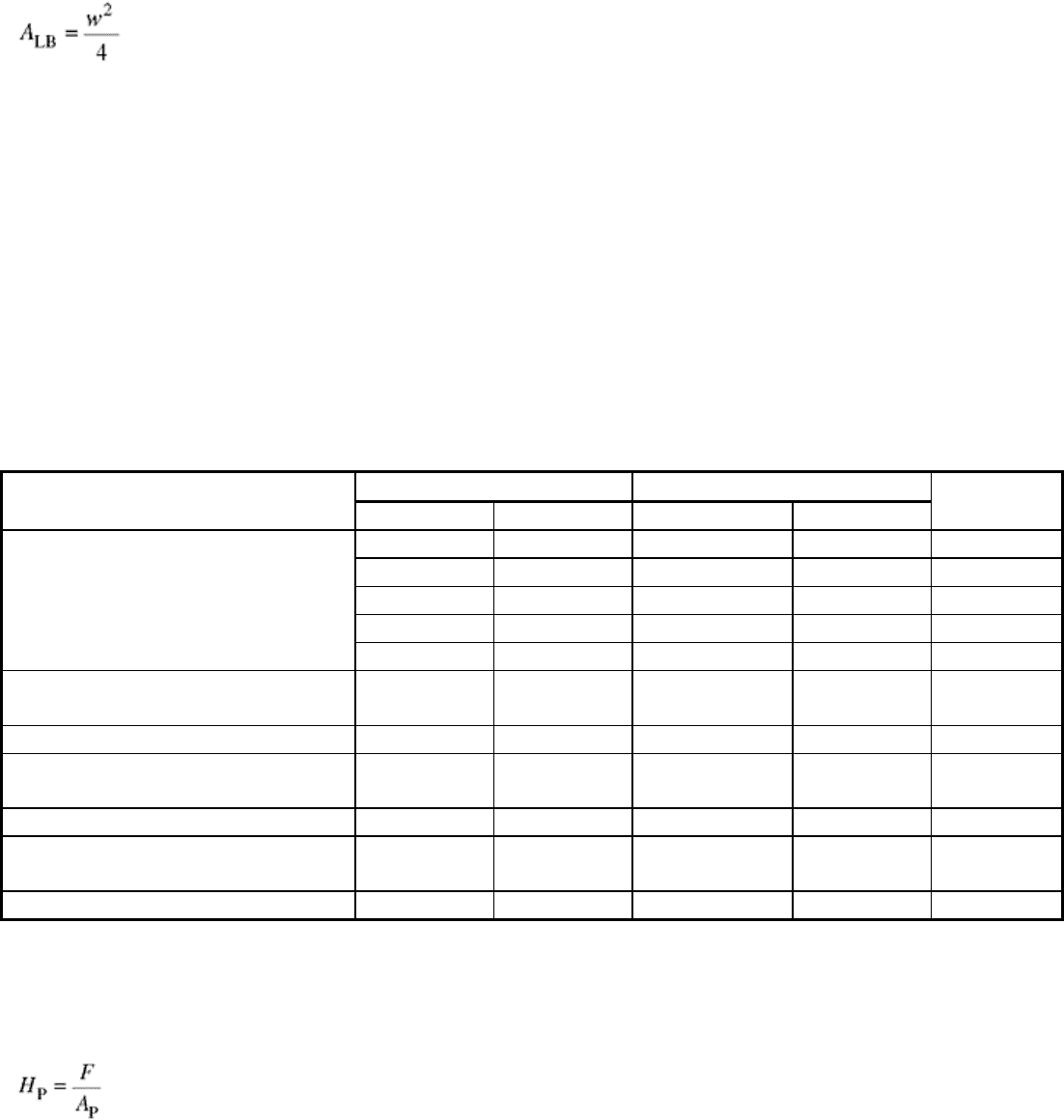
(Eq 6)

Similar relations can be obtained easily for other indenter geometries. Note that A

for a Vickers indenter

calculated using Eq 6 is independent of whether the indenter is moved edge first or face first.

It is reasonable to expect that the scratch hardness, H

, is equal to the associated indentation hardness (Vickers,

Knoop, Brinell), H, since both parameters are associated with the plastic response of a material. However,

experimental results indicate otherwise. Table 1 is a comparison of indentation hardness (H) and scratch

hardness, H

, for a selection of materials. It is seen that the ratio H

/H is not only different from a value of one,

but also varies widely, depending on material type and properties. In order to understand these variations, it is

necessary to analyze a detailed model of the plastic scratching process (Ref 6), but this is beyond the scope of

this article. Suffice to say that H

may be used in an analogous way to indentation hardness, but with

considerable caution. From a measurement point of view, the measurement of scratch width, including the

pileup region, is much easier and can be more accurately carried out than indentation diagonal measurement.

For example, profilometry of the scratch track provides an accurate measurements of w.

Table 1 Comparison of indentation hardness H and scratch hardness H

for a range of materials

H H

Material

MPa ksi MPa ksi

2,800 405 3,300 480

1.16

3,340 485 4,200 610

1.26

4,330 630 5,650 820

1.31

7,530 1,090 8,800 1,275

1.17

0.9% carbon steel

9,420 1,365 10,700 1,550

1.14

Aluminum

Annealed

216 31 196 28

0.91

Worked 422 61 245 35

0.58

Copper

Annealed

530 76 903 130

1.70

Worked 1,079 155 853 125

0.79

0.2% carbon steel

Annealed

1,265 185 1,295 190

1.02

Worked 2,354 340 2,247 325 0.95

Source: Ref 6

Plowing Hardness. When performing a scratch test, the tangential force (F) on the indenter is also measured.

This leads to the definition of another hardness parameter that is based on the groove cross-sectional area, A

and the tangential force (see Fig. 8). This hardness parameter is usually referred to as plowing hardness (H

)

and is defined as (Ref 6):

(Eq 7)

For a Vickers indenter, or more generally for scratching with a wedge indenter of wedge apex angle 2α,

= b

tan α

(Eq 8)

where b is the depth of the scratch groove measured either from the original surface or from the peak of the

piled-up region. The corresponding area A

for this wedge indenter is b

tan

α. It must be noted that b cannot

be estimated from track width, w, and the indenter angle 2α, because of elastic recovery of the scratch.

Consequently, b has to be obtained from a measurement. The quantity H

can be interpreted in more than one

way. For example, it can be thought of as the energy expended in displacing a unit volume of material. It is also

related to the minimum load required for a chip to be formed during scratching. However, the demarcation

between the deformation regimes in which chip formation is the preferred mode rather than indentation is

primarily dependent on the attack angle of the indenter, and to a lesser extent on indenter tip radius.

Specific Energy of Abrasive Machining. The scratch test, with a pyramid indenter or an abrasive particle, can

be used to estimate the specific energy (u) in abrasive machining, that is, the energy required to remove unit

volume of material by chip formation. The specific energy can be obtained as:

(Eq 9)

where F is the tangential or cutting force on the particle, b is the depth of material removed, and w is the width

of the scratch track.

The specific energy is an important parameter used to evaluate the efficiency of machining processes. It can

also be a useful parameter in studying the cutting action of abrasive grits of different type, shape, and

composition. The challenge in using this approach is that high-frequency dynamometers capable of measuring

the force on a single indenter or particle that is imposed over a duration of a few tens of microseconds are not

currently available. There are other approaches to estimating the energy consumed during cutting, but these are

not sufficiently accurate, nor do they have high resolution.

Efficiency of Material Removal. The scratch test can be used to evaluate the efficiency of material removal by

calculating a parameter that compares the amount of material removed by chip formation with the volume

displaced by indentation. This parameter, sometimes called the removal coefficient, η, is defined as:

(Eq 10)

The challenge in estimating this parameter is quantifying the amount of material that is piled up (see earlier

discussion).

Stress analysis of scratch testing is used to determine whether information more detailed than scratch hardness

is available within the test. Analysis of the stress field induced by scratch testing is difficult due to the

complicated geometry imposed by the contact problem and the inelastic behavior of the material in the presence

of concentrated stresses. Stress analysis of scratch testing can be classified broadly into indentation of ductile or

brittle materials by spherical or pyramidal indenters. The elastic stresses associated with a sliding spherical

indenter are well characterized, for example, in Ref 8. However, detailed elastic stress fields for pyramid

indenters are not available due to the singular nature of the stresses. These singularities require special care

when using finite elements to resolve elastic-plastic stress fields for normal indentation (Ref 9). An accurate

finite element solution for scratching using pyramid indenters is not available.

For spherical indenters, the finite-element method is capable of resolving the stresses associated with scratch

testing of ductile materials (Ref 10). However, an assumed constitutive behavior that is capable of accurately

predicting the ratcheting strain for repeated sliding of a range of materials eludes researchers (Ref 11). These

elastic-plastic calculations yield much information that is difficult to present in a compact form that can be used

to interpret experimental results over a range of loads. However, an approximate solution for ductile materials

subjected to normal indentation based on the “expanding cavity” are available (Ref 8). This solution relies on

an observation that strain fields are spherically symmetric. It provides a convenient classification of spherical

indentations into elastic, elastic-plastic, and fully plastic regimes. This model has not been applied to

scratching.

References cited in this section

6. J.A. Williams, Analytical Models of Scratch Hardness, Tribol. Int., Vol 29 (No. 8), 1996, p 675–694

8. K.L. Johnson, Contact Mechanics, Cambridge, 1985

9. Y. Murakami and K. Matsuda, Analysis of Vickers Hardness by the Finite Element Method, J. Appl.

Mech., Vol 61 (No. 4), 1994, p 822–828

10. S.M. Kulkarni, G.T. Hahn, C.A. Rubin, and V. Bhargava, Elasto-plastic Finite Element Analysis of

Three-Dimensional Pure Rolling Contact above the Shakedown Limit, J. Appl. Mech., Vol 58 (No. 2),

1991, p 347–353

11. C. Sakae and L.M. Keer, Application of Direct Method for a Nonlinear-Kinematic-Hardening Material

under Rolling/Sliding Line Contact: Constant Ratchetting Rate, J. Mech. Phys. Solids, Vol 45 (No. 9),

1997, p 1577–1594

Scratch Testing

Vispi Homi Bulsara, Cummins Engine Company;Srinivasan Chandrasekar and Thomas N. Farris, Purdue University

Sliding Indentation Fracture of Brittle Materials

The Blister Field. Recent interest in fracture induced by sliding indentation of brittle materials warrants special

attention. When a sharp indenter is quasi-statically applied onto a surface of a brittle solid, the classical theory

relating the hardness to the yield stress of metals (Ref 1) no longer applies since yielding no longer occurs at a

constant maximum shear stress or at a constant volume (Ref 12). A large body of experimental observations

have shown that in brittle materials the volume of material displaced by the penetration of the indenter is

accommodated by compaction or shear deformation, or both, and this may occur either uniformly or irregularly.

In silicate glasses, which have a relatively open structure, the displaced material is most readily accommodated

by compaction within a zone underneath the indenter. However, in soda-lime glasses and in most ceramics

shear deformation dominates, with some compaction also taking place underneath the indenter. The

experimental model used by Yoffe (Ref 13) to describe the deformation underneath a sharp conical indenter in

soda-lime glass is based on the work of Peter (Ref 14), among others, who showed that the mean contact

pressure under a sharp indenter remains constant and relatively independent of the indenter geometry. This

model assumes that as a conical indenter is applied to the solid surface, yielding initially occurs in a

hemispherical bowl under the indenter and continues until the yielded zone attains its stable preferred state for

that pressure. As the indenter is loaded further, no additional flow occurs within this bowl, but fresh yielding

takes place in an adjoining thin hemispherical shell. This process continues, and “it is as if a set of nested

hemispherical bowls separated by plastic filler were forced down in turn, one within the other” (Ref 13). The

yielding process occurs through a combination of shear deformation and compaction within the yielded zone.

Part of the material displaced by the indenter is accommodated by compaction within the yielded zone, while

the remaining material is pushed into the surroundings. At the end of the indentation process, the elastic half-

space is left with an overlarge hemispheroid fixed in a hemispherical cavity on its surface. This misfit leads to a

residual stress in the region outside of the cavity. Consequently, as the material reacts to this residual stress,

cracking may occur within the solid.

The “blister” field proposed by Yoffe (Ref 13) was for describing the development of cracks below a conical

indenter acting on a brittle solid. The stress distribution in the surrounding elastic zone was obtained as the

superposition of two stress fields—the Boussinesq field for the point force, which idealized the indentation

pressure distribution, and a doublet force system, which idealized the localized inelastic deformation. The

doublet force system for the blister field consisted of superposition of a point center of expansion in an infinite

elastic solid with an additional doublet to satisfy the free surface normal stress boundary condition. Such a

doublet force system leads to a volume increase of the inelastic deformation zone that must be taken up by

compaction or elastic deformation of the remainder of the solid. The volume increase is a measure of the

“strength” of the blister field. The strength of the blister field varies with the applied force; this variation is

characterized by a material property that has thus far defied a precise estimation. Qualitatively, Yoffe's model

has predicted the origin and growth of radial, median, and lateral crack systems quite well. In particular it is

consistent with the observation that for a certain range of loads, the lateral crack forms and grows during

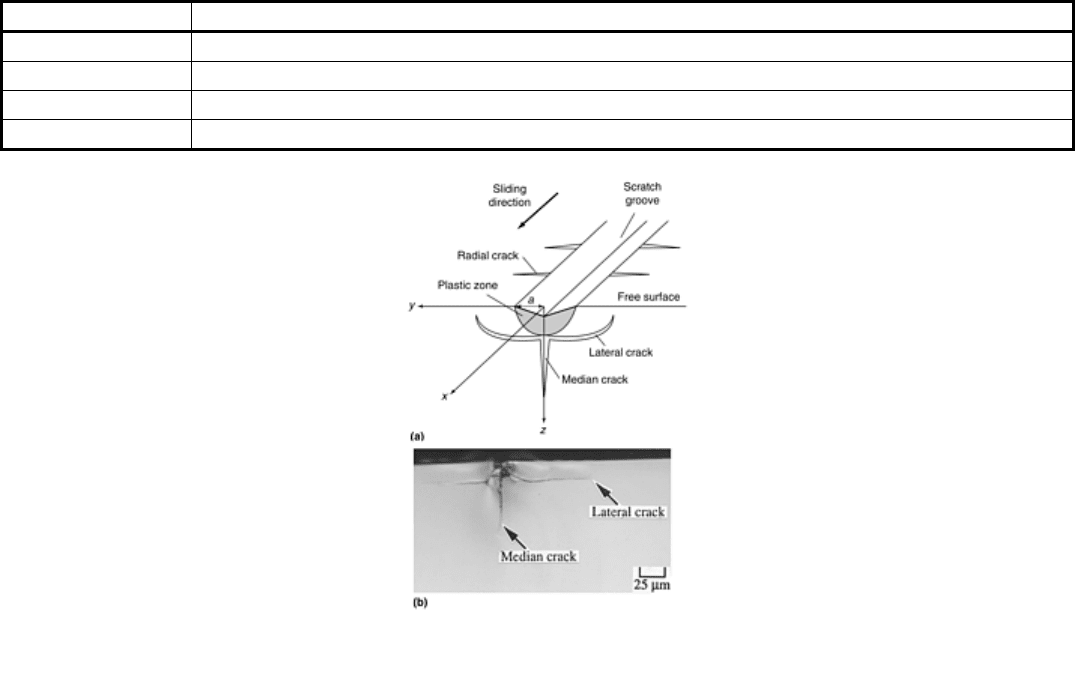
unloading. Its only disadvantage is from a quantitative point of view, as a procedure for determining the

strength of the blister field for various indenter geometries is not yet available.

Models to describe the sliding indentation fracture process in ceramics have not yet evolved to a stage where

the inelasticity under the indenter is accounted for completely (Ref 15, 16, 17). This is in large part due to the

difficulty introduced by a lack of information concerning the constitutive behavior of ceramics in large

hydrostatic compressive stress fields such as that existing underneath a microindentation. It seems that a

reasonable first step for modeling the sliding indentation stress fields would be to extend Yoffe's work on static

indentation to the sliding situation (Ref 18). This extension includes the load-history effects of inelastic

deformation left behind by the sliding indenter and the elastic effects due to the frictional force.

Sliding Indentation Fracture Observations. The sliding indentation stress field (Ref 18) provides interpretation

of observations of the microcracking about scratches in brittle solids (Ref 15, 16, 19, 20). Figure 9(a) shows a

schematic view of the crack patterns that have emerged from the studies, most of which have been carried out at

light loads in soda-lime glass, silicon, polycrystalline alumina, and nickel-zinc ferrite. The typically observed

crack patterns are median, lateral, and chevron (radial) cracks. The load regimes at which the various cracks

occur in soda-lime glass are summarized in Table 2, which is obtained based on observations of the fractured

specimen.

Table 2 Classification of fracture patterns in soda-lime glass under a sliding Vickers indenter

Normal load (N)

Fracture pattern

~0–0.05

No crack

~0.05–0.8

Median cracking

~0.8–3

Median and lateral cracking with lateral crack growth to the surface at higher loads

~3–6 Median cracking and crushed scratch track

Source: Ref 19

Fig. 9 (a) Cracks induced by sliding microindentation of brittle solids. (b) Photograph of cross section

In situ observations indicate that these cracks initiate at or close to the boundary between the inelastic

deformation zone and the surrounding elastic solid. The subsequent growth of these cracks occurs in the elastic

region. Bulsara (Ref 20) observes that for most loads at which median and lateral cracks occur, the cracks

propagate such that the crack front moves with the load. However, near loads of about 1 N applied with a

Vickers indenter in soda-lime glass, the lateral crack does not appear until the indenter is lifted from the

surface. Once the load is removed, the lateral crack forms beneath the end of the scratch and propagates rapidly

along the entire length of the scratch and until the beginning of the scratch track, where it stops. Fracture and

deformation patterns about scratches in soda-lime glass, which is often used as a model brittle material, as

shown in Fig. 7, which also shows ductile chips formed by scratching in glass.

The assumption that these cracks are initiated and propagated by tensile stresses that occur in the elastic

material immediately adjoining the inelastic zone allows for predictions of crack formation and growth through

a consideration of the stress fields. It has been shown that the present analytical model provides reasonably

good descriptions of the crack patterns observed around sliding indentations in brittle materials. In particular,

the analysis accounts for the occurrence of lateral cracking under sliding indenters above an experimentally

observed threshold load (Ref 18).

The sliding blister field does not reveal any information about details of deformation in the inelastic zone near

the indenter. Recently, investigators have been examining this issue using nanoscratch testing. However, the

sliding blister field is a simple analytical tool that can be used to explain many interesting aspects of failure

mechanisms in glass that occur near sliding microindentations.

Sliding Indentation Modeling of Polishing. A common method for making surfaces smooth is by rubbing them

against a block with an abrasive slurry interspersed between them. This process is called polishing or,

sometimes, lapping. The block is typically made of a metal, for example, cast iron or tin, or it consists of a soft,

flexible material such as cloth, nylon, or leather attached to the surface of a metal block. The polishing slurry is

composed of hard, abrasive particles (e.g., diamond, silicon carbide, alumina) suspended in a fluid medium

such as deionized water, glycol, or viscous oil. A force is applied to the work surface by the polishing block;

this force typically corresponds to a polishing pressure of 7 to 14 kPa (1–2 psi), where polishing pressure is the

polishing force divided by the work surface area. The relative sliding velocity between the block and the work

surface is usually less than 0.5 m/s and randomly oriented through the course of the process so as to produce a

smooth surface devoid of directional scratches. This velocity is one to two orders of magnitude less than the

relative velocity between an abrasive wheel and workpiece in grinding. An early, important application of

polishing was lens making, and indeed it was for this purpose that the process was studied by Newton,

Herschel, and Rayleigh (Ref 21). Since then, polishing has become a critical process in many applications

ranging from the manufacture of precision mechanical components to electronic substrates and optical

windows.

While the applied polishing force is low and in itself insufficient even to cause considerable elastic deformation

of the work surface, this force is transmitted to the surface, not uniformly, but at the microscopic contacts

between the abrasive particles and the work surface (Ref 22, 23). At these contacts the pressure imposed by a

particle on the surface should be quite high, often comparable to the hardness of the work material.

Consequently, the mechanism of material removal in polishing, which varies from brittle fracture to plastic

microcutting, is not so much dictated by the applied polishing force as by the manner in which this force is

transmitted locally by the particles to the work surface. This is consistent with microscopic observations of

polished surfaces and polishing debris, which indicate that the abrasive particles act like single-point cutting

tools or indenters (Ref 22, 24). The force applied by an abrasive particle also plays a major role in determining

polishing temperatures (Ref 25) and the extent of plastically deformed layers and residual stresses on polished

surfaces (Ref 22, 26, 27). Because of the critical importance of these forces to the mechanics of polishing, it is

of interest to deduce the magnitude and distribution of these forces and their dependence on polishing

parameters.

A model has been developed to determine the number and size of abrasive particles involved in material

removal in polishing and the forces acting on these particles (Ref 28). This model assumes that each particle

acts as a sliding microindentation. The effect of particle size on these parameters has been simulated for a range

of particle sizes. It is shown that when polishing with abrasive powders having relatively broad size

distributions, only a very small percentage of the particles are involved in material removal. Further, these

particles comprise the larger particles occurring in the tail end of the particle size distribution. The average

force on a particle is found to be in the range of 5 to 200 mN under typical polishing conditions, which is of the

order of loads used in microindentation hardness testing. These predictions of the model are consistent with

observations pertaining to polished surfaces and the polishing process.

References cited in this section

1. D. Tabor, The Hardness of Metals, Oxford University Press, 1951