ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation
Подождите немного. Документ загружается.


Fatigue and Fracture Mechanics
Introduction
FATIGUE is the progressive, localized, and permanent structural damage that occurs when a material is
subjected to cyclic or fluctuating strains at nominal stresses that have maximum values less than (and often
much less than) the static yield strength of the material (Ref 1). This process of fatigue failure can be divided
into different stages, which, from the standpoint of metallurgical processes, can be divided into five stages (Ref
1):
1. Cyclic plastic deformation prior to fatigue crack initiation
2. Initiation of one or more microcracks
3. Propagation or coalescence of microcracks to form one or more microcracks
4. Propagation of one or more macrocracks
5. Final failure
This division is defined by the characterization of the underlying fatigue damage of a material. It also clearly
defines the requirement of plastic deformation for the onset of crack initiation. In general, three simultaneous
conditions are required for the occurrence of fatigue damage: cyclic stress, tensile stress, and plastic strain. If
any one of these three conditions is not present, a fatigue crack will not initiate and propagate. The plastic strain
resulting from cyclic stress initiates the crack; and the tensile stress (which may be localized tensile stresses
caused by compressive loads) promotes crack propagation (Ref 1).
The stages of fatigue can also be defined in more general terms from the perspective of mechanical behavior of
crack growth. For example, another division of the fatigue process is defined as follows (Ref 2):
• Nucleation (initiation of fatigue cracks)
• Structurally dependent crack growth rates (often called the “short crack” or “small crack” phase)
• Crack growth rates that can be characterized by either linear elastic fracture mechanics, elastic-plastic
fracture mechanics, or fully plastic fracture mechanics
• Final instability
This definition of the stages in the fatigue process is roughly equivalent to the first, except that crack
propagation is expressed in terms of crack growth rates, and nucleation is meant to include all processes leading
up to crack initiation.
In general, the fatigue process consists of a crack initiation and a crack propagation phase. There is, however,
no general agreement when (or at what crack size) the crack initiation process ends, and when the crack growth
process begins (Ref 3). Nonetheless, the separation of the fatigue process into initiation and propagation phases
has been an important and useful advance in engineering.
Another important engineering advance is the transfer of the multistage fatigue process from the field to the
laboratory. In order to study, explain, and qualify component designs, or to conduct failure analyses, a key
engineering step is often the simulation of the problem in the laboratory. Any simulation is, of course, a
compromise of what is practical to quantify, but the study of the multistage fatigue process has been greatly
advanced by the combined methods of strain-control testing and the development fracture mechanics of fatigue
crack growth rates. This combined approach (Fig. 1) is a key advance that allows better understanding and
simulation of both crack nucleation in regions of localized strain and the subsequent crack growth mechanisms
outside the plastic zone. This integration of fatigue and fracture mechanics has had important implications in
many industrial applications for mechanical and materials engineering.
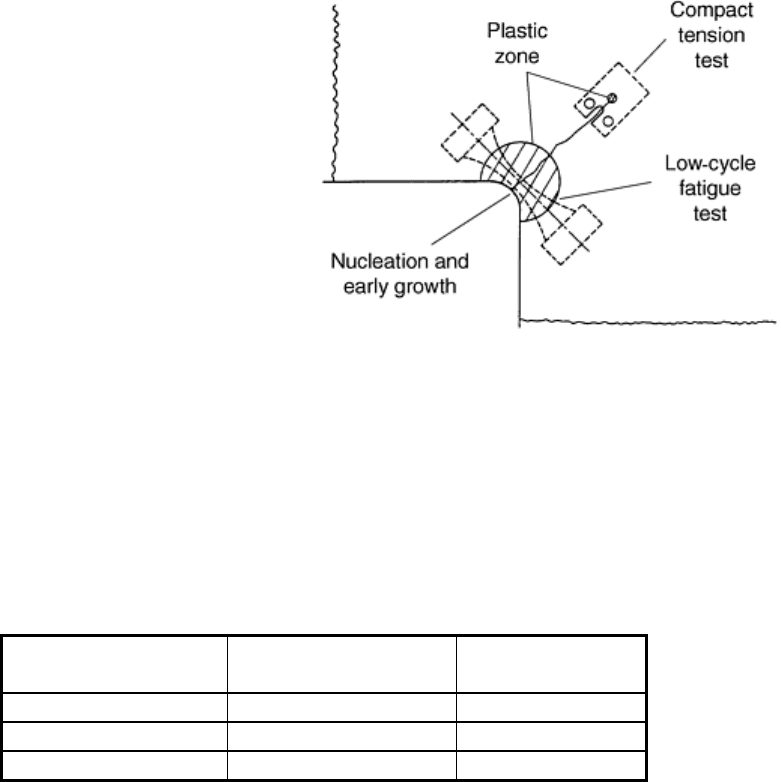
Fig. 1 Laboratory simulation of the multistage fatigue process. Source: Ref 2
This introductory article briefly reviews the three basic types of fatigue properties, which are:
• Stress-life (S-N)
• Strain life (ε-N)
• Fracture mechanic crack growth (da/dN-ΔK)
These three types of fatigue properties each play a role in engineering, and each property is used in the context
of an underlying fatigue design philosophy as follows:
Design philosophy Design methodology
Principal testing
data description
Safe-life, infinite-life
Stress-life S-N
Safe-life, finite-life Strain-life ε-N
Damage tolerant Fracture mechanics da/dN-ΔK
The S-N and ε-N techniques are usually appropriate for situations where a component or structure can be
considered a continuum (i.e., those meeting the “no cracks” assumption). In the event of a crack-like
discontinuity, the S-N or ε-N methods (except through residual life testing) offer little or quantitative basis for
assessment of fatigue life.
Another limitation of the S-N and ε-N methods is the inability of the controlling quantities to make sense of the
presence of a crack. A brief review of basic elasticity calculations shows that both stress and strain become
astronomical at a discontinuity such as a crack, far exceeding any recognized property levels that might offer
some sort of limitation. Even invoking plasticity still leaves inordinately large numbers or, conversely,
extremely low tolerable loads.
The solution to this situation is the characterization and quantification of the stress field at the crack tip in terms
of stress intensity in linear elastic fracture mechanics. It recognizes the singularity of stress at the tip and
provides a tractable controlling quantity and measurable material property. The use of the stress intensity as a
controlling quantity for crack extension under cyclic loading thus enhances the engineering analysis of the
fatigue process.
More detailed information on fatigue and fracture mechanics can be found in Fatigue and Fracture, Volume 19
of ASM Handbook.
References cited in this section
1. M.E. Fine and Y.-W. Chung, Fatigue Failure in Metals, Fatigue and Fracture, Volume 19, ASM
Handbook, ASM International, 1996, p 63–72
2. D.W. Hoeppner, Industrial Significance of Fatigue Problems, Fatigue and Fracture, Vol 19, ASM
Handbook, ASM International, 1996, p 3–4

3. E. Krempl, Design for Fatigue Resistance, Materials Selection and Design, Vol 20, ASM Handbook,
ASM International, 1997, p 516–532
Fatigue and Fracture Mechanics
Infinite-Life Criterion (S-N Curves) (Ref 4)
The safe-life, infinite-life philosophy is the oldest of the approaches to fatigue. Examples of attempts to
understand fatigue by means of properties, determinations, and representations that relate to this method include
August Wöhler's work on railroad axles in Germany in the mid-1800s. The design method is stress-life, and a
general property representation would be S-N (stress versus log number of cycles to failure). Failure in S-N
testing is typically defined by total separation of the sample.
General applicability of the stress-life method is restricted to circumstances where continuum, “no cracks”
assumptions can be applied. However, some design guidelines for weldments (which inherently contain
discontinuities) offer what amount to residual life and runout determinations for a variety of process and joint
types that generally follow the safe-life, infinite-life approach. The advantages of this method are simplicity and
ease of application, and it can offer some initial perspective on a given situation. It is best applied in or near the
elastic range, addressing constant-amplitude loading situations in what has been called the long-life (hence,
infinite-life) regime.
The stress-life approach seems best applied to components that look like the test samples and are approximately
the same size (this satisfies the similitude associated with the use of total separation as a failure criterion).
Much of the technology in application of this approach is based on ferrous metals, especially steels. Steels are
predominant as a structural material, but steels also display a fatigue limit or endurance limit at a high number
of cycles (typically >10
6
) under benign environmental conditions. The infinite-life asymptotic behavior of steel
fatigue life, thus, provides a useful and beneficial result of S-N testing. However, most other materials do not
exhibit this infinite life response. Instead, many materials display a continuously decreasing stress-life response,
even at a great number of cycles (10
6
-10
9
), which is more correctly described by a fatigue strength at a given
number of cycles.
Assessing Fatigue S-N Properties. Given the extensive history of the stress-life method, substantial property
data are available, but beware of the testing conditions employed in producing older data. The usefulness of
property data is a critical point due to the numerous variables that influence fatigue results. For example, if a
series of tests are conducted at a constant stress ratio (R = S
min
/S
max
), and the alternating stress amplitude (S
a
) is
used as the other independent dynamic variable, an S-N curve for that situation can be produced, and all
dynamic variables can be determined. However, if only one variable is given (e.g., S
a
or S
max
), there is
insufficient information to tell what the test conditions were and the data are virtually useless.
In many cases, insufficient information is available for the effective use of S-N data. Many necessary pieces of
data are simply missing. A partial list of important questions might be as follows:
• What were the coupon size and geometry?
• Was there a stress concentration?
• What was the temperature?
• Was an environment other than lab air employed?
• What was the specimen orientation in the original material?
• Does the line represent minimum, mean, or median response?
• How many samples were tested?
• What was the scatter?
• If the plot is based on constant-amplitude data, what were the frequency and waveform?
• Was testing performed using variable-amplitude loading? What was the spectrum?
• What was the failure criterion?
• If there were runouts, how were they handled and represented?
If the data found describe a thin sheet response, it is the wrong data. If the product form is correct, but the plot
represents testing done at R = 0.3 and fully reversed data are required, the plot may be helpful, but it is not what
is desired.
An example of what should be considered important as supporting facts can be found in ASTM E 468,
“Presentation of Constant Amplitude Fatigue Test Results for Metallic Materials.” It provides guidelines for
presenting information other than just final data.
S-N Data Presentation. Stress is the controlling quantity in this method. The most typical formats for the data
are plots of the log number of cycles to failure (sample separation) versus either stress amplitude (S
a
),
maximum stress (S
max
), or perhaps stress range (ΔS).
Mean stress influences are also very important, and each design approach must consider them. According to
Bannantine et al. (Ref 5), the archetypal mean (S
m
) versus amplitude (S
a
) presentation format for displaying
mean stress effects in the safe-life, infinite-life regime was originally proposed by Haigh. The Haigh diagram
can be a plot of real data, but it requires an enormous amount of information for substantiation. A slightly more
involved, but also more useful, means of showing the same information incorporates the Haigh diagram with
S
max
and S
min
axes to produce a constant-life diagram. Examples of these are provided subsequently.
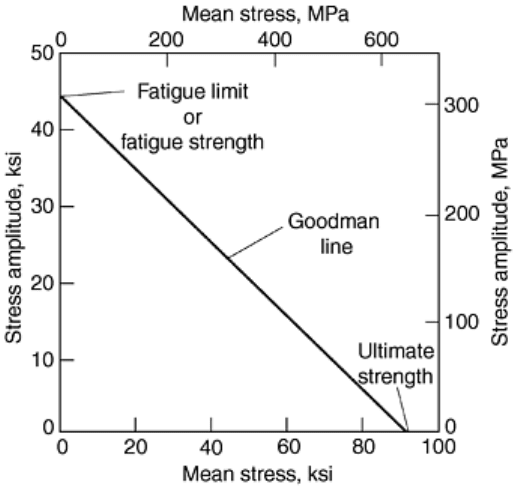
For general consideration of mean stress effects, various models of the mean-amplitude response have been
proposed. A commonly encountered representation is the Goodman line, although several other models are
possible (e.g., Gerber and Soderberg). The conventional plot associated with this problem is produced using the
Haigh diagram, with the Goodman line connecting the ultimate strength on S
m
, and the fatigue limit, corrected
fatigue limit, or fatigue strength on S
a
. This line then defines the boundary of combined mean-amplitude pairs
for anticipated safe-life response. The Goodman relation is linear and can be readily adapted to a variety of
manipulations.
In many cases Haigh or constant-life diagrams are simply constructs, using the Goodman representation as a
means of approximating actual response through the model of the behavior. For materials that do not have a
fatigue limit, or for finite-life estimates of materials that do, the fatigue strength at a given number of cycles can
be substituted for the intercept on the stress-amplitude axis. Examples of the Haigh and constant-life diagrams
are provided in Fig. 2 and 3. Figure 3 is of interest also because of its construction in terms of a percentage of
ultimate tensile strength for the strength ranges included.
Fig. 2 A synthetically generated Haigh diagram for an alloy steel (620 MPa, or 90 ksi, ultimate tensile
strength) based on typically employed approximations for the axes intercepts and using the Goodman
line to establish the acceptable envelope for safe-life, infinite-life combinations. The Goodman line
represents an unconnected 10
6
estimate at 50% failure (criterion: separation).
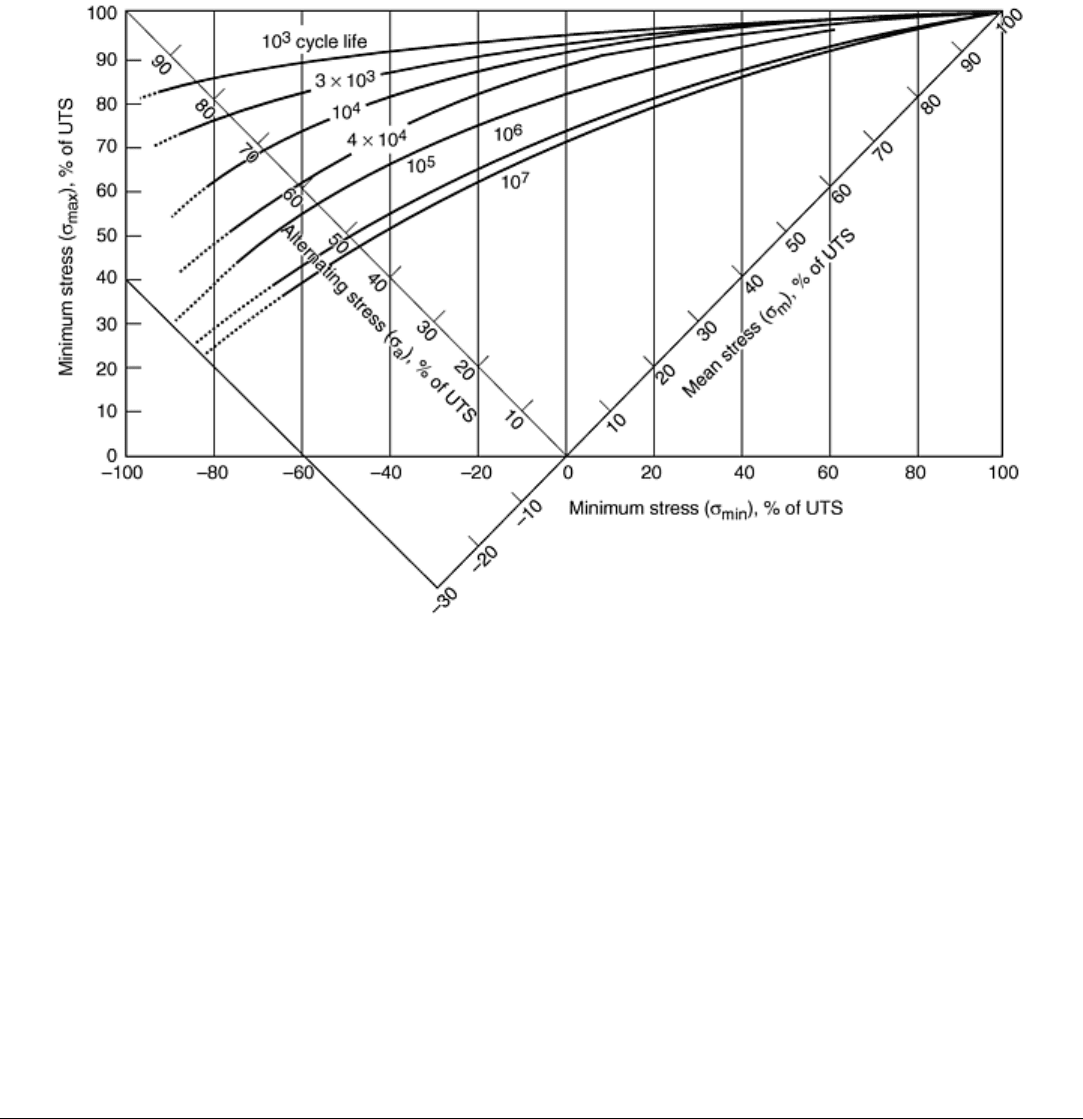
Fig. 3 A constant-life diagram for alloy steels that provides combined axes for more ready
interpretation. Note the presence of safe-life, finite-life lines on this plot. This diagram is for average test
data for axial loading of polished specimens of AISI 4340 steel (ultimate tensile strength, UTS, 860 to
1240 MPa, or 125 to 180 ksi) and is applicable to other steels (e.g., AISI 2330, 4130, 8630). Source: Ref 6
References cited in this section
4. D.W. Cameron and D.W. Hoeppner, Fatigue Properties in Engineering, Fatigue and Fracture, Vol 19,
ASM Handbook, ASM International, 1996, p 15–26
5. J.A. Bannantine, J.J. Comer, and J.L. Handrock, Fundamentals of Metal Fatigue Analysis, Prentice-
Hall, 1990
6. R.C. Juvinall, Engineering Considerations of Stress, Strain, and Strength, McGraw-Hill, 1967, p 274
Fatigue and Fracture Mechanics
Finite-Life Criterion (ε-N Curves) (Ref 4)
Strain life is the general approach employed for continuum response in the safe-life, finite-life regime. It is
primarily intended to address the low-cycle fatigue area (e.g., from approximately 10
2
to 10
6
cycles). The ε-N
method can also be used to characterize the “long-life” fatigue behavior of materials that do not show a fatigue
limit.
From a properties standpoint, the representations of strain-life data are similar to those for stress-life data.
However, because plastic strain is a required condition for fatigue, strain-controlled testing offers advantages in
the characterization of fatigue crack initiation (prior to subsequent crack growth and final failure). The S-N
method is based on just one failure criterion—the total separation of the test coupon. In contrast, any of the
following may be used as the failure criterion in strain-controlled fatigue testing (per ASTM E 606): separation,

modulus ratio, microcracking (initiation), or percentage of maximum load drop. This flexibility can provide
better characterization of fatigue behavior.
Testing for strain-life data is not as straightforward as the simple load-controlled (stress-controlled) S-N testing.
Monitoring and controlling using strain requires continuous extensometer capability. In addition, the
developments of the technique may make it necessary to determine certain other characteristics associated with
either monotonic or cyclic behavior. Further details on testing are given in the article “Fatigue, Creep Fatigue,
and Thermomechanical Fatigue Life Testing” in this Volume.
Reference cited in this section
4. D.W. Cameron and D.W. Hoeppner, Fatigue Properties in Engineering, Fatigue and Fracture, Vol 19,
ASM Handbook, ASM International, 1996, p 15–26
Fatigue and Fracture Mechanics
Fracture Mechanics Approach (Ref 7)
Fracture of structural and equipment components as a result of cyclic loading has long been a major design
problem and the subject of numerous investigations. Although a considerable amount of fatigue data are
available, the majority have been concerned with the nominal stress required to cause failure in a given number
of cycles—namely, S-N curves. Usually, such data are obtained by testing smooth specimens which, although
of some qualitative use for guiding material selection, are subject to limitations caused primarily by the failure
to adequately distinguish between fatigue-crack-initiation life and fatigue- crack-propagation life. The existence
of surface irregularities and cracklike imperfections reduces and may eliminate the crack-initiation portion of
the fatigue life of the component. Fracture-mechanics methodology offers considerable promise for improved
understanding of the initiation and propagation of fatigue cracks and problem resolution in designing to prevent
failures by fatigue.
Fatigue-Crack Initiation. Initiation of fatigue cracks in structural and equipment components occurs in regions
of stress concentrations, such as notches, as a result of stress fluctuation. The material element at the tip of a
notch in a cyclically loaded component is subjected to the maximum stress range, Δσ
max
. Consequently, this
material element is most susceptible to fatigue damage and is, in general, the origin of fatigue-crack initiation.
It can be shown that, for sharp notches, the maximum-stress range on this element can be related to the stress-
intensity-factor range, ΔK
I
, as follows (Ref 8):
(Eq 1)
where ρ is the notch-tip radius, Δσ is the range of applied nominal stress, and k
t
is the stress-concentration
factor.
Fatigue-crack-initiation behavior of various steels is presented in Fig. 4 (Ref 8) for specimens subjected to zero-
to-tension bending stress and containing a smooth notch that resulted in a stress-concentration factor of about
2.5. The data show that ΔK
I
/ , and, therefore, Δσ
max
is the primary parameter that governs fatigue-crack-
initiation behavior in regions of stress concentration for a given steel tested in a benign environment. The data
also indicate the existence of a fatigue-crack-initiation threshold, ΔK
I
/
th
, below which fatigue cracks would
not initiate at the roots of the tested notches. The value of this threshold is characteristic of the steel and
increases with increasing yield or tensile strength of the steel. The data show that the fatigue-crack-initiation
life of a component subjected to a given nominal-stress range increases with increasing strength. However, this
difference in fatigue-crack-initiation life among various steels decreases with increasing stress-concentration
factor (Ref 8).
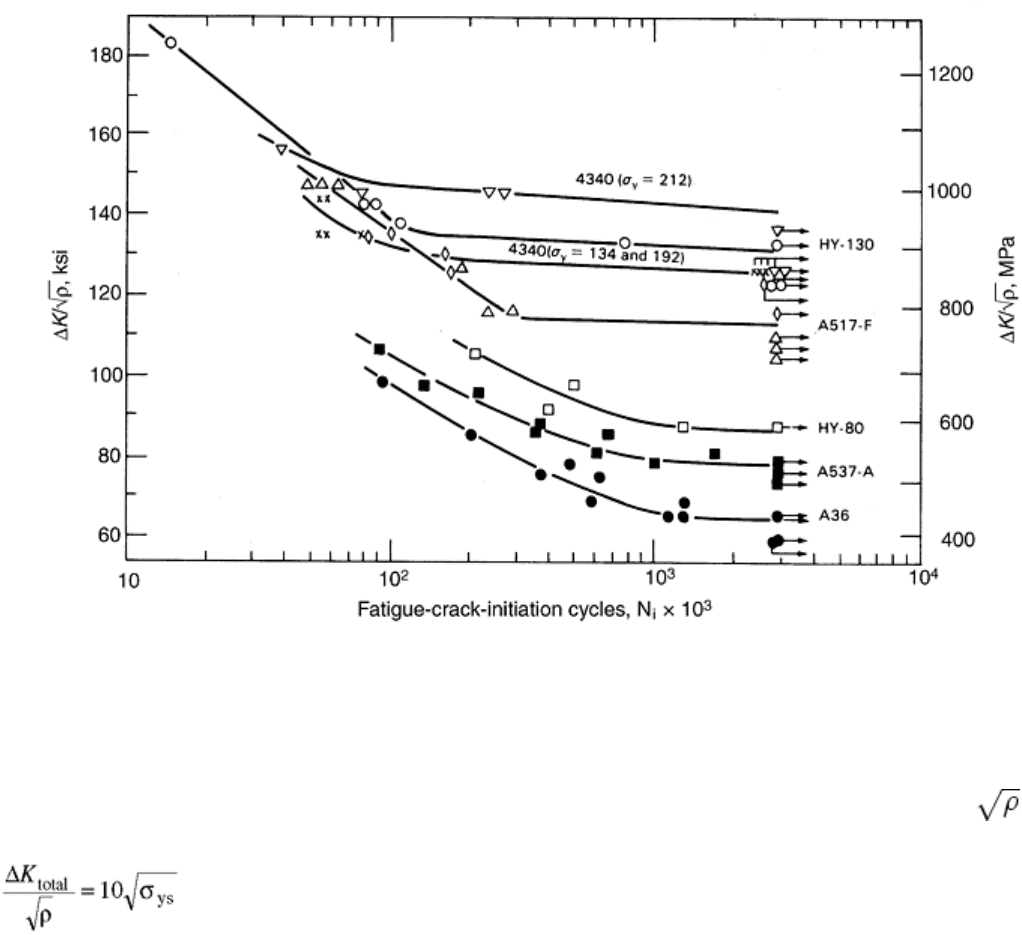
Fig. 4 Fatigue-crack-initiation behavior of various steels at a stress ratio of +0.1. Source: Ref 8
Finally, fatigue-crack-initiation data for various steels subjected to stress ratios (ratio of nominal minimum
applied stress to nominal maximum applied stress) ranging from -1.0 to +0.5 indicate that fatigue-crack-
initiation life is governed by the total maximum stress (tension plus compression) range at the tip of the notch
(Ref 9). The data presented in Fig. 5 (Ref 10) indicate that the fatigue-crack-initiation threshold, ΔK
I
/
th
, for
various steels subjected to stress ratios ranging from -1.0 to +0.5 can be estimated from
(Eq 2)
where ΔK
total
is the stress-intensity-factor range calculated by using the tension-plus-compression stress range,
and σ
ys
is the yield strength of the material.
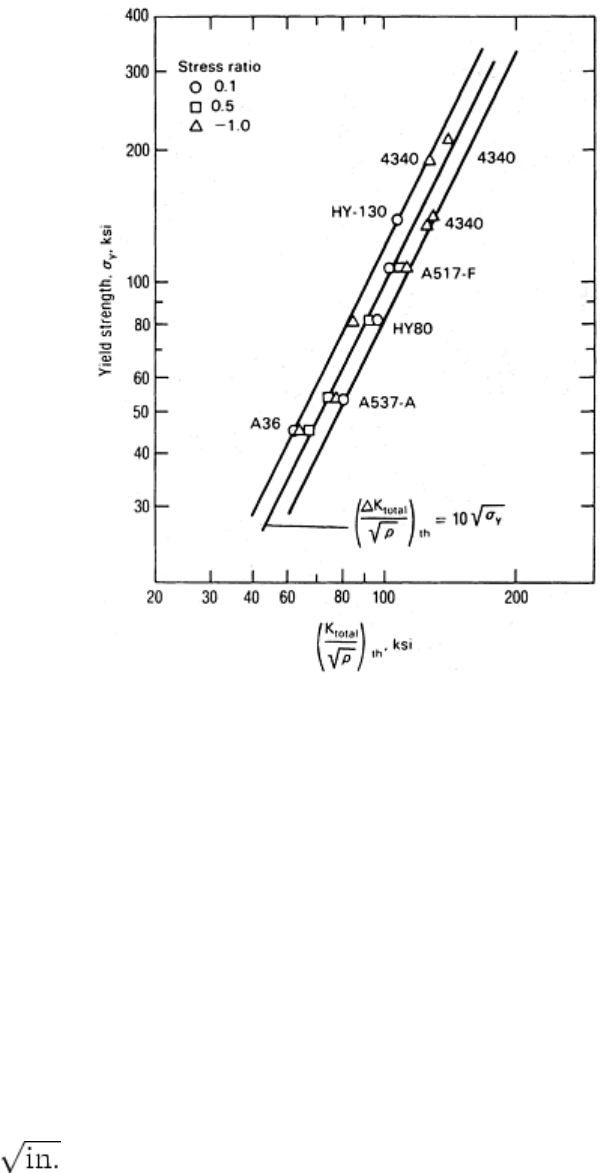
Fig. 5 Dependence of fatigue-crack-initiation threshold on yield strength
Fatigue-Crack Propagation. Extensive data have shown that the fatigue-crack-propagation behavior of metals is
controlled primarily by the stress-intensity-factor range, ΔK
I
. The fatigue-crack-propagation behavior of metals
can be divided into three regions, as shown in Fig. 6 (Ref 11). The behavior in region 1 exhibits a fatigue-crack-
propagation threshold, ΔK
th
, which corresponds to the stress-intensity-factor range, below which cracks do not
propagate under cyclic-stress fluctuations. An analysis of experimental results published on nonpropagating
fatigue cracks shows that conservative estimates of ΔK
th
for various steels subjected to different stress ratios, R,
can be predicted (Ref 8) from:
ΔK
th
= 6.4(1 - 0.85R)
for
R ≥ + 0.1
(Eq 3a)
and
ΔK
th
= 5.5 for R < +0.1
(Eq 3b)
where ΔK
th
is in ksi
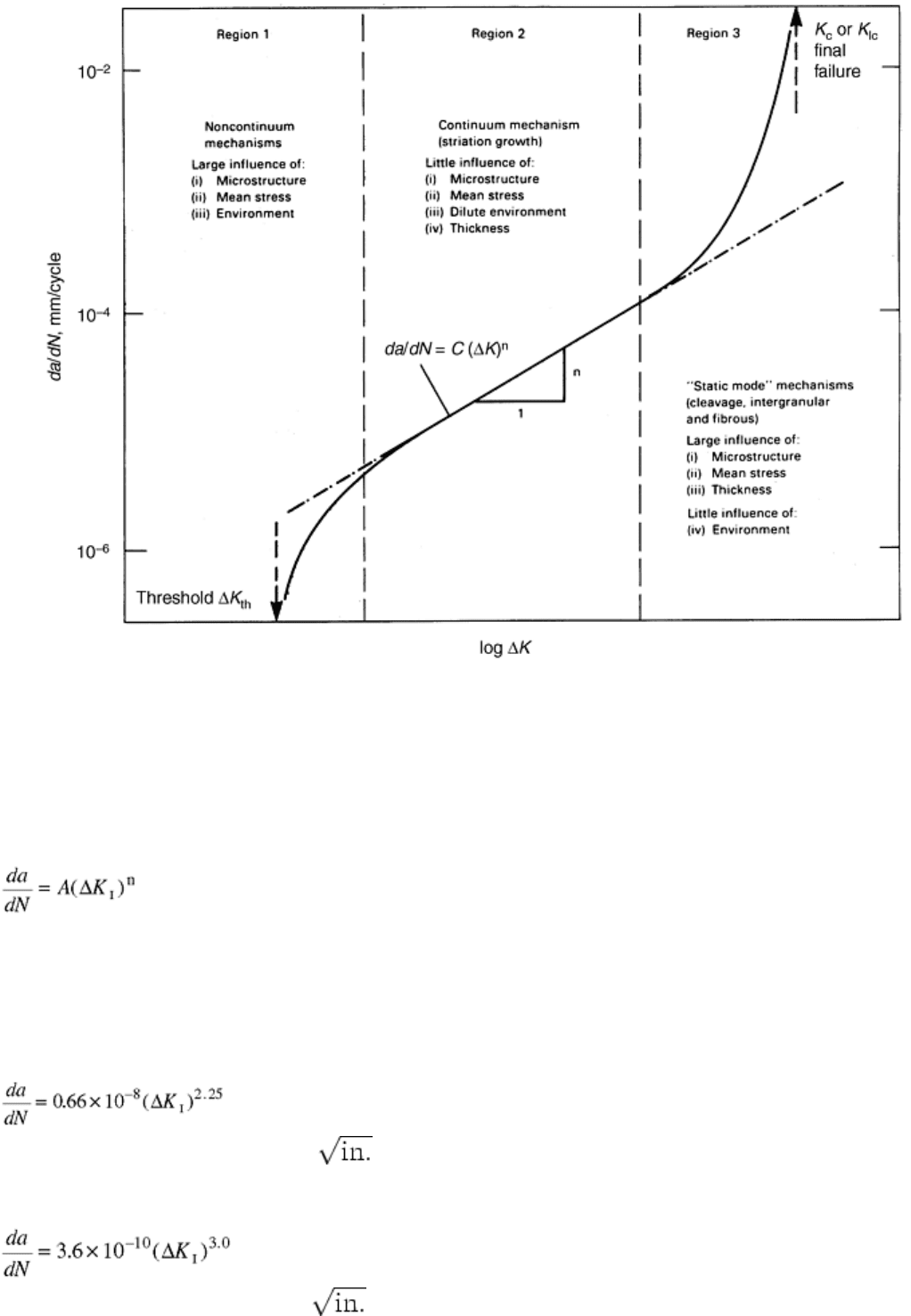
Fig. 6 Schematic illustration of variation of fatigue-crack-growth rate, da/dN, with alternating stress
intensity, ΔK, in steels, showing regions of primary crack-growth mechanisms. Source: Ref 11
Equation 3a and 3b indicates that the fatigue-crack-propagation threshold for steels is primarily a function of
the stress ratio and is essentially independent of chemical or mechanical properties.
The behavior in region 2 (Fig. 6) represents the fatigue-crack-propagation behavior above ΔK
th
, which can be
represented by the power-law relationship:
(Eq 4)
where a is crack length, N is number of cycles, and A and n are constants.
Extensive fatigue-crack-growth-rate data for various steels show that the primary parameter affecting growth
rate in region 2 is the stress-intensity-factor range, and that the mechanical and metallurgical properties of these
steels have negligible effects on the fatigue-crack-growth rate in a room-temperature air environment. The data
for martensitic steels fall within a single band, as shown in Fig. 7 (Ref 8), and the upper bound of scatter can be
obtained (Ref 8) from:
(Eq 5)
where a is in inches and ΔK
I
is in ksi Similarly, as shown in Fig. 8 (Ref 8), data for ferrite-pearlite steels
fall within a single band (different from the band for martensitic steels), and the upper bound of scatter can be
calculated from:
(Eq 6)
where a is in inches and ΔK
I
is in ksi
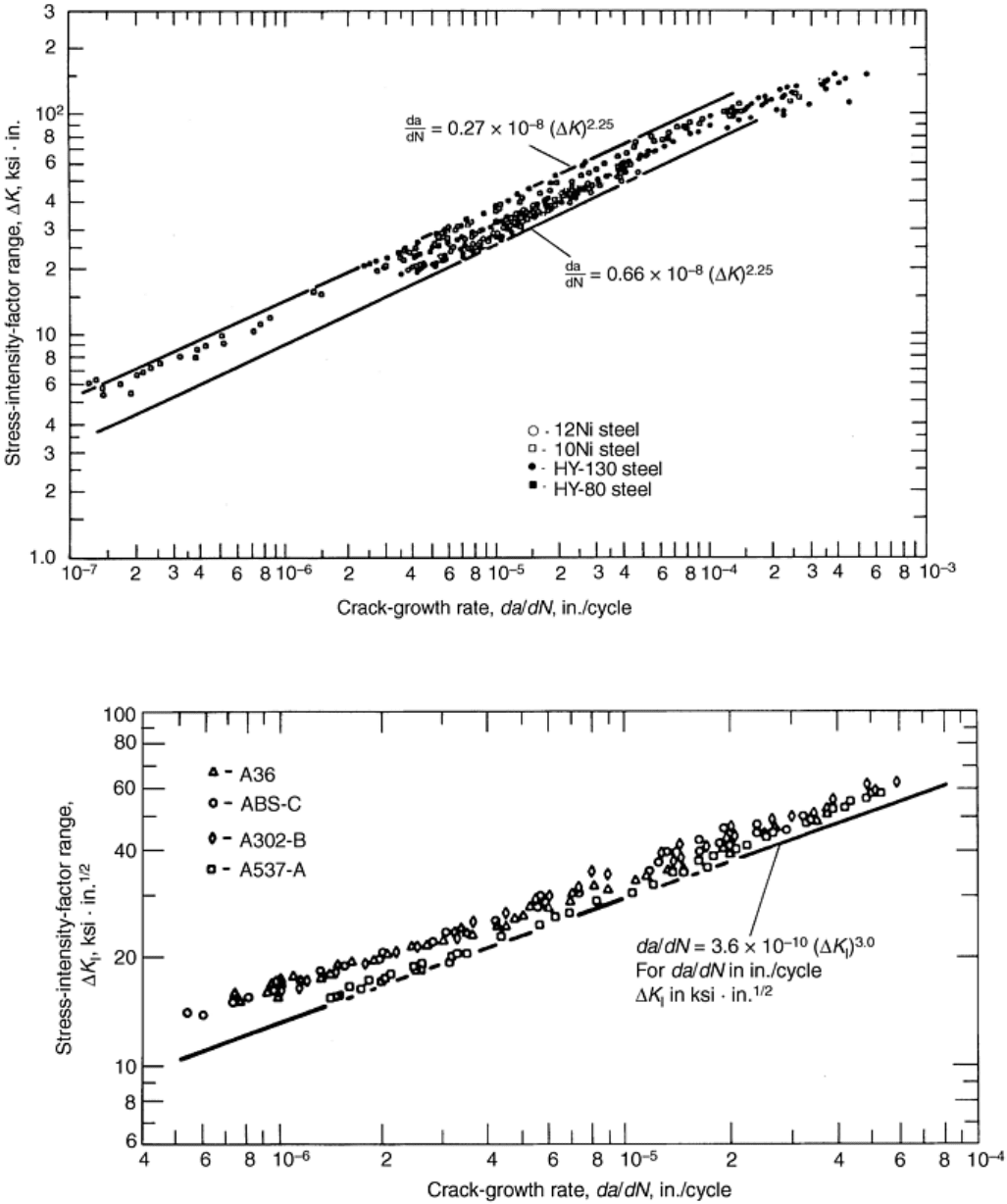
Fig. 7 Summary of fatigue-crack-growth data for martensitic steels. Source: Ref 8
Fig. 8 Summary of fatigue-crack-growth data for ferrite-pearlite steels. Source: Ref 8
The stress ratio and mean stress have negligible effects on the rate of crack growth in region 2. Also, the
frequency of cyclic loading and the wave form (sinusoidal, triangular, square, or trapezoidal) do not affect the
rate of crack propagation per cycle of load for steels in benign environments (Ref 8).
The acceleration of fatigue-crack-growth rates that determines the transition from region 2 to region 3 appears
to be caused by the superposition of a brittle or a ductile-tearing mechanism onto the mechanism of cyclic
subcritical crack extension, which leaves fatigue striations on the fracture surface. These mechanisms occur
when the strain at the tip of the crack reaches a critical value (Ref 8). Thus, the fatigue-rate transition from
