ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

Fig. 5 Three test-method configurations for fracture-toughness testing of ceramics included in ASTM C

1421. SCF, surface crack in flexure; SEPB, single-edge precracked beam; CNB, chevron notched beam

In the case of the single-edge precracked beam (SEPB) test specimen, prior to fracture testing, a compression

bridge anvil is used with the 3 by 4 mm (0.12 × 0.16 in.) cross section “bend bar” test specimen to produce

precracks from either a saw notch or a series of Vickers indentations. The precracked test specimen is then

fracture tested in either three- or four-point flexure (20 by 40 mm, or 0.8 × 1.6 in., inner/outer spans in four-

point flexure is recommended, although outer spans as short as 16 mm, or 0.6 in., in three-point flexure are

permissible). Various methods are suggested for determining conditions of instability, stable crack extension,

and other anomalies that can affect the test results.

Requirements for the precrack include the following:

• Inclination of the precrack front must be a

- a

min

< 0.1 a

, where a

and a

min

are the average and

minimum precrack lengths, respectively.

• The inclination of the propagation direction on the bottom surface and both sides of the specimen is ≤5°.

• The precrack length is between 0.35W and 0.60W, where W is the test specimen height.

For three-point flexure, the fracture toughness by the SEPB method is calculated as:

(Eq 10)

where K

Ipb

is the fracture toughness (in MPa ) using the SEPB method, P

max

is the maximum force (in

newtons) at fracture, S

is the outer support span (in meters), B is the test specimen breadth (in meters), W is the

test specimen height (in meters), a is the precrack length (in meters), and g is the geometry correction factor

that depends on the three-point flexure geometry (Ref 17, 18).

For four-point flexure, the fracture toughness by the SEPB method is calculated as:

(Eq 11)

where S

is the inner support span (in meters) and f is the geometry correction factor that depends on the four-

point flexure geometry (Ref 17, 18).

In the case of the surface crack in flexure (SCF) test specimen, a Knoop indenter is used to create a

semielliptical surface precrack. An essential step in this method is the removal of residual stresses induced by

the indenter. Grinding and polishing are recommended whereas annealing is not because it can lead to crack

healing and crack tip blunting. The precracked test specimen is then fracture tested only in four-point flexure

(20 and 40 mm, or 0.8 and 1.6 in., inner and outer spans, respectively). Post-test fractography is necessary to

determine the precrack size for the calculation of the fracture toughness. It has been argued that the SCF

method may give results representative of the intrinsic fracture resistance of the material because the induced

flaw can be on the order of the intrinsic flaws (Ref 9).

The fracture toughness by the SCF method is calculated as:

(Eq 12)

where K

Isc

is the fracture toughness (in MPa ) using the SCF method and Y is the greater of two possible

geometry correction factors:

(Eq 13a)

(Eq 13b)

where M, H

, H

, Q, and S are dimensionless functions based on an assumed half semiellipsed precrack shape

(Ref 17, 18).

In the chevron notched beam (CNB) test specimen, a V-shaped notch is cut in the “bend bar” with the tip of the

V oriented to the tensile stress during fracture testing. The advantage of the CNB test is that no prior

precracking is required. Instead, the crack initiates at the tip of the chevron during testing. The crack then

propagates through the chevron in a stable manner because the chevron presents an ever-widening crack front

to the propagating crack. Examination of the loading curves provides an indication of stable fracture (e.g.,

smooth, nonlinear rollover), a necessary requirement for a valid CNB test. Either three- or four-point flexure is

allowed for the CNB with allowable test geometry parameters (L, W, S

, and S

) dependent on the test

configuration chosen (A, B, C, or D) (Ref 18). Valid tests must have chevron notch planes that meet within

three notch thicknesses; the tip of the chevron must be less than 2% of the test specimen breadth, B, from the

centerline; and the difference between the two chevron length measurements and the average of the chevron

length must be less than 2% of the test specimen height, W.

The fracture toughness by the CNB method is calculated as:

(Eq 14)

where K

Ivb

is the fracture toughness (in MPa ) using the CNB method and is the minimum stress

intensity factor coefficient for the relevant geometry (Ref 17, 18).

Interferences addressed in ASTM C 1421 include slow crack growth (i.e., environmentally assisted crack

growth), R-curve effects, and stability. Other methods considered but not addressed in the standard include

indentation strength in bending (ISB), indentation fracture (IF), double cantilever beam (DCB), and single-edge

notched beam (SENB). Discussions of why these methods were not included in the ASTM standard are

provided elsewhere (Ref 9).

JIS Standard for Fracture Toughness of Ceramics. In 1990, the Japanese Industrial Standards Committee (JISC)

adopted the Japanese Industrial Standard (JIS) R1607 “Testing Methods for the Fracture Toughness of High

Performance Ceramics” (Ref 19). This standard contains two test methods for the determination of the fracture

toughness of ceramics: SEPB and IF.

Similar to the ASTM SEPB method, either Vickers indentations or a straight notch can be used as “starters” in

the 3 by 4 mm (0.12 × 0.16 in.) cross section bar prior to the use of the compression bridge anvil. Unlike the

ASTM SEPB method, after introducing the precrack, the fracture test is conducted only in three-point flexure

using either 16 or 30 mm (0.63 or 1.18 in.) outer spans. Requirements for the precrack include the following:

• The length variation and inclination of the precrack front must be (a

max

- a

min

)/2 < 0.1, where a

max

and

min

are the maximum and minimum precrack lengths, respectively.

• The inclination of the propagation direction on the bottom surface and both sides of the specimen is

≤10°.

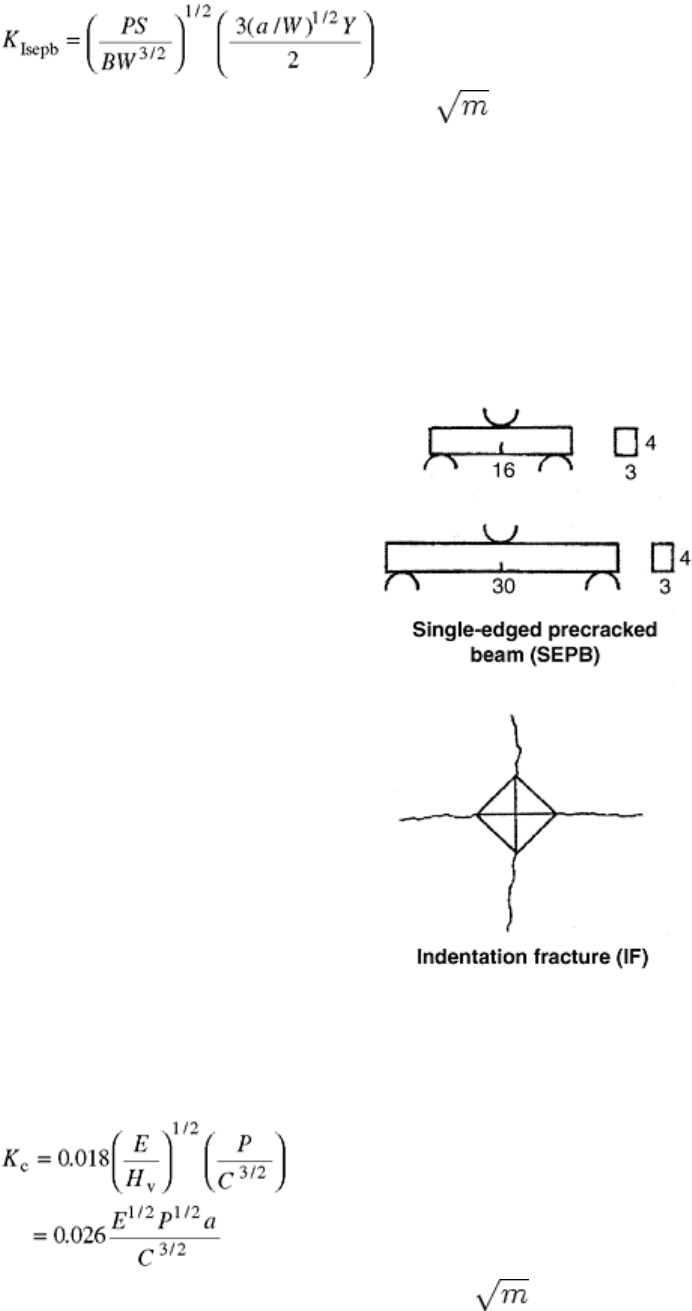
• The precrack length is between 1.2 and 2.4 mm (0.05 and 0.09 in.).

The fracture toughness by the SEPB method is calculated as:

(Eq 15)

where K

Isepb

is the fracture toughness (in MPa ) using the SEPB method (Ref 19). The average of five valid

tests is reported.

For the IF method, a Vickers hardness tester “at a large load” is used to create the impression (cracked from

corners), as shown in Fig. 6. Within 10 minutes after the creation of the indentation, both diagonal dimensions

(two corner crack lengths combined with the indentation diagonal length) are measured. The corner cracks must

satisfy the following conditions:

• Cracks start at the corner of the indentation and propagate in the diagonal direction.

• Lengths of any two cracks normal to each other differ by less than 10% of the average crack length.

• Any crack length is at least 2.5 times the diagonal length of the indentation.

Fig. 6 Two methods for fracture-toughness testing of ceramics contained in JIS R1607-90. Dimensions in

millimeters. Source: Ref 19

The quasi-fracture toughness is calculated as:

(Eq 16)

where K

is the quasi fracture toughness (in Pa ) using the IF method, H

is the Vickers hardness (in

pascals), C is half the average crack length (in meters), and a is half the average diagonal length of the

indentation (in meters). There is considerable controversy surrounding the result of the IF for accurate and

precise measurements of fracture toughness. Two obvious concerns are the choice of the “calibration constant,”

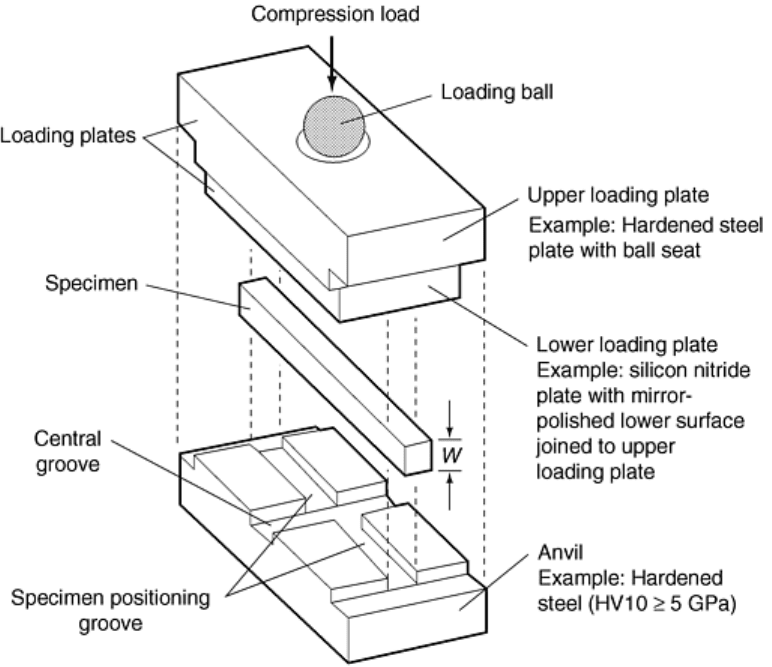
which is 0.018 in Eq 18 but could be one of over 19 different values (Ref 20, 21) and the highly subjective

estimate of the final crack tip. Even JIS R1607 states that the result of the IF method cannot be strictly

considered a fracture toughness.

ISO Standard for Fracture Toughness of Ceramics. The International Organization for Standardization (ISO)

made significant progress in 1999 when ISO DIS15732, “Fine Ceramics (Advanced Ceramics, Advanced

Technical Ceramics)—Test Method for Fracture Toughness of Monolithic Ceramics at Room Temperature by

Single Edge Pre-Cracked Beam (SEPB) Method” (Ref 22) was approved. In addition, a new working group has

introduced an advanced draft of an SCF fracture testing method (Ref 23). ISO Technical Committee (TC) 206

has oversight of both these efforts, although in this article only ISO DIS15732 is discussed in detail because

many of the essential aspects of the current draft of the SCF test method are similar to the SCF test method

contained within ASTM C 1421. “Harmonization” of existing national and regional standards, not development

of completely new standards, is one of the charter goals of ISO TC206.

ISO DIS15732 is a combination of the two existing national standards containing the SEPB fracture test

method: ASTM C 1421 and JIS R1607. Because the proper introduction of the precrack is critical to the success

of the SEPB method for both ASTM and JIS standards, explicit directions and illustrations are provided in an

annex (Fig. 7). Both three- and four-point flexure are allowed in certain outer and inner support spans, again, as

contained in both the ASTM and JIS standards (Fig. 8). Also, as contained in the ASTM and JIS standards,

either a row of Vickers (or Knoop) indentations or a saw notch are allowed for the precrack starter. Similarly,

the cross section of the beam is 3 by 4 mm (0.12 × 0.16 in.) with minimum lengths ranging from 18 to 45 mm

(0.7–1.8 in.) depending on the testing configuration.

Fig. 7 Illustration of compression bridge anvil for fracture-toughness testing of ceramics in ISO DIS

15732. Source: Ref 22

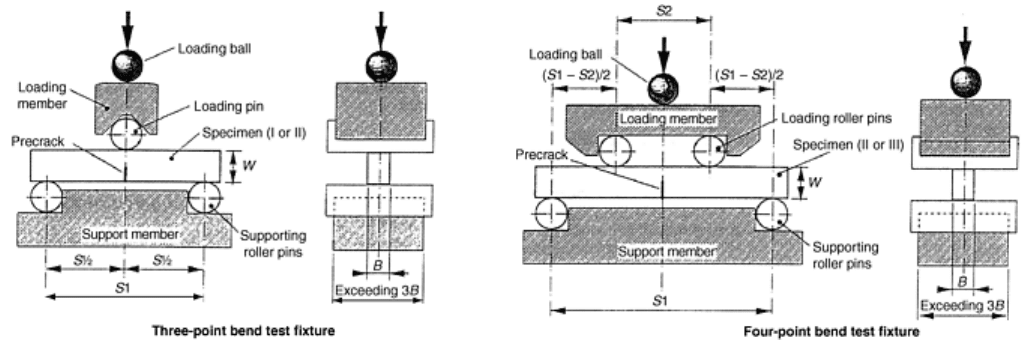
Fig. 8 Test configurations for ISO DIS 15732. For three-point bend (flexure), S1 can be 16 or 30 mm

(0.63 or 1.18 in.). For four-point bend (flexure), S1 can be 30 mm (1.18 in.) with S2 at 10 mm (0.39 in.), or

S1 can be 40 mm (1.57 in.) with S2 at 20 mm (0.79 in.). Source: Ref 22

Notable additions to ISO DIS15732 not contained in either the ASTM or the JIS standards are sections on

determining precrack length and stable crack growth using compliance changes and fractography. Additional

sections deal with permissible range of stable crack growth (≤2% of the average precrack length) and

permissible relative compliance change (≤10% of the ratio of precrack length to test specimen height).

Requirements for the precrack include the following:

• Length variation and inclination of the precrack front must be (similar to JIS R1607) (a

max

- a

min

)/2 <

0.1, where a

max

and a

min

are the maximum and minimum precrack lengths, respectively.

• The inclination of the propagation direction on the bottom surface and both sides of the specimen is ≤5°

for the three-point flexure geometries and ≤10° for the four-point flexure geometries (mixture of JIS

R1607 and ASTM C1421).

• The precrack length is between 0.35W and 0.60W, where W is the test specimen height (similar to

ASTM C1421).

Notes are provided regarding R-curve effects (the measured fracture toughness may be “artificially high” if

stable crack growth occurs after pop-in of the precrack) and slow crack growth effects (the measured fracture

toughness may be reduced because of environmentally assisted crack propagation).

The fracture toughness by the SEPB method is calculated using Eq 15 for the three-point flexure geometries

and Eq 11 for the four-point flexure geometries. Five or more valid test results are used in calculating an

average fracture toughness value.

CEN Standard for Fracture Toughness of Ceramics. Comité Européen de Normalisation (CEN) is the de facto

standards-writing body for the European Union. As of 1999, a pre-Euro Norm Voluntaire (preENV) had been

drafted indicating the intent to develop a seven-part fracture-toughness testing standard within CEN Technical

Committee (TC) 184 on Advanced Technical Ceramics. The first part of this standard is currently in draft form

and provides summaries of the six test methods contained in each of the following six sections, as well as

guidance to the user as to choice and application of a particular test method (Ref 24).

A pictorial summary of the six test methods is shown in Fig. 9; a summary and comparison are provided in

Tables 1 and 2, respectively. Note that with the exception of the IF method, all six methods use “bend-bar” test

specimen geometries. Of the six, the SEPB method is contained in the current ASTM, JIS, and ISO standards.

The CNB method is contained in the ASTM standard, as is the SCF method. The IF method is contained in the

JIS standard. Two methods not yet standardized are the single-edge V-notch beam (SEVNB) and the

indentation strength (IS) methods. These two methods are discussed briefly here.

Table 1 Methods for determining apparent fracture toughness using small test specimens

Method Description Calibrations

Uncertainties or difficulties

Single-edge

precracked

beam (SEPB)

A flexural test in a

beam into the tensile

side of which a short

straight crack has

been introduced

Accurate calibrations

available for wide range of

precrack lengths. Fracture

toughness is determined at a

defined crack length.

Precracking requires some skill to

obtain straight-fronted cracks.

Results are influenced by rising

fracture-resistance behavior.

Chevron

notched beam

(CNB)

A flexural test in a

beam into the tensile

side of which a short

straight crack has

been introduced

Accurate calibrations

Fracture toughness is calculated at

assumed crack length. Crack

initiation may be difficult in some

materials due to machining residual

stresses. Result may be influenced

by rising fracture resistance

behavior.

Surface crack

in flexure

(SCF)

A flexural test in a

beam into the tensile

side of which a short

straight crack has

been introduced

Accurate calibrations

assuming the precrack shape

approximates to an ellipse

after removal of surface

damage region

Requires observation and

measurements of precrack

dimensions, which may not be

clearly visible. Limited to materials

in which indentation produces

good-quality cracks. Result typical

for small cracks

Single-edge V-

notch beam

(SEVNB)

A flexural test in a

beam into the tensile

side of which a short

straight crack has

been introduced

Accurate calibrations

assuming sharp crack (same

as SEPB)

Assumes that if the tip radius of the

sharp notch is of the order of the

grain size, then the notch is

equivalent to a sharp crack and the

SEPB calibration can be used

Indentation

fracture (IF)

A flexural test in a

beam into the tensile

side of which a short

straight crack has

been introduced

Poor calibrations owing to

uncertainties in stress fields

developed by indentation

methods of cracking. Wide

variety of different

calibrations available

Effective only in materials that do

not chip or flake when indented.

Inappropriate for tough or porous

materials. Result typical for small

cracks

Indentation

strength (IS)

A flexural test on a

beam into the

tensile side of which

has been placed an

indentation

Poor calibrations owing to

uncertainties in residual

stress fields developed by

indentations that are not

removed

Reproducible test if well-defined

cracks are developed by

indentation. Result typical for small

cracks, but may not be indentation-

force dependent. Inappropriate for

porous materials

Adapted from Ref 24

Table 2 Comparison of fracture-toughness test methods

Test method

Criterion

SEPB CNB SCF SEVNB

(a)

Confidence in

calibration

(b)

Good Good Good Good Poor

Poor

Relative ranking of

materials

Yes Yes Yes Yes Possible for

similar

materials

Yes

Long-crack fracture

toughness

Yes Yes No No No

Determine R-curve Yes No No No

(c)

effects

Short-crack fracture

toughness

No No Yes Yes

(d)

Yes

Fast-fracture fracture

toughness

Yes No Yes Yes Yes

Yes

Controlled-crack-

growth fracture

toughness

Possible Yes No No No

Low scatter results Possible Possible Yes Yes No

Yes

Fine-grained

materials

Yes Yes Yes Yes Yes

Yes

Coarse-grained

materials

Yes Yes Unlikely Yes Unlikely

Unlikely

OK if K

< 6

MPa

Yes Yes Yes Yes Yes

Yes

OK if K

> 6

MPa

Yes Yes Possible

(e)

Yes No

Sensitive to crack

growth before

fracture

Yes Uses a

moving

crack front

Yes Possible Yes

Yes

Sensitive to

notch/precrack

geometry

Possible Probable Yes Possible for

fine-grained

materials

Not

appropriate

Not

appropriate

Suitable for elevated

temperature

Yes

(f)

Yes Yes

(f)

Yes No

Possible

(f)

Cost of effort to do

tests

High Medium High Medium Low

Medium

Cost of facilities to

do tests

Medium

Medium High Medium Low Medium

(a) Attributes given are for notch root radii of ≤5 μm.

(b) On a fracture mechanics basis alone, the quality of the experimental result is influenced by the nature of the

material.

(d) If the notch is considered to have a short flaw at its tip, R-curve effects are avoided.

(e) Increasing likelihood of poor precrack generation with increasing fracture toughness.

(f) Upper temperature limit is crack-tip blunting, crack healing, and/or oxidation. Adapted from Ref 24

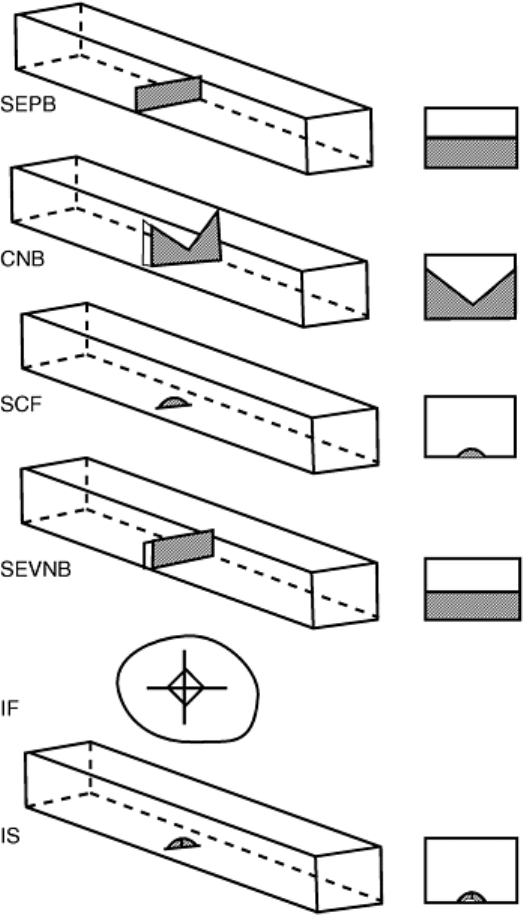
Fig. 9 Pictorial summary of test methods contained in CEN TC184 draft fracture toughness standard

(Ref 24). SEPB, single-edge precracked beam; CNB, chevron notched beam; SCF, surface crack in

flexure; SEVNB, single-edge V-notched beam; If, indentation fracture; IS, indentation strength

The SEVNB method is a variation of the single-edge notch beam (SENB) method, which has been a mainstay

of the fracture testing community since before the introduction ASTM E 399. However, in brittle materials, the

SEVNB addresses a problem that had long plagued the SENB method: how should a sharp crack at the tip or

root of the saw notch be introduced? No matter how thin the diamond saw blade (even 50–100 μm thick), a

blunt notch is still not an atomistically sharp crack, and, hence, without the introduction of a precrack at the

notch tip (e.g., fatigue precracking or SEPB compression bridge loading), the SENB test does not meet one of

the basic requirements for a fracture toughness test: a well-defined, atomistically sharp crack. When compared

to sharp-crack methods, blunt-notch methods tend to “overestimate” fracture toughness with results that are

often a function of notch thickness (e.g., see Ref 25 for a comparison of results for sharp-crack and blunt-notch

techniques for alpha silicon carbide).

What sets the SEVNB method apart from the usual SENB method is that after the initial notch is sawed into the

beam, the notch tip is “sharpened” (Ref 26, 27). In the latest rendition of the SEVNB method, a reciprocating

(either manual or mechanized) conventional razor blade is used, along with various grits of diamond paste, to

create the V at the tip of the saw notch (Ref 27). This V-notching technique tends to create notch root radii (or

damage zone) less than those that would make the measured fracture toughness a function of the notch width or

geometry. The SEVNB method produces precise and accurate results similar to sharp-crack methods (e.g.,

SEPB and SCF) without the need to precrack the test specimen (Ref 27). In addition, measurement of the notch

depth at fracture allows the use of the same well-established equations, such as those used for SEPB method

(e.g., Eq 11, 12, and 15) for calculating fracture toughness.

The IS method is based on the applications of Eq 1 and 4 to the flexural strength testing of flexural test

specimens that have been indented (either Knoop or Vickers) with ever-increasing indentation forces. The size

of the controlled indentation flaw increases with increasing indentation force. Therefore, for a material with a

deterministic fracture resistance, the measured flexural strength will decrease with increasing flaw size (or

increasing indentation force). The mathematics have been worked out relating fracture resistance, flexural

strength, and flaw size for sharp indenters producing median cracks (Ref 3).

The actual mechanics of the conducting test involve first placing one indentation each in a series of standard

flexure test specimens (each test specimen receives one indentation at one indentation force), such as those

specified in ASTM C 1161 (Ref 28) at ever-increasing indentation forces using either a Knoop or Vickers

indenter. A standard flexural strength test is then conducted, preferably in four-point flexure to avoid the

necessity of trying to align the small indentation with the nose of the loading support in three-point flexure. For

four-point flexure, the flexural strength is calculated as:

(Eq 17)

where S

is the flexural strength and P

is the force at fracture (typically maximum force for a brittle material).

The fracture toughness using the indentation strength method for the particular test can then be calculated using

the relation (Ref 29):

(Eq 18)

where P is the indentation force.

Obvious advantages of the IS method are that it involves readily available flexure test specimens and test

standards for both flexure strength and indentations. In addition, the IS method does not require a subjective

measure of crack size (from the viewpoint of the fracture-mechanics community, this is also an obvious

weakness) (Ref 2). Another weakness is that hardness and elastic modulus need to be measured separately. A

final point is that the constant 0.59 in Eq 18 as determined from logarithmic regression analysis (Ref 2) has an

estimated standard deviation of 0.12 (a somewhat large source of variability for a “constant”). While the IS

method is attractively simple, relative measurements on a given material “are typically reliable to much better

than 20%” (Ref 3), making the results of limited value compared to some of the other methods discussed up to

this point.

Other Test Methods for Fracture Toughness at Ambient Temperature

Many other successful methods for determining fracture toughness of brittle materials (not yet standardized)

have been introduced and refined over the past several years. Some of the more popular methods are discussed

in the following sections. Note that these discussions are limited to sharp-crack methods because of the

limitation of methods using blunt notches.

The double torsion (DT) method was once seen as a strong contender for a standard test method (Ref 4, 7, 8, 9,

and 10). This method (Fig. 10) allows the use of a variety of basic specimen shapes and test geometries,

although the most common is a long, thin plate with a side groove cut along its length to guide and crack

(although there is evidence that with good alignment, better results are obtained without the groove (Ref 31).

Ball-bearing supports tend to minimize friction and help alignment. Various analyses have shown that the

applied stress intensity factor is independent of crack length over the dimensionless crack length range of 0.55

to 0.65 a/W (Ref 4). One formulation for stress intensity factor for determining fracture toughness using the DT

method is (Ref 30):

(Eq 19)

where W

is half the test specimen width minus half the notch width, d is the total thickness, d

is the notch

depth, and ξ is a correction factor for thick test specimens such that ξ = 1 - 0.6302t + 1.20t exp (-π/τ) where t =

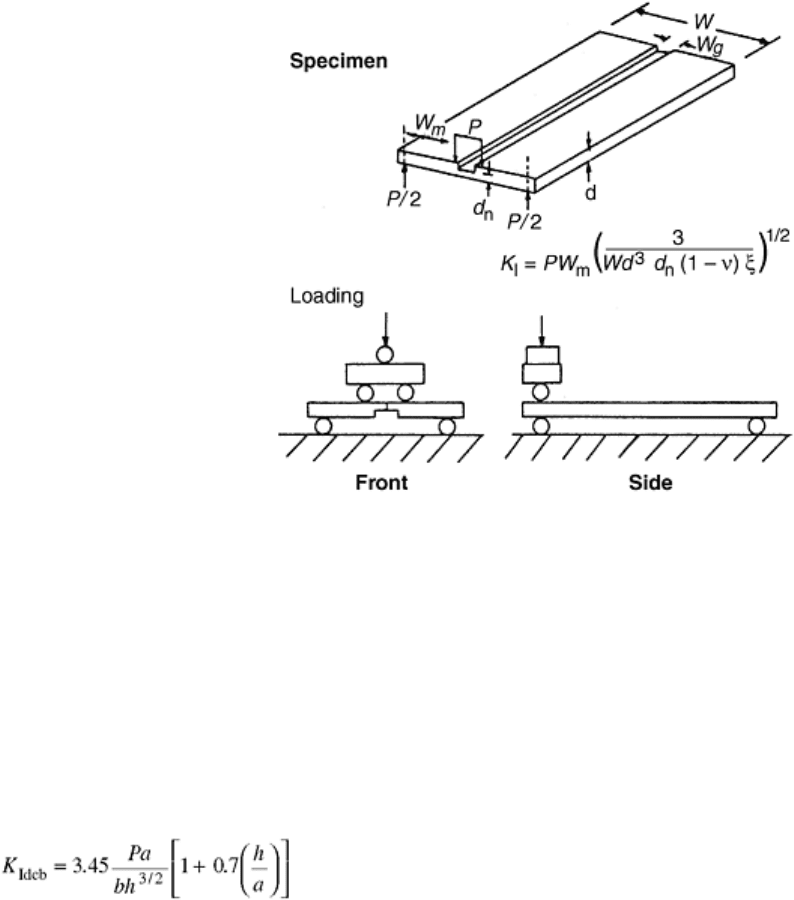
2d/W and W is the total width of the test specimen. Although the three-dimensionality of the crack front in the

DT test specimen has lead to some controversy about whether Eq 19 really represents a mode I stress intensity

factor, evidence exists that K

Idt

for various brittle materials compares well to other sharp-crack mode I methods

(Ref 25, 30). Obvious advantages of the DT method include the simple loading configuration, its constant stress

intensity factor geometry, simple test specimen geometry, and stable crack propagation configuration. Some

disadvantages include the relatively large volume of test material (compared to a simple flexure bar) required

for a single test, the more complicated arrangement of ball bearings and other components for supports, the

curved crack front, and concerns about the three-dimensionality of the crack tip.

Fig. 10 Schematic illustration and nomenclature for double torsion (DT) fracture-toughness test

methods. Source: Ref 30

The double cantilever beam (DCB) test method has been part of fracture mechanics in various forms since the

inception of the discipline. Indeed, variations of the DCB method even appear in ASTM E 399 for fracture

toughness testing of metals. A unique aspect of the DCB test method applied to brittle materials is the method

of load application that can have a variety of forms, as shown in Fig. 11. The applied-load method can be

particularly troublesome in brittle materials that are susceptible to tensile forces. However, the compressively

loaded wedge-loading method and the compressively loaded applied-moment method are suited to testing

brittle materials. Often side grooves are used to guide the crack longitudinally. For the applied-load geometry,

the stress intensity factor and subsequent fracture toughness have been formulated as (Ref 4):

(Eq 20)

where h is half height of the test specimen, b is thickness of the test specimen, and a is the crack length. Some

advantages of this geometry are that for some cases the stress intensity factor is independent of crack length

(e.g., tapered DCB or applied moment DCB), test specimen preparation can be simple, material usage is

efficient, and the loading configuration can be simple. The primary disadvantage is that a sharp crack needs to

be introduced to avoid problems of initiation and propagation of a crack from the blunt notch.