ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

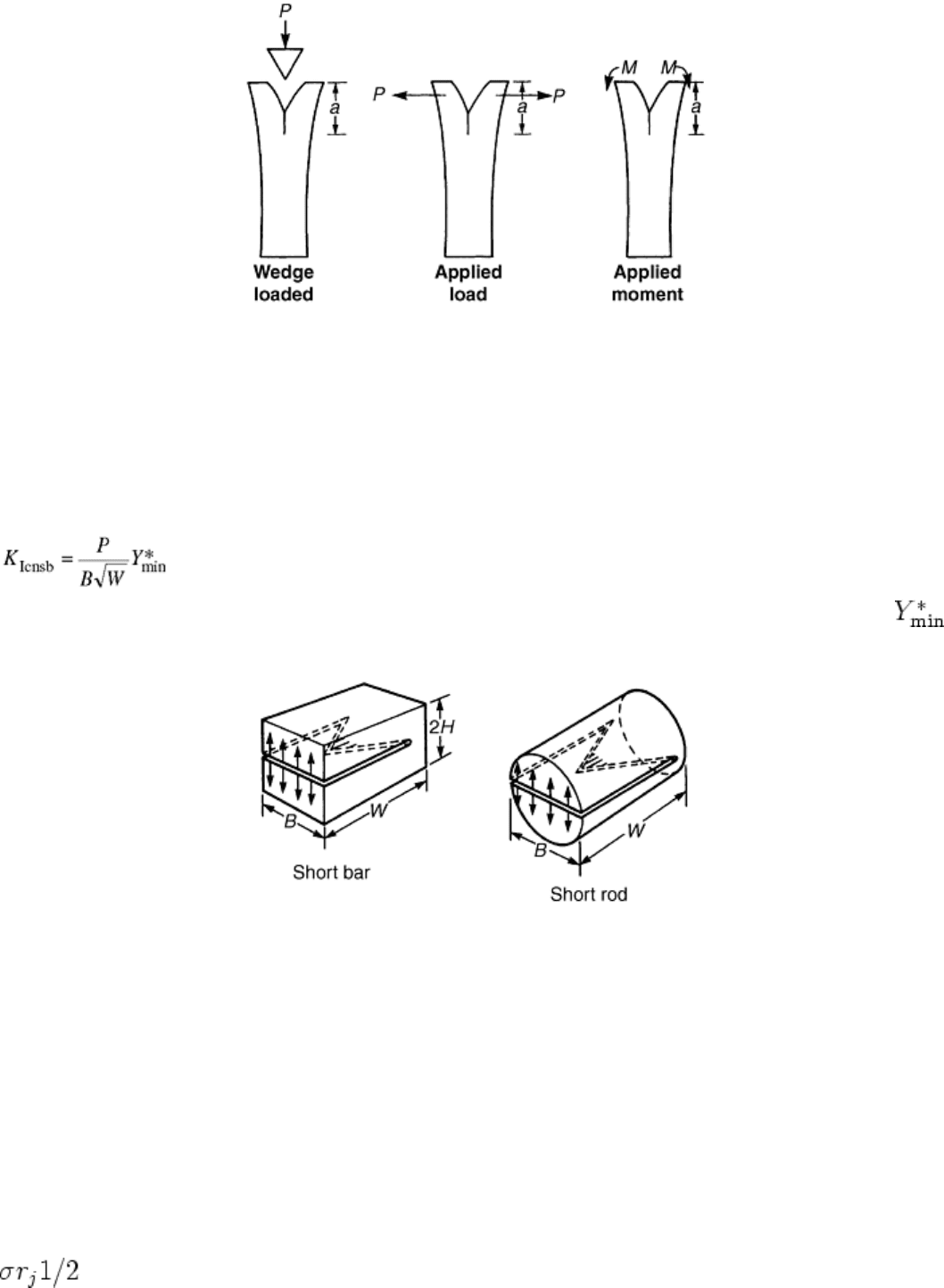
Fig. 11 Double cantilever beam (DCB) fracture test methods

Chevron notched short-rod and short-bar (CNSR and CNSB) test methods (Fig. 12) have many of the

advantages of the CNB test method: simple notch preparation, in situ (automatic) crack initiation at the tip of

the chevron, and inherent stable crack propagation in the chevron. However, an additional advantage of the

CNSR and CNSB geometries is the efficient use of material because the volume of material needed to support a

flexural test specimen is avoided. For the CNSB geometry, a suggested formulation for the stress intensity

factor and subsequent fracture toughness can be determined as (Ref 4, 32):

(Eq 21)

where P is the applied force, W is length of the test specimen, B is thickness of the test specimen, and is

the minimum geometry correction factor for the chevron notch geometry. A disadvantage of the CNSR and

CNSB test method is the tensile loading required for the fracture test, as shown in Fig. 12.

Fig. 12 Examples of chevron notched short bar (CNSB) and chevron notched short rod (CNSR) test

specimens. Source: Ref 4, 32

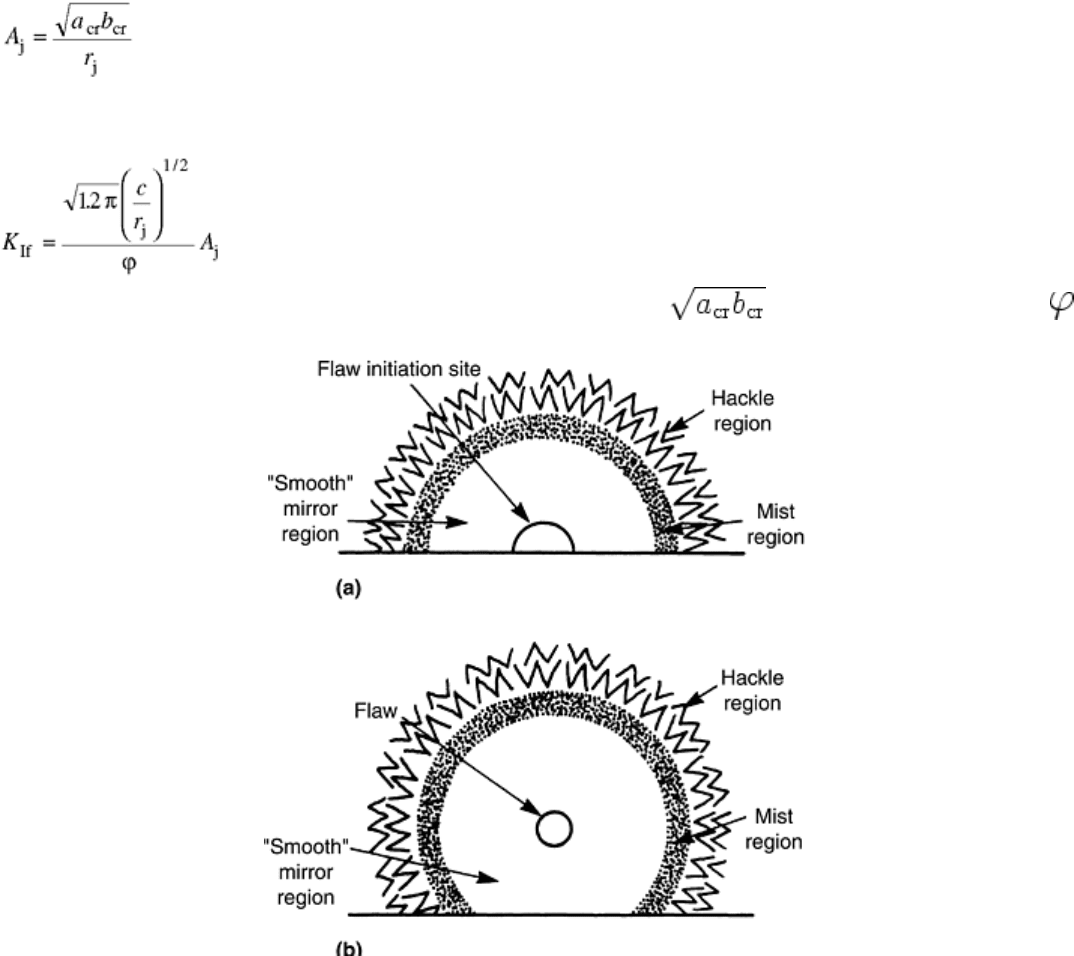
Fractographic methods (Ref 33, 34) applied to strength tests of intrinsically flawed test specimens involve

interpretation of fracture features, quantification of the type and size of the strength-limiting flaws,

determination of the applied stress at the flaw suite, and, finally, the calculation of the fracture toughness of the

material. It is important to realize that it is usually difficult to directly measure flaws initiating at fracture sites

(Ref 35 contains information on fractographic aspects of brittle materials). However, as a consequence of the

rapid crack propagation during brittle fracture, the fractured region around flaws often exhibits distinct regions

(Fig. 13): flaw origin, fracture mirror (smooth region surrounding the origin), mirror (radial ridges surround the

mirror), and hackle (rough ridges surrounding the mirror. Crack branching can exist outside the hackle region

as well. A quantitative relationship exists between the stress at the fracture and the distance from the flaw to

each of the boundaries of this fracture region such that (Ref 33):

= A

(Eq 22)

where σ is the stress at fracture, r

is the distance to a particular boundary, and A

is the corresponding mirror

constant such that

(Eq 23)

where a

is the failure-initiating flaw depth, b

is its half depth, and r

is the relation of fracture mechanics to

fractography is given as (Ref 32):

(Eq 24)

where K

is the fracture toughness determined from fractography, c = , as illustrated in Fig. 14, and

is an elliptical integral of the second kind that accounts for degree of ellipticity of the flaw.

Fig. 13 Nomenclature for fracture features. (a) Surface flaws. (b) Volume flaws. Source: Ref 4, 34

Fig. 14 Schematic of fracture surface of brittle materials showing the idealized preexisting flaw of depth

and half-width b

and the failure-initiating critical flaw of depth a

and half-width b

. For rapid

loading, a

and b

should be nearly coincident with a

and b

. The fracture-mirror radii boundaries are

also shown in the figure: r

, mirror-mist; r

, mist-hackle; and r

, macroscopic crack branching. For some

conditions, r

and r

cannot be distinguished. σ is the fracture stress. Source: Ref 33

Evaluation of Fracture-Toughness Test Results

Although many examples exist in the literature of small batches of fracture toughness results for fracture

resistance testing using a wide variety of methods applied to brittle solids, it is only recently that results are

beginning to appear combining statistically significant sample sets of results for well-documented materials

fracture tested using accepted and/or approved standardized test methods. For example, ASTM C 1421 (Ref 18)

contains a precision and bias section that compares extensive results from various sources (including two

round-robin programs sanctioned by the Versailles Advanced Materials and Standards, or VAMAS,

organization) (Ref 36, 37) obtained using the test methods SEPB, SCF, and CNB detailed in ASTM C 1421

(although not necessarily the exact procedures). Two materials are highlighted: a sintered silicon carbide

[Hexoloy SA, Carborundum (now Ste. Gobain), Niagara Falls, New York] and a hot-pressed silicon nitride

[NC132, Norton Co. (now Ste. Gobain), Worcester, Massachusetts]. Each of these materials has a “flat” R-

curve and displays little environmental susceptibility at room temperature. The results, graphically illustrated in

Fig. 15 and 16, generally show the consistency of the fracture toughness measurements for two brittle materials

regardless of sharp-crack technique.

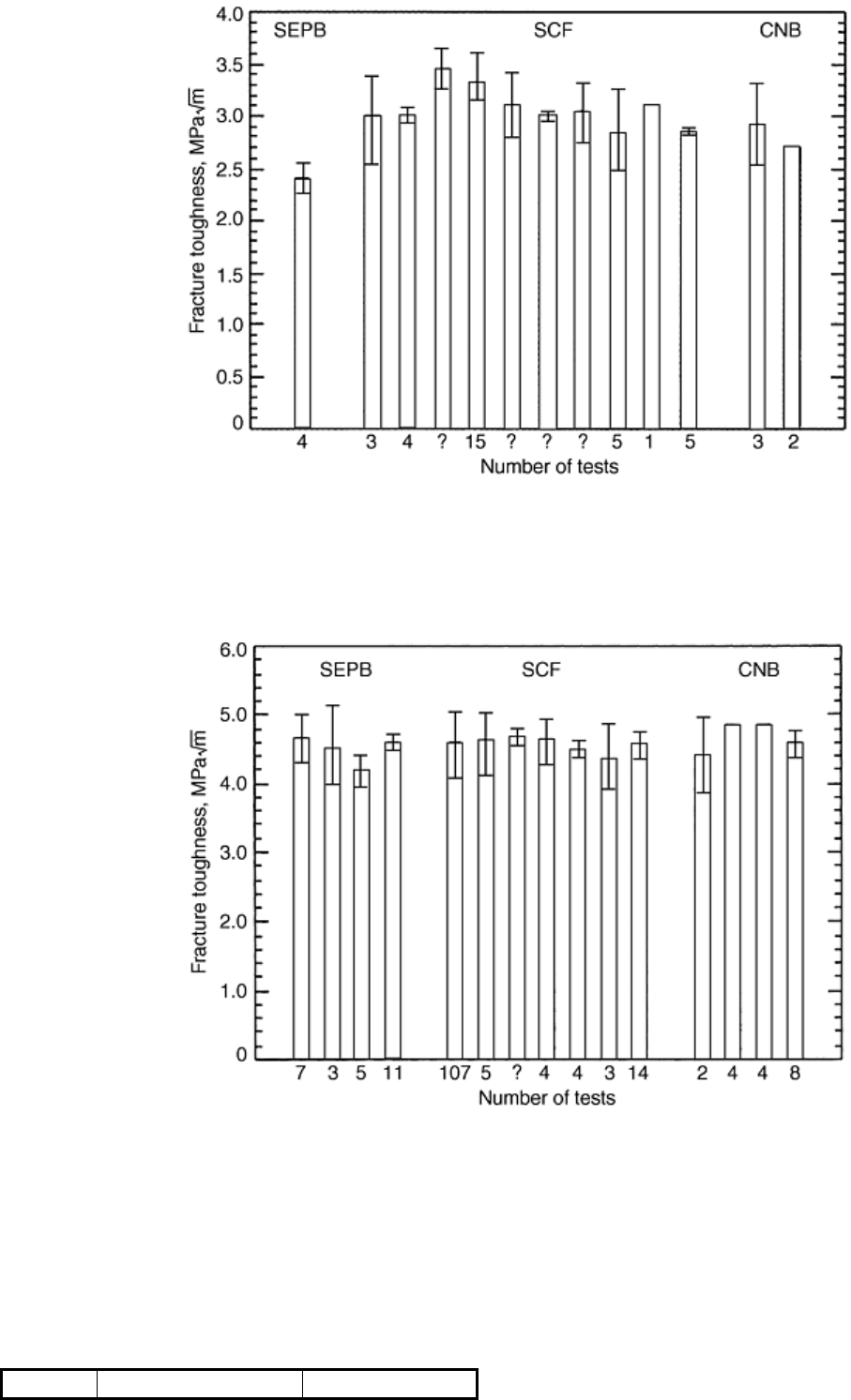
Fig. 15 Comparison of fracture-toughness test results from multiple sources for Hexoloy SA (sintered

alpha silicon carbide) using three test methods described in ASTM C 1421. Each bar represents the mean

plus or minus one standard deviation. SEPB, single-edge precracked beam; SCF, surface crack in

flexure; CNB, chevron notched beam. Adapted from Ref 18

Fig. 16 Comparison of fracture-toughness test results from multiple sources for NC 132 (hot-pressed

beta silicon nitride) using three test methods described in ASTM C 1421. Each bar represents the mean

plus or minus one standard deviation. SEPB, single-edge precracked beam; SCF, surface crack in

flexure; CNB, chevron notched beam. Adapted from Ref 18

A noteworthy use of ASTM C 1421 is to evaluate multiple billets of a standard reference material (SRM 2100,

National Institute Standards and Technology, Gaithersburg, Maryland, 1999) known as SRM2100, the same

hot-pressed silicon nitride as used in the VAMAS round robin and as shown in Fig. 16. For example, for billet

C of the SRM at room temperature, the results were:

Method

Fractire toughness,

No. of valid tests

MPa

SCF K

Isc

= 4.58 ± 0.16

(a)

CNB K

Ivb

= 4.60 ± 0.13

(a)

SEPB K

Ipb

= 4.58 ± 0.10

(a)

(a) Mean ± one standard deviation

This remarkable consistency of fracture toughness results for a single material confirms that the sharp-crack

methods contained within ASTM C 1421 have been “optimized” (Ref 9) such that genuine material variability

(e.g., billet-to-billet or batch-to-batch) can be discerned and quantified.

R-Curve Behavior at Ambient Temperature

R -curve behavior (i.e., increasing fracture resistance with crack extension, Fig. 3) for brittle materials, as

discussed briefly in the introduction, is often a result of interactions of the crack and microstructure. For

example, fracture process mechanisms as shown in Fig. 4 can be roughly divided into frontal and wake

mechanisms. But why measure R-curve behavior in brittle materials? The need to measure R-curve behavior

can include establishing the unequivocal starting point of the R-curve (i.e., intrinsic fracture resistance), R

, or it

can include determining the final steady-state fracture resistance, R

∞

, or it may include defining the behavior

between the extremes of the intrinsic and steady-state fracture resistance, R(c) which may also be a function of

crack shape, test specimen geometry, and testing parameters.

In metals, frontal mechanisms—specifically, plastic deformations in a region ahead of and near the crack tip—

are responsible for crack closure effects (Ref 38). For engineering analysis, elastic-plastic fracture-mechanics

concepts are usually applied, typically using K with a crack-size plasticity adjustment or the J-integral. It is

important to realize that R-curves are not material properties (unlike fracture toughness), but are instead related

to the testing conditions, including test rate and test specimen geometry (e.g., material thickness). Recently,

ASTM E 1820 “Standard Test Method for Measurement of Fracture Toughness” (Ref 16) was introduced as a

“unified” test method for fracture testing metals at room temperature. The test procedures of five other test

methods are contained in ASTM E 1820 to allow extraction of fracture resistance in terms of K, J, and crack-tip

opening displacement (CTOD) from a single test at room temperature. Three test specimens (similar to those

used in ASTM E 399) are described: SENB, compact tension (CT), and a disk-shaped compact tension (DSCT).

All require precracking, usually with cyclic loading, to promote fatigue crack initiation and propagation. Test

conditions and procedures are specific to the fracture parameter being measured. However, a compliance

method is described to establish in situ crack length during stable crack propagation.

ASTM E 1820 (Ref 16) was developed, and is appropriate, for measuring plane strain fracture toughness in

ductile metals but does not necessarily address the unique aspects of brittle solids. In addition, test specimens

are rather large, as are the notches, cracks, and precracks, presumably for ease of implementation as well as to

minimize the influence of dimensional variations on the repeatability and reproducibility of the fracture

resistance measurement.

Since the introduction of ASTM E 1820, standards-writing bodies worldwide have done little to introduce

standard R-curve test methods for brittle solids, particularly for advanced ceramics. Several possible

explanations exist for this:

• No single method for establishing R-curve behavior in brittle materials has stood out.

• No methodology has been established on how to use the measured R-curve behavior of brittle materials

(in engineering or materials design).

• It is not clear if current fracture toughness techniques really can establish the starting point of R-curve

behavior.

• R-curve behavior is not a material property because it is dependent on factors such as test specimen

geometry, crack history, test mode, and rate.

However, although no standardized test methods exist for R-curve behavior in brittle materials, many unique

and novel test methods have been reported. Often these methods focus on quantifying specific mechanisms

giving rise to R-curve behavior rather than measuring the R-curve itself. The following sections, while not

intended to be an exhaustive listing of reported methods, discuss general aspects of these test methods for

extrinsic flaws (macrocracks) and intrinsic flaws (microcracks) in test specimens.

Test Methods for R-Curve at Ambient Temperature. Regardless of the organization (ASTM, ISO, CEN, or

JISC), no standardized test method for R-curve behavior of brittle materials has been proposed or approved. In

the future, if the need for such standards are established, it will be useful to build on existing standards for

fracture toughness testing of brittle materials much as ASTM did in developing E 1820.

Direct adaptation of R-curve test methods for metals is one approach that has been successfully used in

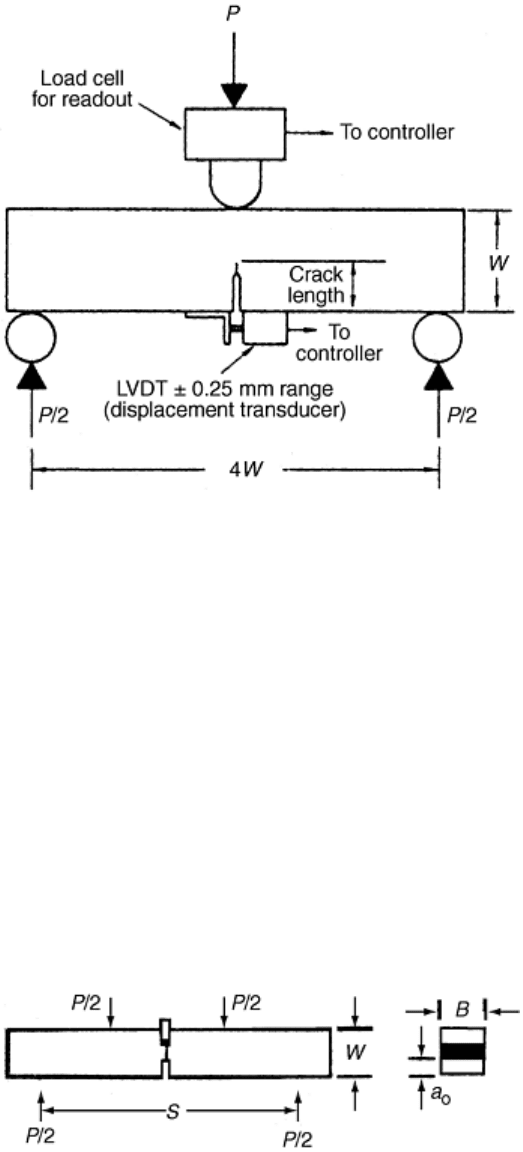
determining the R-curve behavior in brittle materials. As shown in Fig. 17, an SENB test specimen in three-

point flexure was used to test Westerly granite (Ref 39). Single fatigue cracks were introduced at the root of the

notch by cyclic “loading” at 2.2 Hz under crack-mouth displacement (CMD) control mode with an initial force

up to 90% of the breaking force. Both compliance and dye penetration methods were used to determine crack

length during the stable crack-extension part of the fracture test. Apparent fracture toughness (K

) and the J-

integral (J

) as functions of crack length were established.

Fig. 17 Single-edge notch beam (SENB) fracture test specimen of Westerly granite used to determine R-

curve behavior. LVDT, linear variable differential transformer. Source: Ref 39

Using SENB test specimens, but with a slightly different approach for stable crack propagation, the R-curve

behavior of aluminum oxide ceramics was measured (Ref 40). Although no precrack was initiated at the tip of

the notch root, it was reported that the three-point flexure test system was sufficiently stiff to allow stable crack

propagation. Different initial notch depths led to the determination of a notch-depth independent intrinsic

fracture resistance, while a notch-depth dependent fracture resistance as a function of crack length, R(c), was

determined. Both shape and magnitude of the R-curve were dependent on test parameters (i.e., test mode, test

rate, and test specimen geometry).

A variation of the SENB was used to determine the grain-bridging contributions during R-curve testing of

aluminum oxide and magnesium aluminate spinel (Ref 41, 42). A “back-notched” SENB test specimen (Fig.

18) was tested in four-point flexure. An aluminum oxide wedge was inserted into the back notch for load

support throughout the fracture test. The fracture test was conducted until complete propagation of the crack

across the unnotched section of the test specimen. The cracked (but not separated) SENB test specimens were

then longitudinally tested in tension to determine the tensile stress-strain response of the fracture process zone.

The R-curve was inferred from the postfracture tensile test results (Ref 42).

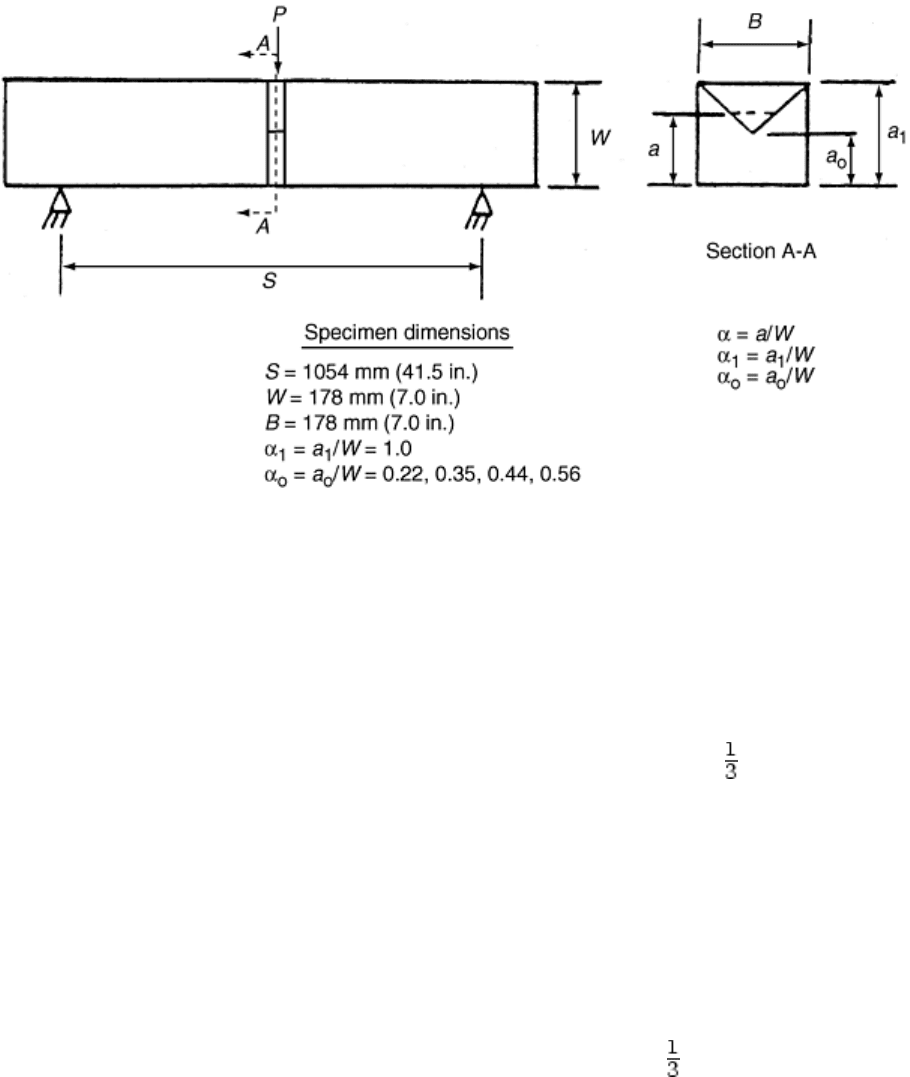
Fig. 18 Single-edge notch beam (SENB) fracture test specimen with back notch and wedge used to

determine R-curve parameters from postfracture tensile tests. Source: Ref 41

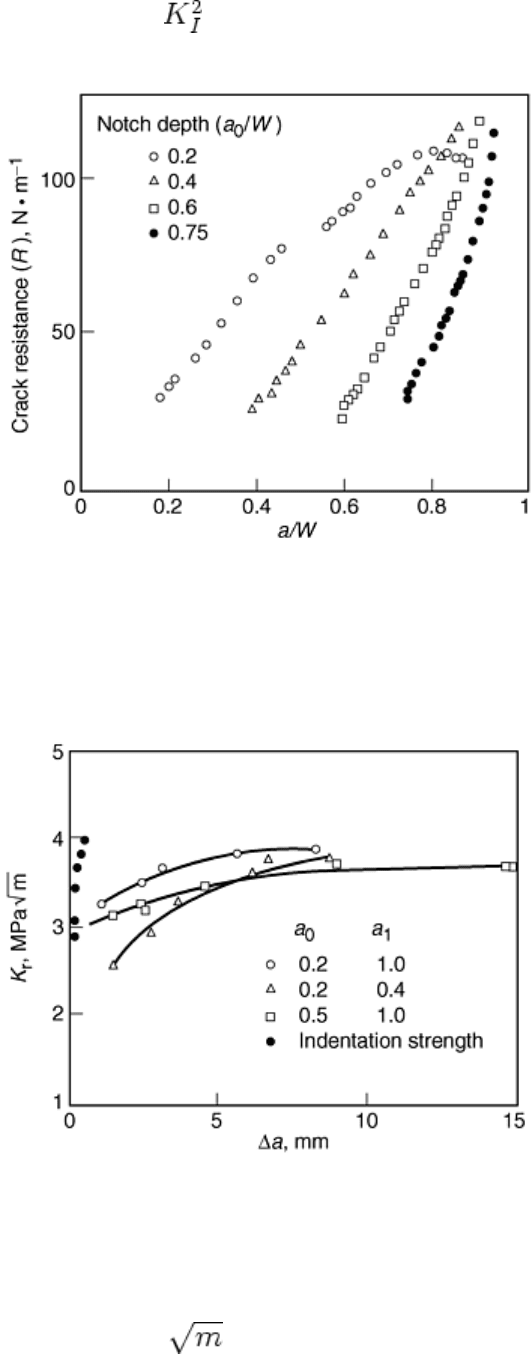
A further study of R-curve effects in aluminum oxide was carried out using CNSB test specimens (Ref 43) (Fig.

12). The inherently stable crack propagation in the chevron notch geometry was used to incrementally extend

the crack before unloading slightly to determine the compliance for calculating the instantaneous crack length.

R-curves were plotted as stress intensity factor versus crack extension. A bearing steel was also evaluated using

this technique (Ref 44).

R -curves for two brittle materials were determined (Ref 45) using one of the test specimen geometries (CNB)

contained in the ASTM standardized fracture toughness method for brittle materials (ASTM C 1421). In this

study, three-point flexure was used with square-cross section test specimens (Fig. 19). The tests were conducted

monotonically, and the instantaneous compliance (not unloading compliance) was used to determine the

instantaneous crack length. Crack mouth opening displacement (CMOD) was measured using a laser

interferometric displacement gage.

Fig. 19 Chevron notched beam (CNB) test specimen in three-point flexure for R-curve effects. Four

normalized depth ratios (α

) were included. Source: Ref 45

R-curve evaluation also was performed using the IS method (Ref 46). When the IS method is used to evaluate

fracture strength/resistance in Eq 17 and 18, fracture toughness is related to the indentation force as well as the

hardness and elastic modulus of the material. This fracture toughness is calculated for each strength test of the

indented flexure test specimens (in these cases, the relationship between the flexural strength, S

, and the

indentation force, P, was assumed to be the theoretical: S

α P-1/3). However, for determining R-curve behavior

and when all the data are fitted [i.e., S

= f(P)], the exponent on P will only be - for materials with flat R-

curves. Furthermore, if the R-curve is described as a power-law function of crack length, the result is (Ref 46):

= k(Δa)

(Eq 25)

where k and τ are constants and Δa is the crack extension, then τ = 0 if the R-curve is flat.

If the R-curve is not flat, then the relationship between flexural strength and indentation force is:

α αP

-β

(Eq 26)

where the exponents β can be defined as τ = (1 - 3β)/(2 + 2β), and the coefficient α is defined as K = Yα(βγ)

-β

+ β)

(1 + β)

where Y and γ are related to the indentation crack geometry. Note that limiting values on τ are 0 for

flat R-curve materials and 0.5 for the steepest rising R-curve material that still fractures catastrophically. This

technique is illustrated in Fig. 20 where the assumption of flat R-curve (β = - ) obviously does not work. Note

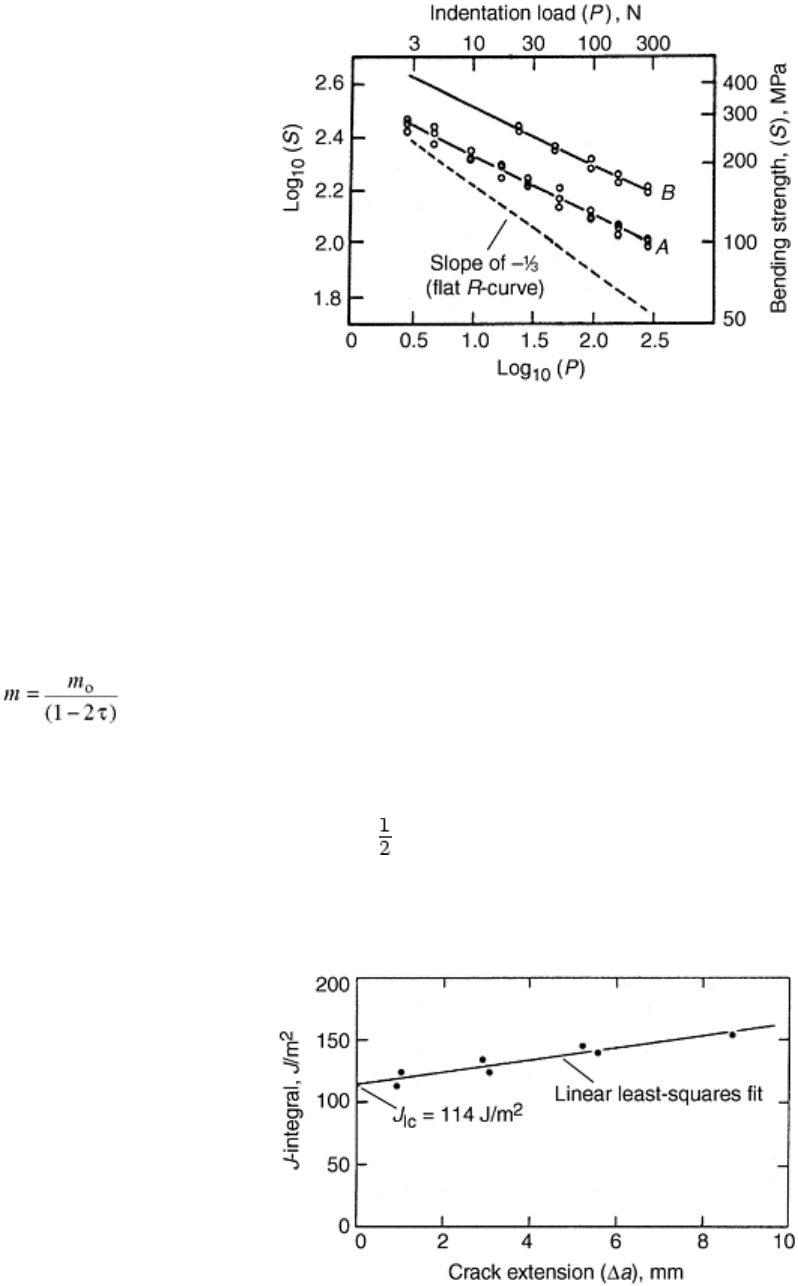
that annealing to relieve the residual stress (A and B in Fig. 20) caused by the deformation of the indenter can

significantly affect the fracture results.

Fig. 20 Indentation strength (IS) fracture test method for R-curve behavior where observed flexural

strength is a function of indentation force in a series of two experiments. Specimens for A included

residual stress of indentation; specimens for B had the residual stress annealed out at elevated

temperature. Source: Ref 46

For design purposes, the utility of this IS fracture test method is not in fracture mechanics-related analyses.

Rather, its greater utility is its application to strength-rated analyses. If the strength distribution is described as

Weibull (weakest link), then the Weibull shape parameter, m (i.e., Weibull modulus), can be related to the

degree of the R-curve by (Ref 47):

(Eq 27)

where m

is the Weibull modulus for τ = 0. Equation 27 holds for a range of flaw sizes related to the

indentations of the IS method. Equation 27 also shows that as the slope of the R-curve increases, so does the

Weibull modulus, thus decreasing the scatter in the strength distribution. Note that m can potentially be equal to

∞ for a deterministic strength (i.e., τ → ).

Examples of R-Curve Test Data. Various types and levels of R-curves exist for brittle materials. For example,

an R-curve for Westerly granite is shown in Fig. 21. Note in this case that the J-integral is plotted as a function

of crack extension. Extrapolation of the R-curves to zero crack extension results in determination of J

, which,

when related to K

, gives an agreement within 4% of K

determined directly (Ref 39).

Fig. 21 J-integral R-curve determined from single-edge notch beam (SENB) fracture test specimens of

Westerly granite. Source: Ref 39

R -curves in terms of an energy parameter ( / E) are plotted in Fig. 22 for an aluminum oxide. Note that

both the slopes and the shapes of the R-curves vary with notch depth, although the initial values of the R-curves

appear to be independent of notch depth (Ref 40).

Fig. 22 R-curves as a function of crack depth for aluminum oxide. Source: Ref 40

R -curves determined from CNSB test specimens and in terms of stress intensity factors are shown in Fig. 23.

Also shown in Fig. 23 is an R-curve determined from the IS method for the same material. Note that the R-

curves are dependent on geometry, test method, and type of crack (intrinsic versus extrinsic) (Ref 44), although

they do band the same K

range.

Fig. 23 Comparison of R-curves for aluminum oxide determined from the chevron notched short bar

(CNSB) and indention strength (IS) methods. Source: Ref 44

With the proper testing configuration, even flat R-curves can be measured using the CNB test specimen, as

shown in Fig. 24 (Ref 45). These R-curves are not only flat, but the fracture toughness for one of the materials

(silicon carbide) is only in the range of 3 MPa .

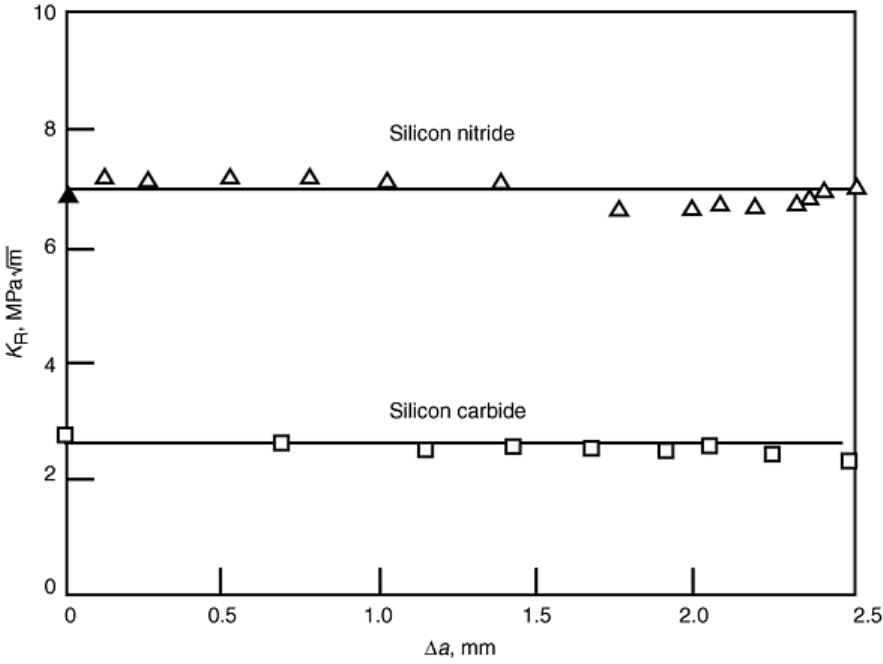
Fig. 24 Flat R-curves for silicon nitride and silicon carbide chevron notched, three-point bend (CNB)

specimens at room temperature. Source: Ref 45

References cited in this section

2. A.A. Griffith, The Phenomena of Rupture and Flow in Solids, Philos. Trans. R. Soc. (London) A, Vol

221, 1920, p 163–198

3. B. Lawn, Fracture of Brittle Solids, Cambridge University Press, 1993

4. K.E. Amin, Toughness, Hardness, and Wear, Ceramics and Glasses, Vol 4, Engineered Materials

Handbook, S.J. Schneider, J., Ed., ASM International, 1991, p 599–609

6. “Standard Test Method for Plane Strain Fracture Toughness of Metallic Materials,” E 399-90, Annual

Book of ASTM Standards, Vol 03.01, ASTM, 1998

7. STP 678, Fracture Mechanics Applied to Brittle Materials, S.W. Freiman, Ed., ASTM, 1979

8. T. Fujii and T. Nose, Evaluation of Fracture Toughness of Ceramic Materials, IJIS Int., Vol 29 (No. 9),

1989, p 717–725

9. G.D. Quinn, M.G. Jenkins, J.A. Salem, and I. Bar-On, Standardization of Fracture Toughness Testing of

Ceramics in the United States, Kor J. Ceram., Vol 4 (No. 4), 1998, p 311–322

10. M. Sakai and R.C. Bradt, Fracture Toughness Testing of Brittle Materials, Int. Mater. Rev., Vol 38 (No.

2), 1993, p 53–58

16. “Standard Test Method for Measurement of Fracture Toughness,” C 1820-96, Annual Book of ASTM

Standards, Vol 3.01, ASTM, 1999