ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

Fig. 14 Two samples of the same material (Al-Cu), one flanged for recovery test and the other unflanged

for data acquisition. Source: Ref 7

The sample is threaded into the transmission bar through the reaction mass R

. The transmission bar rests

against a thin flange F

, constructed in R

by reducing its opening diameter around the sample, as shown in Fig.

12. The other (output) end of the transmission bar is in contact with a bar of the same impedance, which can

trap compression pulses transmitted through the sample into the transmission bar. When the striker hits the

transfer flange of the incident bar, a compression pulse followed by a tension pulse is imparted into the incident

bar, as discussed in the section “Stress-Reversal Technique” in this article. The compression-tension pulse

travels toward the sample and subjects the sample to compression first (which shortens the sample), followed

by tension (which almost restores the initial length of the sample). A part of the compression pulse is

transmitted through the sample into the transmission bar and is trapped at the far end of this bar by the

momentum-trap bar (hatched in Fig. 12). The remaining part of the compression pulse is reflected off the

specimen into the incident bar as tension. This tension then reflects back from the striker end of the incident bar

and returns to the sample as tension because of the presence of the transfer flange, incident tube, and the

reaction mass R

When the tensile segment of the initial compression-tension pulse reaches the specimen, it is partly transmitted

through the sample into the transmission bar and is partly reflected off the sample as compression, back into the

incident bar. As the sample shortens during the compressive loading, prior to the arrival of the tension pulse, its

flange, F

, separates from the reaction mass R

. The subsequent tensile loading (almost) restores the sample's

initial length, bringing the sample's flange (almost) in contact with the reaction mass R

. The tensile pulse,

which reflects as compression from the far end of the transmission bar, returns to the sample, loading it (just

slightly) until the transmission bar comes in contact with the flange F

of the reaction mass R

. At this instant,

the sample flange F

is in complete contact with the reaction mass R

. Shortly after, the tensile pulses, which

are reflected from the loading end of the incident bar, reach the sample, pulling the incident bar away from the

sample, while the sample flange F

is engaged against the reaction mass R

. (As discussed previously, both

compression and tension pulses are reflected as tension from the loading end back into the incident bar.) The

threads that connect the sample to the incident bar are designed to strip off during this final tensile-loading

process. Note that the threads are pulled against the flange F

resting on R

. This prevents loading the sample

over its gage length during this recovery stage. The sample is then recovered, having been subjected to a cycle

of compression-tension loading over its gage length.

The flange F

in combination with the threaded ends of the sample makes the impedance matching difficult

and, hence, complicates the interpretation of the resulting data. This problem can be overcome to a great extent

by performing two tests, one to recover the sample (which has a flange) for post-test analysis and the other

(using a sample that does not have a flange) to collect the required data. Figure 12 shows the two samples. The

corresponding data are given in Fig. 15. Even though the data obtained with the flanged sample are noisy, they

agree quite well with those obtained with the unflanged sample. The unflanged sample, on the other hand, is

subjected to additional tensile pulses, which may cause necking, or even tensile failure of the sample.

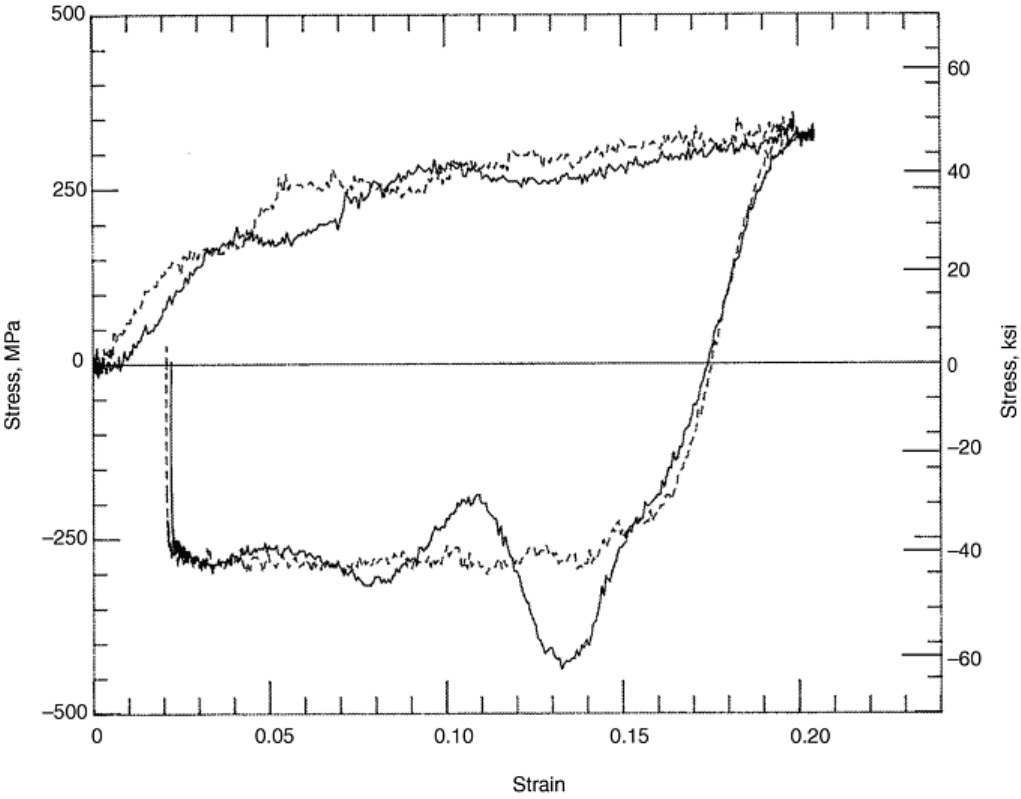
Fig. 15 Data at 3200 s

-1

strain rate, using flanged (solid curve) and unflanged (dashed curve) specimens

(compression is positive). Source: Ref 7

Recovery after Tension and Compression Loading. The recovery tension and compression Hopkinson

techniques can be used to subject a sample to a tensile pulse, recover the sample, produce from it compression

samples (Fig. 16), and then subject these samples to compression and recover them. This allows the studying of

the response and microstructural changes when the material is subjected to a tension, recovered, and then

subjected to a compression (Ref 8, 9). In this approach, the tensile loading is not followed immediately by a

compression pulse. Hence, if there are any microstructural changes during the recovery and preparation of the

compression samples from the original tension sample, these changes may affect the subsequent compression

test results. Indeed, the effects of such changes on the response of the material can be studied by this method.

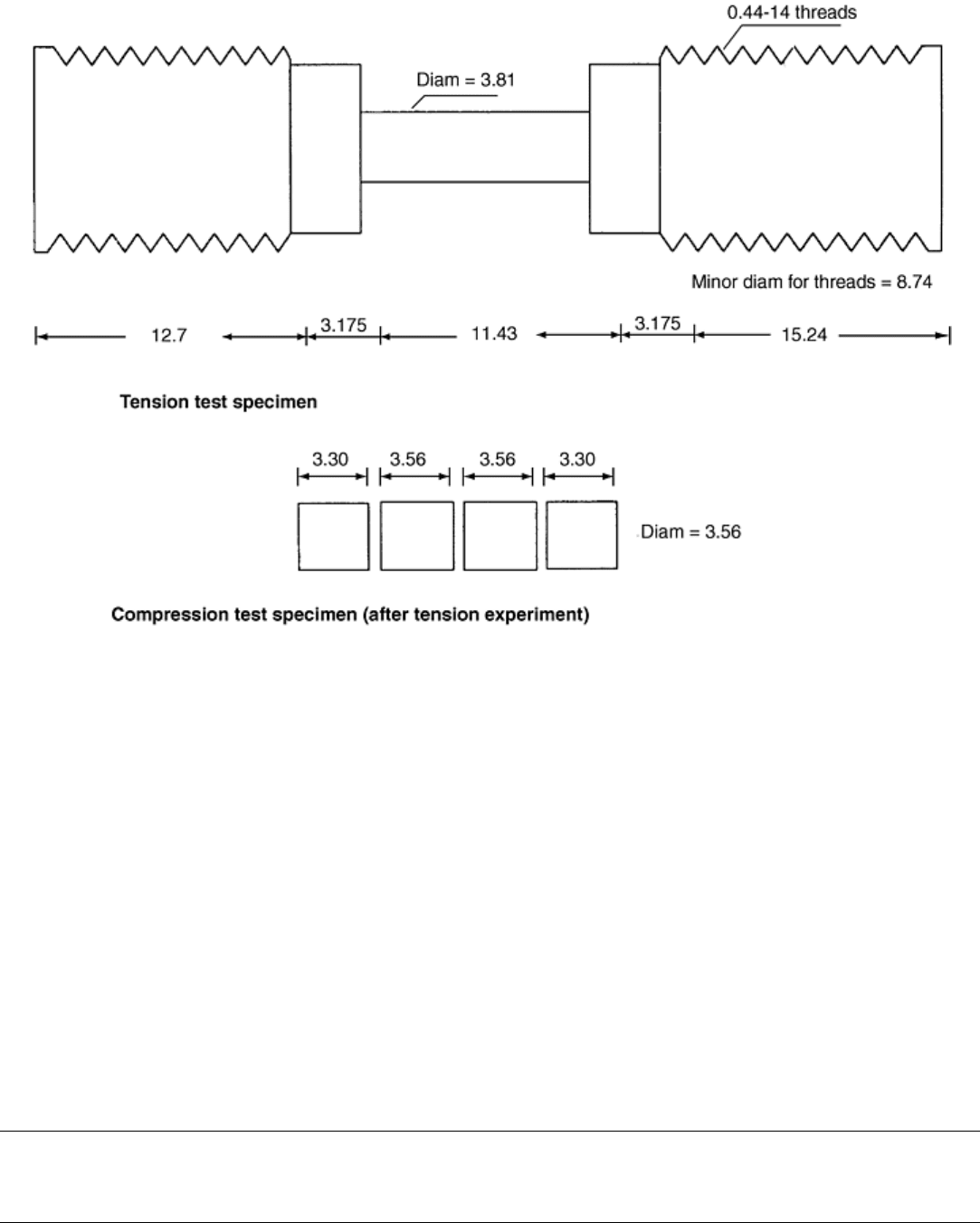
Fig. 16 Sample geometry for high strain rate Bauschinger experiments. Dimensions in millimeters.

Source: Ref 14

References cited in this section

7. S. Nemat-Nasser, J.B. Isaacs, and J.E. Starrett, Hopkinson Techniques for Dynamic Recovery

Experiments, Proc. R. Soc. (London) A, Vol 435, 1991, p 371–391

8. A. Thakur, S. Nemat-Nasser, and K.S. Vecchio, Bauschinger Effect in Haynes 230 Alloy: Influences of

Strain Rate and Temperature, Metall. Mater. Trans., Vol 27A, 1996, p 1739–1748

9. A. Thakur, S. Nemat-Nasser, and K.S. Vecchio, Dynamic Bauschinger Effect, Acta Mater., Vol 44,

1996, p 2797–2807

14. S. Nemat-Nasser, Y Li, and J.B. Isaacs, Experimental/Computational Evaluation of Flow Stress at High

Strain Rates with Application to Adiabatic Shearbanding, Mech. Mater., Vol 17, 1994, p 111–134

Recovery Hopkinson Bar Techniques

Sia Nemat-Nasser, University of California, San Diego

Recovery Dynamic Testing of Hard Materials

Most ceramics are extremely hard and undergo very little strain prior to failing. Their response is essentially

linear, up to failure. Thus, special techniques are necessary in order to perform high strain rate recovery

experiments on these materials.

In the classical compression split-Hopkinson bar, the yield stress of the sample must be considerably smaller

than the yield stress of the bars. The ends of the incident and transmission bars, in contact with the specimen,

therefore remain essentially flat as the sample deforms. Furthermore, the impedance of the sample generally is

considerably smaller than that of the bars throughout the entire loading history. Therefore, the tensile pulse that

reflects off the sample into the incident bar is a good measure of the velocity of the sample end of the incident

bar relative to that of the transmission bar.

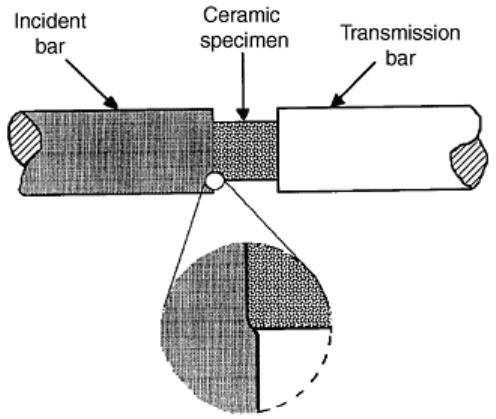
When very hard materials, such as ceramics and ceramic composites, are being tested in the compression split-

Hopkinson bar, the reflected pulse, in general, no longer accurately measures the strain rate in the sample.

Indeed, if the diameter of the sample is not considerably smaller than the diameter of the bar, the impedance of

the sample may be close to, or, in certain cases, even greater than that of the incident bar, resulting in a very

small reflected tensile pulse, or even a reflected compressive pulse. On the other hand, as is often required,

when the diameter of the sample is considerably smaller than that of the bars, the hard sample indents the ends

of the bars (Fig. 17). Furthermore, since the total strain to failure for hard ceramics and their composites is

usually quite small (1 or 2%), the indentation, in general, introduces significant errors in the results if the

reflected pulse is used to calculate the strain in the sample. The reflected wave in the incident bar no longer is

an accurate measure of the strain rate in the sample of hard, brittle materials, although the transmitted pulse is

still a good indication of the stress in the sample.

Fig. 17 Indentation of the bar by a hard (ceramic) specimen. Source: Ref 7

As can be seen from Eq 4, for the sample strain rate to be constant it is necessary that ε

= -(ε

- ε

) be constant.

In the classical Hopkinson technique, this is accomplished by seeking to impart a constant stress pulse into the

incident bar. A constant stress pulse, however, does not produce a constant strain rate in an elastic sample.

Instead, such a pulse deforms the sample in three distinct regimes, namely, an initial regime of positive strain

rate when the stress in the sample increases to a constant level, followed by a regime of zero strain rate, which

is then followed by a regime of negative strain rate. Thus, for hard ceramics, it is necessary to render the strain

differential, ε

- ε

, as nearly constant as possible. This can be achieved by using a ramp pulse.

These basic problems have been solved (Ref 10, 11, 12, 13) using the following techniques:

• The strain is measured directly by attaching strain gages to the sample. For samples with square cross

sections, two strain gages are used, one to measure the axial strain and the other to measure the lateral

strain (Ref 10, 11).

• A thin metal cushion is placed at the striker end of the incident bar to produce a ramp stress pulse in the

incident bar. Figure 18 shows typical stress and strain pulses that can be obtained in this manner. In Ref

7, a detailed analysis of the finite deformation of the copper cushion is given, together with

experimental verification of the results. It is shown that the pulse shape depends on the cushion

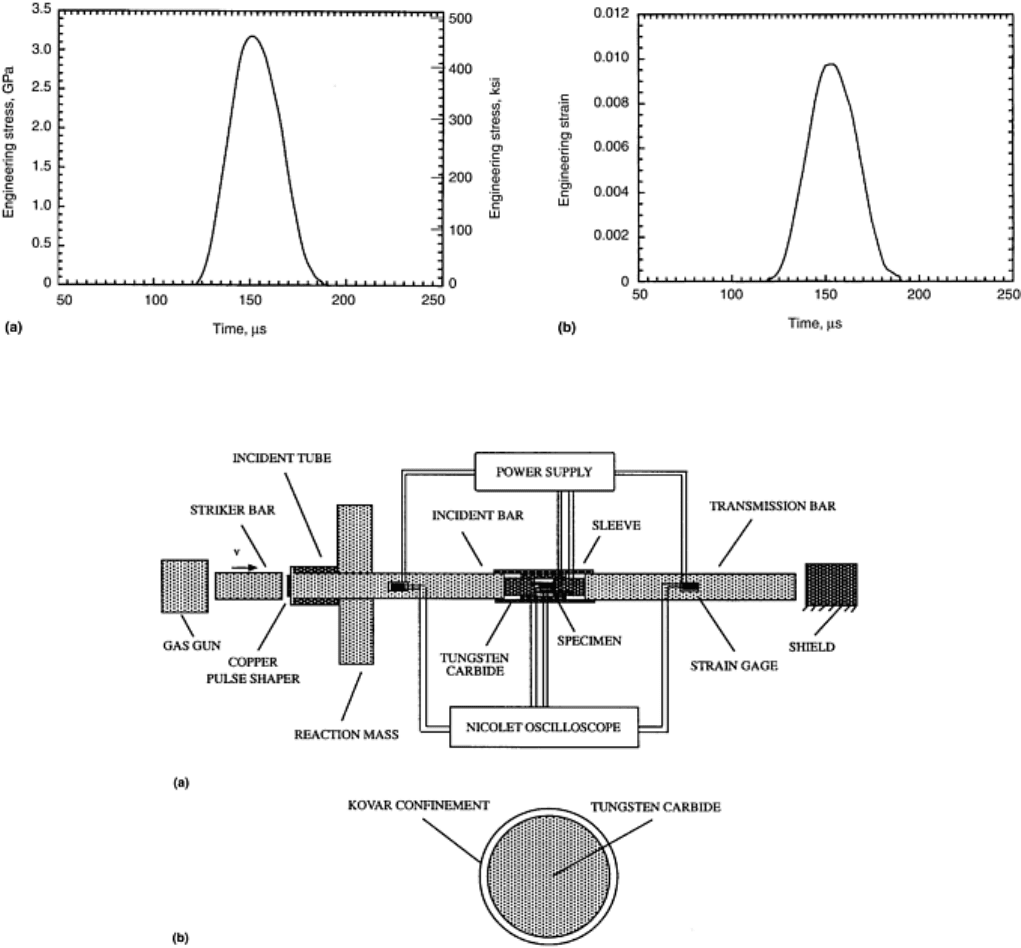
geometry and the length and velocity of the striker and that it can be reliably predicted using finite

plasticity theory.

• The yielding of the bars by the hard ceramic samples can be prevented using an impedance-matched

small platen of polished tungsten carbide. When necessary, a composite of the tungsten carbide, which

is press fitted within a ring of, for example, Kovar, may be used. Figure 19(a) shows the construction

used by Sharma et al. (Ref 12), and Fig. 19(b) shows a composite tungsten-carbide platen. It is

important to attain a good impedance match between the inserts and the bars in such constructions.

Fig. 18 Typical (a) stress and (b) strain pulses obtained by pulse shaping to produce constant strain rate

in an elastic sample. Source: Ref 12

Fig. 19 Modified split-Hopkinson compression bar to test hard ceramics at high strain rates. (a) Test

configuration. (b) Tungsten-carbide platen with Kovar confinement. Source: Ref 12

References cited in this section

7. S. Nemat-Nasser, J.B. Isaacs, and J.E. Starrett, Hopkinson Techniques for Dynamic Recovery

Experiments, Proc. R. Soc. (London) A, Vol 435, 1991, p 371–391

10. W.P. Rogers, J.B. Isaacs, and S. Nemat-Nasser, Effect of Microstructural Damage on Ultrasonic

Velocity and Elastic Moduli of Partially Stabilized Zirconia, Review of Progress in Quantitative

Nondestructive Evaluation, D.B. Thomson and D.E. Chimenti, Ed., Plenum, New York, 1989, p 1827–

1832

11. W.P. Rogers and S. Nemat-Nasser, Transformation Plasticity at High Strain Rate in Magnesia-Partially-

Stabilized Zirconia, J. Am. Ceram. Soc., Vol 73, 1990, p 136–139

12. V. Sharma, S. Nemat-Nasser, and K.S. Vecchio, Dynamic-Compression Fatigue of Hot-Pressed Silicon-

Nitride, Exp. Mech., Dec 1994, p 315–323

13. G. Subhash and S. Nemat-Nasser, Dynamic Stress-Induced Transformation and Texture Formation in

Uniaxial Compression of Zirconia Ceramics, J. Am. Ceram. Soc., Vol 76, 1993, p 153–165

Recovery Hopkinson Bar Techniques

Sia Nemat-Nasser, University of California, San Diego

Applications of Recovery Hopkinson Techniques

The recovery of the sample that has been subjected to a single stress pulse allows a number of interesting

applications, a few of which are reviewed in this section.

Isothermal Flow Stress of Ductile Materials at High Strain Rates. Incremental straining can be used to measure

the strain softening produced by the temperature rise associated with the high strain rate plastic deformation of

ductile samples. The effect of any recovery on the flow stress that may occur during unloading and cooling to

room temperature, and reloading of the sample, is assessed by overlapping the incremental straining of similar

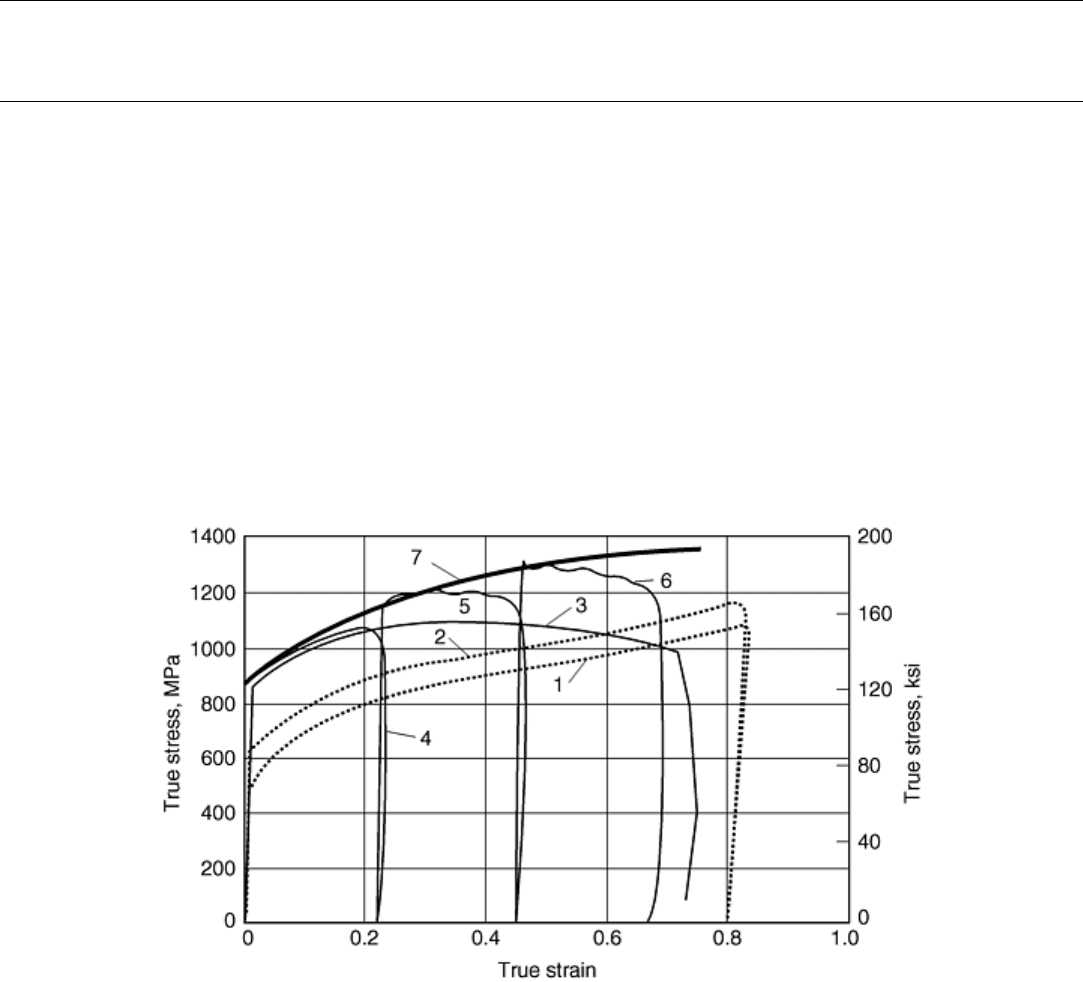
samples of the material. Figure 20 provides results for a tantalum-tungsten alloy (Ta-10%W). Curves 1 and 2

are obtained quasi-statically (Instron machine) at 10

-3

and 1 s

-1

strain rates. Curve 3 is the adiabatic stress-strain

relation at a 5700 s

-1

strain rate, starting with 25 °C (77 °F) initial temperature; different samples are used. To

obtain the (quasi-) isothermal flow stress at a 5700 s

-1

strain rate, a fourth sample is deformed incrementally in

the recovery Hopkinson system, obtaining curves 4, 5, and 6. Then, curve 7 is constructed using these results.

Fig. 20 The true stress-true strain relations for Ta-10%W at 25 °C (77 °F). Curves 1, 2, and 7 are

isothermal relations at strain rates of 10

-3

, 1, and 5700 s

-1

. Curve 5 is adiabatic at 5700 s

-1

strain rate.

Source: Ref 1

Before accepting curve 7 as the quasi-isothermal stress-strain relation of this material, it is necessary to

establish whether a uniform stress state is attained in the sample prior to yielding in each straining increment.

The sample in this experiment was 3.8 mm (0.15 in.) long. The duration of the elastic wave to travel the length

of the sample is about 1.2 μs. Hence, the stress in the sample is essentially uniform after 5 μs. The time required

to bring the sample to its yield point is greater than 10 μs. Hence, a uniform stress is attained in each

incremental loading prior to yielding.

The results in Fig. 20 also show that the differences among curves 1, 2, and 7 are only due to the change in the

strain rate because the effect of temperature is now removed. It is interesting to note that these three curves are

essentially parallel, their common slope being a measure of the material's work hardening. Moreover, the

thermal softening can be read off directly from the difference between curves 3 and 7.

It is also possible to check whether there have been any substantial changes in the microstructure of the

material, when the sample is unloaded and cooled to room temperature, in each incremental loading. In

addition, it is possible to evaluate the part of the plastic work, which is used to increase the sample temperature

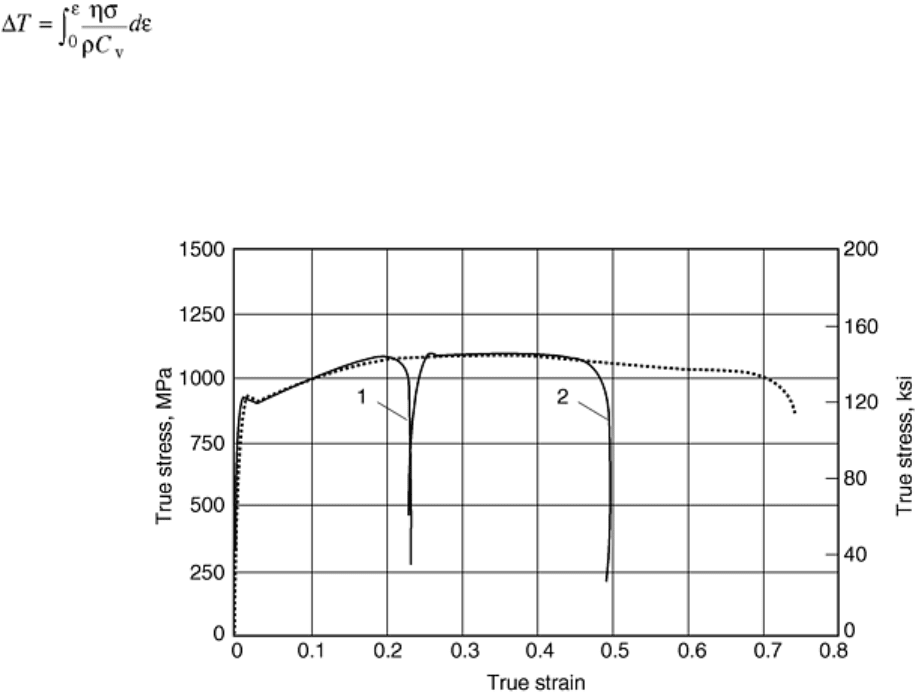
during its high strain rate deformation. This is illustrated by the results given in Fig. 21 for the same Ta-10% W

alloy, tested at the same 5700 s

-1

strain rate. The dashed curve in this figure is the adiabatic result. Curve 1 is

obtained by an incremental deformation of a new sample of the same material, at the same strain rate, in the

recovery Hopkinson system. It follows the dashed curve closely, indicating the repeatability of the experiment.

The area under this solid curve can be used to calculate the total plastic work per unit mass. The change in the

temperature of the sample can then be computed from:

(Eq 10)

where ε and σ are the axial strain and stress in the sample, respectively; ρ is the mass density of the sample; and

is the (temperature-dependent) heat capacity at constant volume. In Eq 10, η is the fraction of the energy

used to increase the sample temperature. To obtain curve 2 in Fig. 21, it was necessary to assume that all the

plastic work was used to increase the sample temperature, setting η = 1. The results show that, to within

experimental errors, this is a good assumption for the present case (see Ref 15 for comments and comparison

with infrared measurements using several different materials).

Fig. 21 The true stress-true strain relations for Ta-10%W at 5700 s

-1

strain rate; all three curves are

adiabatic, with an initial temperature of 25 °C (77 °F) for the dashed curve and for curve 1 and an initial

temperature of 135 °C (275 °F) for curve 3. Source: Ref 1

References cited in this section

1. S. Nemat-Nasser and J.B. Isaacs, Direct Measurement of Isothermal Flow Stress of Metals at Elevated

Temperatures and High Strain Rates with Application to Ta and Ta-W Alloys, Acta Metall., Vol 45,

1997, p 907–919

15. R. Kapoor and S. Nemat-Nasser, Determination of Temperature Rise during High Strain Rate

Deformation, Mech. Mater., Vol 27, 1998, p 1–12

Recovery Hopkinson Bar Techniques

Sia Nemat-Nasser, University of California, San Diego

High-Temperature Dynamic Recovery Tests

For high strain rate tests at elevated temperatures, it is necessary to heat the sample to the required temperature

while keeping the incident and transmission bars at suitably low temperatures. If the bars are in contact with the

specimen within the furnace, their temperature will increase, having a variable distribution along the bars. This

affects the elastic properties of the bars and, hence, the stress pulses. Moreover, the bars being good heat

conductors (usually of maraging steel), the considerable heat loss that occurs makes controlling the experiment

difficult.

Different techniques are required in order to alleviate these difficulties when testing metals that are ductile and

ceramics that are hard and brittle, as discussed subsequently.

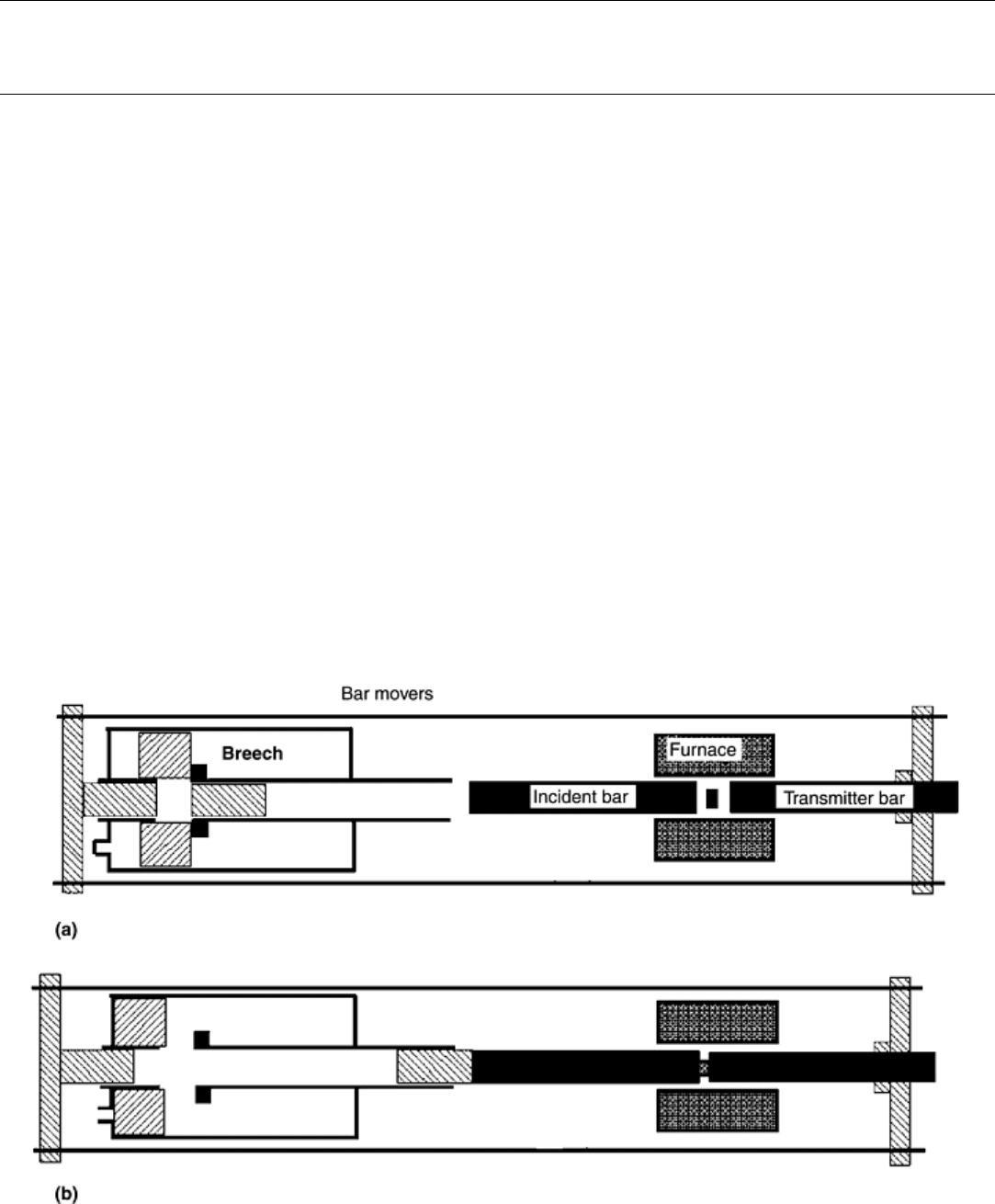
High-Temperature, High Strain Rate Testing of Ductile Materials. In this case, the bars are kept outside the

range of the heating unit in the furnace, while keeping the specimen at the center of the furnace. The bars are

then brought into contact with the specimen microseconds before the stress pulse reaches the end of the incident

bar. This is accomplished by two bar movers that are activated by the same gas gun that propels the striker bar

toward the incident bar. Figure 22(a) illustrates the experimental setup just before the gun is fired, and Fig.

22(b) shows the configuration after the bar movers have brought the incident and transmission bars in contact

with the sample. The motion of the bar movers is controlled by the area of its piston and the gas pressure in the

breech of the gas gun. In a properly designed system of this kind (Ref 1), the bars are brought into contact with

the specimen microseconds before the sample is loaded by the elastic pulse traveling in the incident bar. Once

the sample is loaded, the bars move out, and the sample is recovered without having been subjected to any

stresses other than the initial one.

Fig. 22 Operation of the high-temperature recovery Hopkinson bar (a) before and (b) during the test.

Source: Ref 1

Figure 23(a) shows the furnace and the ends of the incident and transmission bars. Figure 23(b) shows the

relative position of the sample held by thermocouples, and the ends of the incident and transmission bars; this is

the configuration maintained in the furnace just before firing the gas gun. The sample is attached by suitable

wires to a sleeve, which is a thin tube. The bar movers then move the transmission bar, bring it into contact with

the sample, and then the sample, the sleeve, and the transmission bar are brought into contact with the incident

bar. Figure 23(c) shows the furnace and the sample attached to the sleeve outside of the furnace. Figure 23(d)

shows the bar movers attached to the breech of the gas gun of the Hopkinson construction.

Fig. 23 Dynamic recovery testing at high temperatures. (a) Furnace over the end of the incident and

transmission bars. (b) Position of the sample when held by thermocouples. (c) Furnace and the sample

attached to the sleeve. (d) Bar movers attached to the breech of the gas gun of the Hopkinson

construction. Source: Ref 1

Isothermal Flow Stress of Ductile Materials at High Temperatures and High Strain Rates. To produce an

isothermal flow stress at a high strain rate and high temperature, the sample is heated to the required

temperature in the furnace attached to the recovery Hopkinson bar and then loaded incrementally. After the

application of each load increment, the sample is unloaded without being subjected to any additional stress

pulses. The sample is then allowed to return to room temperature, its dimensions are measured, and it is

reheated in the furnace to its initial temperature before the application of the next strain increment.

Since the unloading, the cooling of the sample, the reheating to its initial temperature, and the reloading may

affect the microstructure and, hence, the thermomechanical properties of the material, it is necessary to check

this in each case. To this end, a sample that has been loaded, unloaded, and cooled to its initial temperature may

then be reheated to the temperature it had reached just prior to its unloading. If there are no substantial changes

in the microstructure that affect the flow-stress properties, then the flow stress, upon reloading, should follow

the previous stress-strain curve. The procedure is similar to that described for Fig. 21. The only difference is the

initial temperature.

As an application, consider measurement of the high strain-rate isothermal flow stress of the Ta-10%W alloy at

325 °C (615 °F); see Fig. 24. The room-temperature results are the same as in Fig. 20. Figure 24 includes the

high strain rate, room-temperature results reported in Fig. 20; for example, curve 3 in Fig. 24 is the same as

curve 7 of Fig. 20.

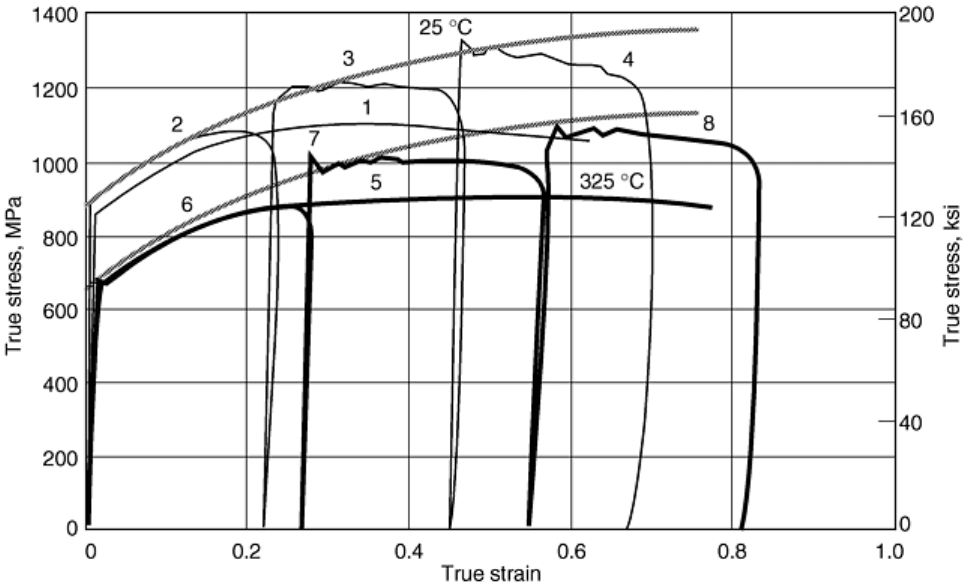
Fig. 24 True stress-true strain relations for Ta-10%W at 5700 s

-1

strain rate. Curves 1, 2, 3, and 4 are for

25 °C (77 °F), and curves 5, 6, 7, and 8 are for 325 °C (615 °F) initial temperatures. The isothermal

curves for 25 °C (77 °F) and 325 °C (615 °F) are essentially parallel.

With an approach similar to that for the room-temperature tests of Fig. 20, but now using an attached furnace,

the results given in Fig. 24 for a 325 °C (615 °F) initial temperature have been obtained. As is seen, the quasi-

isothermal curves for 25 and 325 °C (77 and 615 °F) initial temperatures are almost parallel, showing

essentially the same work hardening for the Ta-10%W alloy. Comparing these results with those of Fig. 24, it is

seen that the isothermal work hardening seems to be independent of the temperature for this material, within the

considered temperature and strain rate ranges. Hence, the work hardening due to plastic straining is not coupled

with either temperature or strain rate. This is an important property since the flow stress then can be divided

into an athermal part and a thermally activated part where the athermal part may be assumed to depend solely

on the microstructure. The thermal part is due to the short-range barriers to the motion of dislocations (Ref 16).

Note that here again it is necessary to establish whether a uniform stress state is attained in the sample, prior to

yielding in each incremental straining, and whether the structure of the material is affected by the cycle of

unloading, cooling, reheating, and reloading, as discussed in the section “Isothermal Flow Stress of Ductile

Materials at High Strain Rates.”

High-temperature, high strain rate testing of hard, brittle materials poses the following challenges:

• It is necessary to prevent the indentation of the bars by the sample.

• It is necessary to heat the sample while keeping the bars outside the heating zone within the furnace.

• It is necessary to measure the strain of the sample at high temperatures within the furnace.

In compression, these qualifications can be met as follows. First, in addition to the techniques outlined in the

section “Recovery Dynamic Testing of Hard Materials,” long inserts (e.g., 1 in.) are used for elevated-

temperature tests. The use of longer inserts ensures that while the sample is heated to the required temperature,

the bars remain at a suitably low temperature. Second, since strain gages have a limited temperature range of

operation and cannot be used at elevated temperatures, differential strain measurement (DSM) has been

developed to obtain accurate and reliable measurements of strains for dynamic tests of hard ceramics at

elevated temperatures.

The DSM technique is based on the observation that an error is introduced due to the presence of the inserts and

their interfaces with the sample and the bars. Hence, the displacement recorded by the strain gage on the