ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation
Подождите немного. Документ загружается.


The 1- and 2-wave analyses used to calculate average stress discussed in the theory section implicitly assume
that the strain-time pulses measured at the strain gages are identical with those at the ends of the bars in contact
with the specimen. This assumption, however, is not correct because the specimen is normally smaller in
diameter than the bar such that the bar ends are not uniformly loaded across their diameter and, therefore, will
indent elastically. In addition, as the bars are compressed longitudinally, albeit elastically, they expand radially
in response to the applied force (i.e., the Poisson effect). While the exact mathematical descriptions of these
effects on the propagation of an elastic pulse through a large elastic rod are very complex, the result is that
different frequencies of pulses induced in the bars disperse with distance traveled in the bar. The result of this
dispersion is such that the pulse induced in the input bar through the impact of the striker bar does not
immediately rise into a steady square-wave impulse of fixed amplitude but rather “rings” up. These end effects
quickly dampen after the wave has propagated about ten bar diameters (Ref 40, 67).
The wave propagation behavior thereafter becomes fully described by the equation of motion in an infinite
cylindrical solid. The solution of the equation of motion for these boundary conditions was derived
independently during the late 19th century by the mathematicians Pochhammer (Ref 70) and Chree (Ref 71).
These relations were later specifically applied to address dispersion in the SHPB (Ref 12, 15, 40, 72, 73, 74).
The pressure bars have been determined to vibrate predominantly in a fundamental mode (i.e., while there are
an infinite number of potential solutions to the equation of motion according to the vibrational mode, only one
frequency appears to dominate in long elastic bars).
This vibration of the bar leads to wave dispersion that can mask resolution of the fine details in the stress-strain
data of interest, particularly at higher strain rates where the period of the oscillations can be a large fraction of
the total strain measured. While this elastic dispersion cannot be eliminated, techniques have been adopted
based on the Pochhammer-Chree equation of motion to correct for any additional dispersion that occurs during
the wave propagation from the specimen/bar interfaces to the gage locations (Ref 40, 72, 74, 75, 76, 77).
At any position, z, along the pressure bar, the wave, f(t), may be represented by an infinite cosine Fourier series:
(Eq 20)
where ω
0
is the frequency of the longest wavelength component (n = 1), and δ
n
is the phase angle of component
nω
0
. The wave dispersion in the pressure bars occurs because higher-frequency components travel more slowly
than lower-frequency components and thus lag behind the leading edge of the wave. The dispersion results in a
change of relative position and amplitude of the oscillations, together with a gradual increase in the rise time of
the pulse as it travels along the bar. Because the strains measured in the pressure bars are measured by strain
gages located some distance from the specimen, the pulse shapes at the strain-gage positions will be modified
because of the dispersion effects and therefore do not accurately represent the pulse shapes at the specimen
location.
The dispersion of the waves alters the phase angle, δ, such that at a position, z + Δz, the new phase angle can be
calculated:
(Eq 21)
where C
0
is the longitudinal wave speed in the bar, and C
n
is the velocity of component nω
0
. The value of C
n
depends on the wavelength and on the mode of vibration; in the SHPB case, this is dominated by the
fundamental mode (Ref 12). The phase angle at any position along the bar can be calculated using Eq 21, and
the wave reconstructed at that new position using Eq 20. Accordingly, the raw stress-versus-strain data
calculated using either the 1- or 2-wave analysis can be dispersion corrected by mathematically moving the
wave to a common point on the bar (e.g., the bar-sample interface). This correction removes a large amount of
the inherent wave dispersion, thereby yielding smoother final stress-strain curves (Ref 40, 43, 55, 72, 73, 78,
79).
Direct-Impact Compression Hopkinson Pressure Bar. Several researchers have suggested that one way to avoid
the dispersion problem in the incident bar is to dispense with the incident bar altogether and impact the sample
directly with the striker bar (Ref 72, 80 81 82 83 84 85 86 87 88). The initial intent of the direct-impact bar was
to be used as a means of increasing the maximum strain rate achievable. While maximum higher strain rates
can, in principle, be achieved using this technique, direct Hopkinson bars pose several difficulties. The first
difficulty is that, because there is no incident bar, there is no means to calculate the strain rate and thereby the
strain. Direct strain measurement on the sample and/or high-speed photography must be used to track diametral
sample expansion and therefore the strain. Careful study has shown that this is problematic, but this limitation
can be overcome (Ref 83, 89). The second problem is that it is more difficult to achieve a constant strain rate in
the sample because the direct impact of the striker bar on the sample lacks the equilibrium pulse achieved
during the ringup in the incident bar in the split-Hopkinson configuration.
References cited in this section
3. P.S. Follansbee, The Hopkinson Bar, Mechanical Testing, Vol 8, ASM Handbook, American Society for
Metals, 1985, p 198–203
12. R.M. Davies, A Critical Study of the Hopkinson Pressure Bar, Philos. Trans. R. Soc. (London) A, Vol
240, 1948, p 375–457
15. H. Kolsky, Stress Waves in Solids, J. Sound Vib., Vol 1, 1964, p 88–110
18. G.T. Gray III, High-Strain-Rate Testing of Materials: The Split-Hopkinson Pressure Bar, Methods in
Materials Research, E. Kaufmann, Ed., John Wiley Press, 1999, in press
40. P.S. Follansbee and C. Frantz, Wave Propagation in the SHPB, J. Eng. Mater. Technol. (Trans. ASME),
Vol 105, 1983, p 61–66
43. C.E. Frantz, P.S. Follansbee, and W.T. Wright, Experimental Techniques with the SHPB, High Energy
Rate Fabrication—1984, I. Berman and J.W. Schroeder, Ed., American Society of Mechanical
Engineers, 1984, p 229–236
55. C. Bacon, Numerical Prediction of the Propagation of Elastic Waves in Longitudinally Impacted Rods:
Applications to Hopkinson Testing, Int. J. Impact Eng., Vol 13, 1993, p 527–539
67. J. Yuan, N. Takeda, and A.M. Waas, A Note on Data Processing in the Split Hopkinson Pressure Bar
Tests, Exp. Tech., Vol 1, 1998, p 21–24
70. L. Pochhammer, About the Initiation of the Velocities of Small Oscillations in Unbounded Isotropic
Circular Cylinders, J. Reine Angew. Math., Vol 81, 1876, p 324–336 (in German)
71. C. Chree, The Equations of an Isotropic Elastic Solid in Polar and Cylindrical Coordinates: Their
Solution and Application, Trans. Camb. Philos. Soc., Vol 14, 1889, p 250–369
72. D.A. Gorham, Measurement of Stress-Strain Properties of Strong Metals at Very High Strain Rates,
Inst. Phys. Conf. Series, Vol 47, 1980, p 16–24
73. J.C. Gong, L.E. Malvern, and D.A. Jenkins, Dispersion Investigation in the Split Hopkinson Pressure
Bar, J. Eng. Mater. Technol. (Trans. ASME), Vol 112, 1990, p 309–314
74. C. Bacon, An Experimental Method for Considering Dispersion and Attenuation in a Viscoelastic
Hopkinson Bar, Exp. Mech., Vol 38, 1998, p 242–249
75. C.K.B. Lee, R.C. Crawford, K.A. Mann, P. Coleman, and C. Petersen, Evidence of Higher
Pochhammer-Chree Modes in an Unsplit Hopkinson Bar, Meas. Sci. Technol., Vol 6, 1995, 853–859
76. C.K.B. Lee and R.C. Crawford, A New Method for Analyzing Dispersed Bar Gauge Data, Meas. Sci.
Technol., Vol 4, 1993, p 931–937
77. D.A. Gorham, A Numerical Method for the Correction of Dispersion in Pressure Bar Signals, J. Phys.
E, Vol 16, 1983, p 477–479

78. G. Gary, J.R. Klepaczko, and H. Zhao, Corrections for Wave Dispersion and Analysis of Small Strains
with Split Hopkinson Bar, J. Phys. (France) IV Colloq., C3 (DYMAT 91), Vol 1, 1991, p 403–410 (in
French)
79. D.A. Gorham and X.J. Wu, An Empirical Method for Correcting Dispersion in Pressure Bar
Measurements of Impact Stress, Meas. Sci. Technol., Vol 7, 1996, p 1227–1232
80. C.K.H. Dharan and F.E. Hauser, Determination of Stress-Strain Characteristics at Very High Strain
Rates, Exp. Mech., Vol 10, 1970, p 370–376
81. A.L. Wingrove, A Device for Measuring Strain-Time Relationships in Compression at Quasi-Static and
Dynamic Strain Rates, J. Phys E, Sci. Instrum., Vol 4, 1971, p 873–875
82. G.L. Wulf and G.T. Richardson, The Measurement of Dynamic Stress-Strain Relationships at Very
High Strain Rates, J. Phys. E, Vol 7, 1974, p 167–169
83. D.A. Gorham, P.H. Pope, and J.E. Field, An Improved Method for Compressive Stress-Strain
Measurements at Very High Strain Rates, Proc. R. Soc. (London) A, Vol 438, 1992, p 153–170
84. C.W. Fong, Crack Initiation in Perforated Propellants under High Strain Rate Impact Conditions,
Propell. Explos. Pyrotech., Vol 10, 1985, p 91–96
85. S.M. Walley, J.E. Field, and S.J.P. Palmer, Impact Sensitivity of Propellants, Proc. R. Soc. (London) A,
Vol 438, 1992, p 571–583
86. S.Y. Ho, High Strain Rate Impact Studies of Predamaged Rocket Propellants, Part I: Characterization of
Damage Using a Cumulative Damage Criterion, Combustion & Flame, Vol 104, 1996, p 524–534
87. S.M. Walley, J.E. Field, P.H. Pope, and N.A. Safford, A Study of the Rapid Deformation Behaviour of a
Range of Polymers, Philos. Trans. R. Soc. (London) A, Vol 328, 1989, p 1–33
88. O.S. Lee, S.S. You, J.H. Chong, and H.S. Kang, Dynamic Deformation under a Modified Split
Hopkinson Pressure Bar Experiment, KSME Int. Journal, Vol 12, 1998, p 1143–1149
89. P.H. Pope and J.E. Field, Determination of Strain in a Dynamic Compression Test, J. Phys. E, Sci.
Instrum., Vol 17, 1984, p 817–820
Classic Split-Hopkinson Pressure Bar Testing
George T. (Rusty) Gray III, Los Alamos National Laboratory
Sample Design and Preparation
The errors due to radial and longitudinal inertia as well as friction effects can be reduced by choosing a sample
size that minimizes the areal mismatch between the sample and the bar diameter and maintains a sample L/D
ratio of 0.5 to 1.0.
For a given bar diameter, the sample diameter is typically chosen to be ~80% of the bar diameter for a
compression bar test. Such a ratio allows ~30% true strain to be imparted into the sample before the sample
exceeds the bar diameter. Samples for compressive split-Hopkinson bar testing similar to conventional low-rate
compression testing need to be machined such that the two loading faces are flat, parallel to a 0.001 in. (0.01

mm) tolerance or better, as well as having the sides of the sample orthogonal to the loading faces. For brittle
materials, this tolerance must be an order of magnitude greater. Orthogonality, as well as precision machining
of parallel flat loading faces, is crucial to attaining uniform elastic loading in a compressive Hopkinson bar test
and thereafter achieving a uniform stress-state in the sample.
While most investigators using the split-Hopkinson bar routinely use right-regular cylindrical samples, cubes
and other square-sided shapes can be used. Ease of machining on a lathe to achieve accurate and reproducible
sample specifications also favors cylindrical samples. The selection of the optimal sample diameter and L/D
ratio is dependent on the maximum strain rate desired as well as the sample size requirement necessary to have
specimens sufficiently large to ensure measurement of bulk properties of the material of interest. Coarse-scaled
microstructures or composite materials require larger sample sizes than fine-scaled ones. An approximate rule
of thumb is that the specimen diameter needs to be at least ten times the representative microstructural unit size
for polycrystalline metals and alloys. Coarse-scaled materials, particularly, engineering composites such as
concrete (Ref 90) or polymeric layups, require careful sample-size selection as well as specifically designed
split-Hopkinson bars to achieve valid high-strain-rate stress-strain data.
Sample designs for Hopkinson bar testing of materials exhibiting a low resistance to axial cracking, such as
ceramics, and/or composite matrix/reinforcement debonding, require the use of specialized sample designs. The
use of “dog-bone” samples, originally designed by Tracy (Ref 91), allow the achievement of stable uniaxial
stress in ceramics during Hopkinson bar testing. By suppressing axial cracking and/or brittle fracture processes
in ceramic or cermet samples, because of the larger diameter ends of the samples, valid Hopkinson bar tests can
be achieved (Ref 92). Accurate measurement of the high-strain-rate mechanical behavior of fiber-reinforced
composite samples also requires a specialized sample design. Uniaxial testing of composites can be achieved
using tapered compression samples with end sections constrained with chamfered rings to suppress axial
splitting (Ref 93).
References cited in this section
90. C. Albertini, E. Cadoni, and K. Labibes, Dynamic Mechanical Behaviour of Large Concrete Specimens
by Means of a Hopkinson Bar Bundle, Proc. 2nd Int. Symp. on Impact Eng., C.Y. Chiem, L.L. Wang,
and S. Tanimura, Ed., Chinese Journal of Mechanics Press, Beijing, 1996, p 214–219
91. C.A. Tracy, A Compression Test for High Strength Ceramics, J. Test. Eval., Vol 15, 1987, p 14–19
92. W.R. Blumenthal and G.T. Gray III, Characterization of Shock-Loaded Aluminum-Infiltrated Boron
Carbide Cermets, S.C. Schmidt, J.N. Johnson, and L.W. Davison, Ed., North-Holland Press, 1990, p
393–396
93. H. Couque, C. Albertini, and J. Lankford, Failure Mechanisms in a Unidirectional Fire-Reinforced
Thermoplastic Composite under Uniaxial, In-Plane Biaxial and Hydrostatically Confined Compression,
J. Mater. Sci. Lett., Vol 12, 1993, p 1953–1957
Classic Split-Hopkinson Pressure Bar Testing
George T. (Rusty) Gray III, Los Alamos National Laboratory
High-Rate Uniaxial Stress-Loading Effects on Materials
High-rate testing is conducted on a large number of materials of scientific and engineering interest to support
the development of materials constitutive models (Ref 46, 94, 95, 96, 97, 98). Figure 9 shows the stress-strain
response of electrical-grade iron measured in compression at various strain rates and temperatures. The range of
temperatures and strain rates is conducted to facilitate a robust constitutive modeling fit for this metal. The
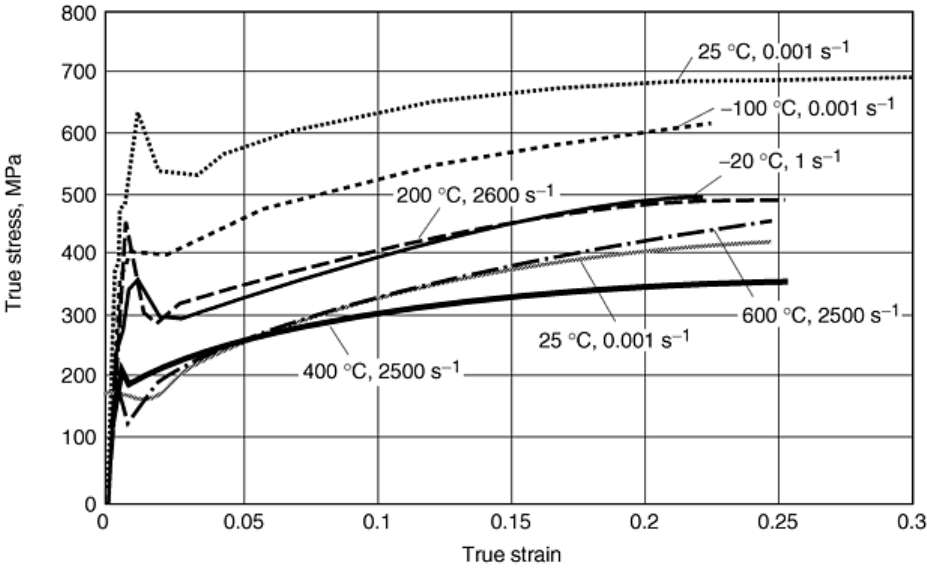
lower strain-rate tests were performed on a standard screw-driven Instron testing machine using the same
specimen geometry as the dynamic tests. All the stress-strain curves, as a function of temperature and strain
rate, are true values. Although the SHPB data at strains below ~1 to 2% are not in stress-state equilibrium, the
curves are plotted in their entirety from load inception. Increasing strain rate at ambient temperature, 298 K, is
seen to increase the flow stress of iron (Fe) equivalent to a decrease in temperature at a constant strain rate.
Fig. 9 Stress-strain response of electrical iron as a function of strain rate and temperature
The response of the iron in Fig. 9 is similar to that of other body-centered-cubic (bcc) metals and alloys, such as
tantalum (Ta), tungsten (W), molybdenum (Mo), and niobium (Nb) (Ref 94) and hexagonal-close-packed (hcp)
metals and alloys, such as zirconium (Zr), beryllium (Be), zinc (Zn), and titanium (Ti) (Ref 99, 100). In this
class of metals, strain-hardening responses after yielding are nearly invariant as a function of strain rate (i.e.,
the stress-strain curves are all nearly parallel in slope although offset in their initial yields). This response is
typical of bcc, hcp, and lower-symmetry metals where the Peierls stress dominates low-temperature and high-
strain-rate mechanical behavior (Ref 94).
Other materials, including high-purity, face-centered cubic metals in an annealed condition, such as copper
(Cu), nickel (Ni), aluminum (Al), and silver (Ag), conversely exhibit nearly strain-rate independent yielding
behavior while their post-yield strain hardening is strongly rate dependent. The stress-strain behavior of high-
purity silver given in Fig. 10 is typical of this class of materials. Indepth knowledge of the simultaneous
influence of temperature and strain rate is used as the basis for advanced materials model development to
describe high-strain-rate material response.
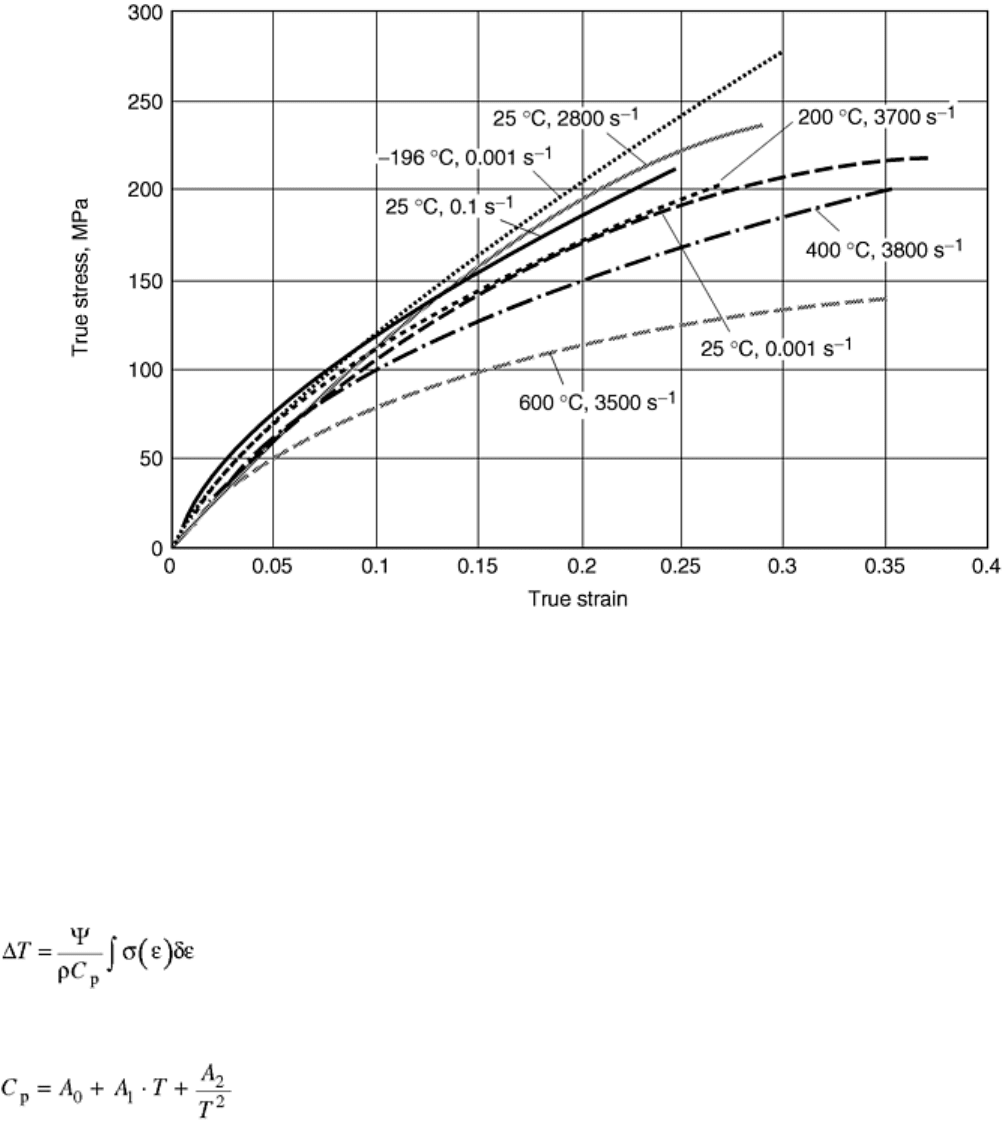
Fig. 10 Stress-strain response of high-purity silver as a function of strain rate and temperature
In addition to the direct influence of strain rate on stress-strain behavior by modifying defect generation and
storage processes, high-rate deformation also alters the measured mechanical response due to the adiabatic
heating accompanying high-rate plastic deformation. While adiabatic heating can be neglected during
quasistatic deformation, the effect of adiabatic heating on the measured high-rate stress-strain behavior of
materials must be considered. To extract an isothermal curve of the material response at a high rate, a
relationship between temperature and stress must be assumed, and the data corrected accordingly. The
temperature increase, ΔT, for mechanical tests at strain rates above 500 s
-1
can be calculated assuming a certain
percentage, Ψ of the work of plastic deformation is converted into heat (Ref 101, 102):
(Eq 22)
where σ and ε are the true stress and strain, respectively; ρ is the density; and C
p
is the heat capacity that can be
written in the form (Ref 103):
(Eq 23)
Adiabatic heating may be significant in samples deformed at high strain rates, particularly at higher strains.
Careful consideration of adiabatic effects on overall constitutive response is crucial to accurate material model
development.
References cited in this section
46. P.S. Follansbee, High Strain Rate Deformation of FCC Metals and Alloys, Metallurgical Applications
of Shock Wave and High Strain Rate Phenomena, L.E. Murr, K.P. Staudhammer, and M.A. Meyers,
Ed., Marcel Dekker, 1986, p 451–480
94. S.R. Chen and G.T. Gray III, Constitutive Behavior of Tantalum and Tantalum-Tungsten Alloys,
Metall. Mater. Trans. A, Vol 27, 1996, p 2994–3006

95. E. El-Magd, H. Scholles, and H.P. Weisshaupt, The Stress-Strain Behaviour of Pure Metals and
Composite Materials in the Region of the Lüders Deformation under Dynamic Load Conditions,
DYMAT J., Vol 2, 1995, p 151–166
96. J. Harding, High-Rate Straining and Mechanical Properties of Materials, Explosive Welding, Forming
and Compaction, T.Z. Blazynski, Ed., Applied Science Publishers, London, 1983, p 123–158
97. T. Nicholas and A.M. Rajendran, Material Characterization at High Strain Rates, High Velocity Impact
Dynamics, J.A. Zukas, Ed., John Wiley & Sons Inc., 1990, p 127–296
98. J. Macdougall and J. Harding, Materials Testing for Constitutive Equations, J. Phys. (France) IV
Colloq., C3 (EURODYMAT 97), Vol 7, 1997, p 103–108
99. U.F. Kocks, Constitutive Equations for Slip, Constitutive Equations in Plasticity, A.S. Argon, Ed., MIT
Press, 1975, p 81–116
100. G.T. Gray III, Influence of Strain Rate on the Structure Property Behavior of Ti-48Al-1V,
Microstructure/Property Relationships in Titanium Aluminides and Alloys, Y.W. Kim and R.R. Boyer,
Ed., The Minerals, Metals and Materials Society, 1991, p 263–274
101. H. Quinney and G.I. Taylor, The Emission of the Latent Energy due to Previous Cold Working
when a Metal is Heated, Proc. R. Soc. (London) A, Vol 163, 1937, p 157–181
102. G.I. Taylor and W.S. Farren, The Heat Developed during Plastic Extension of Metals, Proc. R.
Soc. (London) A, Vol 107, 1925, p 422–451
103. D.R. Stull and G.C. Stinke, Thermodynamic Properties of the Elements, American Chemical
Society, 1956
Classic Split-Hopkinson Pressure Bar Testing
George T. (Rusty) Gray III, Los Alamos National Laboratory
Limitations and Problem Areas
In addition to the care needed to ensure the achievement of stress equilibrium during SHPB testing, several
other problems can be encountered during experimental investigations studying the mechanical behavior of
materials at high rates of loading. These problems are associated with inertia effects in the test machine, sample
constraint due to friction at the points of contact, and issues related to assuring accurate strain gage
measurements on the pressure bars.
Inertia. Even when the specimen has been evaluated to be deforming uniformly, longitudinal and radial inertia
caused by the rapid particle accelerations imposed during high strain-rate testing can influence the measured
stress-strain behavior (Ref 3, 104). The errors due to both longitudinal and radial inertia have been analyzed,
and corrections have been derived for these errors (Ref 42). This analysis states that:
(Eq 24)
where σ
m
is the measured stress, ρ
s
is the density of the specimen, ν is the Poisson's ratio, l
s
is the specimen
length, and d is the specimen diameter. This expression predicts that errors are minimized if the strain rate is
held constant or if the term inside the brackets is set to zero by choosing specimen dimensions such that

(Eq 25)
For a Poisson's ratio of 0.33, Eq 25 suggests that the optimum sample l
s
/d ratio to minimize errors caused by
inertia is 0.5. Further work by Bertholf and Karnes (Ref 105) using a full two-dimensional finite-difference,
elastoplastic finite-element analysis confirmed these results. This l
s
/d ratio is less than that determined to be the
most favorable for the minimization of errors due to friction in ASTM E 9, which specifies that 1.5 < l
s
/d < 2.0
(Ref 3). However, because the total strain in a split-Hopkinson pressure bar test is typically limited to
approximately 25% to reduce the area mismatch between the specimen and the pressure bar, samples with an
l
s
/d of 0.5 are not expected to introduce any serious errors.
Radial inertia considerations limit the strain rate for which the SHPB technique is valid to about 10
5
s
-1
for a
high sound-speed material. The reason for this limitation is that as the strain rate is increased, the specimen size
must be decreased accordingly. The specimen required eventually becomes so small that it no longer represents
bulk material response. Only very fine-grained materials, such as nanocrystalline-structured materials, with
high sound speeds can be tested with valid results at the very highest strain rates using this technique.
Friction is an important consideration in determining the validity of all compression testing (Ref 106). Further,
the assumption of uniaxial stress conditions in the specimen can be affected by the presence of frictional forces
that can cause radial traction at the interfaces between the pressure bars and the specimen. Lubrication is
therefore required at the specimen/pressure bar interfaces. The optimum l
s
/d ratio to minimize friction for a
split-Hopkinson pressure bar compression test specimen is approximately one-half that determined to be most
favorable for minimizing errors caused by friction for low-rate tests.
Early workers studying the SHPB were concerned about longitudinal inertial effects (i.e., how long it takes the
forces on the ends of the specimen to become equal, that is, the ringing up time). Accordingly, they tested thin
wafers of material with a thickness-to-diameter ratio of 0.1. Such extreme sample aspect ratios are known to
maximize the effect of friction as the measured yield pressure, p, is related to the material flow stress, σ
f
,
according to the relation (Ref 107):
(Eq 26)
where m is the ratio of the friction stress to the shear strength of the material, D is the specimen diameter, and l
s
is the specimen thickness (or length). Bell (Ref 108) identified that the absence of proper lubrication at the
pressure bar/sample interfaces can cause large discrepancies between the measured strain on the radial surface
of the specimen and the average strain obtained from the relative displacement of its two faces in the
compression split-Hopkinson bar test.
Care must be exercised, therefore, in lubricating samples prior to testing as well as to limiting the strain in a
single test to strains less than ~20 to 25%. Repeated reloading of a sample, with intermediate remachining to
ensure flat and parallel sample loading surfaces, can be utilized to achieve higher total strains. Repetitive
reloading offers the added benefit of minimizing adiabatic heating effects on the measured stress-strain
behavior. The size of the sample can also have a significant effect on the friction condition during an SHPB
test. Gorham (Ref 104) showed that larger samples of copper deformed at the same strain rate involve longer
radial displacement at higher velocities than in the case of smaller samples. Breakdown in the lubricant is more
likely under large displacements, and loss of lubricant by jetting is enhanced at increased strain rates. Care must
therefore be exercised to avoid velocity-dependent frictional constraints altering the stress-strain response if
larger test samples are used.
The use of an oil-based molybdenum disulfide lubricant has been shown to be effective for room-temperature
SHPB testing (Ref 3). For elevated-temperature tests, a thin layer of fine boron nitride powder can be used to
lubricate the specimen/pressure bar interfaces. So far, no lubricant has been found that completely eliminates
friction for metallic specimens in this geometry, although the frictional stresses can be reduced to about 4% of
the metal's shear strength. Friction can, in principle, be measured using annular specimens, the idea being that
the higher the friction, the smaller the ratio of the internal to external diameter for a given strain (Ref 107, 109).
However, the presence of a layer of lubricant at these interfaces can influence the timing between the waves
recorded on the incident and output pressure bars. Consequently, it is important to maintain as thin as possible
the layer of lubricant on the bar ends. Routine examination of the surface finish and flatness of the pressure-bar-
loading faces, in addition to checking for any possible cracking or erosion of the bar ends, are also critical
elements influencing valid SHPB data acquisition.
Strain-Gage Measurements. Because the stress-strain behavior of the material of interest is deduced from the
elastic strain signals in the pressure bars, the details of the conditions controlling the accuracy and
reproducibility of the strain gages are crucial. A number of considerations related to strain-gage installation and
usage can affect the elastic strain measurements obtained. Two gages generally are mounted at diametrically
opposite positions on each bar and connected so as to average out most bending strains in the bars and increase
the magnitude of the strain signal measured by a factor of two. The use of four gages arranged equidistantly
around the bar diameter, comprising a complete Wheatstone strain gage bridge, will totally eliminate any
bending effects on the strain data. The four-gage arrangement additionally corrects for any magnetostriction
effects (induced voltage in the strain gages due to stress wave propagation in a ferromagnetic bar material). Use
of nonmagnetic pressure bar materials, such as Ti-6Al-4V or Mg, eliminates any potential magnetostriction
errors in the strain-gage outputs. In addition to the elimination of bending forces through the use of multiple
gage locations, shielding of the wire leads from the strain gages to the signal conditioners is important for
minimizing external noise given the small magnitude of the absolute strain signals and the level of
amplification required to boost the signals to the levels required by the data acquisition system.
Finally, bonded strain gages have a finite-time-response capability that is linked to the stiffness of the epoxy
used to bond the gages to the bars as well as the thickness of the interface. Using an epoxy that is too compliant
can dampen the signals transferred from the bar surface to the strain gages. Conversely, an epoxy that is too
stiff and brittle will require frequent replacement. Careful selection, application, and maintenance of the gages
bonded to the SHPB is required to ensure accurate bar operation. Periodic calibration is used to monitor the
gage/epoxy bond degradation.
References cited in this section
3. P.S. Follansbee, The Hopkinson Bar, Mechanical Testing, Vol 8, ASM Handbook, American Society for
Metals, 1985, p 198–203
42. E.D.H. Davies and S.C. Hunter, The Dynamic Compression Testing of Solids by the Method of the Split
Hopkinson Pressure Bar (SHPB), J. Mech. Phys. Solids, Vol 11, 1963, p 155–179
104. D.A. Gorham, The Effect of Specimen Dimensions on High Strain Rate Compression
Measurements of Copper, J. Phys. D, Appl. Phys., Vol 24, 1991, p 1489–1492
105. I.D. Bertholf and C.H. Karnes, 2D Analysis of the Split Hopkinson Pressure Bar System, J.
Mech. Phys. Solids, Vol 23, 1975, p 1–19
106. J. Klepaczko and Z. Malinowski, Dynamic Frictional Effects as Measured from the Split
Hopkinson Pressure Bar, High Velocity Deformation of Solids, K. Kawata and J. Shioiri, Ed., Springer-
Verlag (Berlin), 1978, p 403–416
107. D.A. Gorham, P.H. Pope, and O. Cox, Sources of Error in Very High Strain Rate Compression
Tests, Inst. Phys. Conf. Series, Vol 70, 1984, p 151–158
108. J.F. Bell, An Experimental Diffraction Grating Study of the Quasi-Static Hypothesis of the
SHPB Experiment, J. Mech. Phys. Solids, Vol 14, 1966, p 309–327
109. S.M. Walley, P.D. Church, M. Furth, and J.E. Field, A High-Speed Photographic Study of the
Rapid Deformation of Metal Annuli: A Comparison of Theory with Experiment, J. Phys. (France) IV
Colloq., C3 (EURODYMAT 97), Vol 7, 1997, p 317–322

Classic Split-Hopkinson Pressure Bar Testing
George T. (Rusty) Gray III, Los Alamos National Laboratory
New Developments in Split-Hopkinson Bar Testing
The Hopkinson pressure bar, as a research and engineering tool for the quantitative measurement of the high-
rate stress-strain behavior of materials, is a technique that is far from static. In recent years, a number of new
improvements have been designed and their value proven to improve both the accuracy and timeliness of
measurements. One-, two-, and three-dimensional finite-element models of the split-Hopkinson pressure bar
have proven their ability to simulate test parameters and allow pretest setup validation checks as an aid to
planning. Finite-element models additionally offer a means in the future to validate the data and dispersion
analysis used in the Hopkinson bar to probe for the effects of inertia and friction, for example, and provide an
opportunity to extend the use of the Hopkinson bar to the characterization of materials for which the SHPB
technique was previously unable to achieve a valid uniaxial stress state. Previous research using this approach
on the SHPB testing and analysis of soil samples has shown the utility of such a finite element method
(FEM)/standard SHPB analysis (Ref 51). A current example of this promising line of research is applied to
split-Hopkinson bar testing of viscoplastic materials (more information can be found in the article “Split-
Hopkinson Pressure Bar Testing of Soft Materials” in this Volume).
Novel methods of characterizing sample diametrical strains are also being developed for the Hopkinson bar
using optical diagnostic techniques (Ref 110, 111). This technique offers an alternate mechanism to measure
the diametrical strain in a Hopkinson pressure bar sample as a function of time using a linear laser line-
measuring diagnostic device. This technique offers a valuable additional way to accurately measure sample
dimensional changes without the use of strain gages attached to the sample. This technique, however, must also
be cautiously approached as a stand-alone technique where anisotropic plasticity in the sample could falsely
portray the sample diametral strain unless multiple viewing points are surveyed. Additional optical techniques
are emerging that may provide a quantitative means of measuring axial and radial strains in SHPB samples
during testing. These techniques include monitoring strains on a cylindrical sample using Bragg grating sensors
(Ref 112) and the measurement of tangential displacements on samples and/or the pressure bars themselves
using speckle interferometry (Ref 113).
Finally, careful attention to controlling wave reflections in the SHPB has also opened new opportunities to
study defect/damage evolution in brittle materials during high-rate loading histories (Ref 114). Careful
momentum trapping of the transmitted and reflected wave pulses in the pressure bars can be utilized to facilitate
single pulse loading of the sample. Researchers are also exploring exciting new methods for in situ dispersion
measurements (Ref 47) on pressure bars, which offer opportunities for increased signal resolution in the future.
References cited in this section
47. X.J. Wu and D.A. Gorham, Stress Equilibrium in the Split Hopkinson Pressure Bar Test, J. Phys.
(France) IV Colloq., C3 (EURODYMAT 97), Vol 7, 1997, p 91–96
51. C.W. Felice, E.S. Gaffney, and J.A. Brown, Extended Split-Hopkinson Bar Analysis for Attenuating
Materials, J. Eng. Mech., Vol 117, 1991, p 1119–1135
110. V. Vallé, M. Cottron, and A. Lagarde, Dynamic Optical Method for Local Strain Measurements:
Principle and Characteristics, J. Phys. (France) IV Colloq., C8 (DYMAT 94), Vol 4, 1994, p 59–64
111. K.T. Ramesh and S. Narasimhan, Finite Deformations and the Dynamic Measurement of Radial
Strain on Compression Kolsky Bar Experiments, Int. J. Solids Struct., Vol 33, 1996, p 3723–3738
112. S.W. James, R.P. Tatam, S.R. Fuller, and C. Crompton, Monitoring Transient Strains on a Gun
Barrel Using Fibre Bragg-Grating Sensors, Meas. Sci. Technol., Vol 10, 1999, p 63–67
