ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

25. J.D. Campbell and W.G. Ferguson, The Temperature and Strain Rate Dependence of the Shear Strength

of Mild Steel, Philos. Mag., Vol 21, 1970, p 63–82

26. J. Harding and J. Huddart, The Use of the Double-Notch Shear Test in Determining the Mechanical

Properties of Uranium at Very High Rates of Strain, Inst. Phys. Conf. Ser., Vol 47, 1980, p 49–61

27. D. Ruiz, J. Harding, and C. Ruiz, The Double Notch Shear Test—Analysis and Development for

Material Testing at Very High Strain Rates, Structures under Shock and Impact, P.S. Bulson, Ed.,

Elsevier, Amsterdam, p 145–154

28. J.R. Klepaczko, An Experimental Technique for Shear Testing at High and Very High Strain Rates: The

Case of a Mild Steel, Int. J. Impact Eng., Vol 15, 1994, p 25–40

29. J.R. Klepaczko, H.V. Nguyen, and W.K. Nowacki, Quasi-Static and Dynamic Shearing of Sheet Metals,

Eur. J. Mech. A-Solids, Vol 18, 1999, p 271–289

30. J. Klepaczko, Application of the Split Hopkinson Pressure Bar to Fracture Dynamics, Inst. Phys. Conf.

Ser., Vol 47, 1980, p 201–214

31. G.I. Taylor, The Use of Flat Ended Projectiles for Determining Yield Stress, Part I: Theoretical

Considerations, Proc. R. Soc. (London) A, Vol 194, 1948, p 289–299

Classic Split-Hopkinson Pressure Bar Testing

George T. (Rusty) Gray III, Los Alamos National Laboratory

Principles of the Split-Hopkinson Pressure Bar

While there is no universal standard design for SHPB test apparatus, all facilities share common design

elements. A compression Hopkinson bar test apparatus consists of the following:

• Two long, symmetrical bars

• Bearing and alignment fixtures to allow the bars and striking projectile to move freely while retaining

precise axial alignment

• Compressed gas launcher/gun tube or alternate propulsion device for accelerating a projectile, termed

the striker bar, to produce a controlled compressive pulse in the incident bar

• Strain gages mounted on both bars to measure the stress-wave propagation in the bars

• Associated instrumentation and data acquisition system to control, record, and analyze the stress-wave

data in the bars (Ref 18)

In a compression split-Hopkinson pressure bar, a sample is sandwiched between an elastic incident and a

transmitted bar (Fig. 1). The terms incident/input and transmitted/output are used interchangeably throughout

this article to describe the two pressure bars used in the SHPB. The elastic displacements measured in these

bars are in turn used to determine the stress-strain conditions at each end of the sample.

Fig. 1 Schematic of a compression split-Hopkinson pressure bar

The bars used in a split-Hopkinson bar setup are traditionally constructed from a high-strength structural metal,

AISI-SAE 4340 steel, maraging steel, or a nickel alloy such as Inconel. Such construction is used because the

yield strength of the selected pressure bar material determines the maximum stress attainable within the

deforming specimen given that the pressure bars must remain elastic. Inconel bars have been previously used

for elevated-temperature Hopkinson bar testing because this alloy's elastic properties are essentially invariant

up to 800 °C (Ref 3). Because a lower-modulus material increases the signal-to-noise level, the selection of a

bar material with lower strength and lower elastic modulus material for the bars is sometimes desirable to

facilitate high-resolution dynamic testing of low-strength materials such as polymers or foams. Researchers

have selected bar materials possessing a range of elastic stiffnesses from maraging steel (210 GPa) to titanium

(110 GPa) to aluminum (90 GPa) to magnesium (45 GPa) (Ref 5, 32), and finally, to polymer bars (<20 GPa)

(Ref 17, 33, 34, 35). Alternately, the signal-to-noise of a Hopkinson bar used to test polymeric materials can be

increased using a hollow tubular transmitted pressure bar (Ref 36). While this technique can yield increased

transmitted wave measurement sensitivity, the absolute resolution of the sample stress-strain data for polymeric

materials must still address the elastic wave dispersion in the tubular-transmitted bar (Ref 37, 38).

The length, l, and diameter, d, of the pressure bars are chosen to meet a number of criteria for test validity as

well as the maximum strain rate and strain level desired in the sample. The length of the pressure bars must first

ensure one-dimensional wave propagation for a given pulse length; for experimental measurements on most

engineering materials, this propagation requires approximately 10 bar diameters. To readily allow separation of

the incident and reflected waves for data reduction, each bar should exceed a length-to-diameter (L/D) ratio of

~20. In addition, the maximum strain rate desired will influence the selection of the bar diameter because the

highest strain-rate tests require the smallest diameter pressure bars (this aspect of bar design is discussed in a

later section). The third consideration affecting the selection of the bar length is the amount of total strain

desired to be imparted into the specimen; the absolute magnitude of this strain is related to the length of the

incident wave. The pressure bar must be at least twice as long as the incident wave if the incident and reflected

waves are to be recorded without interference. In addition, because the bars must remain elastic during the test,

the displacement and velocity of the bar interface between the sample and the bar can be accurately determined.

Depending on the sample size, for strains >30% it may be necessary for the split-Hopkinson bars to have an

L/D ratio of 100 or more (Ref 3). There are similar requirements for bar L/D ratios to allow wave separation for

compression, tensile, and torsion Hopkinson bars.

For proper Hopkinson bar operation, the bars must be physically straight, free to move without binding, and

carefully mounted to ensure optimal axial alignment. Precision bar alignment is required for both uniform and

one-dimensional wave propagation within the pressure bars as well as for uniaxial compression within the

specimen during loading. Bar alignment cannot be forced by overconstraining or forceful clamping of curved

pressure bars in an attempt to straighten them because this clamping violates the boundary conditions for one-

dimensional wave propagation in an infinite cylindrical solid. Lack of free movement of the bars will lead to

additional noise on the wave forms measured on the pressure bars. Bar motion must not be impeded by the

mounting bushings but rather must remain free to readily move along the bar axis. Accordingly, it is essential to

apply precise dimensional specifications during construction and assembly. Pressure bars are often centerless

ground along their length to achieve the uniform diameter and straightness required. In typical bar installations,

as schematically shown in Fig. 1, the pressure bars are mounted to a common rigid base to provide a rigid and

straight mounting platform. Construction of the Hopkinson pressure bar facility, compression, tension, or

torsion, on an optical rail beam rigidly attached to an I-beam, can be used to facilitate reproducible alignment.

Figure 2 shows one of the compression Hopkinson bar facilities at Los Alamos National Laboratory, where an

optical rail is used to maintain accurate pressure bar alignment. Individual mounting brackets or stanchions with

slip bearings through which the bars pass are typically spaced every 200 to 300 mm (8 to 12 in.), depending on

the bar diameter and stiffness. Mounting brackets are generally designed s o that they can be individually

translated to adjust bar alignment within each stanchion.

Fig. 2 A compression split-Hopkinson pressure bar facility at Los Alamos National Laboratory

The most common method of generating an incident wave in the input bar is to propel a striker bar to impact

the end of the incident bar. The striker bar is normally fabricated from the same material and is of the same

diameter as the pressure bars. The length and velocity of the striker bar are chosen to produce the desired total

strain and strain rate within the test specimen. While elastic waves can also be generated in an incident bar

through the adjacent detonation of explosives at the free end of the incident bar, as Hopkinson did (Ref 7), it is

more difficult to ensure a one-dimensional excitation within the incident bar by direct explosive loading.

The impact of a striker bar on the free end of the incident bar develops a longitudinal compressive incident

wave in this bar, designated ε

, as denoted in Fig. 3. Once this wave reaches the bar-specimen interface, a part

of the pulse, designated ε

, is reflected while the remainder of the stress pulse passes through the specimen and,

upon entering the output bar, is termed the transmitted wave, ε

. The time of passage and magnitude of these

three elastic pulses through the incident and transmitted bars are recorded by strain gages normally cemented at

the midpoint positions along the length of the two pressure bars. Figure 3 shows an illustration of the strain-

gage data measured as a function of time for the three wave signals during the testing of a 304L stainless steel

sample using maraging steel pressure bars. The incident and transmitted wave signals represent compressive

loading pulses, while the reflected wave is a tensile wave.

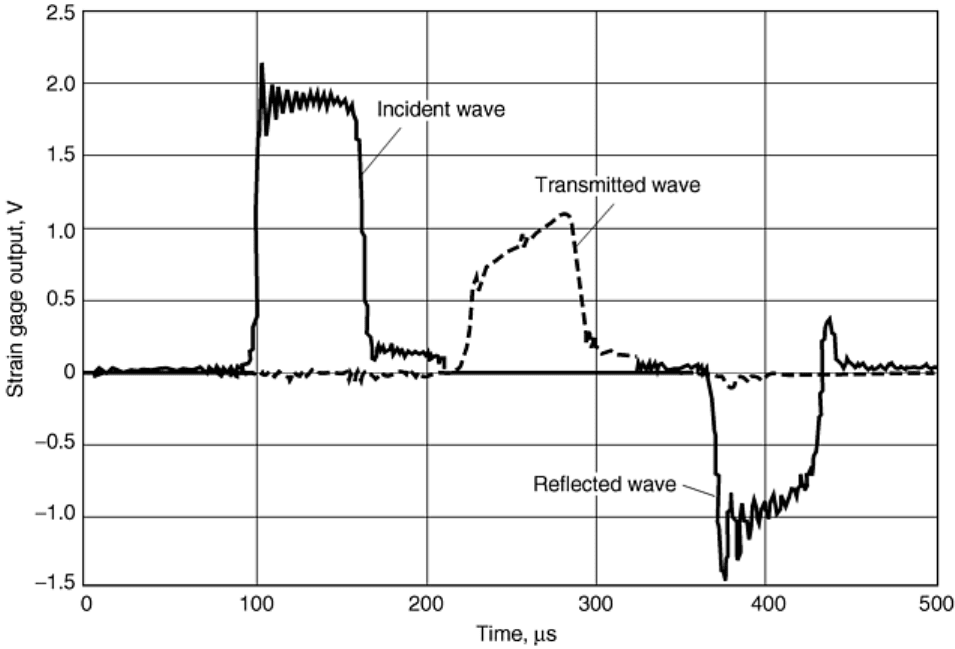
Fig. 3 Strain-gage data, after signal conditioning and amplification, from a compression split-Hopkinson

pressure bar test of a 304 stainless steel sample showing the three stress waves measured as a function of

time. Note that the wave positions in time are arbitrarily superimposed due to the time delays used

during data acquisitions.

Using the wave signals from the gages on the incident and transmitted bars as a function of time, the forces and

velocities at the two interfaces between the pressure bars and the specimen can be determined. When the

specimen is deforming uniformly, the strain rate within the specimen is directly proportional to the amplitude of

the reflected wave. Similarly, the stress within the sample is directly proportional to the amplitude of the

transmitted wave. (termed the 1-wave stress as discussed later). The reflected wave is also integrated to obtain

strain and is plotted against stress to give the dynamic stress-strain curve for the specimen.

References cited in this section

3. P.S. Follansbee, The Hopkinson Bar, Mechanical Testing, Vol 8, ASM Handbook, American Society for

Metals, 1985, p 198–203

5. J.E. Field, S.M. Walley, N.K. Bourne, and J.M. Huntley, Review of Experimental Techniques for High

Rate Deformation Studies, Proc. Acoustics and Vibration Asia '98 (Singapore), 1998, p 9–38

7. B. Hopkinson, A Method of Measuring the Pressure Produced in the Detonation of High Explosives or

by the Impact of Bullets, Philos. Trans. R. Soc. (London) A, Vol 213, 1914, p 437–456

17. H. Zhao and G. Gary, On the Use of SHPB Techniques to Determine the Dynamic Behavior of

Materials in the Range of Small Strains, Int. J. Solids Struct., Vol 33, 1996, p 3363–3375

18. G.T. Gray III, High-Strain-Rate Testing of Materials: The Split-Hopkinson Pressure Bar, Methods in

Materials Research, E. Kaufmann, Ed., John Wiley Press, 1999, in press

32. G.T. Gray III, D.J. Idar, W.R. Blumenthal, C.M. Cady, and P.D. Peterson, High- and Low-Strain Rate

Compression Properties of Several Energetic Material Composites as a Function of Strain Rate and

Temperature, 11th Detonation Symposium, 1998 (Snow Mass, CO), J. Short, Ed., in press

33. G. Gary, J.R. Klepaczko, and H. Zhao, Generalization of Split Hopkinson Bar Technique to Use

Viscoelastic Materials, Int. J. Impact Eng., Vol 16, 1995, p 529–530

34. G. Gary, L. Rota, and H. Zhao, Testing Viscous Soft Materials at Medium and High Strain Rates,

Constitutive Relation in High/Very High Strain Rates, K. Kawata and J. Shioiri, Ed., Springer-Verlag,

Tokyo, 1996, p 25–32

35. G.T. Gray III, W.R. Blumenthal, C.P. Trujillo, and R.W. Carpenter II, Influence of Temperature and

Strain Rate on the Mechanical Behavior of Adiprene-L100, J. Phys. (France), C3 (DYMAT 97), Vol 7,

1997, p 523–528

36. W. Chen, B. Zhang, and M.J. Forrestal, A Split Hopkinson Bar Technique for Low-Impedance

Materials, Exp. Mech., Vol 39, 1999, p 1–5

37. I. Mirsky and G. Herrmann, Axially Symmetric Motions of Thick Cylindrical Shells, J. Appl. Mech.

(Trans. ASME), Vol 25, 1958, p 97–102

38. G. Herrmann and I. Mirsky, Three-Dimensional and Shell-Theory Analysis of Axially Symmetric

Motions of Cylinders, J. Appl. Mech. (Trans. ASME), Vol 23, 1956, p 563–568

Classic Split-Hopkinson Pressure Bar Testing

George T. (Rusty) Gray III, Los Alamos National Laboratory

Theory of the Split-Hopkinson Pressure Bar

The determination of the stress-strain behavior of a material being tested in a Hopkinson bar, whether it is

loaded in compression as in the present illustration or in a tensile or torsion bar configuration, is based on the

same principles of one-dimensional elastic-wave propagation within the pressure loading bars as previously

reviewed (Ref 1, 3, 16, 18, 39).

As identified originally by Hopkinson (Ref 7) and later refined by Kolsky (Ref 13), the use of a long elastic bar

to study high-strain-rate mechanical behavior of materials is feasible using remote elastic bar measures of

sample response because the wave propagation behavior in such a geometry is well understood and

mathematically predictable. Accordingly, the displacements or stresses generated at any point can be deduced

by measuring the elastic wave at any point, x, as it propagates along the bar (Ref 3, 18, 40).

The subscripts 1 and 2 are used in this description to denote the incident and transmitted bar ends of the

specimen, respectively. The strains in the bars are then designated as ε

, ε

, and ε

(incident, reflected, and

transmitted strains, respectively) and the displacements of the ends of the specimen as u

and u

at the incident

bar-specimen and specimen-transmitted bar interfaces as given schematically in the enlarged view of the test

specimen in Fig. 4.

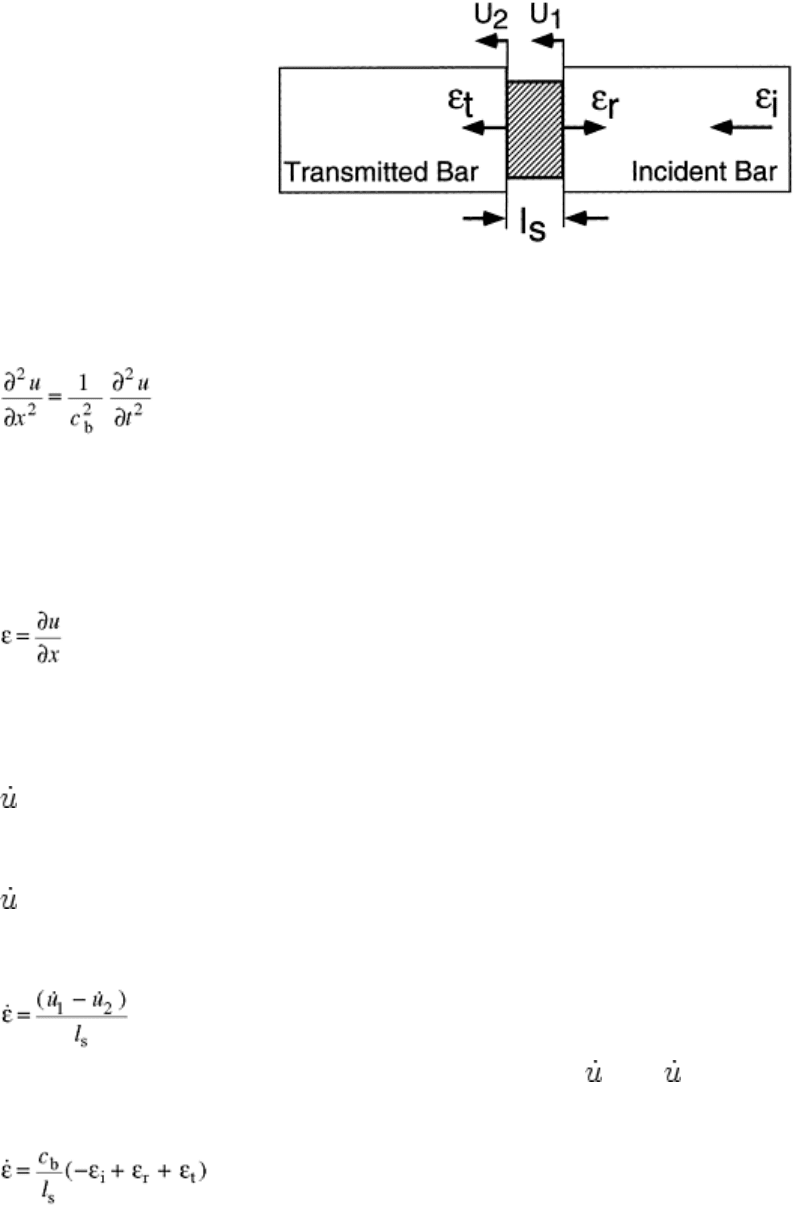
Fig. 4 Expanded view of incident (input) bar/specimen/transmitted (output) bar region

From elementary wave theory, it is known that the solution to the wave equation:

(Eq 1)

can be written as:

u = f(x - c

t) + g(x + c

t) = u

+ u

(Eq 2)

for the incident (input) bar, where f and g are functions describing the incident and reflected wave shapes, and

is the longitudinal wave speed in the pressure bars.

By definition, the 1-D strain is given by:

(Eq 3)

Therefore, differentiating Eq 2 with respect to x, the strain in the incident rod is given by:

ε = f′ + g′ = ε

+ ε

(Eq 4)

Differentiating Eq 2 with respect to time and using Eq 4 gives:

= c

(-f′ + g′) = c

(-ε

+ ε

)

(Eq 5)

for the incident bar.

The time derivative of the displacement in the transmitted bar, u = h(x - c

t), yields:

= −c

(Eq 6)

in the transmitted bar. Equations 5 and 6 are true everywhere, including at the ends of the pressure bars. The

strain rate in the test specimen is:

(Eq 7)

where l

is the instantaneous length of the specimen, and

and

are the velocities at the incident bar-

specimen and specimen-transmitted bar interfaces, respectively.

Substituting Eq 5 and 6 into Eq 7 gives:

(Eq 8)

By definition, the forces in the two bars are:

= AE(ε

+ ε

)

(Eq 9)

and

= AEε

(Eq 10)

where A is the cross-sectional area of the pressure bar, and E is the Young's elastic modulus of the bars

(normally equal, given that identical material is used for both the incident and transmitted pressure bars).

After an initial “ringing-up” period, where the exact duration or period depends on the sample sound speed and

sample geometry (in particular, its length), it is assumed that the specimen is in force equilibrium, and the

specimen is deforming uniformly. If these assumptions are valid, a simplification can be made equating the

forces on each side of the specimen (i.e., F

= F

). Comparing Eq 9 and 10, therefore, means that

= ε

+ ε

(Eq 11)

Substituting this criterion into Eq 8 yields:

(Eq 12)

The engineering stress, or conventional stress, in conventional mechanical testing of materials is calculated

from the force divided by the sample original area, A

. Because of the constancy of volume in incompressible

solids, A

= A

, (where l

is the original length of the specimen, A

is the original cross-sectional area, and A

is the instantaneous cross-sectional area of the sample) (Ref 41). Expressions for the strain can therefore be

written in terms of either the length or the area of the test sample. Accordingly, the true stress is calculated from

the strain-gage-signal measure of the transmitted force divided by the instantaneous cross-sectional area, A

, of

the specimen over which it acts:

(Eq 13)

The importance of this requirement to all types of Hopkinson bar testing using the one-dimensional wave

assumptions detailed is that true stress in a sample in the Hopkinson bar cannot be extracted for materials

whose volumes are not conserved. The instantaneous sample area used in Eq 13 is deduced from the reflected

strain signal in the incident bar assuming that the constancy of volume assumption is valid in the sample (i.e.,

there is a fixed relationship between sample cross-sectional area and its length). Without this assumption, there

is no basis for using the transmitted signal to measure force and the reflected wave to extract strain in the

sample. Materials for which this problem exists include metallic and polymeric foams, honeycomb structures,

and porous compacts for which mechanical loading produces compaction, densification, or porosity during

testing. Valid Hopkinson bar testing of materials for which the constant volume criterion is not valid, therefore,

requires additional sample diagnostics during the duration of the test to calculate true stress. Simultaneous use

of high-resolution high-speed photography can be used to monitor sample length and diameter during testing.

The photographic data, once digitized, can then be used to measure the actual strain rate and true strain as a

function of time in the sample. Such data, when combined with the transmitted wave-data measuring force, can

provide the needed data to calculate true stress.

Given that the volume constancy requirement is satisfied in the sample, Eq 12 and 13 can be used to determine

the dynamic stress-strain curve of the sample. This analysis is termed a 1-wave analysis because it uses only the

reflected wave to calculate strain in the sample, and only the transmitted wave is used to calculate the stress in

the sample. The 1-wave analysis assumes that stress equilibrium is ensured in the sample (i.e., as a function of

time, the stress and strain in the sample are uniform along its length). Conversely, the stress in the sample at the

incident bar-sample interface can be calculated using a momentum balance of the incident and reflected wave

pulses, termed a 2-wave stress analysis because it is a summation of the two waves at this interface. However, it

is known that such a condition cannot be correct at the early stages of any test because of the transient effect

that occurs when loading starts at the incident bar-specimen interface while the other sample face remains at

rest. Given finite stress-wave propagation through the sample, time is required for stress-state equilibrium to be

achieved. Reduced sound speed and high radial inertia in the sample will increase this problem (Ref 32).

Previous researchers have additionally adopted a 3-wave stress analysis, which averages the forces on both ends

of the specimen to track the ringup of the specimen to a state of stable stress (Ref 18, 40). The term 3-wave

indicates the use of all three waves to calculate an average stress in the sample, the transmitted wave to

calculate the stress at the specimen-transmitted interface (back stress), and the combined incident and reflected

pulses to calculate the stress at the incident bar-specimen interface (front stress). In the 3-wave case, the

specimen stress is then simply the average of the two forces divided by the combined interface areas:

(Eq 14)

Substituting Eq 9 and 10 into Eq 14 then gives:

(Eq 15)

From these equations, the average stress-strain curve of the specimen can be computed from the measured

reflected and transmitted strain pulses as long as the volume of the specimen remains constant and the sample is

free of barreling (i.e., friction effects are minimized).

References cited in this section

1. U.S. Lindholm, High Strain Rate Testing, Part 1: Measurement of Mechanical Properties, Techniques of

Metals Research, Vol 5, R.F. Bunshah, Ed., Wiley Interscience, New York, 1971, p 199–271

3. P.S. Follansbee, The Hopkinson Bar, Mechanical Testing, Vol 8, ASM Handbook, American Society for

Metals, 1985, p 198–203

7. B. Hopkinson, A Method of Measuring the Pressure Produced in the Detonation of High Explosives or

by the Impact of Bullets, Philos. Trans. R. Soc. (London) A, Vol 213, 1914, p 437–456

13. H. Kolsky, An Investigation of the Mechanical Properties of Materials at Very High Rates of Loading,

Proc. Phys. Soc. (London), Vol 62B, 1949, p 676–700

16. V.P. Muzychenko, S.I. Kashchenko, and V.A. Guskov, Use of the Split Hopkinson Pressure Bar

Method for Examining the Dynamic Properties of Materials: Review, Ind. Lab. (USSR), Vol 52, 1986, p

72–83

18. G.T. Gray III, High-Strain-Rate Testing of Materials: The Split-Hopkinson Pressure Bar, Methods in

Materials Research, E. Kaufmann, Ed., John Wiley Press, 1999, in press

32. G.T. Gray III, D.J. Idar, W.R. Blumenthal, C.M. Cady, and P.D. Peterson, High- and Low-Strain Rate

Compression Properties of Several Energetic Material Composites as a Function of Strain Rate and

Temperature, 11th Detonation Symposium, 1998 (Snow Mass, CO), J. Short, Ed., in press

39. M.M. Al-Mousawi, S.R. Reid, and W.F. Deans, The Use of the Split Hopkinson Pressure Bar

Techniques in High Strain Rate Materials Testing, Proc. Inst. Mech. Eng., Part C: J. Mech. Eng. Sci.,

Vol 211, 1997, p 273–292

40. P.S. Follansbee and C. Frantz, Wave Propagation in the SHPB, J. Eng. Mater. Technol. (Trans. ASME),

Vol 105, 1983, p 61–66

41. G.E. Dieter, Mechanical Metallurgy, McGraw-Hill, Inc., 1976

Classic Split-Hopkinson Pressure Bar Testing

George T. (Rusty) Gray III, Los Alamos National Laboratory

Practical Aspects of the Split-Hopkinson Pressure Bar

Calibration. To analyze the strain-gage data from a split-Hopkinson pressure bar test, the system must be

calibrated prior to testing (Ref 3, 18). Calibration of the entire Hopkinson bar setup is obtained in situ by

comparing the constant amplitude of a wave pulse with the impact velocity of the striker bar for each bar

separately, termed “bars apart.” Operationally, this calibration is accomplished by inputting a known velocity

pulse into the input bar, and then, in turn, the transmitted bar, with no sample present. Thereafter, impact of the

striker with the input bar in direct contact with the transmitted bar, with no specimen, gives the coefficient of

transmission, termed “bars together.” Accurate measurement of the velocity, V, of the striker bar impact into a

pressure bar is linearly related by:

(Eq 16)

where ε

is the strain in the incident or transmitted bar, depending on which is being calibrated, and c

is the

longitudinal wave speed in the bar if the impacting striker bar and the pressure bar are the same material and

have the same cross-sectional area. Careful measurement of the striker velocity, using a laser interruption

scheme or shorting pins, for example, in comparison with the elastic strain signal in a pressure bar, can then be

used to calculate a calibration factor for the pressure bar being calibrated. Accurate measurement of the

longitudinal-wave velocity in the pressure bars being used is critical. The use of textbook values is not advised.

Variations in alloy chemistry, microstructure, and heat treatment from the manufacturer can all lead to

measurable variations in the longitudinal wave speed in the pressure bars and should not be assumed to be a

constant but rather measured for each set of bars used. Calibration values also include validation due to strain-

gage response, including cement or epoxy interfaces, wiring, amplifiers, and so on. Calibrations should be

verified periodically, especially when changes are made to either mechanical or electronic components.

Optimal data resolution also requires careful design of the sample size for a given material as well as the

selection of an appropriate striker bar length and velocity to achieve test goals. The determination of the

optimal sample length first requires consideration of the sample rise time, t, required for a uniform uniaxial

stress state to be achieved within the sample. It has been estimated (Ref 42) that this rise time is the time

required for three (actually π) reverberations of the stress pulse within the specimen (Ref 3). For a plastically

deforming solid that obeys the Taylor-von Karman theory, time follows the relationship:

(Eq 17)

Here, ρ

is the density of the specimen, l

is the specimen length, and ∂σ/∂ε is the stage 2 work-hardening rate of

the true stress/true strain curve for the material to be tested. For rise times less than that given by Eq 17, the

sample should not be assumed to be deforming uniformly, and stress-strain data will accordingly be in error.

Materials possessing either high work-hardening rates, slow sound speeds, and/or high densities will require

shorter sample lengths to facilitate rapid ringup and, therefore, rapid attainment of a uniaxial stress state in the

sample.

One approach for achieving a uniform stress state during split-Hopkinson pressure bar testing is to decrease the

sample length such that the rise time, t, from Eq 17 is as small as possible. Other considerations of scale, which

are described in the sample design section, limit the range of L/D ratios appropriate for a given material; the

specimen length may not be decreased without a concomitant decrease in the specimen and bar diameters. The

use of small diameter bars (<6 mm) to achieve higher strain rates is a common practice in split-Hopkinson

pressure bar testing (Ref 3).

Pulse Shaping. Because the value of t from Eq 17 has a practical minimum, an alternate method to facilitate

stress-state equilibrium at low strains is to increase the rise time of the incident wave. Use of impedance-

matched materials for the striker and incident bar (i.e., a symmetric impact) yields a short rise-time pulse,

which approximates a square wave. The rise time of such a square-wave pulse is likely to be less than t in Eq 16

in most instances. Contrarily, if the rise time of the incident wave pulse is increased to a value more comparable

with the time to ring up the specimen, then the data will be valid at an earlier strain. Furthermore, because the

highly dispersive short wavelength components arise from the leading and trailing edges in the incident wave, a

longer rise-time pulse will contain fewer of these components than will a sharply rising pulse (Ref 3, 43). The

consequence of this solution is a lower applied strain rate.

Experimentally, the rise time of the incident wave can be increased by placing a soft, deformable metal shim

between the striker and the incident bar during impact. The choice of material and thickness for this shim, or tip

material (Ref 43), depends on the desired strain rate and the strength of the specimen. Typically, the tip material

is selected to have the same strength as the specimen and is 0.1 to 2 mm (0.004 to 0.08 in.) in thickness. An

additional benefit of this layer is that it can result in a more uniform strain rate throughout the experiment.

However, for thick shims the strain rate will not be constant and will ramp up during the test. The exact