ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control

Подождите немного. Документ загружается.

The generality of the capability characterization is limited to the application for which the experiment is representative.

Either important factors must be typical of the application or random samples must be chosen from the population of

interest and repeat inspections performed for these factors. For example, if a single inspector is used to characterize a

fluorescent penetrant inspection, it must be assumed that this inspector is typical of all the inspectors in the shop. An

alternative might be to choose a random sample of inspectors from the total pool and have each of the selected inspectors

perform the experiment.

Depending on the application of the results of the experiment, stratified sampling may be required to obtain a

representative sample. For instance, if the capability will apply to two facilities and one of them inspects twice as many

components as the other, then that facility should have twice as many inspectors in the experiment. An alternative method

is to characterize each facility independently. Care is then required in combining the results for the joint characterization.

Factorial Experiments for Hit/Miss Data. The analysis for the hit/miss data requires that all factors be balanced in

any one analysis. When practical, this can be most easily achieved by performing complete factorial experiments. For

example, Table 1 contains the results of a two-factor experiment, with the factors being cracks and inspectors. These data

can be analyzed as one data set with three inspections per crack. The resulting POD(a) function and its confidence bound

would be representative of the population of inspectors from which the sample was drawn.

If the effect of a third factor, for example, different lots of penetrants, were to be included, the entire experiment would be

repeated for each of the lots chosen at random from the population of all lots. If three lots were sampled, a total of nine

inspections would be performed on each of the flawed specimens, and the resulting POD(a) would apply to the entire

inspection process. Suppose, however, that the second and third samples of penetrant were used only by Inspector A. In

this case, the two additional sets of inspection data cannot be combined with the other three in a single analysis, because

the triple representation of Inspector A would bias the resulting POD(a) function toward his specific capability. The three

sets of inspection results for Inspector A can be combined, but the range of applicability of the answer is limited to

Inspector A (unless it can be shown or assumed that Inspector A is representative of the entire population).

When many factors must be considered, the number of possible combinations in a factorial experiment can easily become

prohibitive. More sophisticated experimental designs (fractional replications, for example) may then be required. In such

cases, the assistance of a professional statistician is recommended.

Experimental Design for Data. Inspection-result data in the form contain considerably more information than

hit/miss data and, as a consequence, permit more flexibility in the design of the experiment. In analysis, the parameters

of the POD(a) function are estimated from the slope, intercept, and standard deviation of residuals of the ln ( ) versus ln

(a) relation, as given by Eq 9, 12, and 13. In Eq 9, can be considered to be the sum of random effects, and experiments

can be designed to estimate the components of the total variation in . For example, operators, probes, and repeatability

can be jointly evaluated in a factorial experiment and their effects accounted for in the estimate of POD(a). The statistical

model for this experiment would be:

ln ( ) = β

+ β

ln (a) + C

+ O

+ P

+ R

+ (interaction terms)

(Eq 14)

where C

, O

, P

, and R

are the random effects due to cracks, operators, probes, and repeats, respectively. The random

term, δ of Eq 9, is the sum of all random effects. It can be assumed that the mean and variance of random effect X are zero

and , respectively. Then:

= + + + + . . .

(Eq 15)

Therefore, β

and β

can be estimated from a regression analysis, and can be estimated from the components of

variance using the expected mean squares for the random effects.

In principle, any statistical design from which the components of variance can be estimated can be used in an NDE

reliability experiment. However, the analysis methods would be specific to the particular design, and it is beyond the

scope of this article to address the general problem. In the section "Signal Response Analysis" in this article, it will be

assumed that only the variation due to cracks and one other factor is being investigated. It is recommended that the

assistance of a qualified statistician be obtained for more sophisticated experimental designs.

Sample Sizes and Flaw Sizes

Sample sizes in NDE reliability experiments are driven more by the economics of specimen fabrication and

characterization than by the desired degree of precision in the estimate of the POD(a) function. Although apparently

reasonable POD(a) functions can often be obtained from applying the maximum likelihood analysis to relatively few test

results, the confidence bound calculation is based on asymptotic (large sample) properties of the estimates. It should be

emphasized that the calculations can also produce totally unacceptable results from the relatively few test results or from

data that are not reasonably represented by the assumptions of the models. Therefore, there are minimal sample size

requirements that must be met to provide a degree of reasonable assurance in the characterization of the capability of the

system.

Larger sample sizes in NDE reliability experiments will, in general, provide greater precision in the estimate of the

POD(a) function. However, the sample size is determined from the number of cracks in the experiment, and there is a

coupling with the flaw sizes that must also be considered. The effect of this coupling manifests itself differently for the

hit/miss and analyses.

Sample Size Requirements for Hit/Miss Analysis. Data from hit/miss experiments are generally not amenable to

testing assumptions regarding the form of the POD(a) model. These tests require either large numbers of independent

inspections on each flaw of a specimen set or inspection results from an extremely large number of compatible specimens

(Ref 3, 4). Number and size considerations in hit/miss experiments are directed at their effect on the sampling properties

of the parameters of the POD(a) function (Ref 9).

In the hit/miss analysis, the output of an inspection states only whether or not a crack of known length was found in the

inspection (Table 1). There are probabilities associated with the outcomes, and the analysis assumes that this probability

increases with flaw size. Because it has been assumed that the inspection process is in a state of control, there is a range of

flaw sizes over which the POD(a) function is rising. In this flaw size range of uncertainty, the inspection system has

limited discriminating power in the sense that detecting or failing to detect would not be unusual. Such a range might be

defined by the interval (a

0.10

, a

0.90

), where a

denotes the flaw size that has probability of detection equal to p; that is:

POD(a

) = p

(Eq 16)

Flaws smaller than a

0.10

would then be expected to be missed, and flaws greater than a

0.90

would be expected to be

detected.

In a hit/miss reliability experiment, flaws outside the range of uncertainty do not provide as much information concerning

the POD(a) function as cracks within this range. Cracks in the almost-certain detection range and almost-certain miss

range provide very little information concerning probability of detection. Therefore, in the hit/miss experiment, not all

flaws convey the same amount of information, and the effective sample size is not necessarily the total number of flaws in

the experiment. Adding a large number of very large flaws does not increase the precision in the estimate of the

parameters of the POD(a) function.

In a reliability experiment, the location of the increasing range of the POD(a) function is not known. Further, the same

sets of specimens are often used in many different experiments. Therefore, it is not possible to fabricate a set of

specimens with optimal flaw sizes for a particular experiment. To minimize the chances of completely missing the crack

size range of maximum information and to accommodate the multiple uses of specimens, flaw sizes should be uniformly

distributed between the minimum and maximum of the sizes of potential interest. A minimum of 60 flaws should be

distributed in this range, but as many as economically possible should be used.

Sample Size Requirements for Analysis. The recorded signal response, , provides significantly more

information for analysis. In particular, the POD(a) model is derived from the correlation of the versus a data, and the

assumptions concerning the POD(a) model can be tested using the signal response data. Further, the pattern of

responses can indicate an acceptable range of extrapolation. Therefore, the range of crack sizes in the experiment is not as

critical in an analysis as in a hit/miss analysis. For example, if the decision threshold in Fig. 5 were set at 250 counts, all

but four of the cracks would have been detected. The larger cracks would have provided little information about the

POD(a) function in a hit/miss analysis. In an analysis, however, all of the recorded values provided full information

concerning the relation between signal response and crack size, and the values at the signal threshold and saturation limit

provided partial information. The linearity of the fit, the normality of the deviations, and the constancy of the residual

variation can all be easily evaluated from the versus a plot.

Because of the added information in the data, it is recommended that at least 30 flaws be present in experiments whose

results can be recorded in this form. Increasing the number of flaws increases the precision of the estimates, so the test set

should contain as many flawed specimens as economically feasible.

Unflawed Inspection Sites. In the context of the analyses presented in this section, sample size refers to the number

of known flaws in the specimens to be inspected. The total specimen set should also contain at least twice this number of

unflawed inspection sites. The unflawed sites are necessary to ensure that the NDE procedure is discriminating between

flawed and unflawed sites and to provide an estimate of the false call rate.

Although the false call rate can have important economic consequences, the NDE reliability analyses in this section were

dictated by the requirements of damage tolerance analyses. The primary objective was to estimate the chances of missing

flaws that might lead to structural failures. The concepts of these NDE reliability analyses can be generalized to include a

non-zero probability of a flaw indication when no flaw is present at an inspection site, that is, POD(a = 0) > 0.

References cited in this section

W.H. Lewis, W.H. Sproat, B.D. Dodd, and J.M. Hamilton, "Reliability of Nondestructive Inspections--

Final

Report," SA-ALC/MME 76-6-38-1, San Antonio Air Logistics Center, Kelly Air Force Base, Dec 1978

A.P. Berens and P.W. Hovey, "Evaluation of NDE Reliability Characterization," AFWAL-TR-81-

4160, Vol

1, Air Force Wright-Aeronautical Laboratories, Wright-Patterson Air Force Base, Dec 1981

A.P. Berens and P.W. Hovey, The Sample Size and Flaw Size Effects in NDI Reliability Experiments, in

Review of Progress in Quantitative Nondestructive Evaluation 4B,

D.O. Thompson and D.E. Chimenti, Ed.,

Plenum Press, 1985

NDE Reliability Data Analysis

Alan P. Berens, University of Dayton Research Institute

Maximum Likelihood Analysis

Parameter estimation based on the principle of maximizing the likelihood of an observed sample of data is a standard

statistical technique and is amply described in the literature (Ref 10, 11). The purpose of this section is to summarize the

method and its asymptotic sampling distribution properties in the context of analyzing NDE reliability data. Further, a

method for using this information to calculate lower confidence bounds on the POD(a) function is also presented.

Parameter Estimation. Let X

represent the outcome of the ith inspection and f(X

;θ) represent the probability of

obtaining X

, where θ= (θ

, θ

,. . .θ

)' is the vector of the k parameters in the probability model. For example, in a hit/miss

experiment, X

would be 0 or 1 with probability defined by Eq 4, where a is the size of flaw i and θ= (μ,σ)'. In an versus

a experiment, X

is the log of the signal response, and f(X

;θ) is a normal density function with mean and standard

deviation given by θ= (β

+ β

ln a, σ )', as defined in Eq 9. Let X

,. . ., X

represent the results of independent inspections

of n flaws. The likelihood, L, of a specific result is given by the likelihood function:

(Eq 17)

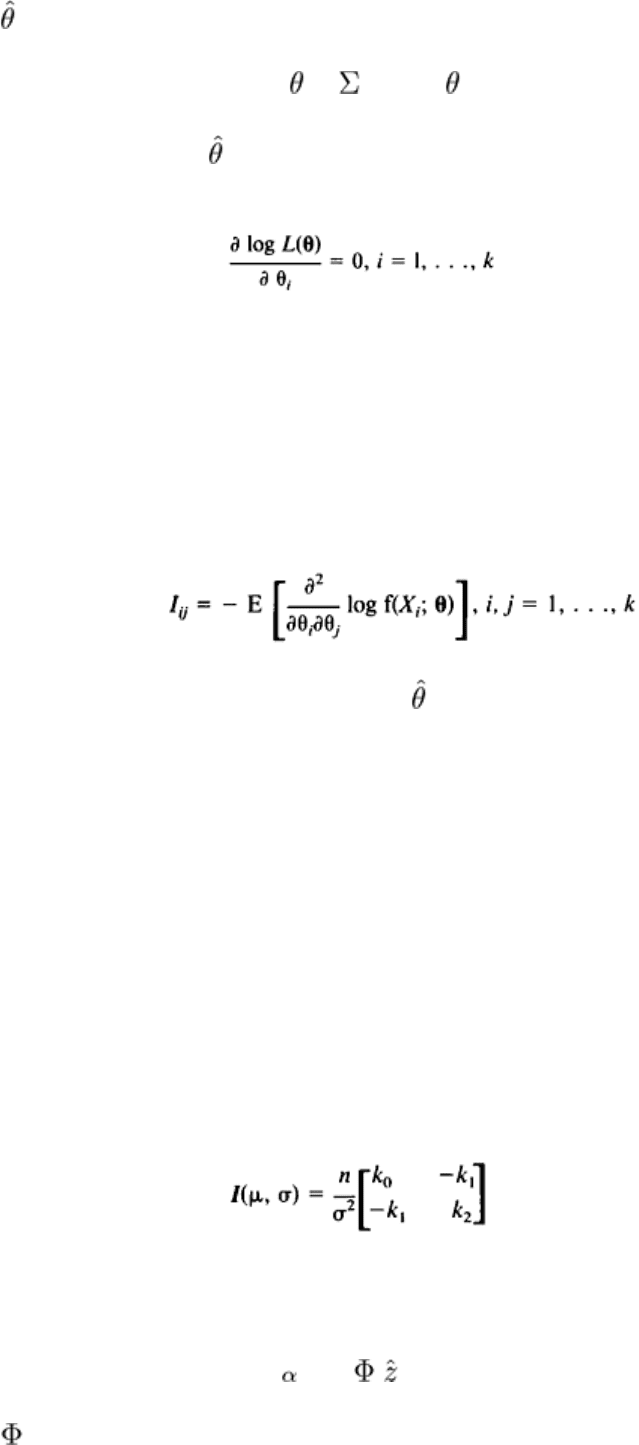
For a given outcome of the experiment, X

is known and Eq 17 is a function of θ. The maximum likelihood estimate is the

value, , which maximizes L(θ). For the models considered here, it is more convenient to work with the log L(θ):

log L( ) = log f(X

; )

(Eq 18)

which is also maximized at . The maximum likelihood estimates are given by the solution of the k simultaneous

equations:

(Eq 19)

Asymptotic Sampling Distribution Properties. For the models being used in NDE reliability studies, the

maximum likelihood estimates are invariant, consistent, and efficient. Further, they are asymptotically joint normally

distributed with means given by the true parameter values, θ

, and the variance-covariance matrix defined by:

V = I

-1

(Eq 20)

where I is the information matrix whose elements I

are the expected (E) values:

(Eq 21)

In application, the maximum likelihood estimate, , is substituted for θ in Eq 21. Therefore, given the results of

inspecting a large number of flaws and a specific function for the POD(a) model, the parameters of the model can be

estimated, and the sampling distribution of the parameters will be joint normal with the known variance-covariance

matrix. Examples of these equations for the hit/miss and response signal models are given in the sections "Analysis of

Hit/Miss Data" and "Signal Response Analysis," respectively, in this article. In these applications, the assumed models

will be the log odds and cumulative log normal distribution functions. However, other models can also be used if

evidence is available to support their selection.

Confidence Bounds on the POD(a) Function. Because the POD(a) function is equivalent to a cumulative

distribution function and the parameters are being estimated by maximum likelihood, a procedure developed by Cheng

and Iles (Ref 12 and 13) can be used to place lower confidence bounds on the POD(a) function. Such bounds are

calculated from the variance-covariance matrix of the estimates and reflect the sensitivity of the experiment to both the

number and sizes of flaws in the specimens of the experiment.

The assumed POD(a) model is a cumulative log normal distribution function with parameters θ= (μ,σ)'. For distribution

functions defined by location and scale parameters (as is the case of the log normal distribution), the information matrix

can be written in the form:

(Eq 22)

where n is the number of cracks in the experiment. The lower one-sided confidence bound of the POD(a) function is

given by:

POD (a) = ( - h)

(Eq 23)

where (z) is the standard cumulative normal distribution, and:

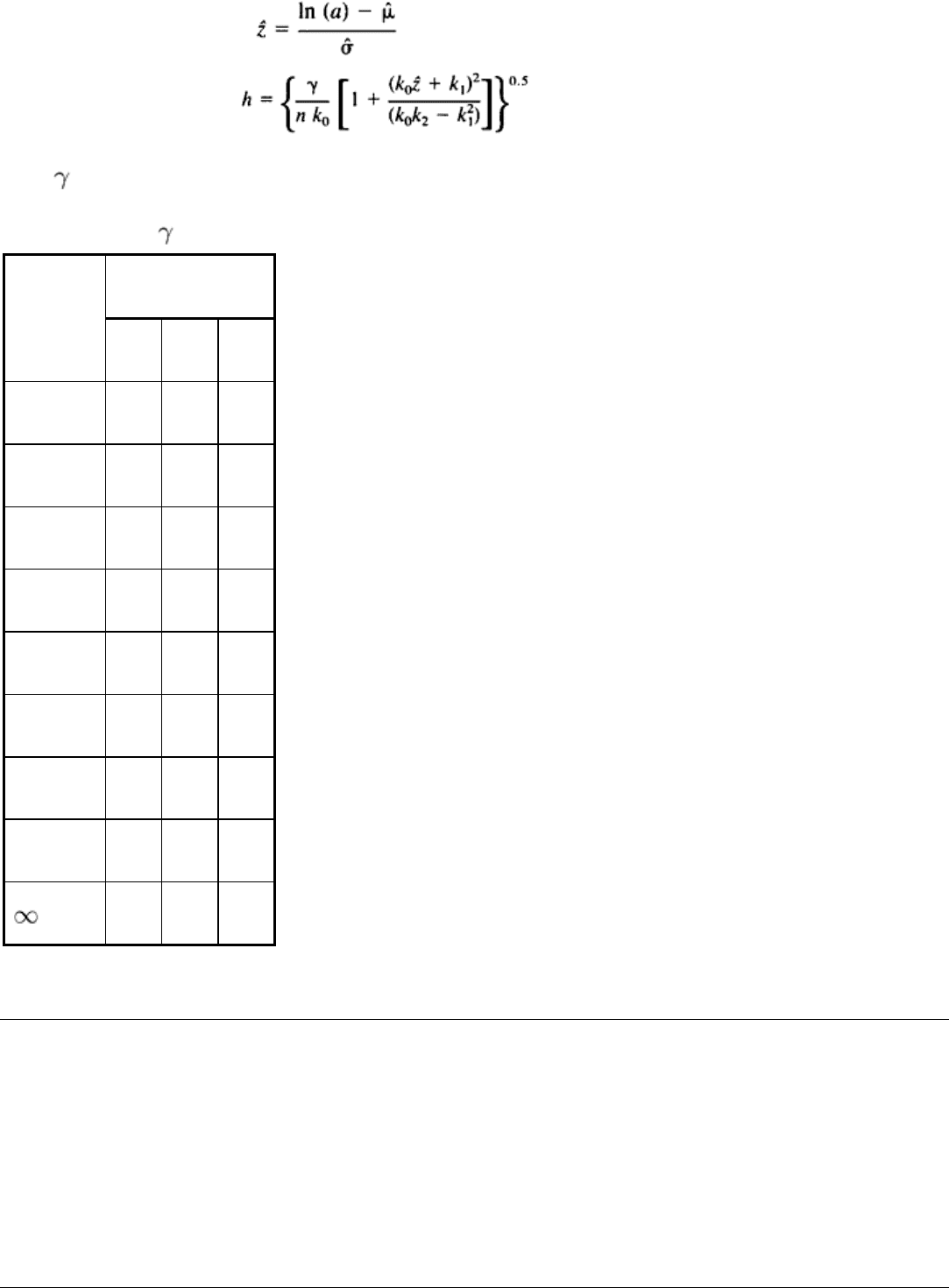
(Eq 24)

(Eq 25)

where is obtained from Table 3 for the number of cracks in the experiment and the desired confidence level.

Table 3 Values of for lower confidence bounds on the POD(a) function

Confidence level, %

Sample size

90 95

20 3.903

5.243

8.401

25 3.884

5.222

8.376

30 3.871

5.208

8.359

40 3.855

5.191

8.338

50 3.846

5.180

8.325

60 3.839

5.173

8.317

80 3.831

5.165

8.306

100 3.827

5.159

8.300

3.808

5.138

8.273

References cited in this section

10.

H. Cramer, Mathematical Methods of Statistics, Princeton University Press, 1946

11.

J.F. Lawless, Statistical Models and Methods for Lifetime Data, John Wiley & Sons, 1982

12.

R.C.H. Cheng and T.C. Iles, Confidence Bands for Cumulative Distribution Functions of Continuous

Random Variables, Technometrics, Vol 25 (No. 1), Feb 1983, p 77-86

13.

R.C.H. Che

ng and T.C. Iles, One Sided Confidence Bands for Cumulative Distribution Functions,

Technometrics, Vol 32 (No. 2), May 1988, p 155-159

NDE Reliability Data Analysis

Alan P. Berens, University of Dayton Research Institute

Analysis of Hit/Miss Data

Estimation of the parameters of the log odds model for hit/miss data is based directly on the probability of each 0 or 1

result of an inspection. Assume that a balanced experiment has produced k inspections on each of n cracks. For this

application, the likelihood function is given by:

(Eq 26)

where Z

= 0 or 1 for the jth inspection of the ith flaw producing a miss or a find, respectively, and the probability of

detecting a flaw of size a

is given by:

(Eq 27)

(Eq 28)

This form of the POD(a) function is simply a more convenient algebraic form of Eq 4. The vector of parameters to be

estimated is defined by θ= (μ,σ)'.

The log likelihood equation is:

(Eq 29)

Parameter Estimation in Hit/Miss Analysis. The maximum likelihood estimates are given by the solution to:

(Eq 30)

(Eq 31)

Taking the derivatives and simplifying yields:

(Eq 32)

(Eq 33)

Any standard computational method, such as the Newton-Rhapson iterative procedure (Ref 14), can be used to find the

solutions to Eq 32 and 33.

Because iterative techniques converge to local maxima, the solution to Eq 32 and 33 may be sensitive to the initial values.

A set of initial values based on the method of moments has been found to be useful (Ref 7). These are given by:

(Eq 34)

(Eq 35)

where X

,. . .,X

are the ordered values of the natural logs of the flaw sizes and p

is the observed percentage of detections

of the ith ordered flaw size. If convergence is not obtained, increasing the initial estimate of a has often provided

convergence. However, Eq 32 and 33 are not always solvable. This will be discussed further in the section "Comments on

Hit/Miss Analysis" in this article.

Confidence Bound Calculation in Hit/Miss Analysis. The information matrix is estimated from Eq 21, using

and for and . For this POD(a) model, the elements of the information matrix are given by:

(Eq 36)

(Eq 37)

(Eq 38)

Note that k

, k

, and k

, the parameters required in the calculation of the lower confidence bound on the POD(a) function,

are also defined by Eq 36, 37, and 38. All of the parameters required by Eq 23, 24, and 25 to calculate the lower

confidence bound on the POD(a) function are available.

Hit/Miss Analysis Examples. As examples of the application of the method to real data, the parameters of the log

odds POD(a) function were obtained for the data in Table 1. Table 4 presents a summary of the parameters of the POD(a)

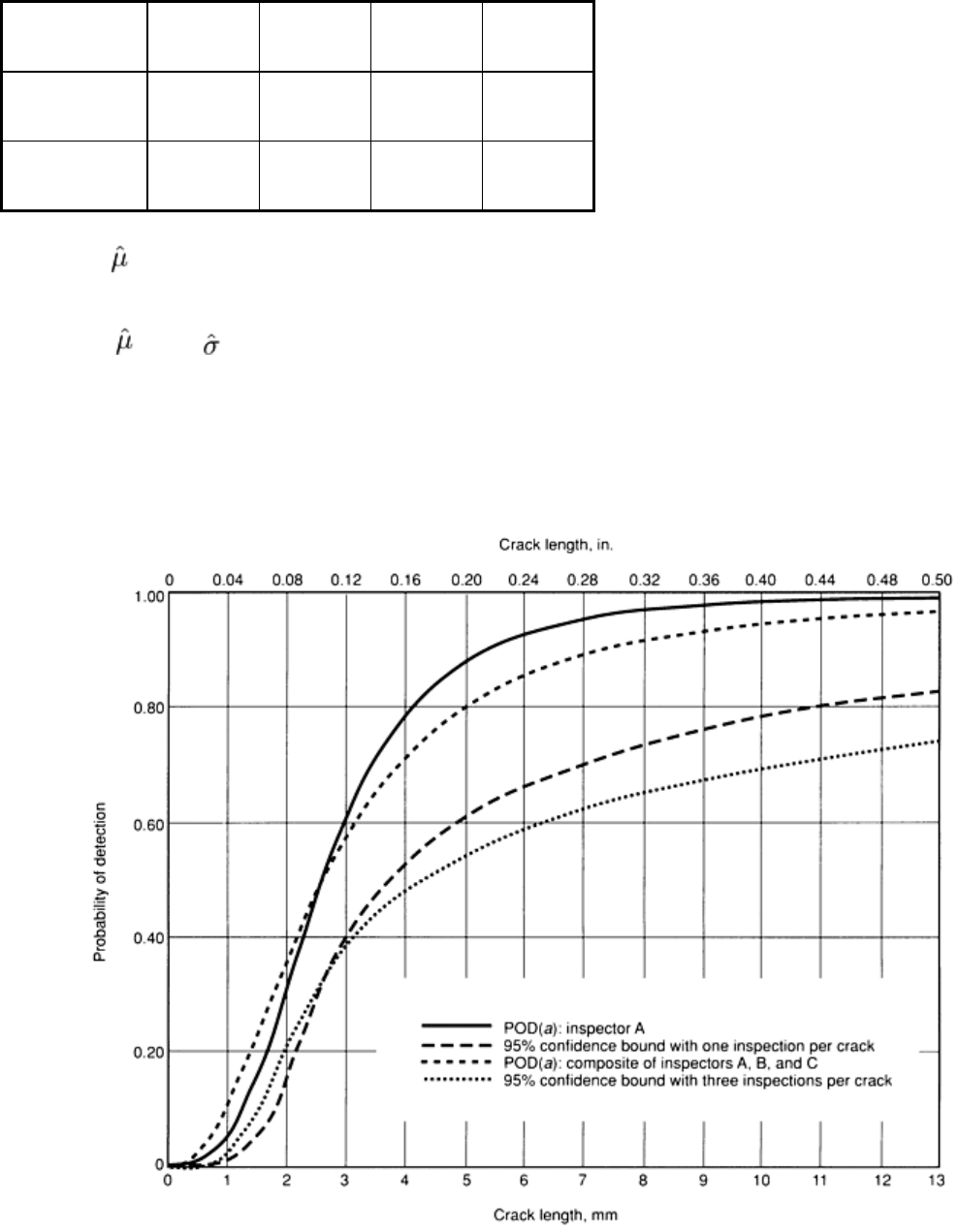
function for each data set of Table 1 and the combination of the three data sets in a single analysis. Figure 7 shows the

POD(a) function and the lower 95% confidence bound for Inspector A and the same information when the data from the

three inspectors are combined. Adding inspections of the same cracks did not increase the precision of the estimate of the

POD(a) function. Figure 8 compares the POD(a) functions for the three inspectors and the composite.

Table 4 POD(a) parameters for the hit/miss data in Table 1

Inspector Parameter

A B C

Composite

0.96 1.11 0.82

0.96

0.59 1.04 0.87

0.88

, mm (in.)

(a)

2.62 (0.103)

3.03 (0.119)

2.27 (0.089)

2.61 (0.103)

, mm (in.)

(b)

5.34 (0.210)

10.6 (0.417)

6.54 (0.257)

7.18 (0.283)

90/95

, mm (in.)

(c)

21.6 (0.850)

232 (9.13) 38.8 (1.53) 51.0 (2.01)

(a)

= exp( ) = estimate of crack size at 50% POD.

(b)

= exp( + 1.282 ) = estimate of crack size at

90% POD.

(c)

90/95

= upper 95% confidence bound on the estimate

of a

Fig. 7 POD(a) function and lower 95% confidence bound from hit/miss analysis of the data in Table 1

for one

insp

ection per crack (from Inspector A) and for three inspections per crack (from the composite result of

Inspectors A, B, and C)

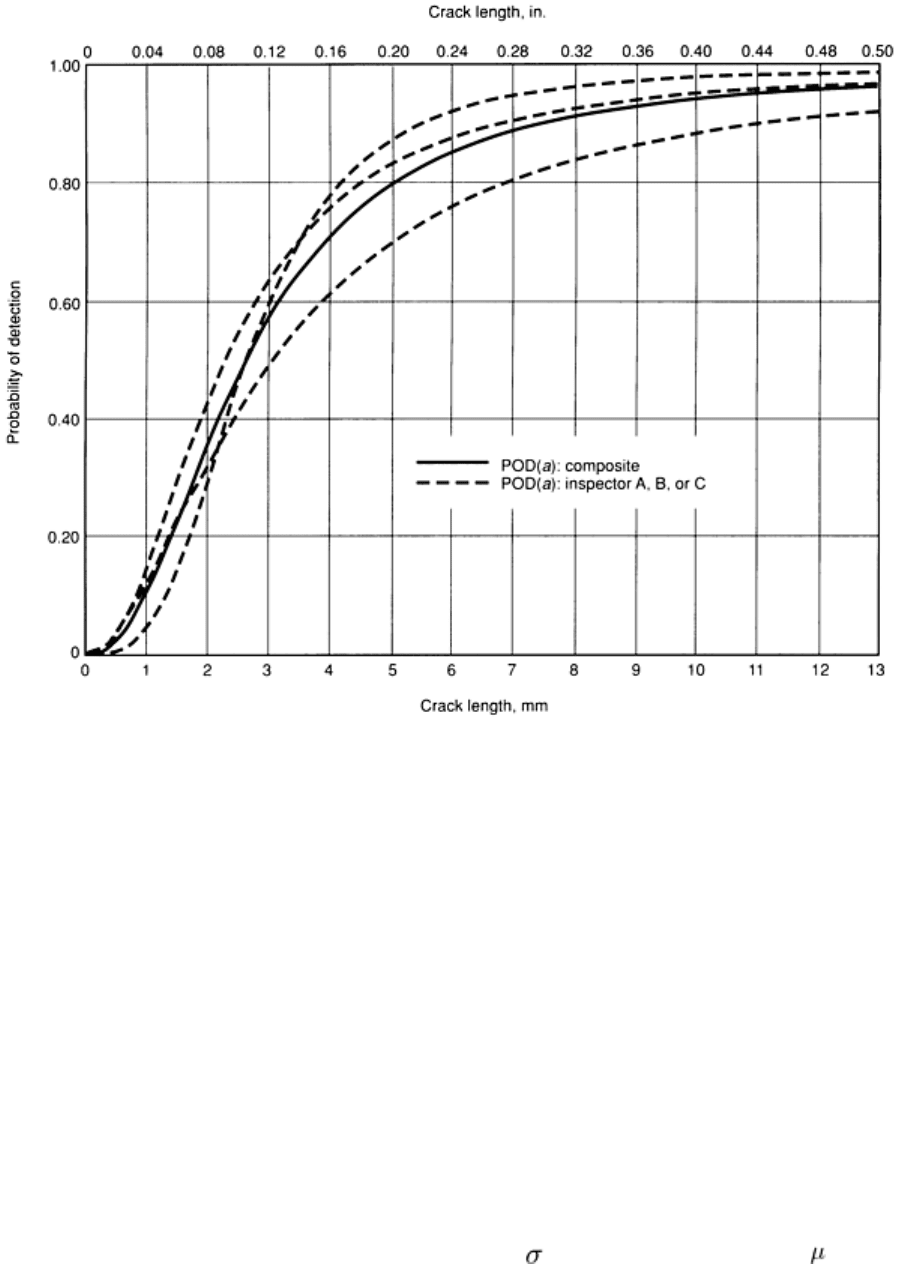
Fig. 8 POD(a) functions from hit/miss analysis of the data in Table 1

Comments on Hit/Miss Analysis. In a well-designed experiment of sufficient sample size for which the log odds

model is a reasonable representation of the POD(a) function, the maximum likelihood hit/miss analysis will provide a

valid solution. Conversely, lacking any of these elements, it is possible that either no solution or an unacceptable solution

can result. If there is no overlap in the flaw size ranges of the detections and misses, Eq 32 and 33 will not yield a

solution. More flaws are needed in the region of increase of the POD(a) function. It is also possible to obtain an estimate

of a POD(a) function that decreases with flaw size if the inspection system is poorly designed or not in control and if

large flaws tend to be missed more often than small flaws. Both of these types of results are readily apparent, albeit

disconcerting.

A third type of unacceptable result is an apparently acceptable POD(a) function but a confidence bound that eventually

decreases with flaw size. This situation is most easily understood in terms of the log odds versus log flaw size plot. If the

slope is positive, the POD(a) function will appear reasonable, but if it is not significantly greater than zero, the lower

confidence bound will eventually decrease with flaw size. Therefore, a decreasing confidence bound is evidence of lack

of fit of the log odds model.

Finally, lack of fit of the model is often manifest in large values of coupled with small values of or extremely wide

confidence intervals. Although there are, in general, insufficient data in hit/miss experiments to test hypotheses about the

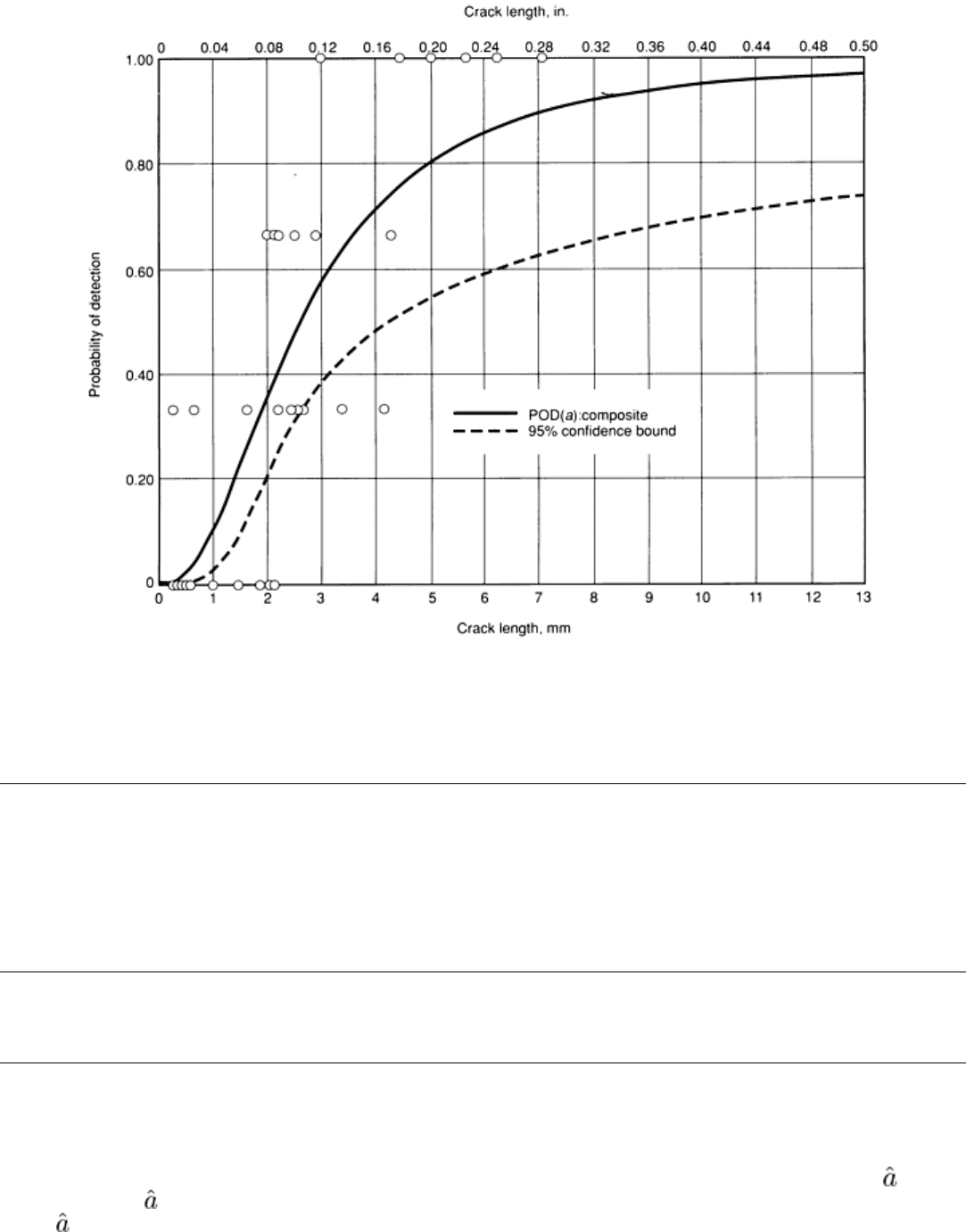
POD(a) model, as a minimum each fit should be subjectively judged. For example, in Fig. 9, the observed detection

proportions of each crack in the data of Table 1 are superimposed on the composite POD(a) function and confidence limit

from Fig. 7. The uncertainty in the POD(a) function as indicated by the width of the confidence bound seems justified by

the plot of the raw data. In this example, if greater precision (narrower confidence bounds) were desired, more cracks in

the 2 to 8 mm (0.08 to 0.3 in.) range would be needed in the experiment. Such plots provide an indication of the fit of the

model to the data as well as the range of flaw sizes that are contributing to the information from which the POD(a)

function is being estimated. This is true even for experiments in which there is only one inspection per crack and all

detection probabilities are plotted at 0 or 1.

Fig. 9 Example fit of hit/miss POD(a) function and lower 95% confidence bound

to observed detection

probabilities (three inspections per crack)

References cited in this section

7. A.P. Berens and P.W. Hovey, "Flaw Detection Reliability Criteria, Volume I--

Methods and Results,"

AFWAL-TR-84-4022, Air Force Wright-Aeronautical Laboratories, Wright-

Patterson Air Force Base, April

1984

14.

A. Ralston, A First Course in Numerical Analysis, McGraw-Hill, 1965

NDE Reliability Data Analysis

Alan P. Berens, University of Dayton Research Institute

Signal Response Analysis

In signal response data analysis, the parameters of the POD(a) function are calculated from parameters of the versus a

relation. If all the values are between the signal recording threshold and the saturation limit, a simple regression analysis

of ln ( ) versus ln (a) will yield the necessary information to estimate the POD(a) function and its lower confidence