ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control
Подождите немного. Документ загружается.

components would ideally take advantage of analytical or numerical computations to model the expected lifetime
performance of a component. At present, extensive capabilities are in place for modeling stresses and failures, and these
are widely used in the design process. However, the modeling of nondestructive evaluation is not nearly as widely
accepted. Instead, frequent use is made of empirical rules based on extensive demonstration programs. For both economic
and time reasons, there is a significant need to develop a model base for estimating NDE reliability (which is often
measured in terms of the probability of flaw detection at given confidence level). It is the purpose of this article to present
the current status and future directions of efforts to develop such a capability. This is not intended as a review of
international efforts in NDE reliability modeling but rather as a summary of the authors' experience in modeling the
inspectability of aerospace components, with emphasis on engine components. Therefore, attention is given to ultrasonic,
eddy current, and radiographic inspection. Broader sets of references for the case of ultrasonics can be found in recent
review articles (Ref 2, 3). Of particular note is the work performed by the Central Electricity Generating Board in
modeling the inspectability of nuclear power generating components (Ref 4).
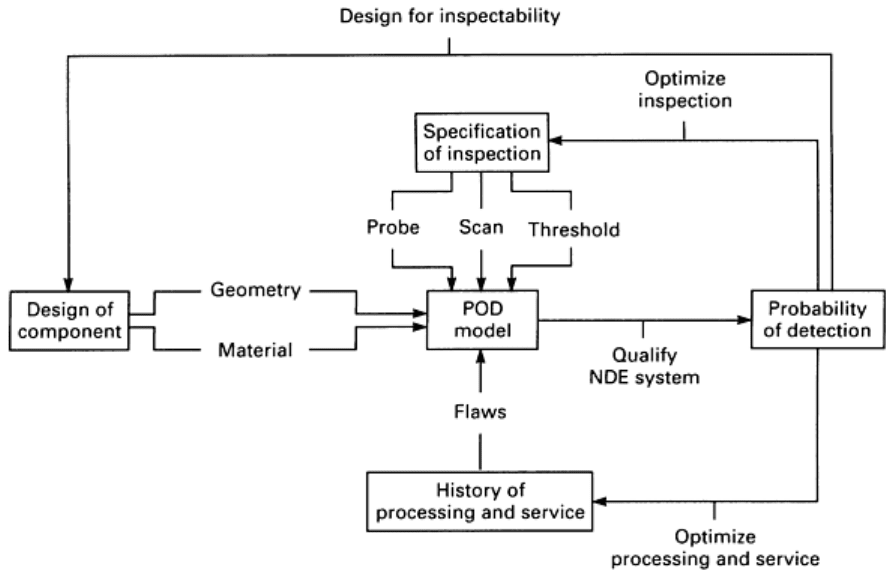
The details of models for NDE reliability are partially dictated by their envisioned uses (Ref 5, 6), which are conceptually
illustrated in Fig. 2. One would like to have a model that predicts the probability of detecting flaws of various sizes. This
would clearly require as inputs the design of the component, its history of processing and service, and a specification of
the inspecting methodology to be used. Given the specifications of these input parameters, it could first be asked whether
the predicted probability of flaw detection of the NDE system is adequate to meet the demands imposed by the required
performance of the component. Should the expected probability of detection (POD) be inadequate, the model could be
exercised to modify the specifications of the inspection, the design of the component, or the processing or service profiles.
The NDE models thus become an integral part of a broader concept known as unified life cycle engineering or
simultaneous engineering (Ref 7). The essential feature is that one should consider all aspects of the life of a component
in the design process, including the ability to inspect and maintain the component, rather than just the initial costs. This
will ultimately lead to more sophisticated networking of models, as shown in Fig. 3. Figure 3 illustrates a number of
factors that must be added to the traditional computer-aided design and manufacturing (CAD/CAM) methodologies to
produce a design optimized for life cycle performance. Multiple interactions among the various factors must be
considered to allow the design to address simultaneously all the issues associated with damage tolerance (Ref 8).
Fig. 2
Diagram of probability of detection model and its application to NDE system qualification and
optimization and to computer-aided design for inspectability. POD, probability of detection
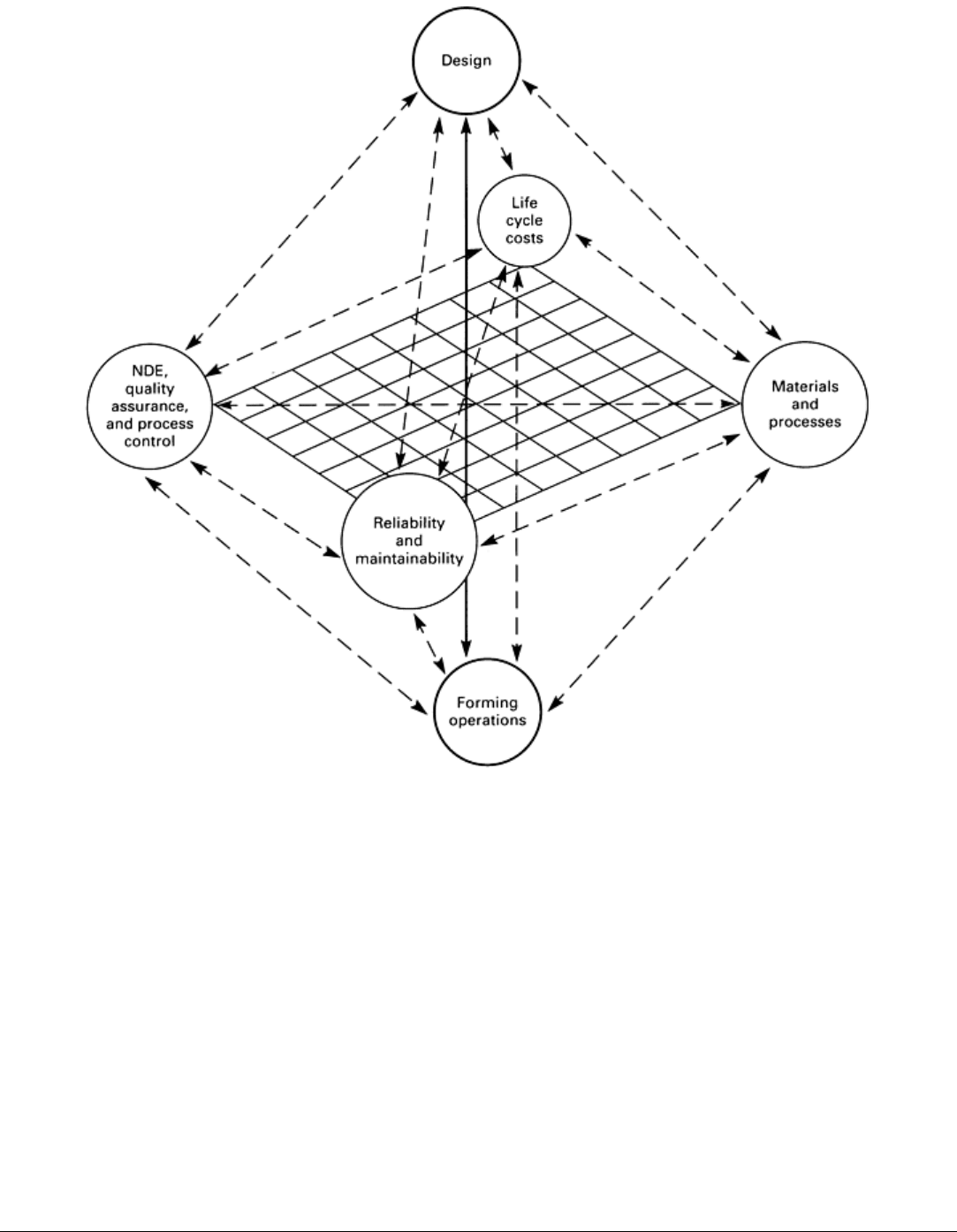
Fig. 3 Schematic of possible linkages needed for unified life cycle engineering
Given these objectives, it is obvious that an NDE model must exhibit certain characteristics. First, it must predict the
response of a real measurement system, as influenced by the specific characteristics of commercially available probes and
instruments, rather than an idealized response based on assumptions such as plane wave illumination. Second, the models
should give as outputs the information obtained by real inspection protocols. For example, if a signal strength is compared
to a threshold as a criterion for detection, this operation should be simulated by the model. If separate protocols are
followed in detection and sizing, these should be described by separate models. Third, the models should be used to
develop more reliable standardization approaches. This is necessary to ensure that inspections specified in the design
process are uniformly implemented by NDE units at the various manufacturing and maintenance departments encountered
by the component in its lifetime. Fourth, it is desirable in certain industries for the models to be configured such that they
can be integrated with standard CAD packages. This article discusses some ultrasonic, eddy current, and x-ray
radiography models that have been developed to exhibit the characteristics mentioned above. As noted previously,
primary emphasis is placed on formulations that have been developed in response to the particular needs of the aerospace
industry. This article also presents a broader discussion of possible future applications of a reliability modeling capability.
References
1.
S.T. Rolfe and J.M. Barson, Fracture and Fatigue Control in Structures: Application of Fracture Mechanics,

Prentice-Hall, 1977
2.
R.B. Thompson and T.A. Gray, Use of Ultrasonic Models in the Design and Validation of New NDE
Techniques, Philos. Trans. R. Soc. (London) A, Vol 320, 1986, p 329-340
3.
R.B. Thompson and H.N.G. Wadley, The Use of Elastic Wave-
Material Structure Interaction Theories in
NDE Modeling, CRC Crit. Rev. Solid State Mater. Sci., in press
4.
J.M. Coffey and R.K. Chapman, Applica
tion of Elastic Scattering Theory for Smooth Flat Cracks to the
Quantitative Prediction of Ultrasonic Defect Detection and Sizing, Nucl. Energy, Vol 22, 1983, p 319-333
5.
R.B. Thompson, D.O. Thompson, H.M. Burte, and D.E. Chimenti, Use of Field-Flaw Inte
raction Theories to
Quantify and Improve Inspection Reliability, in
Review of Progress in Quantitative Nondestructive
Evaluation, Vol 3A, D.O. Thompson and D.E. Chimenti, Ed., Plenum Press, 1984, p 13-29
6.
T.A. Gray and R.B. Thompson, Use of Models to Predict Ultrasonic NDE Reliability, in
Review of Progress
in Quantitative Nondestructive Evaluation,
Vol 5, D.O. Thompson and D.E. Chimenti, Ed., Plenum Press,
1986, p 911
7.
H.M. Burte and D.E. Chimenti, Unified Life Cycle Engineering: An Emerging Design Concept, in
Review of
Progress in Quantitative Nondestructive Evaluation,
Vol 6B, D.O. Thompson and D.E. Chimenti, Ed.,
Plenum Press, 1987, p 1797-1809
8.
D.O. Thompson and T.A. Gray, The Role of NDE in Global Strategies for Materials Synthesis and
Manufacturing, Proceedings of the 1988 Fall Meeting, Materials Research Society, in press
Models for Predicting NDE Reliability
J.N. Gray, T.A. Gray, N. Nakagawa, and R.B. Thompson, Center for NDE, Iowa State University
Ultrasonic Inspection Model
Empirical determinations of ultrasonic inspectability based on demonstration experiments are of limited utility because
their predictions cannot, in general, be extrapolated to new situations beyond the bounds of the data set upon which they
are based. Additional data are needed in order to apply them to other cases, and the costs and time required to develop
such results for all (or many) possible component designs and scan plans are prohibitive. However, the physical principles
upon which many different ultrasonic inspection techniques are based, as applied to a variety of components, are quite
similar. Therefore, a mathematical model, whose validity has been proved against a relatively small amount of empirical
data, can be used to accurately predict inspectability beyond the bounds of the experimental evidence.
The foundation of a physically based mathematical or computer model of ultrasonic inspectability is an analytical
formalism, a numerical algorithm, or a combination of the two incorporating the physical principles of the measurement.
Such a model consists of descriptions of the waves radiated by the probes, their modification by the geometry of the
testpiece, the wave propagation and scattering from defects, and the effects of signal processing and display. The first four
sections below review the technical details of each of these elements as developed to describe measurements made in
aircraft engine components.
In the fifth section, the use of the models to predict the POD of flaws is discussed. The prediction of the POD for flaws is
emphasized because of the importance of that parameter in damage-tolerant design. Other uses of models, such as
assisting in the interpretation of data during flaw characterization and sizing, are also important but are not explicitly
discussed. Some early applications of POD models are summarized in the sixth section.
Reciprocity Relation. The ultrasonic NDE simulation models described in this section are based on the formalism of
the electromechanical reciprocity relationship of Auld (Ref 9). This relationship, when specialized to the case of elastic
wave scattering, can be expressed as follows. Assume that two identical ultrasonic transducers, a and b, are placed in a
fluid to be used in an immersion, pitch-catch measurement (a single probe, or pulse-echo, configuration is a special case)
of a component containing a flaw, F. Let be the ratio of the electrical signal radiated into coaxial line b by the receiving
transducer to the electrical signal incident on the transmitting probe from coaxial line a. Then the change,
F
, in this
signal induced by the presence of the flaw in the insonified region of the component is given by:

(Eq 1)
where
a
and
a
are the displacement vector field and the stress tensor, respectively, that would be produced in the
presence of the flaw when probe a is excited by an electrical power P,
b
and
b
are the fields that would have been
established in the absence of the flaw if probe b had been excited, the overhead dot denotes time differentiation, S
F
is an
arbitrary closed surface enclosing the flaw, and n is the inward normal to that surface. Equation 1 is an exact result known
as the electromechanical reciprocity relationship. Its simplicity, however, belies its intractability, except in a very few
special cases of limited practical use.
Measurement Model. A number of approximations and simplifications are necessary in deriving an accurate yet
computationally efficient inspection measurement model from Eq 1. One situation for which a useful and accurate model
can be extracted from Eq 1 through rather remarkable simplifications is the pulse-echo inspection of isotropic,
homogeneous elastic materials containing small flaws of fairly simple shape. This is applicable, for example, to typical
ultrasonic inspections of gas turbine aircraft engine components, in which fracture-critical flaws are quite small because
of the high stresses created during engine operation.
The assumption of small in this case means that the dimensions of the defect are small relative to the variations in the
transverse profile of the ultrasonic beam. The ultrasonic fields can be approximated locally as plane waves whose
displacement and stress fields are the same as those of the true fields (Ref 10). Scattered fields can also be simply
modeled, provided their variation is not significant over the face of the receiving transducer. These fields can be
represented by the product of a spherically spreading wave times the far-field, unbounded medium scattering amplitude of
the flaw (Ref 10). This scattering amplitude A is formally defined as:
(Eq 2)
where u
s
is the displacement amplitude of the fields at a distance r from the center of the flaw, u
0
is the amplitude of an
illuminating plane wave, and k
s
is the wavenumber of the scattered wave mode. A time-harmonic term of the form exp
(i t) is implicitly assumed in this discussion. However, the model has the capacity to deal with pulses, as described later.
Applying these approximations to Eq 1, the a fields (those produced when probe a is fired and the flaw is present) are
expressed as the sum of a plane wave illuminating field and a scattered field due to that plane wave, using the scattering
amplitude as in Eq 2. The b field is simply a plane wave term representing illumination by probe b in the absence of the
flaw. After some manipulation of the resulting integral and neglecting higher-order terms, a measurement model is
derived that represents the measured signal as a product of factors describing the effects of transducer efficiency,
transmission through interfaces, attenuation and beam spread, and scattering (Ref 10). Specifically, one finds:
(Eq 3)
where β is an efficiency factor; T
a
C
a
and T
b
C
b
represent local plane wave amplitudes at the flaw depth for the a and b
fields (these are the product of interface transmission, T, and beam diffraction, C, factors); A is the scattering amplitude of
the flaw; ρ
1
V
b
and ρ
0
V
0
are the acoustic impedances of the solid and fluid media, respectively; k
b
is the wavenumber for
the received wave mode; a
T
is the transducer radius (which is assumed to be the same for both a and b); and the two
exponential terms represent the ultrasonic phase change and attenuation, respectively. Equation 3 represents only one
frequency. A frequency spectrum can be obtained via superposition of individual frequency terms. Thus, time-domain
waveforms, such as would be observed on an oscilloscope screen, can be obtained by an inverse Fourier transform of this
measurement model spectrum. (Further details of this derivation and the determination of the efficiency factor in Eq 3
can be found in Ref 10.) Work at a number of institutions has led to formulas, algorithms, and data bases for the
ultrasonic beam and scattering amplitude factors in Eq 3, so that a variety of useful simulations can be made, including
the use of planar or focused probes (Ref 11, 12, 13, and 14), inspection through planar or curved liquid/solid interfaces
(Ref 11, 12, 14, and 15), and scattering from both volumetric (Ref 16, 17, 18) and cracklike (Ref 17, 19) defects. These
aspects of the measurement model will be described in subsequent sections in this article. An alternative formulation,
appropriate when the flaw is not small, is found in Ref 4.
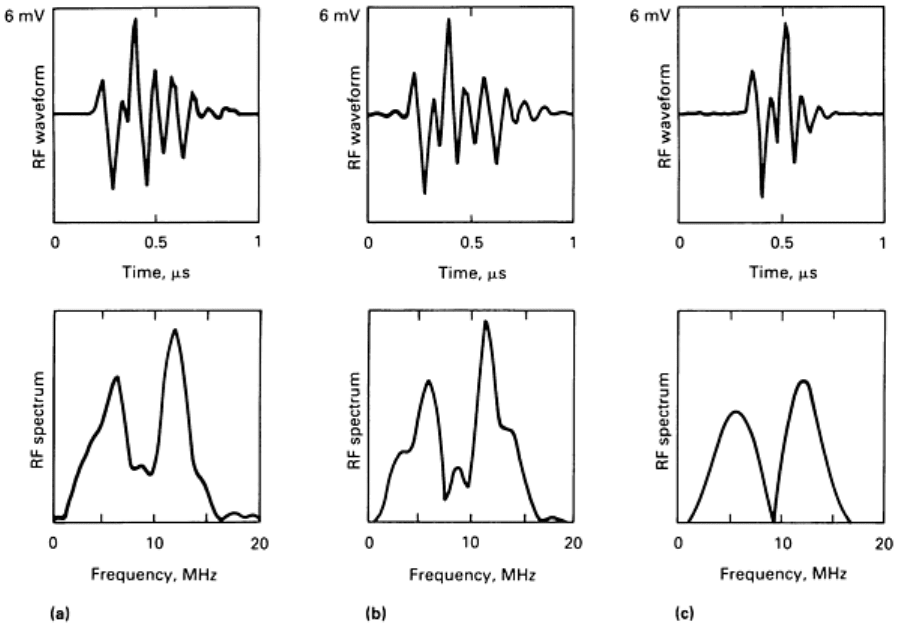
As an example, Fig. 4 shows a comparison of an experimental pulse-echo radio-frequency (RF) waveform obtained from
a circular flat crack versus two model-based simulations. The magnitude of the Fourier spectrum of each RF signal is also
shown. The simulated crack was a circular, disk-shaped cavity 0.8 mm (0.032 in.) in diameter and 0.08 mm (0.003 in.)
thick located in a diffusion bond plane of a specimen of a nickel-base powder metal alloy (IN 100). The specimen was a
25 mm (1.0 in.) thick plate. The face of the crack was parallel to the surface of the sample, and a 10-MHz, 6.35 mm (0.25
in.) diam unfocused transducer was tilted approximately 7° from normal to the sample surface to generate a 30° refracted
longitudinal wave in the sample.
Fig. 4 Comparisons between experimental and model-
predicted RF waveforms (top) and their Fourier spectra
(bottom) for 30° longitudinal wave backs
catter from a 0.8 mm (0.03 in.) diam circular crack in IN100. (a)
Experimental measurements of scattering amplitudes (top) and their Fourier spectra (bottom). (b) Model of
scattering with method of optimal truncation. (c) Model of scattering with the Kirchhoff approximation
The scattering amplitudes used in Fig. 4 were either results of the method of optimal truncation (MOOT) (Ref 17), which
is a computationally intensive algorithm, or the elastodynamic Kirchhoff approximation (Ref 19). The experimental and
MOOT results are very nearly identical in both the time and frequency domains. Because the MOOT results are in quasi-
exact agreement with the measured scattering amplitudes in this case, this comparison highlights the accuracy of the
measurement model. The Kirchhoff model result fails to reproduce some of the detailed wiggles of the experimental and
MOOT results, but quite accurately reproduces the overall signal amplitude (voltage). This amplitude is the measured
quantity that is routinely used in ultrasonic flaw detectors. Therefore, the approximation, which in this case yields a
simple and computationally efficient model, can simulate a practical inspection problem. Note, however, that the error of
the Kirchhoff model will depend on the flaw size and the orientation and polarization of the ultrasonic wave. Care must
be taken to ensure that sufficient accuracy is obtained in particular applications by validating the model through
comparison with controlled experiments and/or more exact theories for special cases.
Beam Models. To perform the preceding comparison, one essential element in the simulation was the representation of
the ultrasonic fields in the vicinity of the flaw. Because of the finite size of any realistic transducer, these fields will be
quite complex, exhibiting peaks and valleys along the axis of the beam and side-lobes away from the axis. The
simulations shown in Fig. 4 represent the case of a scatterer on the axis of the beam, for which a number of approximate
beam models have been generated (Ref 11, 13, 14). In a typical automated ultrasonic scan of a component, however, a
defect in that component will not generally lie along the axis of the ultrasonic beam. The degree of misalignment will
depend, for example, on the coarseness of the scan mesh used to inspect the part. To simulate such an inspection situation,
it is necessary to incorporate the full fields of an ultrasonic transducer into the model. This is a formidable task because of
the elastic (tensor) nature of wave propagation in a solid and because of the need to consider the interaction of the probing
fields with a possibly curved liquid/solid interface at the component surface. However, two approximations have emerged
as useful models of transducer radiation patterns: the Gaussian model (Ref 12) and the Gaussian-Hermite model (Ref 13,
14, 20).
The former, and simpler, of these models assumes that the transverse profile of the radiation profile is Gaussian in shape
at all distances from the probe. This Gaussian beam model provides a set of simple algebraic formulas that predict
diffraction effects (beam spread only), effects of lenses, and refraction/focusing due to transmission through curved
liquid/solid interfaces (Ref 12). However, typical ultrasonic transducers do not generate Gaussian radiation patterns. For
example, typical piston-type radiators exhibit side-lobes and peaks and nulls along the axis of the probe in the near field.
However, in the far field (that is, several times the near-field distance), the Gaussian model, if suitably normalized, does
accurately predict the amplitude and width of the main lobe in the radiation pattern of a typical piston-type transducer
(Ref 12). One application of this approximation, therefore, is the simulation of the fields near a focal region, which can
occur either as a result of an acoustic lens on the probe or the focusing effect of a curved component surface.
The Gaussian-Hermite model is based on a series expansion of the radiated fields of a transducer in terms of a complete
set of orthogonal solutions to a reduced wave equation (Ref 13, 14, 20). These functions are products of a Gaussian factor
and a Hermite polynomial. The coefficients in the series expansion are obtained by integrating the product of the
Gaussian-Hermite functions and the velocity distribution on the face of a probe over its area. This distribution and the
shape of the probe face are arbitrary, so that virtually any probe shape, lens type, and so on, can be modeled. The laws for
transmission through curved liquid/solid interfaces and propagation in elastic isotropic media are implemented as simple
algebraic operations. The primary disadvantage of the Gaussian-Hermite model is that it is a series solution and therefore
can require significantly longer computation times than the Gaussian approximation because of the need for a large
number of terms, especially in the near field. However, this becomes less of a disadvantage as computational speeds
continue to increase as a result of advances in computer hardware.
Scattering Approximations. Another key element in the simulation of ultrasonic inspection of structures is the
model, or models, for representing the interaction of the probing ultrasonic fields with defects. In the most general case,
this is represented by a complicated and computationally intractable integral, such as Eq 1. In some cases, however, the
effects of the probing ultrasonic fields can be separated from the scattering effects. Specifically, under the assumptions
that led to the measurement model (Eq 3), the ultrasonic beam can be described by one of the models just mentioned. For
example, elastic wave scattering can be modeled through the use of a far field, unbounded medium scattering amplitude,
whose definition was given in Eq 2. Fortunately, considerable research effort has been directed over the past several years
toward the development of various models, approximations, and solutions for scattering amplitudes of both volumetric
and cracklike defects (Ref 3).
For application to the ultrasonic inspection of jet aircraft engine components, a reasonable inventory of scattering models
includes formalisms for both volumetric and cracklike flaws. For volumetric flaws, of ellipsoidal shape and arbitrary
orientation, both voids and inclusions can be represented by an elastodynamic Kirchhoff approximation (Ref 18). This
approximation is exact in its treatment of the strength of the front surface reflection ( function). It is valid for both
longitudinal and shear wave backscatter, such as would be used to simulate pulse-echo inspections. The limitation of this
model, however, is that it is accurate only for early-time events in the scattering. Therefore, it does not predict the
amplitude of scattered fields that have reverberated within an inclusion; in some cases, these scattered fields can be of
higher amplitude than the initial front surface reflection. The Kirchhoff approximation is therefore a conservative model
for scattering from volumetric flaws. It does have the benefit of simplicity and computational efficiency.
For cracklike flaws, an elastodynamic Kirchhoff approximation to scattering from internal flat cracks of elliptical shape
has been implemented for both pulse-echo and pitch-catch techniques and for longitudinal and shear wave modes (Ref
19). This Kirchhoff approximation accurately predicts the specular content (mirror reflection) of scattering, but does not
properly include edge diffraction contributions or surface wave modes. It also does not contain any provision for surface
roughness or partial closure of the crack faces. It does, however, yield reasonably accurate predictions of signal

amplitudes in the near-specular regime, as can be inferred from Fig. 4. One fairly significant limitation of the model is its
inaccuracy in the nonspecular regime. It predicts, for example, that the scattering amplitude is identically zero for edge-on
incidence from a crack, which is inconsistent with established crack scattering results (Ref 17, 21). However, the model is
of significant utility because an inspection system for detecting cracks would be set up to take advantage of specular
orientations, if possible. Furthermore, in this case, the Kirchhoff approximation is a simple and computationally fast
algorithm.
Probability of Detection Models. One important application of ultrasonic measurement modeling is the simulation
of probability of detection. Detection is appropriately described in terms of a probability for several reasons. A given size
and type of defect may occur at random positions and with a range of orientations within each of a set of nominally
identical components. The detailed shape of the defect may vary in a way that influences its ultrasonic response
differently from its fracture response. Variations in grains, porosity, surface roughness, and so on, as well as the electronic
equipment in a detection system, will cause noise, which will interfere with the signals from a flaw. Therefore, a given
size and type of defect will exhibit a distribution of signal amplitudes if measured in a population of components
containing such defects. Because these signal amplitudes are compared to a preset amplitude threshold in typical flaw
detectors, some of the flaws will be missed, while others will be detected. The POD is the ratio of the number of flaws
that are detected to the total number of flaws in the inspected components.
A formalism to predict the probability, p(S, N, T), that a given signal, S (video envelope), in the presence of noise with
total power N
2
will be detected by exceeding a threshold, T, is given by:
(Eq 4)
where i
o
(z) = exp (-z)I
0
(z), with I
0
(z) being the modified Bessel function of the first kind and order zero. This approach,
based on work performed by Rice (Ref 22), was developed for a narrow-band signal, as is typical in radar analysis.
Equation 4 represents only the probability of detecting a single signal level, S, and does not take into account the
distribution of signal amplitudes for variations in the size, shape, and type of flaw.
A POD model for ultrasonics has been developed by using the measurement model to calculate the variability of signal
levels as influenced by the position and orientation of the flaws. Then, for a given root-mean-square noise level, N, Eq 4
can be used to represent the probability that the video signal from a specific defect (a given size, shape, type, location,
orientation, and so on) in a given component (material, geometry, and so on) and using a specific inspection system will
exceed a threshold amplitude. As an example, let p
x
and p represent the probability distribution functions for the
location, x, and orientation, θ, of a given size, shape, and type of defect, and let S(x, θ) represent its signal amplitude, as
simulated by the measurement model. An expression for POD, assuming a noise level N and a detection threshold
amplitude T, can then be written formally as:
(Eq 5)
where the integrals are taken over the range of orientations and positions of possible flaws (Ref 15). Obvious
generalizations of Eq 5 can treat the effects of flaw shape, type, and so on.
Equation 5 does not contain an explicit factor to represent the probability distribution of the presence of flaws; therefore,
it predicts the probability that an ultrasonic indication (signal plus noise) will be detected assuming that a flaw is, in fact,
present. The use of the POD model to analyze reliability issues, such as the probabilities of falsely accepting flawed
components or of falsely rejecting good ones, would require the incorporation into the model of the probability
distribution function for flaws as a function of defect size, location within the part, and so on. The result of Eq 5 would
then need to be further integrated with respect to that probability distribution.
Applications. Figure 5 shows the results of simulating the detectability (POD) of circular cracks at three different
depths below a cylindrical component surface and for two different scan plans (Ref 6). Figure 5(a) illustrates the use of

the POD model to quantify the detection capability of an NDE system. For the specific parameters in that simulation,
cracks that are otherwise identical have significantly different detectability levels, depending on their depth below the
surface of the part. In this example, the curved surface of the component behaves like an acoustic lens that happens to
focus the beam at the middle depth (25 mm, or 1 in.). Because of the relatively coarse scan mesh and the reduced beam
width in this focal region, there is a significant likelihood that a flaw will be located in a low-amplitude portion of the
beam profile and, therefore not be detected. For the other two depths, the beam width is greater than the scan mesh
distance. The plot in Fig. 5(b) shows the result of sufficiently refining the scan mesh so that the beam width at the focal
region is greater than the distance between scan points. In this case, the POD curves are nearly the same for the three
different depths. This example illustrates the use of the POD model for quantifying the capability of a flaw detection
system and for suggesting improvements in this area in the system or its operation.
Fig. 5
Predicted influence of scan plan on POD. (a) POD at three depths for axial and circumferential scan
increments of 2.5 mm (0.1 in). (b) POD at three depths for axial and circumfere
ntial scan increments of 5 and
1.3 mm (0.2 and 0.05 in.), respectively
Another example of the use of the POD model is shown in Fig. 6 (Ref 6). The POD curve is expressed in a rather
nonstandard manner, because it does not represent the typical POD versus flaw size plot. Instead, Fig. 6 shows the
variation in POD due to modification of a geometrical parameter of a component. Specifically, the component is a
simulated turbine disk assumed to contain radially oriented circular cracks below a bicylindrical fillet. The abscissa of
Fig. 6 is the in-plane radius of curvature of that fillet. The flaw size is assumed to be constant, representing, for example,
the critical flaw size as predicted by fracture mechanics. Most important, Fig. 6 shows that flaw detectability can be
improved by modifying the geometry of the component. This information is important for the definition of sonic near-net
shapes of components in production, for example, and ensuring in-service inspectability during maintenance. Moreover,
because the characteristics of the inspection system are contained explicitly in the POD model, the scan plan required to
achieve the necessary detectability levels are easily determined. This concept of predicting component inspectability at
the design stage, of determining the component design parameters that favorably influence flaw detectability, and of
incorporating the requisite scan procedure into the design data base is perhaps the ultimate application of inspectability
modeling.
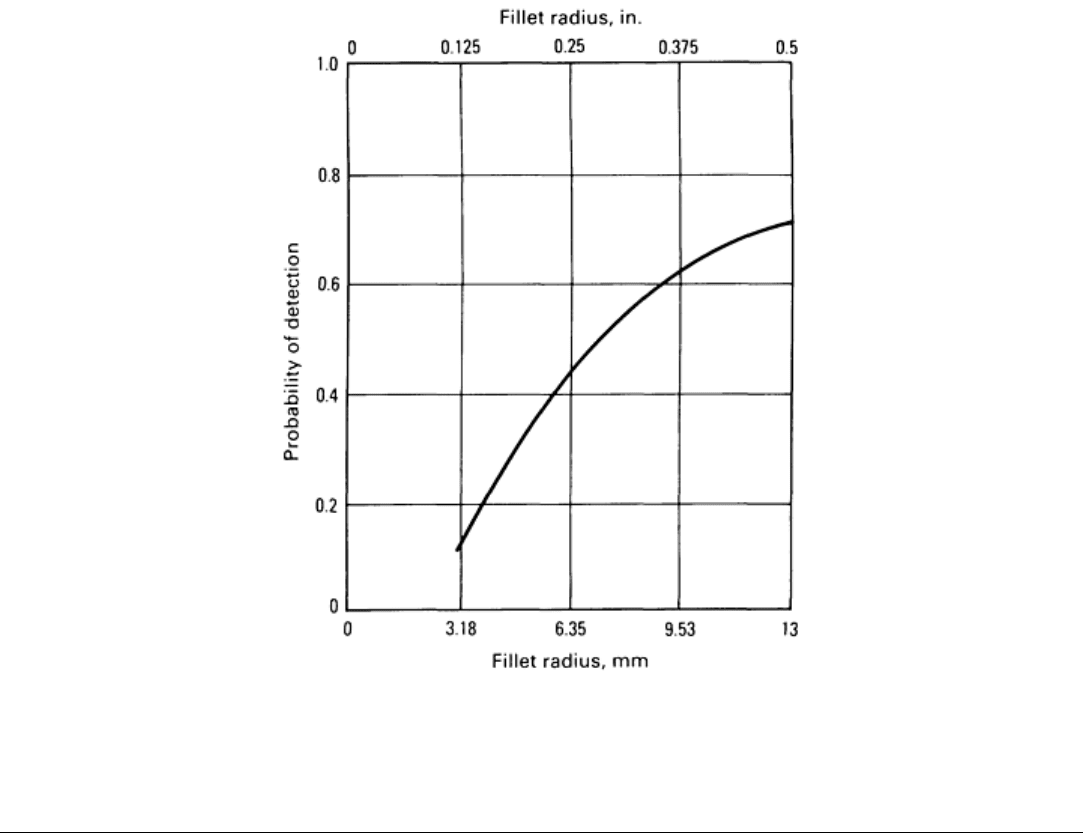
Fig. 6
Simulated POD for a 0.8 mm (0.03 in.) diam circular crack below a bicylindrical fillet as a function of fillet
radius of curvature
References cited in this section
3. R.B. Thompson and H.N.G. Wadley, The Use of Elastic Wave-
Material Structure Interaction Theories in
NDE Modeling, CRC Crit. Rev. Solid State Mater. Sci., in press
4.
J.M. Coffey and R.K. Chapman, Application of Elastic Scattering Theory for Smooth Flat Cracks to the
Quantitative Prediction of Ultrasonic Defect Detection and Sizing, Nucl. Energy, Vol 22, 1983, p 319-333
6. T.A. Gray and R.B. Thompson, Use of Models to Predict Ultrasonic NDE Reliability, in
Review of Progress
in Quantitative Nondestructive Evaluation, Vol 5, D.O. Thompson and D.E. Chimenti, Ed.
, Plenum Press,
1986, p 911
9.
B.A. Auld, General Electromechanical Reciprocity Relations Applied to the Calculation of Elastic Wave
Scattering Coefficients, Wave Motion, Vol 1, 1979, p 3
10.
R.B. Thompson and T.A. Gray, A Model Relating Ultrasonic Scattering Measurements Through Liquid-
Solid Interfaces to Unbounded Medium Scattering Amplitudes, J. Acoust. Soc. Am., Vol 74, 1983, p 1279
11.
R.B. Thompson and T.A. Gray, Analytical Diffraction Corrections to Ultrasonic Scattering Measurements,
in Review of Progress in Quantitative Nondestructive Evaluation,
Vol 2, D.O. Thompson and D.E.
Chimenti, Ed., Plenum Press, 1983, p 567
12.
R.B. Thompson and E.F. Lopes, The Effects of Focusing and Refraction on Gaussian Ultrasonic Beams,
J.
Nondestr. Eval., Vol 4, 1984, p 107
13.
R.B. Thompson, T.A. Gray, J.H. Rose, V.G. Kogan, and E.F. Lopes, The Radiation of Elliptical and
Bicylindrically Focused Piston Transducers, J. Acoust. Soc. Am., Vol 82, 1987, p 1818
14.
B.P. Newberry and R.B. Thompson, A Paraxial Theory f
or the Propagation of Ultrasonic Beams in

Anisotropic Solids, J. Acoust. Soc. Am., to be published
15.
B.P. Newberry, R.B. Thompson and E. F. Lopes, Development and Comparison of Beam Models for Two-
Media Ultrasonic Inspection, in Review of Progress in Quantitative Nondestructive Evaluation,
Vol 6, D.O.
Thompson and D.E. Chimenti, Ed., Plenum Press, 1987, p 639
16.
C.F. Ying and R. Truell, Scattering of a Plane Longitudinal Wave by a Spherical Obstacle in an
Isotropically Elastic Solid, J. Appl. Phys., Vol 27, 1956, p 1086
17.
J.L. Opsal and W.M. Visscher, Theory of Elastic Wave Scattering: Applications of the Method of Optimal
Truncation, J. Appl. Phys., Vol 58, 1985, p 1102
18.
J.-S. Chen and L.W. Schmerr, Jr., The Scattering Response of Voids--A Secon
d Order Asymptotic Theory,
in Review of Progress in Quantitative NDE,
Vol 7, D.O. Thompson and D.E. Chimenti, Ed., Plenum Press,
1988, p 139
19.
L. Adler and J.D. Achenbach, Elastic Wave Diffraction by Elliptical Cracks: Theory and Experiment,
J.
Nondestr. Eval., Vol 1, 1980, p 87
20.
B.D. Cook and W.J. Arnoult III, Gaussian-
Laguerre/Hermite Formulation for the Nearfield of an Ultrasonic
Transducer, J. Acoust. Soc. Am., Vol 59, 1976, p 9
21.
J.D. Achenbach, A.K. Gautesen, and H. McMaken, Ray Methods for Waves in Elastic Solids,
Pittman
Publishing, 1982
22.
S.O. Rice, Mathematical Analysis of Random Noise, Bell Syst. Tech. J.,
Vol 23, 1944, p 282; Vol 24, 1945,
p 96
Models for Predicting NDE Reliability
J.N. Gray, T.A. Gray, N. Nakagawa, and R.B. Thompson, Center for NDE, Iowa State University
Eddy Current Inspection Model
The eddy current NDE method has a long history of use (Ref 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, and 34). Because
of its conceptually straightforward design principle, the method allows measurements to be made in a noncontacting,
single-sided inspection geometry. Eddy current is therefore a cost-effective and truly nondestructive method of
inspection. However, as a fully quantitative method, eddy current inspection has not achieved the level of sophistication
found in other methods, such as ultrasonics and x-ray radiography. The reason for the delay in its development is
associated with the fundamental nature of the measurement. In essence, the measurement response is a complex function
of the probe fields and their interaction with the flaw, and it is difficult to isolate these two contributions. Therefore, one
cannot develop simple models in which various effects can be described by separate factors, as in the case of ultrasonics.
A significant problem has also been obtaining material property data (such as permeability and conductivity) for complex
engineering materials. Welds are especially difficult.
From a modeling perspective, it is necessary to obtain electromagnetic field solutions for a given probe/flaw system by
solving Maxwell's equations. When written in the form suitable to eddy current problems, the equations show that the
basic dynamics are of a dissipative, nonscattering nature. One well-known consequence is that only near-surface flaws,
confined within a region of a finite skin depth, are detectable. Putting this obvious limitation aside, there is a subtler
problem posed by the basic principle. Namely, electromagnetic fields spread over a wide region outside the specimen,
permitting no simple way of focusing the probe sensitivity to flaw regions. (In the other inspection methods, the beam
focusing, for example, can be used for this purpose). The impedance signal, being an integrated quantity, contains not
only flaw information but also redundant environment information (such as probe lift-off), which is uninteresting in terms
of flaw detection and characterization and may contribute significant noise. Extracting flaw information from impedance
signals therefore becomes highly dependent on component geometry and is a computationally intensive task.
Many efforts have been devoted to overcoming this difficulty, and the results have been promising (Ref 25, 26, 27, 28,
29, 30, 31, and 32). Rapid progress has occurred recently in computational methods with regard to both hardware and
software. It appears that the new-generation desktop workstations are sufficiently capable of handling the computational
requirements of eddy current data analyses. One may find an even better situation when using eddy current models to
