ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control

Подождите немного. Документ загружается.

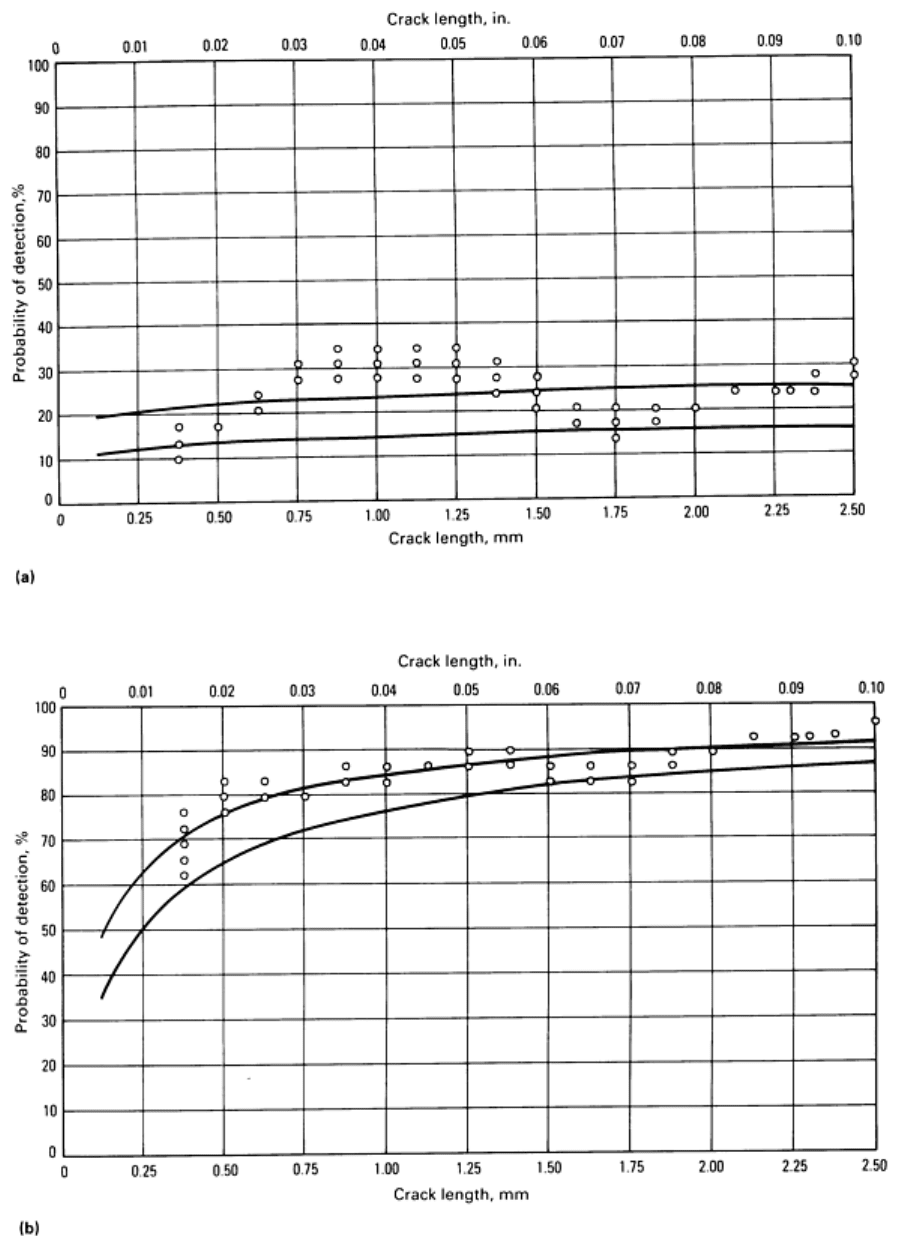
Fig. 10 POD plotted (a) at a threshold of 3.0 mV and (b) at a threshold of 0.5 mV

Integrated Blade Inspection System. The quantitative assessment of process performance capabilities and process

characterization is absolutely necessary in implementing automated NDE systems. At a gas turbine overhaul facility, for

example, quantitative assessment methods were applied to the implementation of an integrated blade inspection system

with an automated fluorescent penetrant inspection module (Fig. 11). The processed blades are introduced into a robotic

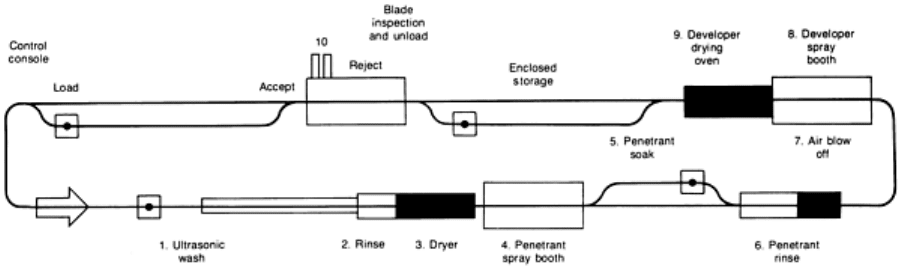
handling system that manipulates the blade in a high-gain optical-laser scan readout system to produce a digitized image

of the fluorescent penetrant indications. A computerized data processing and image analysis system provides the readout

and decision processing to accept or reject the blades.

Fig. 11 Flow diagram of an automated fluorescent penetrant inspection system

The optical performance capabilities of the readout system enable the detection of very small indications of varying

brightness level. The performance of the system is therefore limited by the fluorescent process capabilities and by the

pattern recognition capabilities of the system. Signal/noise distributions must be addressed by the decision discrimination

process, as shown in Fig. 12. Actual signal/noise distributions measured for the system are shown in Fig. 13. If the

discrimination threshold is set too low, a high false call rate will reduce the effectiveness of the automated process. A

balance of discrimination at an acceptable false call rate is used to achieve the figure of merit of performance level (Fig.

14) for the system. Signal/noise distribution data can be used to manage the overall process at any desired

discrimination/false call level. The process can be modeled to establish performance at varying discrimination levels, as

shown in Fig. 15. Quantification and characterization of process parameters are essential for the design, implementation,

and management of automated NDE processes.

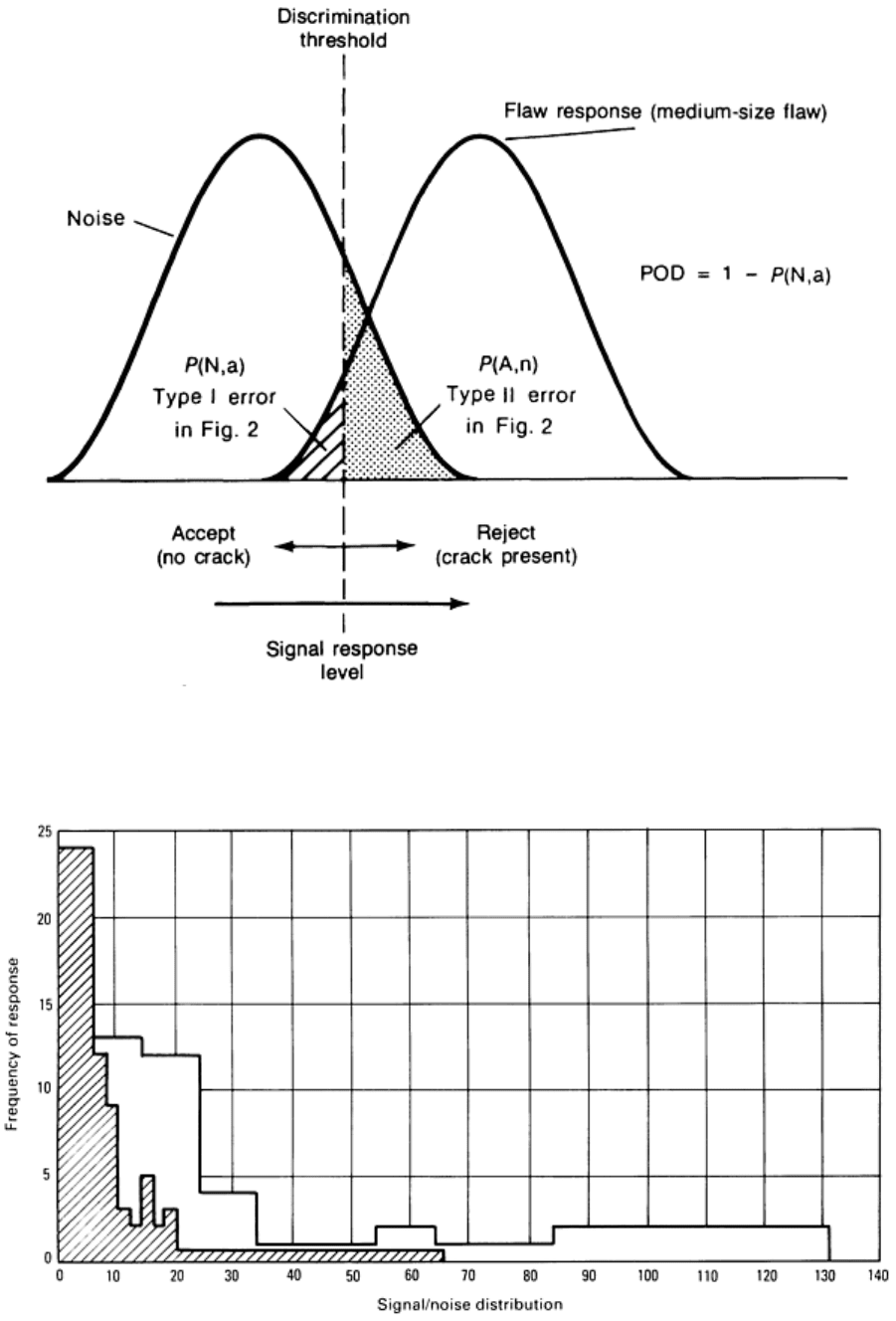
Fig. 12 Probability distribution of a noise signal and flaw indication

Fig. 13 A sample of the signal/noise distribution for an integrated blade inspection system

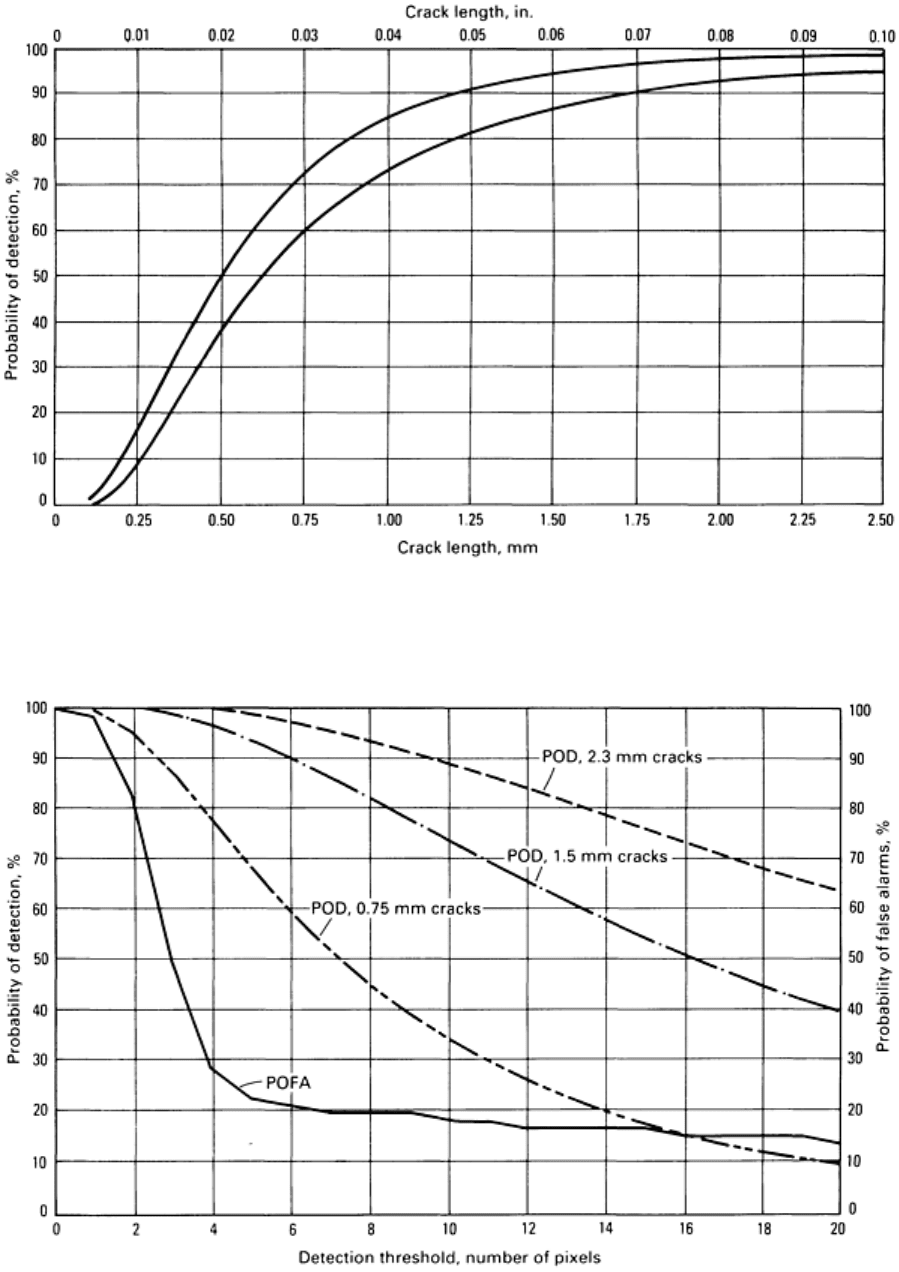
Fig. 14 POD curve for an automated fluorescent penetrant inspection system

Fig. 15 Performance curves for various discrimination levels

Retirement-For-Cause (RFC) Inspection Equipment. As described previously, the concept of removing critical

rotating components from gas turbine engines because of the initiation of an actual flaw rather than on the basis of an

arbitrarily selected time period has already saved the Air Force significant sums of money. One of the key technologies

that has allowed the RFC concept to be accepted has been the development of an accurate, repeatable, reliable inspection

system capable of finding very small flaws in the parts. The RFC system, developed under an Air Force Manufacturing

Technology contract, has been in operation at the San Antonio Air Logistics Center at Kelly Air Force Base since late

1986. It was developed under a contract with Systems Research Laboratories, and although applied specifically to parts

for the F-100 engine (used in the F-15 and F-16 aircraft), it was designed to be sufficiently flexible to inspect parts from

any gas turbine engine. This capability was achieved through the use of a team of subcontractors on the program that

included Pratt & Whitney, General Electric, Garrett, and Allison.

Eddy current methods for surface flaw detection and ultrasonic methods for detecting embedded flaws were the two

inspection techniques selected for the RFC system. Significant advances had been made in automating eddy current

inspection through the development of the Eddy Current II system by the General Electric Company on earlier Air Force

Manufacturing Technology contracts. These stand-alone automated eddy current devices are in use at the Alameda Naval

Air Rework Facility, as previously discussed; the Oklahoma City Air Logistics Center; the General Electric

Manufacturing facility in Evandale, OH; and other commercial overhaul facilities. The technology developed and proved

in these systems provided an excellent base for the evolution of the more complex RFC system.

The RFC inspection system, which is housed in the special facility shown in Fig. 16, consists of an operator console, a

system computer, and eddy current and ultrasonic inspection stations. The operator console is used to monitor the

operational status of the system, to track inspection status at each NDE station, and to generate inspection data reports.

The system computer performs advanced data processing, system-wide communication, and sophisticated high-speed

mathematical and scientific data analyses critical to the inspection process. The NDE inspection stations perform the

automated part inspections, flaw detection, and signal-preprocessing activities. The system functions essentially

independent of any human operator input, with the exception of loading and unloading the parts to be inspected onto the

stations.

Fig. 16 Retirement-for-cause inspection facility

When the system was installed, a series of critical tests was conducted to establish its flaw size detection capability and

reliability. Tests included automatic scans of engine disks and a statistically significant number of representative fatigue-

cracked test specimens. Rivet hole inspection data showed a 90% POD with a 95% CL at the 100 m (4 mil) crack depth

range. Bolt hole and flat surface data indicated reliable detection in the desired 125 to 250 m (5 to 10 mil) depth range.

A strong correlation between apparent versus actual flaw depth data was seen in all test data. The ultrasonic inspection

data were similarly encouraging. Examples of POD at 95% CL generated for various geometrical configurations are

shown in Fig. 17. A similar facility is to be installed at the Air Force engine maintenance depot at the Oklahoma City Air

Logistics Center at Tinker Air Force Base.

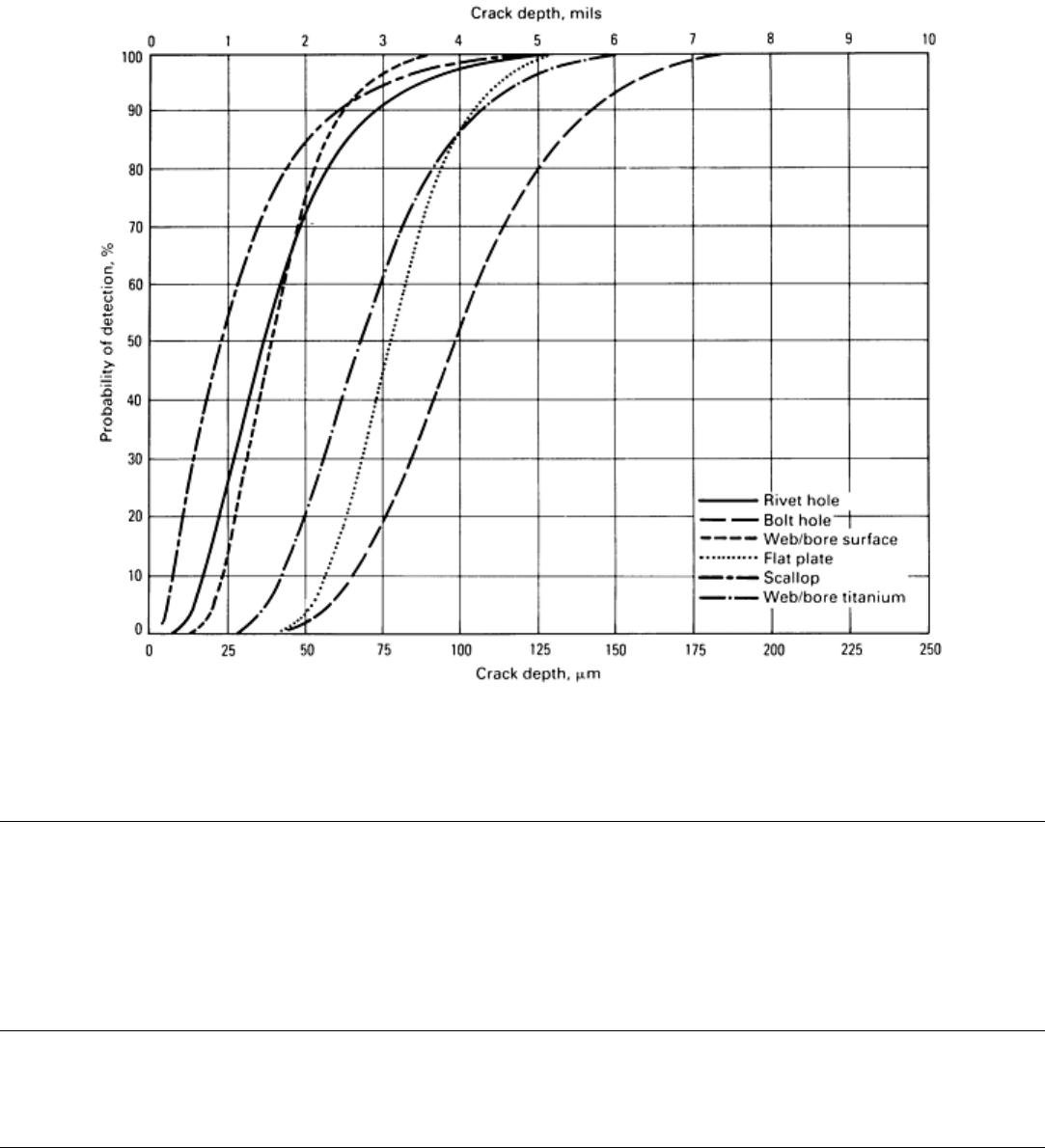
Fig. 17 RFC system POD curves for various geometrical features

References cited in this section

"Engine Structural Integrity Program (ENSIP)," MIL-STD-1783 (USAF), 30 Nov 1984

"Aircraft Structural Integrity Program, Airplane Requirements," MIL-STD-1530A (USAF), 11 Dec 1975

W.D. Rummel, P.H. Todd, Jr., S.A. Frecska, and R.A. Rathke, "The Detection of Fatigue Cracks by

Nondestructive Testing Methods," CR-2369, National Aeronautics and Space Administration, Feb 1974

Applications of NDE Reliability to Systems

Ward D. Rummel, Martin Marietta Astronautics Group; Grover L. Hardy and Thomas D. Cooper, Wright Research & Development

Center, Wright-Patterson Air Force Base

References

1. "Nondestructive Testing Personnel Qualification and Certification," MIL-STD-410D, 25 June 1974

2. "Engine Structural Integrity Program (ENSIP)," MIL-STD-1783 (USAF), 30 Nov 1984

3. "Aircraft Structural Integrity Program, Airplane Requirements," MIL-STD-1530A (USAF), 11 Dec 1975

W.D. Rummel, P.H. Todd, Jr., S.A. Frecska, and R.A. Rathke, "The Detection of Fatigue Cracks by

Nondestructive Testing Methods," CR-2369, National Aeronautics and Space Administration, Feb 1974

NDE Reliability Data Analysis

Alan P. Berens, University of Dayton Research Institute

Introduction

INSPECTION SYSTEMS are inevitably driven to their extreme capability for finding small flaws. When applied at this

extreme, not all flaws of the same size will be detected. In fact, repeat inspections of the same flaw will not necessarily

produce consistent hit or miss indications, and different flaws of the same size may have different detection probabilities.

Because of this uncertainty in the inspection process, capability is characterized in terms of the probability of detection

(POD) as a function of flaw size, a. At present, the function POD(a) can be estimated only through inspection reliability

experiments on specimens containing flaws of known size. Further, statistical methods must be used to estimate the

parameters of the POD(a) function and to quantify the experimental error in the estimated capability.

The methods for analyzing NDE reliability data have undergone a considerable evolution since the middle of the 1970s.

Formerly, a constant probability of detection of all flaws of a given size was postulated, and binomial distribution

methods were used to estimate this probability and its lower confidence bound (Ref 1, 2). This nonparametric method of

analysis produced valid statistical estimates for a single flaw size, but required very large sample sizes to obtain

reasonable lower confidence bounds on the probability of detection. In the absence of large numbers of representative

specimens with equal flaw sizes, various methods were devised for analyzing data based on grouping schemes. Although

the resulting POD appeared more acceptable using these schemes, the lower confidence bounds were no longer valid.

In recent years, an approach based on the assumption of a model for the POD(a) function was devised (Ref 3, 4, 5, 6, 7).

Analyses of data from reliability experiments on nondestructive inspection (NDI) methods indicated that the POD(a)

function can be reasonably modeled by the cumulative log normal distribution function or, equivalently, the log-logistics

(log odds) function. The parameters of these functions can be estimated using maximum likelihood methods. The

statistical uncertainty in the estimate of NDI reliability has traditionally been reflected by a lower (conservative)

confidence bound on the POD(a) function. The asymptotic statistical properties of the maximum likelihood estimates can

be used to calculate this confidence bound. Details of the mathematics for these maximum likelihood calculations are

presented in this article.

References

B.G.W. Yee, F.H. Chang, J.C. Couchman, G.H. Lemon, and P.F. Packman, "Assessm

ent of NDE Reliability

Data," NASA CR-134991, National Aeronautics and Space Administration, Oct 1976

W.D. Rummel, Recommended Practice for Demonstration of Nondestructive Evaluation (NDE) Reliability

on Aircraft Production Parts, Mater. Eng., Vol 40, Aug 1982, p 922-932

W.H. Lewis, W.H. Sproat, B.D. Dodd, and J.M. Hamilton, "Reliability of Nondestructive Inspections--

Final

Report," SA-ALC/MME 76-6-38-1, San Antonio Air Logistics Center, Kelly Air Force Base, Dec 1978

A.P. Berens and P.W. Hovey, "Evaluation of NDE Reliability Characterization," AFWAL-TR-81-

4160, Vol

1, Air Force Wright-Aeronautical Laboratories, Wright-Patterson Air Force Base, Dec 1981

A.P. Berens and P.W. Hovey, Statistical Methods for Estimating Crack Detection Probabiliti

es, in

Probabilistic Fracture Mechanics and Fatigue Methods: Applications for Structural Design and

Maintenance,

STP 798, J.M. Bloom and J.C. Ekvall, Ed., American Society for Testing and Materials, 1983,

p 79-94

D.E. Allison et al., "Cost/Risk Analysis for Disk Retirement--Volume I," AFWAL-TR-83-

4089, Air Force

Wright-Aeronautical Laboratories, Wright-Patterson Air Force Base, Feb 1984

A.P. Berens and P.W. Hovey, "Flaw Detection Reliability Criteria, Volume I--

Methods and Results,"

AFWAL-TR-84-4022, Air Force Wright-Aeronautical Laboratories, Wright-

Patterson Air Force Base, April

1984

NDE Reliability Data Analysis

Alan P. Berens, University of Dayton Research Institute

Statistical Nature of the NDE Process

In the application of an NDE method there are many factors that can influence whether or not the inspection will result in

the correct decision as to the absence or presence of a flaw. In general, NDE comprises the application of a stimulus to a

structure and the interpretation of the response to the stimulus. Repeated inspections of a specific flaw can produce

different magnitudes of stimulus response because of minute variations in setup and calibration. This variability is

inherent in the process. Different flaws of the same size can produce different response magnitudes because of differences

in material properties, flaw geometry, and flaw orientation. The interpretation of the response can be influenced by the

capability of the interpreter (manual or automated), the mental acuity of the inspector as influenced by fatigue or

emotional outlook, and the ease of access and the environment at the inspection site. All these factors contribute to

inspection uncertainty and lead to a probabilistic characterization of inspection capability.

There are two related approaches to a probabilistic framework for analyzing inspection reliability data. Originally,

inspection results were recorded only in terms of whether or not a flaw was found. Data of this nature are called hit/miss

data, and an analysis method for this data type evolved from the original binomial characterization (Ref 3, 4, 5). It was

later observed that there is more information in the NDE signal response from which the hit/miss decision is made (Ref

6). Because the NDE signal response can be considered to be the perceived flaw size, data of this nature are called data.

A second analysis method was developed based on data (Ref 7). Although the analysis frameworks are based on data of

different natures, the hit/miss data can be obtained from data. Both methods are based on the same model for the

POD(a) function, but different results will be obtained if the two analysis methods are applied to the same data set. The

following sections present the two approaches to formulating the POD(a) function.

POD(a) From Hit/Miss Data. In typical NDE reliability studies, relatively few inspections are performed on each

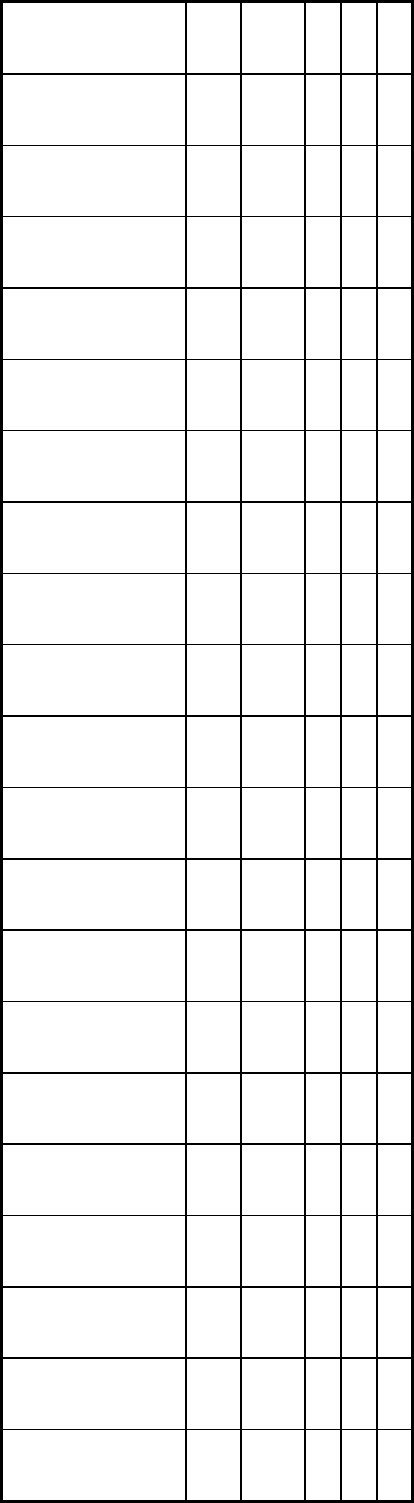
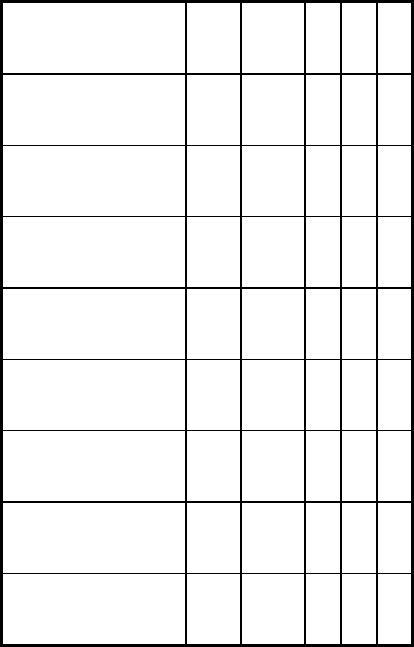
flaw in the specimen set. Table 1 presents an example of hit/miss results from fluorescent penetrant inspections by 3

inspectors on 35 cracks in flat plate specimens. Because there are only three inspections, it is impossible to obtain more

than a general impression of any change in the chances of crack detection as the cracks get larger. In a study for the Air

Force (Ref 3), inspections of cracked specimens were independently conducted by large numbers of inspectors around the

country. The data from this program provided considerable insight into the nature of the probability of crack detection.

Table 1 Example of summary data sheet of hit/miss results

The example is based on the fluorescent penetrant inspection of flat plates by three inspectors.

Crack size

Inspector

(a)

Crack identification

in. A

1 2.21

0.087

2 1.63

0.064

1 0

3 0.38

0.015

4 2.84

0.112

1 1

5 0.99

0.039

6 4.42

0.174

1 1

7 2.97

0.117

1 1

8 2.06

0.081

9 0.46

0.018

10 4.22

0.166

1 0

11 2.54

0.100

1 0

12 1.98

0.078

1 1

13 0.64

0.025

14 2.18

0.086

1 0

15 2.64

0.104

16 2.49

0.098

17 2.41

0.095

1 0

18 1.42

0.056

19 0.20

0.008

20 0.58

0.023

21 6.99

0.275

1 1

22 3.30

0.130

23 6.20

0.244

1 1

24 2.03

0.080

25 1.85

0.073

26 4.95

0.195

1 1

27 0.23

0.009

28 2.13

0.084

29 5.59

0.220

1 1

30 1.02

0.040

31 0.99

0.039

32 2.18

0.086

33 0.25

0.010

34 4.09

0.161

35 0.51

0.020

(a)

1 indicates crack was found; 0 indicates crack was not found.

Figure 1 shows the results of eddy current inspections by 60 different inspections of a set of 41 cracks around countersunk

fastener holes in a 1.5 in (5 ft) segment of a C-130 center wing box (Ref 3). Each data point represents the proportion of

times that the crack was found. This data set, which is representative of such available data sets, clearly indicates that:

• The chances of detection are correlated with crack size

• Different cracks of the same size can have significantly different crack detection probabilities

• Factors other than size are affecting the chances of detection

Data of this nature also provide the analysis framework for characterizing NDE reliability for the general hit/miss data set.