Аскирка В.Ф. Механика, молекулярная физика, термодинамика

Подождите немного. Документ загружается.

121

RTm

+=+=

. (4)

Молярная масса смеси может быть определена из соотноше-

ния

, так как количество вещества смеси есть сум-

ма количеств вещества отдельных ее составляющих, следова-

тельно,

2211

MmMm

. (5)

Подставляя числовые значения в (4) и (5), получаем:

1093,24

30031,8

100,2

100,4

×=

p Па 5,2

МПа,

100,3

100,22100,44

0,20,4

×=

×+×

кг/моль.

Ответ: 5,2

p МПа,

100,3

×=M кг/моль.

Пример 2. В запаянной с одного конца стеклянной трубке

длиной 90 см находится столбик ртути высотой 30 см, который

доходит до верхнего края. Трубку осторожно переворачивают от-

крытым концом вниз, причем часть ртути выливается. Какова вы-

сота столбика ртути, который останется в трубке, если атмосфер-

ное давление 100 кПа?

Дано:

l см 90,0

м,

h см 30,0

м,

100

=p кПа

100,1 ×= Па.

Найти:

Решение. Когда трубка расположена открытым концом вверх

(рис. 2.9), то объем части трубки, занимаемой воздухом

V , и дав-

ление в трубке

p будут равны:

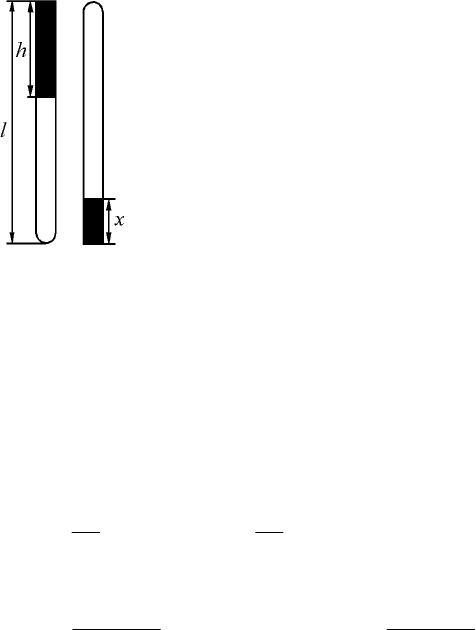
122

(

)

ShlV -=

где S – площадь поперечного сечения

трубки,

ghpp r+=

где

10613 ×=r , кг/м

– плотность ртути, gh

–

гидростатическое давление столбика ртути,

оказываемое на газ.

Когда трубка расположена открытым кон-

цом вниз (рис. 2.9), то объем, занимаемый воз-

духом

V , и давление в трубке

p будут равны:

(

)

SxlV -=

, gxpp r-=

где х – высота столбика ртути.

По закону Бойля-Мариотта [9.6]:

2211

VpVp = ,

или

(

)

(

)

(

)

(

)

gxpSxlghpShl r--=r+-

откуда

+-+

hlhxl

x .

Подставляя числовые данные, имеем:

1013600

101

3,09,03,09,0

1013600

101

+-+

- xx ,

Решая квадратное уравнение относительно

, получим:

04,064,1

=+- xx ,

34,1

=x м, 30,0

=x м.

Отбрасывая не имеющий физического смысла корень

x , при

котором lx

, окончательно имеем 30,0

x м.

Ответ: 30,0

x м.

Пример 3. В теплоизолированном цилиндре под поршнем на-

ходится 20 г гелия. При медленном перемещении поршня газ пе-

Рис. 2.9

123

реводится из состояния, которому отвечают объем, равный 32 л, и

давление 400 кПа в состояние, при котором объем 9,0 л и давление

1,55 МПа. Какова будет наибольшая температура газа при этом

процессе, если давление газа является линейной функцией объема?

Дано:

m г 020,0

кг,

=V л

1023

×= , м

400

=p кПа

100,4 ×= Па,

0,9

=V л

100,9

×= м

55,1

=p МПа

1055,1 ×= Па.

Найти:

max

T .

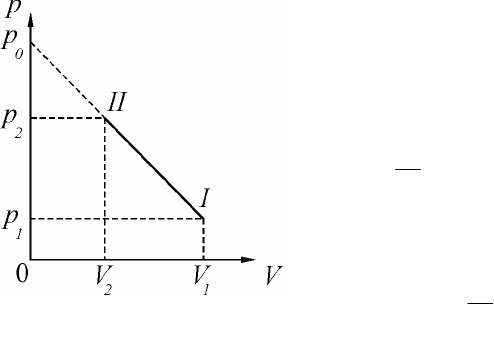
Решение. В соответствии с условием задачи зависимость дав-

ления от объема представляет собой линейную зависимость:

aVpp -=

, (1)

где

p – начальное давление, которое изображается отрезком на

оси давлений, отсекаемым продолжением I-II, и

– постоянная,

имеющая размерность Н/м

. График зависимости представлен на

рисунке 2.10.

Так как процесс расширения

проходит медленно, то каждая

точка прямой I-II соответствует

определенному состоянию газа,

параметры которого удовлетво-

ряют уравнению Менделеева-

Клапейрона:

pV = . (2)

Выражение (2) можно пере-

писать так:

()

VaVp =-

Рис. 2.10

124

Отсюда получаем зависимость температуры газа от его

объема:

(

)

aVVp

T -= .

Для нахождения объема газа при максимальном значении

температуры приравняем к нулю производную

()

=-=aVp

отсюда apV 2

0max

= .

Из соотношения (2) находим давление

max

p при максималь-

ной температуре:

0max

pp = .

Максимальную температуру определяем, воспользовавшись

уравнением состояния газа (2):

maxmaxmax

T = .

Значение

найдем из графика:

Для нахождения

p воспользуемся зависимостью давления

от объема, записав для двух состояний:

101

aVpp -= ,

202

aVpp -= .

Откуда находим:

2112

VpVp

Подставляя данные, приведенные в условии задачи, по-

лучаем:

100,5

100,91032

1040,01055,1

×=

×-×

Н/м

;

125

3636

1020

100,91032

100,91040,010321055,1

×=

×-×

×××-×××

Па;

0max

10102 ×== pp Па;

0max

100,22

×== apV м

;

481100,2100,1

31,8020,0

100,4

max

»××××

T К.

Ответ: 481

max

=T К.

Пример 4. Определить среднюю арифметическую скорость

молекул идеального газа, плотность которого при давлении 35 кПа

составляет 0,30 кг/м

Дано:

p кПа

105,3 ×= Па,

30,0

кг/м

Найти: u .

Решение. Согласно основному уравнению молекулярно-

кинетической теории идеальных газов [10.1]:

(

)

кв

nmp u= , (1)

где

– концентрация молекул,

m – масса одной молекулы,

кв

u – средняя квадратичная скорость молекул.

Учитывая выражения для определения средней арифметиче-

ской [10.5]

(

)

8 mkT p=u и средней квадратичной [10.3]

3 mkT

кв

=u скоростей движения молекул, получим соотно-

шение:

кв

. (2)

Так как плотность газа определяется выражением:

nmVNmVm ===r ,

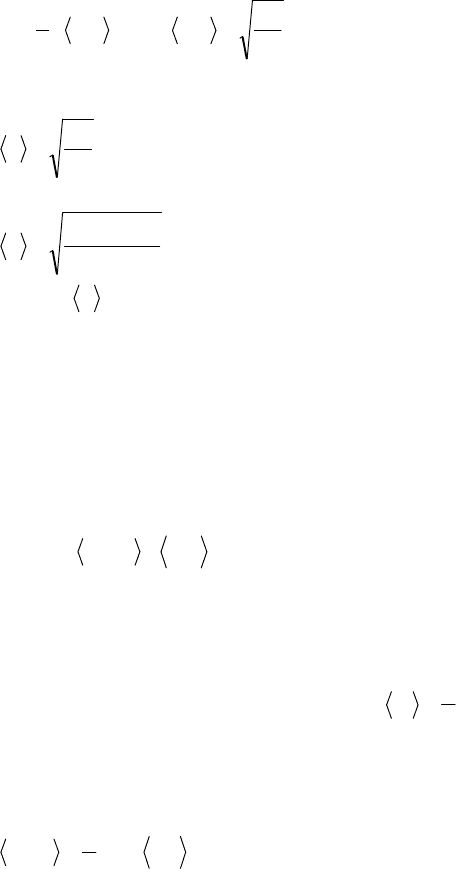
126

где

– масса газа, V – его объем, N – число всех молекул газа,

то выражение (1) можно записать в виде:

кв

p ur= или

кв

. (3)

Подставляя (3) в соотношение (2), находим искомую сред-

нюю арифметическую скорость:

Подставляя числовые значения величин, получим:

545

30,014,3

105,38

××

=u м/с.

Ответ: 545=u м/с.

Пример 5. Чему равны средние кинетические энергии посту-

пательного и вращательного движений всех молекул, содержа-

щихся в 2,0 кг водорода при температуре 400 К?

Дано:

0,2

m кг,

400

T К,

1002

×= ,M кг/моль.

Найти:

пост

E ,

вр

E .

Решение. Считаем водород идеальным газом. Молекула во-

дорода двухатомная, связь между атомами считаем жесткой, тогда

число степеней свободы молекулы водорода равно 5. В среднем на

одну степень свободы приходится энергия kT

=e , где k –

постоянная Больцмана;

– термодинамическая температура. По-

ступательному движению приписывается три

(

)

3=i , а вращатель-

ному две

(

)

2=i степени свободы. Тогда энергия одной молекулы:

пост

=e , kT

вр

=e .

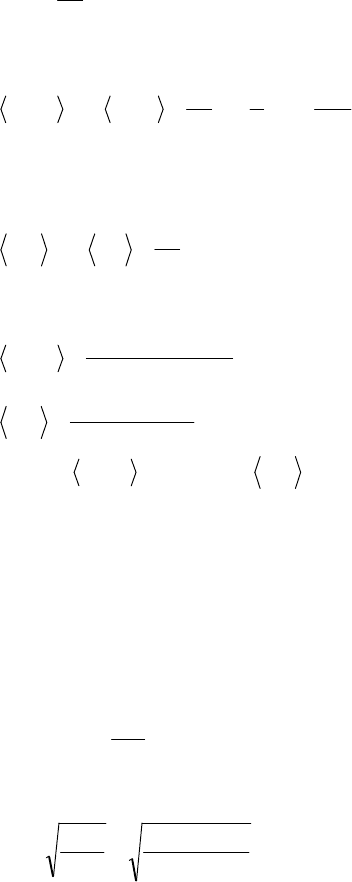
127

Число молекул, содержащихся в некоторой массе газа [9.1],

NN =n= , где

– число молей;

N – постоянная Авогад-

ро. Тогда средняя кинетическая энергия поступательного движе-

ния молекул водорода будет равна:

kTN

Aпостпост

==e= , (1)

где

kNR = – универсальная газовая постоянная.

Средняя кинетическая энергия вращательного движения мо-

лекул водорода определяется аналогично:

врвр

=e= . (2)

Подставляя числовые значения в выражения (1) и (2),

получим:

100,5

100,22

40031,80,23

×»

××

×××

пост

Дж 0,5

МДж,

103,3

102

40031,80,2

×»

××

вр

E Дж 3,3

МДж.

Ответ: 0,5=

пост

E МДж, 3,3=

вр

E МДж.

Пример 6. Какая часть молекул водорода, находящегося при

температуре 481 К, обладает скоростями, отличающимися от наи-

вероятнейшей скорости не более чем на 5,0 м/с?

Дано:

481

T К,

0,5

м/с,

100,2

×=M кг/моль.

Найти:

=h .

Решение. Определим значение наивероятнейшей скорости

молекул водорода при данной температуре:

1002

48131822

×»

××

==u

м/с. (1)

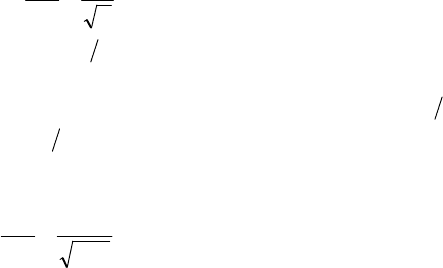
128

Поскольку интервал скоростей от uD-u

до uD+u

со-

ставляет

2 и достаточно мал по сравнению со значением най-

денной наивероятнейшей скорости, то распределение Максвелла

по относительным скоростям [11.3] можно записать в конечных

приращениях:

()

zez

. (2)

Так как

z uu= , а малый интервал скоростей 2

рассмат-

ривается относительно наивероятнейшей скорости, то в условиях

данной задачи 2000=u=u

м/с, следовательно, 1=uu=

z . При

этом 0050,02 =uuD=D

z .

Подставляя числовые значения величин в выражение (2), по-

лучим искомую часть молекул:

46,00050,01

14,3

»×=

Ответ: 46,0

Пример 7. В высоком вертикальном сосуде находится газ, со-

стоящий из двух сортов молекул с массами

m и

m (

mm > ).

Концентрации этих молекул у дна сосуда равны соответственно

n (

nn > ). Учитывая, что сосуд находится в однородном поле

тяжести (

const

) и по всей его высоте поддерживается постоян-

ная температура

, найти высоту, на которой концентрации обоих

сортов молекул будут одинаковыми.

Дано:

m ,

n ,

Найти: h .

Решение. Согласно распределению Больцмана, концентрация

молекул газа первого сорта в однородном поле тяжести при тем-

129

пературе

на некоторой высоте определяется выражением [11.4]:

(

)

kTghm

enn

, (1)

где h – высота, соответствующая концентрации

относительно

уровня, где концентрация молекул составляет

n .

Для молекул второго сорта распределение Больцмана будет

иметь вид:

(

)

kTghm

enn

. (2)

Так как на некоторой высоте концентрации молекул обоих

сортов одинаковые (

), то, приравняв правые части выраже-

ний (1) и (2), получим:

(

)

(

)

kTghmkTghm

enen

= . (3)

После преобразования выражение (3) запишется в виде:

()()

kTghmm

. (4)

После логарифмирования выражение (4) примет вид:

(

)

ghmm

Выражая искомую высоту h , окончательно получим:

()

gmm

Ответ:

()

gmm

Пример 8. Определить среднюю длину свободного пробега

молекул и число соударений за 1,0 секунду, происходящих между

всеми молекулами кислорода, находящегося в сосуде емкостью

2,0 л при температуре 27 °С и давлении 100 кПа.

Дано:

0,2

V л

100,2

×= м

1032

×=M кг/моль,

300

T К,

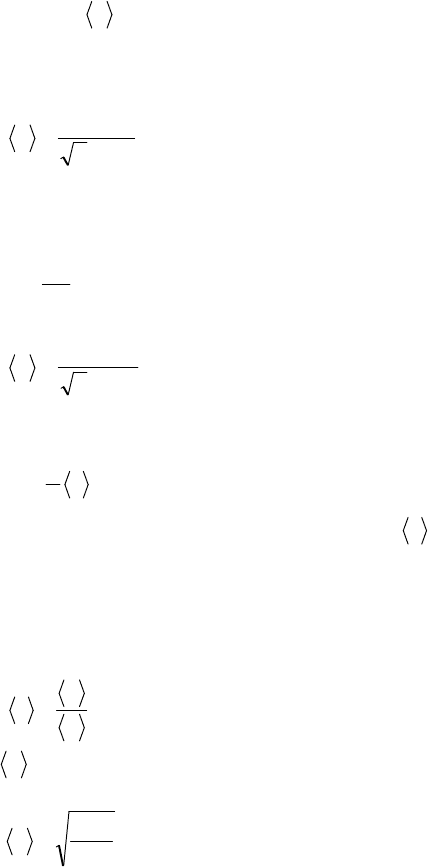
130

100

p кПа

100,1 ×= Па,

109,2

×=d м.

Найти: l ,

Решение. Средняя длина свободного пробега молекул кисло-

рода вычисляется из соотношения [12.1]:

, (1)

где d – эффективный диаметр молекулы кислорода;

– число

молекул в единице объема (концентрация), которое можно опре-

делить из уравнения [10.1] nkTp

, откуда:

n = . (2)

Подставляя (2) в соотношение (1), имеем:

=l . (3)

Число соударений

, происходящих между всеми молекула-

ми за 1,0 секунду, равно:

NzZ

= , (4)

где N – число молекул кислорода в сосуде, z – среднее число

соударений одной молекулы за 1 с. Число всех молекул в сосуде

равно:

nVN

. (5)

Среднее число соударений молекулы за 1,0 с определяется как:

=z , (6)

где u – средняя арифметическая скорость молекулы, определяе-

мая из соотношения [10.5]:

. (7)