Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

88 Chapter 2

The only nontrivial solutions to the preceding occur when C2 = 0, C1 is arbitrary, and μ

satisﬁes the following eigenvalue equation:

> sin(mu*b)=0;

sin(μb) = 0 (2.13)

Thus, μ takes on the values

> mu[n]:=n*Pi/b;

nπ

(2.14)

for n = 1, 2, 3, ....

Allowed eigenvalues are λ

= μ

> lambda[n]:=(n*Pi/b)ˆ2;

(2.15)

Nonnormalized eigenfunctions are

> phi[n](x):=sin(mu[n]*x);

(x) := sin



nπx



(2.16)

Normalization

Evaluating the norm from the inner product of the eigenfunctions with respect to the weight

function w(x) = 1 over the interval yields

> w(x):=1:unprotect(norm):norm:=sqrt(Int(phi[n](x)ˆ2*w(x),x=0..b));norm:=expand

(value(%)):

norm :=









sin



nπx



dx (2.17)

Substitution of the eigenvalue equation simpliﬁes the norm

> norm:=radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},norm));

norm :=

√

b (2.18)

Orthonormal eigenfunctions

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 89

> phi[n](x):=phi[n](x)/norm;phi[m](x):=subs(n=m,phi[n](x)):

(x) :=

sin



nπx



√

(2.19)

Statement of orthonormality

> Int(phi[n](x)*phi[m](x)*w(x),x=0..b)=delta(n,m);



2 sin



nπx



sin



mπx



dx = δ(n, m) (2.20)

Generalized Fourier series expansion

> f(x):=Sum(F(n)*phi[n](x),n=1..inﬁnity);f(x):=‘f(x)’:

f(x) :=

∞



n=1

F(n) sin



nπx



√

(2.21)

Fourier coefﬁcients

> F(n):=Int(f(x)*phi[n](x)*w(x),x=0..b);F(n):=‘F(n)’:

F(n) :=



f(x) sin



nπx



√

dx (2.22)

This is the generalized series expansion of f(x) in terms of the “complete” set of eigenfunctions

for the particular Sturm-Liouville operator and given boundary conditions over the interval.

DEMONSTRATION: Develop the generalized series expansion for f(x) = x over the interval

I ={x |0 <x<1} in terms of the preceding eigenfunctions. We assign the system values

> a:=0;b:=1;f(x):=x;

a := 0

b := 1

f(x) := x (2.23)

SOLUTION: We evaluate the Fourier coefﬁcients

> F(n):=eval(Int(f(x)*phi[n](x)*w(x),x=a..b));F(n):=value(%):

F(n) :=



x sin(nπx)

√

2dx (2.24)

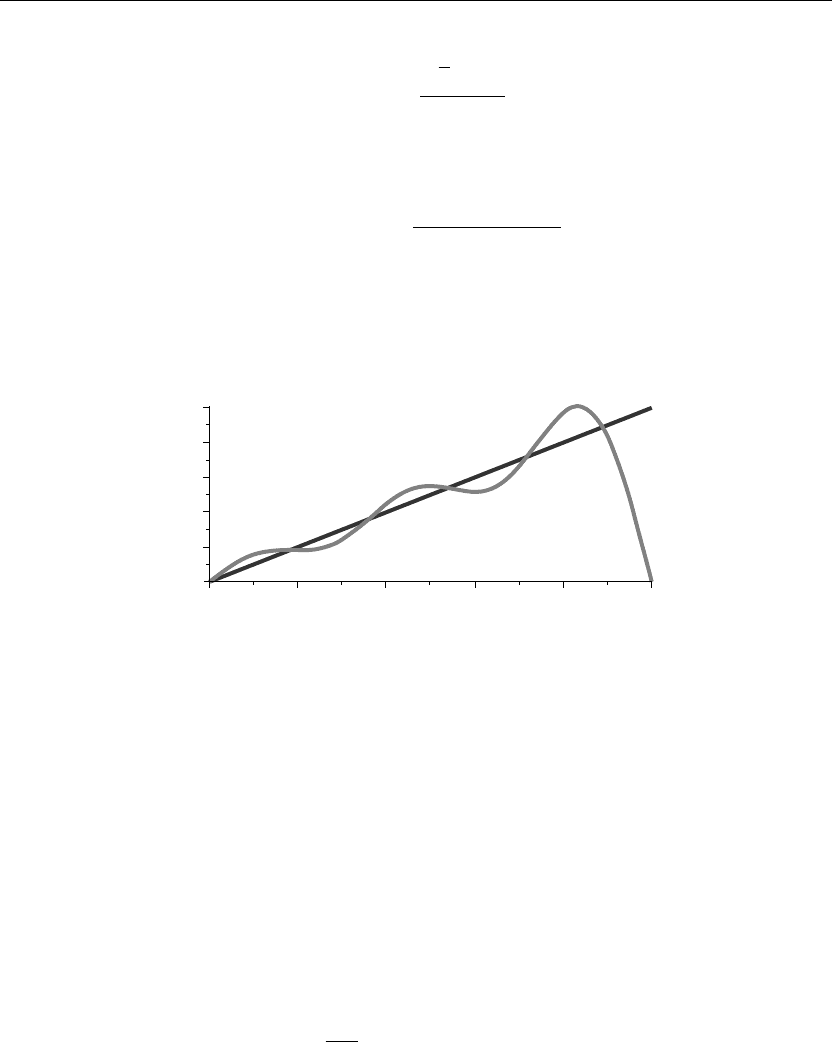
90 Chapter 2

> F(n):=subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},F(n));

F(n) := −

√

2(−1)

nπ

(2.25)

> Series:=eval(Sum(F(n)*phi[n](x),n=1..inﬁnity));

Series :=

∞



n=1



−

2(−1)

sin(nπx)

nπ



(2.26)

First ﬁve terms of expansion

> Series:=sum(F(n)*phi[n](x),n=1..5):

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Figure 2.4

The curves of Figure 2.4 depict the function f(x) and its Fourier series approximation in terms

of the orthonormal eigenfunctions for the particular operator and boundary conditions given

earlier. Note that f(x) satisﬁes the given boundary conditions at the left but fails to do so at the

right end point. The convergence is pointwise.

EXAMPLE 2.5.2: Consider the Euler operator with Dirichlet and Neumann conditions. We

seek the eigenvalues and corresponding orthonormal eigenfunctions for the Euler differential

equation [Sturm-Liouville type for p(x) = 1, q(x) = 0, w(x) = 1] over the interval

I ={x |0 <x<b}. The boundary conditions are type 1 at the left and type 2 at the right.

Euler differential equation

y(x) +λy(x) = 0

Boundary conditions

y(0) = 0 and y

(b) = 0

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 91

SOLUTION: We consider two possibilities for values of λ. We ﬁrst consider λ = 0. For this

case, the system basis vectors are

> restart:y1(x):=1;y2(x):=x;

y1(x) := 1

y2(x) := x (2.27)

General solution

> y(x):=C1*y1(x)+C2*y2(x);

y(x) := C1 +C2x (2.28)

Substituting the boundary conditions yields

> eval(subs(x=0,y(x)))=0;

C1 = 0 (2.29)

> eval(subs(x=b,diff(y(x),x)))=0;

C2 = 0 (2.30)

The only solution to the preceding is the trivial solution. We next consider λ>0. We set

λ = μ

and, for this case, the system basis vectors are

> y1(x):=sin(mu*x);y2(x):=cos(mu*x);

y1(x) := sin(μx)

y2(x) := cos(μx) (2.31)

General solution

> y(x):=C1*y1(x)+C2*y2(x);

y(x) := C1 sin(μx) +C2 cos(μx) (2.32)

Substituting the boundary conditions yields

> eval(subs(x=0,y(x)))=0;

C2 = 0 (2.33)

> eval(subs(x=b,diff(y(x),x)))=0;

C1 cos(μb)μ −C2 sin(μb)μ = 0 (2.34)

92 Chapter 2

The only nontrivial solutions occur when C2 = 0, C1 is arbitrary, and μ satisﬁes the following

eigenvalue equation:

> cos(mu*b)=0;

cos(μb) = 0 (2.35)

Thus, μ takes on values

> mu[n]:=(2*n−1)*Pi/(2*b);

(2 n −1)π

(2.36)

for n = 1, 2, 3,....

Allowed eigenvalues are λ

= μ

> lambda[n]:=mu[n]ˆ2;

(2 n −1)

(2.37)

Nonnormalized eigenfunctions are

> phi[n](x):=sin(mu[n]*x);

(x) := sin



(2n −1)πx



(2.38)

Normalization

Evaluating the norm from the inner product of the eigenfunctions with respect to the weight

function w(x) = 1 over the interval yields

> w(x):=1:unprotect(norm):norm:=sqrt(Int(phi[n](x)ˆ2*w(x),x=0..b));norm:=expand

(value(%)):

norm :=









sin



(2 n −1)πx



dx (2.39)

Substitution of the eigenvalue equation simpliﬁes the norm

> norm:=radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},norm));

norm :=

√

b (2.40)

Orthonormal eigenfunctions

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 93

> phi[n](x):=phi[n](x)/norm;phi[m](x):=subs(n=m,phi[n](x)):

(x) :=

sin



(2n−1)πx



√

(2.41)

Statement of orthonormality

> Int(phi[n](x)*phi[m](x)*w(x),x=0..b)=delta(n,m);



2 sin



(2 n−1)πx



sin



(2 m−1)πx



dx = δ(n, m) (2.42)

Generalized Fourier series expansion

> f(x):=Sum(F(n)*phi[n](x),n=1..inﬁnity);f(x):=‘f(x)’:

f(x) :=

∞



n=1

F(n) sin



(2n−1)πx



√

(2.43)

Fourier coefﬁcients

> F(n):=Int(f(x)*phi[n](x)*w(x),x=0..b);F(n):=‘F(n)’:

F(n) :=



f(x) sin



(2n−1)πx



√

dx (2.44)

This is the generalized series expansion of f(x) in terms of the “complete” set of eigenfunctions

for the particular Sturm-Liouville operator and boundary conditions over the interval.

DEMONSTRATION: Develop the generalized series expansion for f(x) = x over the interval

I ={x |0 <x<1} in terms of the preceding eigenfunctions. We assign the system values

> a:=0;b:=1;f(x):=x;

a := 0

b := 1

f(x) := x (2.45)

SOLUTION: We evaluate the Fourier coefﬁcients

> F(n):=eval(Int(f(x)*phi[n](x)*w(x),x=a..b));F(n):=value(%):

F(n) :=



x sin



(2n −1)πx



√

2dx (2.46)

94 Chapter 2

> F(n):=subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn,sin((2*n+1)/2*Pi)=(−1)ˆn,

cos((2*n+1)/2*Pi)=0},F(n));

F(n) := −

√

2(−1)

(4n

−4n +1)

(2.47)

> Series:=eval(Sum(F(n)*phi[n](x),n=1..inﬁnity));

Series :=

∞



n=1

⎛

⎝

−

8 (−1)

sin



(2 n −1)πx



(4 n

−4 n +1)

⎞

⎠

(2.48)

First ﬁve terms of expansion

> Series:=eval(sum(F(n)*phi[n](x),n=1..5)):

> plot({Series,f(x)},x=0..b,thickness=10);

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Figure 2.5

The two curves of Figure 2.5 depict the function f(x) and its Fourier series approximation in

terms of the orthonormal eigenfunctions for the particular operator and boundary conditions

given earlier. Note that f(x) satisﬁes the given boundary conditions at the left but fails to do so

at the right end point. The convergence is pointwise.

EXAMPLE 2.5.3: Consider the Euler operator with Neumann conditions. We seek the

eigenvalues and corresponding orthonormal eigenfunctions for the Euler differential equation

[Sturm-Liouville type for p(x) = 1, q(x) = 0, w(x) = 1] over the interval I ={x |0 <x<b}.

The boundary conditions are type 2 at the left and type 2 at the right end points.

Euler differential equation

y(x) +λy(x) = 0

Boundary conditions

(0) = 0 and y

(b) = 0

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 95

SOLUTION: We consider two possibilities for values of λ. We ﬁrst consider λ = 0. For this

case, the system basis vectors are

> restart:y1(x):=1;y2(x):=x;

y1(x) := 1

y2(x) := x (2.49)

General solution

> y(x):=C1*y1(x)+C2*y2(x);

y(x) := C1 +C2x (2.50)

Substituting into the boundary conditions yields

> eval(subs(x=0,diff(y(x),x)))=0;

C2 = 0 (2.51)

> eval(subs(x=b,diff(y(x),x)))=0;

C2 = 0 (2.52)

The only nontrivial solution to the above occurs when C2 = 0 and C1 is arbitrary. Thus, our

eigenvalue and corresponding eigenfunction for λ = 0 are

> lambda[0]:=0;

:= 0 (2.53)

> phi[0](x):=1;

(x) := 1 (2.54)

We next consider λ>0. We set λ = μ

. For this case, the system basis vectors are

> y1(x):=sin(mu*x);y2(x):=cos(mu*x);

y1(x) := sin(μx)

y2(x) := cos(μx) (2.55)

General solution

> y(x):=C1*y1(x)+C2*y2(x);

y(x) := C1 sin(μx) +C2 cos(μx) (2.56)

96 Chapter 2

Substituting into the boundary conditions yields

> eval(subs(x=0,diff(y(x),x)))=0;

C1 μ = 0 (2.57)

> eval(subs(x=b,diff(y(x),x)))=0;

C1 cos(μ b)μ −C2 sin(μ b)μ = 0 (2.58)

The only nontrivial solutions to the above occur when C1 = 0, C2 is arbitrary, and μ satisﬁes

the following eigenvalue equation:

> sin(mu*b)=0;

sin(μ b) = 0 (2.59)

Thus, μ takes on values

> mu[n]:=n*Pi/b;

nπ

(2.60)

for n = 1, 2, 3, ....

Allowed eigenvalues are λ

= μ

> lambda[n]:=mu[n]ˆ2;

(2.61)

Nonnormalized eigenfunctions are

> phi[n](x):=cos(mu[n]*x);

(x) := cos



nπx



(2.62)

Normalization

Evaluating the norm from the inner product of the eigenfunctions with respect to the weight

function w(x) = 1 over the interval, yields, for n = 0

> w(x):=1:norm0:=sqrt(Int(phi[0](x)ˆ2*w(x),x=0..b));

norm0 :=









1dx (2.63)

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 97

> norm0:=value(%);

norm0 :=

√

b (2.64)

For n = 1, 2, 3,...,weget

> norm1:=sqrt(Int(phi[n](x)ˆ2*w(x),x=0..b));norm1:=expand(value(%)):

norm1 :=









cos



nπx



dx (2.65)

Substitution of the eigenvalue equation simpliﬁes the norm

> norm1:=radsimp(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},norm1));

norm1 :=

√

b (2.66)

Orthonormal eigenfunctions

> phi[0](x):=phi[0](x)/norm0;

(x) :=

√

(2.67)

> phi[n](x):=phi[n](x)/norm1;phi[m](x):=subs(n=m,phi[n](x)):

(x) :=

cos



nπx



√

(2.68)

Statement of orthonormality

> Int(phi[n](x)*phi[m](x)*w(x),x=0..b)=delta(n,m);



2 cos



nπx



cos



mπx



dx = δ(n, m) (2.69)

Generalized Fourier series expansion

> f(x):=F(0)*phi[0](x)+Sum(F(n)*phi[n](x),n=1..inﬁnity);f(x):=‘f(x)’:

f(x) :=

F(0)

√

∞



n=1

F(n) cos



nπx



√

(2.70)