Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


98 Chapter 2
Fourier coefficients
> F(n):=Int(f(x)*phi[n](x)*w(x),x=0..b);F(n):=‘F(n)’:
F(n) :=
b
0
f(x) cos
nπx
b
√
2
√
b
dx (2.71)
> F(0):=Int(f(x)*phi[0](x)*w(x),x=0..b);
F(0) :=
b
0
f(x)
√
b
dx (2.72)
This is the generalized series expansion of f(x) in terms of the “complete” set of eigenfunctions
for the particular Sturm-Liouville operator and boundary conditions over the interval.
DEMONSTRATION: Develop the generalized series expansion for f(x) = x over the interval
I ={x |0 <x<1} in terms of the preceding eigenfunctions. We assign the system values
> a:=0;b:=1;f(x):=x;
a := 0
b := 1
f(x) := x (2.73)
SOLUTION: We evaluate the Fourier coefficients
> F(n):=eval(Int(f(x)*phi[n](x)*w(x),x=a..b));F(n):=value(%):
F(n) :=
1
0
x cos(nπx)
√
2dx (2.74)
> F(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},F(n)));
F(n) :=
√
2 (−1 +(−1)
n
)
n
2
π
2
(2.75)
> F(0):=eval(Int(f(x)*phi[0](x)*w(x),x=a..b));
F(0) :=
1
0
x dx (2.76)

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 99
> F(0):=value(%);
F(0) :=
1
2
(2.77)
> Series:=eval(F(0)*phi[0](x)+Sum(F(n)*phi[n](x),n=1..infinity));
Series :=
1
2
+
∞
n=1
2
−1 +(−1)
n
cos(nπx)
n
2
π
2
(2.78)
First five terms of expansion
> Series:=eval(F(0)*phi[0](x)+sum(F(n)*phi[n](x),n=1..5)):
> plot({Series,f(x)},x=a..b,thickness=10);
x
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Figure 2.6
The two curves of Figure 2.6 depict the function f(x) and its Fourier series approximation in
terms of the orthonormal eigenfunctions for the particular operator and boundary conditions
given earlier. Note that f(x) does not satisfy either of the boundary conditions imposed on the
eigenfunctions at the end points. The convergence is pointwise.
EXAMPLE 2.5.4: Consider the Euler operator with Dirichlet and Robin conditions. We seek
the eigenvalues and corresponding orthonormal eigenfunctions for the Euler differential
equation [Sturm-Liouville type for p(x) = 1, q(x) = 0, w(x) = 1] over the interval
I ={x |0 <x<b}. The boundary conditions are type 1 at the left and type 3 at the right end
points.
Euler differential equation
d
2
dx
2
y(x) +λy(x) = 0
Boundary conditions (h>0)
y(0) = 0 and y
x
(b) +hy(b) = 0

100 Chapter 2
SOLUTION: We consider two possibilities for values of λ. We first consider λ = 0. For this
case, the system basis vectors are
> restart:y1(x):=1;y2(x):=x;
y1(x) := 1
y2(x) := x (2.79)
General solution
> y(x):=C1*y1(x)+C2*y2(x);
y(x) := C1 +C2x (2.80)
Substituting into the boundary conditions yields
> eval(subs(x=0,y(x)))=0;
C1 = 0 (2.81)
> eval(subs(x=b,diff(y(x),x)+h*y(x)))=0;
C2 +h(C1 +C2b) = 0 (2.82)
The only solution to the preceding is the trivial solution. We next consider λ>0. We set
λ = μ
2
, and for this case, the system basis vectors are
> y1(x):=sin(mu*x);y2(x):=cos(mu*x);
y1(x) := sin(μx)
y2(x) := cos(μx) (2.83)
General solution
> y(x):=C1*y1(x)+C2*y2(x);
y(x) := C1 sin(μx) +C2 cos(μx) (2.84)
Substituting into the boundary conditions yields
> eval(subs(x=0,y(x)))=0;
C2 = 0 (2.85)
> eval(subs(x=b,diff(y(x),x)+h*y(x)))=0;
C1 cos(μb)μ −C2 sin(μb)μ +h(C1 sin(μb) +C2 cos(μb)) = 0 (2.86)

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 101
The only nontrivial solutions to the preceding are that C2 = 0, C1 is arbitrary, and μ must
satisfy the following eigenvalue equation:
> h*sin(mu*b)+mu*cos(mu*b)=0;
h sin(μ b) +μ cos(μ b) = 0 (2.87)
We indicate these roots as μ
n
for n = 1, 2, 3,....
Allowed eigenvalues are λ
n
= μ
2
n
> lambda[n]=mu[n]ˆ2;
λ
n
= μ
2
n
(2.88)
Nonnormalized eigenfunctions are
> phi[n](x):=sin(sqrt(lambda[n])*x);
φ
n
(x) := sin
λ
n
x
(2.89)
Normalization
Evaluating the norm from the inner product of the eigenfunctions with respect to the weight
function w(x) = 1 over the interval yields
> w(x):=1:unprotect(norm):norm:=sqrt(Int(phi[n](x)ˆ2*w(x),x=0..b));norm:=value(%):
norm :=
b
0
sin
λ
n
x
2
dx (2.90)
Substitution of the eigenvalue equation simplifies the norm
> norm:=radsimp(subs(sin(sqrt(lambda[n])*b)=−sqrt(lambda[n])/
h*cos(sqrt(lambda[n])*b),norm));
norm :=
1
2
√
2
cos
√
λ
n
b
2
+bh
h
h
(2.91)
Orthonormal eigenfunctions
> phi[n](x):=phi[n](x)/norm;phi[m](x):=subs(n=m,phi[n](x)):
φ
n
(x) :=
sin
√
λ
n
x
√
2h
cos
√
λ
n
b
2
+bh
h
(2.92)

102 Chapter 2
Statement of orthonormality
> Int(phi[n](x)*phi[m](x)*w(x),x=0..b)=delta(n,m);
b
0
2 sin
√
λ
n
x
h
2
sin
√
λ
m
x
cos
√
λ
n
b
2
+bh
h
cos
√
λ
m
b
2
+bh
h
dx = δ(n, m) (2.93)
Generalized Fourier series expansion
> f(x):=Sum(F(n)*phi[n](x),n=1..infinity);f(x):=‘f(x)’:
f(x) :=
∞
n=1
F(n) sin
√
λ
n
x
√
2 h
cos
√
λ
n
b
2
+bh
h
(2.94)
Fourier coefficients
> F(n):=Int(f(x)*phi[n](x)*w(x),x=0..b);F(n):=‘F(n)’:
F(n) :=
b
0
f(x) sin
√
λ
n
x
√
2 h
cos
√
λ
n
b
2
+bh
h
dx (2.95)
This is the generalized series expansion of f(x) in terms of the “complete” set of eigenfunctions
for the particular Sturm-Liouville operator and boundary conditions over the interval.
DEMONSTRATION: Develop the generalized series expansion for f(x) = x over the interval
I ={x |0 <x<1} in terms of the preceding eigenfunctions for h = 1. We assign the system
values
> a:=0;b:=1;h:=1;f(x):=x;
a := 0
b := 1
h := 1
f(x) := x (2.96)
SOLUTION: We evaluate the Fourier coefficients
> F(n):=Int(eval(f(x)*phi[n](x))*w(x),x=a..b);F(n):=value(%):
F(n) :=
1
0
x sin
√
λ
n
x
√
2
cos
√
λ
n
2
+1
dx (2.97)
Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 103
Substitution of the eigenvalue equation simplifies the preceding equation:
> F(n):=simplify(subs(sin(sqrt(lambda[n])*b)=−sqrt(lambda[n])/
h*cos(sqrt(lambda[n])*b),F(n)));
F(n) := −
2
√
2 cos
√
λ
n
cos
√
λ
n
2
+1
√
λ
n
(2.98)
> Series:=simplify(Sum(F(n)*phi[n](x),n=1..infinity));
Series :=
∞
n=1
⎛
⎝
−
4 cos
√
λ
n
sin
√
λ
n
x
cos
√
λ
n
2
+1
√
λ
n
⎞
⎠
(2.99)
Evaluation of the eigenvalues from the roots of the eigenvalue equation yields
> tan(sqrt(lambda[n])*b)=−sqrt(lambda[n])/h;
tan
λ
n
=−
λ
n
(2.100)
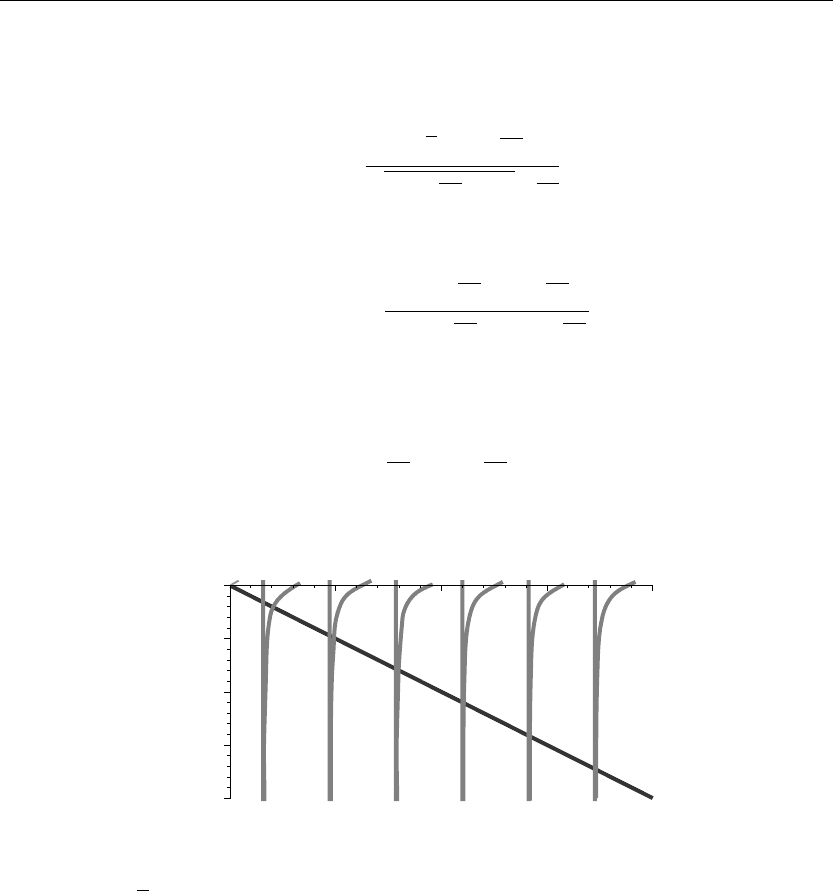
> plot({tan(v),−v/(b*h)},v=0..20,y=−20..0,thickness=10);
v
10 20
y
220
215
210
25
0
155
Figure 2.7
If we set v =
√
λb, then the eigenvalues are found from the intersection points of the curves
shown in Figure 2.7. We evaluate a few of these eigenvalues from the Maple fsolve command
for the roots of the eigenvalue equation to be given as
> lambda[1]:=(1/b*(fsolve((tan(v)+v/(h*b)),v=1..3)))ˆ2;
λ
1
:= 4.115858365 (2.101)
> lambda[2]:=(1/b*(fsolve((tan(v)+v/(h*b)),v=3..6)))ˆ2;
λ
2
:= 24.13934203 (2.102)
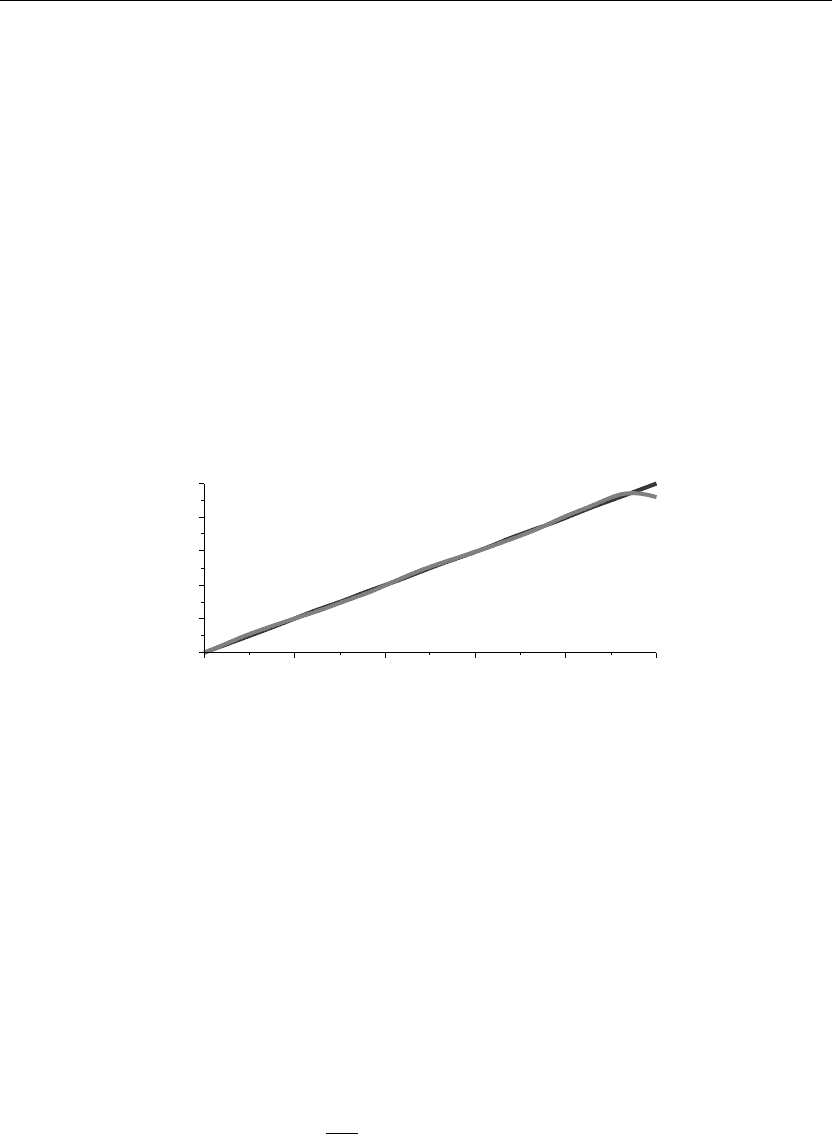
104 Chapter 2
> lambda[3]:=(1/b*(fsolve((tan(v)+v/(h*b)),v=6..9)))ˆ2;
λ
3
:= 63.65910654 (2.103)
> lambda[4]:=(1/b*(fsolve((tan(v)+v/(h*b)),v=9..13)))ˆ2;
λ
4
:= 122.8891618 (2.104)
> lambda[5]:=(1/b*(fsolve((tan(v)+v/(h*b)),v=13..16)))ˆ2;
λ
5
:= 201.8512584 (2.105)
First five terms of expansion
> Series:=eval(sum(F(n)*phi[n](x),n=1..5)):
> plot({Series,f(x)},x=a..b,thickness=10);
x
0
0.2
0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Figure 2.8
The two curves of Figure 2.8 depict the function f(x) and its Fourier series approximation in
terms of the orthonormal eigenfunctions for the particular operator and boundary conditions
given earlier. Note that f(x) satisfies the given boundary conditions at the left but fails to do so
at the right end point. The convergence is pointwise.
EXAMPLE 2.5.5: Consider the Euler operator with Neumann and Robin conditions. We seek
the eigenvalues and corresponding orthonormal eigenfunctions for the Euler differential
equation [Sturm-Liouville type for p(x) = 1, q(x) = 0, w(x) = 1] over the interval
I ={x |0 <x<b}. The boundary conditions are type 2 at the left and type 3 at the right end
points.
Euler differential equation
d
2
dx
2
y(x) +λy(x) = 0

Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 105
Boundary conditions (h>0)
y
x
(0) = 0 and y
x
(b) +hy(b) = 0
SOLUTION: We consider two possibilities for values of λ. We first consider λ = 0. For this
case, the system basis vectors are
> restart:y1(x):=1;y2(x):=x;
y1(x) := 1
y2(x) := x (2.106)
General solution
> y(x):=C1*y1(x)+C2*y2(x);
y(x) := C1 +C2x (2.107)
Substituting into the boundary conditions yields
> eval(subs(x=0,diff(y(x),x)))=0;
C2 = 0 (2.108)
> eval(subs(x=b,diff(y(x),x)+h*y(x)))=0;
C2 +h(C1 +C2b) = 0 (2.109)
The only solution to the preceding is the trivial solution. We next consider λ>0. We set
λ = μ
2
. For this case, the system basis vectors are
> y1(x):=sin(mu*x); y2(x):=cos(mu*x);
y1(x) := sin(μx)
y2(x) := cos(μx) (2.110)
General solution
> y(x):=C1*y1(x)+C2*y2(x);
y(x) := C1 sin(μx) +C2 cos(μx) (2.111)
Substituting into the boundary conditions yields
> eval(subs(x=0,diff(y(x),x)))=0;
C1 μ = 0 (2.112)

106 Chapter 2
> eval(subs(x=b,diff(y(x),x)+h*y(x)))=0;
C1 cos(μ b)μ −C2 sin(μ b)μ +h(C1 sin(μ b) +C2 cos(μ b)) = 0 (2.113)
The only nontrivial solutions to the preceding occur when C1 = 0, C2 is arbitrary, and μ
satisfies the following eigenvalue equation:
> mu*sin(mu*b)−h*cos(mu*b)=0;
μ sin(μ b) −h cos(μ b) = 0 (2.114)
We identify these roots as μ
n
for n = 1, 2, 3,....
Allowed eigenvalues are λ
n
= μ
2
n
> lambda[n]=mu[n]ˆ2;
λ
n
= μ
2
n
(2.115)
Nonnormalized eigenfunctions are
> phi[n](x):=cos(sqrt(lambda[n])*x);
φ
n
(x) := cos
λ
n
x
(2.116)
Normalization
Evaluating the norm from the inner product of the eigenfunctions with respect to the weight
function w(x) = 1 over the interval yields
> w(x):=1:unprotect(norm):norm:=sqrt(Int(phi[n](x)ˆ2*w(x),x=0..b));norm:=value(%):
norm :=
b
0
cos
λ
n
x
2
dx (2.117)
Substitution of the eigenvalue equation simplifies the preceding equation:
> norm:=radsimp(subs(cos(sqrt(lambda[n])*b)=sqrt(lambda[n])/
h*sin(sqrt(lambda[n])*b),norm));
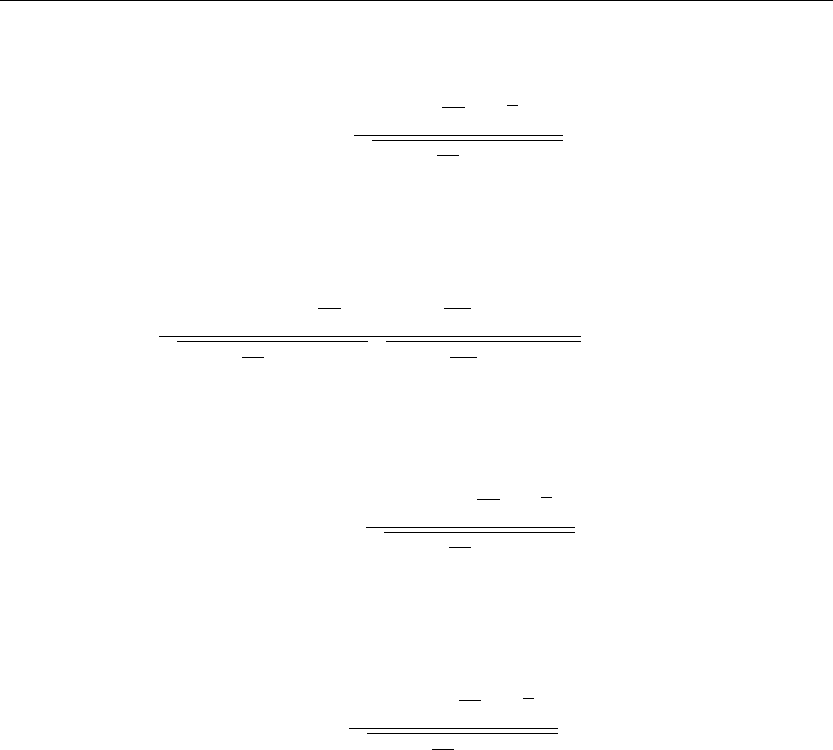
norm :=
1
2
√
2
sin
√
λ
n
b
2
+bh
h
h
(2.118)
Sturm-Liouville Eigenvalue Problems and Generalized Fourier Series 107
Orthonormal eigenfunctions
> phi[n](x):=phi[n](x)/norm;phi[m](x):=subs(n=m,phi[n](x)):
φ
n
(x) :=
cos
√
λ
n
x
√
2h
sin
√
λ
n
b
2
+bh
h
(2.119)
Statement of orthonormality
> Int(phi[n](x)*phi[m](x)*w(x),x=0..b)=delta(n,m);;
b
0
2 cos
√
λ
n
x
h
2
cos
√
λ
m
x
sin
√
λ
n
b
2
+bh
h
sin
√
λ
m
b
2
+bh
h
dx = δ(n, m) (2.120)
Generalized Fourier series expansion
> f(x):=Sum(F(n)*phi[n](x),n=1..infinity);f(x):=‘f(x)’:
f(x) :=
∞
n=1
F(n) cos
√
λ
n
x
√
2h
sin
√
λ
n
b
2
+bh
h
(2.121)
Fourier coefficients
> F(n):=Int(f(x)*phi[n](x)*w(x),x=0..b);F(n):=‘F(n)’:
F(n) :=
b
0
f(x) cos
√
λ
n
x
√
2h
sin
√
λ
n
b
2
+bh
h
dx (2.122)
This is the generalized series expansion of f(x) in terms of the “complete” set of eigenfunctions
for the particular Sturm-Liouville operator and boundary conditions over the interval.
DEMONSTRATION: Develop the generalized series expansion for f(x) = 1 −x over the
interval I ={x |0 <x<1} in terms of the preceding eigenfunctions for h = 1. We assign the
system values
> a:=0;b:=1;h:=1;f(x):=1−x;
a := 0
b := 1
h := 1
f(x) := 1 −x (2.123)
