Артамонов Д.В., Семенов А.Д. Основы теории линейных систем
Подождите немного. Документ загружается.

71
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
×
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
0
0
0
22
2111
c
a
aa
c
V
Выполняя перемножение матриц, найдем, что
V
cac
=
⎛
⎝
⎜
⎞
⎠
⎟
11
00
.
Ранг матрицы
V равен 1, следовательно рассматриваемая система не вполне
наблюдаема и зная из эксперимента
y
невозможно вычислить (наблюдать) коор-
динату
x
2
.
2.4. Понятие управляемости многомерной системы
Понятие управляемости связано с переводом системы посредством
управления из одного состояния в другое. Пусть в пространстве состояний
X за-
даны два подмножества XΓ
1
⊂ и XΓ
2
⊂ . Рассматриваемая система будет
управляемой, если существует такое управление
(
)
T
k
UUUt ),...,(
21
=U , опреде-
ленное на конечном интервале времени0
≤
≤
t
T , которое переводит систему в
пространстве
X из подмножества Г
1
в подмножество Г
2
.
Возможны частные случаи управляемости когда:
1. Пространство состояний
Х ограничено замкнутой областью;
2. В процессе управления осуществляется переход из подмножества
Г
1
в за-
данную точку пространства состояний;
3. В процессе управления осуществляется переход из заданной точки про-
странства состояний в заданное подмножество
Г
1
;
4. В процессе управления осуществляется переход из окрестности одной
точки пространства состояния в окрестность другой точки.
В случае неполной управляемости размерности подобласти
Г
1
меньше раз-
мерности пространства состояния.

72
Кроме этого, управление может происходить при ограничениях, наклады-
ваемых на управляющие и управляемые переменные, что усложняет определение
управляемости. В общем случае задача управляемости не разрешена до настояще-
го времени. Критерии управляемости разработаны только для частных случаев
управления линейными системами.
Для линейной стационарной системы можно записать:
,BuAx
x
+=
d
t
d
(2.41)
где матрицы
А и В постоянны.
При отсутствии ограничений в пространстве состояний и пространстве
управлений, управляемость зависит только от коэффициентов матриц
А и В.
Для управляемой системы справедливо следующее определение. Если для
произвольно заданных
0
x и
1
x , существует управление )(
t
u , переводящее сис-
тему (2.41) за некоторое время
tt
10
−
из состояния
0
xx =)(
0
t в состояние
1
xx =)(
1
t , то система называется вполне управляемой.
Пусть решение уравнения (2.41) задано в виде суммы общего решения од-
нородного уравнения
св
x
и частного решения
в
x неоднородного уравнения
всв
xxx
+
=
. (2.42)
Для управляемости системы необходимо чтобы решение (2.41) было устой-
чивым, что будет выполняться в том случае если:
0lim
=
∞←
св
t
x . (2.43)
Следовательно, для оценки управляемости системы можно ограничится
рассмотрением статических режимов. В этом случае исходная система уравнений
преобразуется к виду:
A
x
B
u
+
=
0 (2.44)
В том случае если размерность вектора )(
t
u больше или равна размерности
вектора )(
t
x , то по завершении управления, когда вектор
1
xx =)(
1
t система (2.41)

73
будет иметь единственное решение в то и только том случае если ранг матрицы
В
равен n. Если размерность вектора )(
t
u меньше размерности вектора )(
t
x , то не-
обходимое и достаточное условие полной управляемости по Калману примет вид:
nRank =
−
)( B)B)...(AB(AB)(A
1n2
, (2.44)
где
[
]
)BB)...(AB(AB)(AU
1n2 −
= - матрица управляемости.
В противном случае система не вполне управляема. Причем степень не-
управляемости может быть по величине
q равной
))( BB)...(AB(AB)(A
1n2 −
−= Ranknq (2.45)
В качестве примера рассмотрим критерий управляемости двигателя посто-
янного тока с двухзонным регулированием (одновременное регулирование, как
по цепи якоря, так и по цепи возбуждения).
Система уравнений для рассматриваемого случая будет выглядеть:
.
;
;
213
3212
2
11
1
J
xkIxkI
d
t
dx
L
xkIRxxku
dt
dx
L
xRu
dt
dx
bnn
bnn
b
b
+
=
−−−
=
−
=
ω
Или после преобразований
;
00
0
0
;
0
00
;
;
;
22
11
3231
232221
11
232131
3
222323222121
2
111111
1
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
+=
+++=
+=
b
b
aa
aaa
a
xaxa
dt
dx
ubxaxaxa
dt
dx
ubxa
dt
dx
BA
Запишем выражение для матрицы
U, в соответствии с формулой (2.44).
74
U
b
b
a
aaa
aa
b
b
a
aaa
aaa
a
aaa
aa
b
b=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
×
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
×
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
×
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
11
22
11
21 22 23
31 32
11
22
11
21 22 23
31 32 33
11
21 22 23
31 32
11
22
0
0
00
00
0
0
0
00
00 00
0
0
0
00
После перемножения матриц и вычисления ранга получим, что
R
an
k
U
()= 3
, т. е. двигатель постоянного тока при двухзонном регулировании
является вполне управляемым. Самостоятельно можно убедиться, что при раз-
дельном управлении двигателем по цепи якоря, или цепи возбуждения система
также будет управляемой.
Управляемость двигателя постоянного тока предполагает, что в результате
соответствующего изменения напряжения возбуждения или якоря можно полу-
чить любые, наперед заданные
значения обобщенных координат двигателя (тока,
скорости и угла поворота) из области их допустимых значений.

75
3. УСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ
3.1. Устойчивость систем в пространстве состояний.
Первая теорема Ляпунова.
Пусть система управления описывается нелинейными дифференциальны-
ми уравнениями в форме Коши:
).(
);(
);,(
xu
ux,y
fu,x,
x
ψ
ϕ
=
=
=
tF
dt
d
(3.1)
Так устойчивость является внутренним свойством системы, то на нее не
оказывают влияние не управляющие, не возмущающее воздействия.
Кроме того, ограничимся рассмотрением устойчивости стационарных сис-
тем, для которых все ее параметры не зависят от времени.
С учетом этих допущений исходную систему можно представить в виде:
dx
d
t
Fxt= (,). (3.2)
Решение этого векторного дифференциального уравнения при некоторых
начальных условиях )(
0
tx имеет вид:
).(t
0
xx
=
Полученное решение описывает траекторию движения системы в про-
странстве состояний, а само движение называется невозмущенным движением.
Если теперь решить систему при других начальных условиях
)(
~
0
tx , откло-
няющихся от
)(
0
tx на незначительную величину
δ
, то ее решение будет назы-
ваться возмущенным движением и запишется в виде:
).(
t
1
xx
=

76
Введём отклонение координат
01
xxx
−
=
Δ
‚ характеризующее разность
между возмущенным и невозмущенным движениями системы. Выражая
1
x через
0
x и xΔ , после подстановки его в (3.2) получим дифференциальное уравнение
системы записанное для отклонений:
).()(
)(
0
xxx
x
0
FF
d
t
d
−Δ+=
Δ
(3.3).
Это уравнение возмущенного движения. Его тривиальное решение 0
=
Δ
x
соответствует невозмущенному движению, так как в этом случае
1
xx
0
=
.
Начальные значения
)(
0
txΔ
носят название возмущений. Решение уравне-
ния (3.3) при Δ
x
≠
0 представляет собой возмущенное движение.
А. М. Ляпунов дал следующее определение устойчивости. Невозмущенное
движение называется устойчивым по отношению к переменным
x
, если при вся-
ком заданном положительном числе А
2
, как бы мало оно не было, можно вы-
брать другое положительное число
δ
2
так, что для всех возмущений, удовлетво-
ряющих условию:
δ
≤
Δ
)(
0
tx (3.4)
возмущенное движение (3.3) будет в промежутке времени
tt
0
≤≤∞ удовлетво-
рять неравенству:
At
≤
Δ
)(
0
x (3.5)
Если с течением времени )(
t
x
Δ
стремится к нулю, то система называется
асимптотически устойчивой.
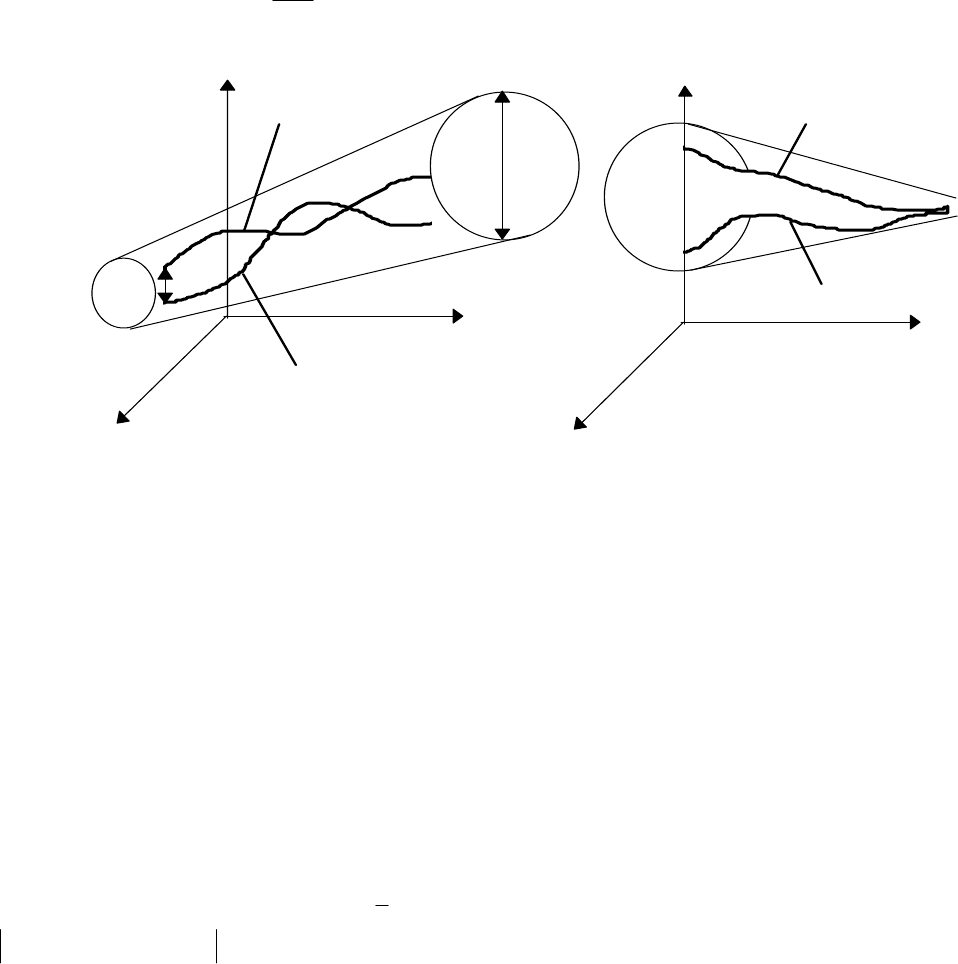
Геометрическая интерпретация устойчивости показана на рис. 3.1.
Отметим, что условие устойчивости, доказанное Ляпуновым будет спра-
ведливо, если имеется возможность перехода к дифференциальным уравнени-
ям записанным в отклонениях (3.3). Очевидно, что такой переход возможен толь-
ко в случае линейных или линеаризуемых систем, причем линеаризация осуще-
77
ствляется в окрестностях точки невозмущенного движения при малых отклонени-
ях
Δ
x
.
Линеаризуя (3.3) , можно записать:
dx
dt
ax tx x x
i
ij j n
j
n
=+
=
∑
ψ
( ; , ,..... )
12
1
in= 12, ,.... (3.6)
x
3
x
3
xt
0
()
xt
0
()
A
δ
x
1
xt
1
()
x
1
xt
1
()
x
2
x
2
Устойчивое движение Асимтотически устойчивое движение
Рис 3.1.
Первая теорема Ляпунова дает определение достаточное условие устой-
чивости при малых отклонениях системы от ее невозмущенного движения, или
определение устойчивости " в малом " и формулируется следующим образом:
Пусть все корни характеристического уравнения линеаризованной системы
(3.6), без учета второго слагаемого
ψ
in
tx x x(; , ,... )
12
, имеют отрицательную дей-
ствительную часть и все функции
ψ
in
tx x x( ; , ,... )
12
удовлетворяют условию
ψ
α
ini
i
n
tx x x M x( ; , ,... )
12
2
1
1
2
≤
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
=
+
∑
, причем
M
- постоянная и
α
> 0
.
Тогда тривиальное решение системы (3.2) устойчиво.
Наиболее просто можно судить об устойчивости линейных систем.
78
Для них понятие устойчивости " в малом " и устойчивости в большом,
или абсолютной устойчивости совпадают. Если система устойчива "в малом", то
она устойчива и в большом.
В случае нелинейной системы с гладкими нелинейностями Ляпуновым
были доказаны следующие теоремы:
1. Если характеристическое уравнение линеаризованной системы имеет
все корни с отрицательными вещественными частями
, то реальная система бу-
дет также устойчивой. Малые нелинейные члены не могут нарушить устойчи-
вость системы.
2. Если характеристическое уравнение линеаризованной системы имеет хо-
тя бы один корень с положительной вещественной частью, то реальная система
также будет неустойчивой. Малые нелинейные члены не могут сделать ее устой-
чивой.
3. При наличии нулевых
или чисто мнимых корней, поведение реаль-
ной системы не всегда даже качественно определяется ее линеаризованными
уравнениями. Малые нелинейные члены могут коренным образом изменить ха-
рактер переходного процесса.
Следует иметь в виду что данные теоремы Ляпунова сформулированы
для устойчивости " в малом " и для нелинейных систем с гладкими нелинейно-
стями, которые могут
быть линеаризованы путем разложения в ряд Тейлора.
Для определения устойчивости нелинейных систем с нелинейными ста-
тическими характеристиками, имеющими точки разрыва, или для определения
устойчивости нелинейных систем "в большом" используется прямой метод
Ляпунова, или вторая теорема Ляпунова.
3.2 Устойчивость линейных систем.
Алгебраические критерии устойчивости

79
Для линейной системы уравнения её движения в пространстве состоя-
ний можно представить в следующем виде:
AX
X
=
dt
d
, (3.7)
где
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
nnnn
n
n
aaa
aaa
aaa
L
LLLL
K
K
21
22221
11211
A
.
Квадратная матрица размером
nn
×
Или в развернутой форме:
nnnnn
n
nn
nn
XaXaXa
d
t
dX
XaXaXa
dt
dX
XaXaXa
dt
dX
K
KKKKKKKKKKKKKK
K
K
++=
++=
++=
2211
2222121
2
1212111
1
(3.8)
Из математического анализа известно, что любое частное решение одно-
родной системы (3.8) вида:
Xe
i
t
i
=
λ
, (3.9)
будет обращаться в тождество, где
λ
i
произвольные числа.
Подставляем в (3.8) частное решение (3.9) и после очевидных преобразо-
ваний получим следующую систему линейных однородных алгебраических
уравнений из которых можно найти
λ
i
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=−++++
=+−++
=++−+
=
+
+
+
−
.0)(
;0)(
;0)(
;0)(
332211
33333232131
23232222121
13132121111
nnnnnnn
nn
nn
nn
xaxaxaxa
xaxaxaxa
xaxaxaxa
xaxaxaxa
λ
λ
λ
λ
K
LLLLL
K
K
K
(3.10)

80
Решая эту систему можно найти
x
i
. Известно, что нетривиальное реше-
ние такой системы будет при условии равенство нулю главного определителя
системы
0
321
33333231
22322221
11312111
=
−
−
−
−
nnnnnn
n
n
n
aaaa
aaaa
aaaa
aaaa
λ
λ
λ
λ
K
KKKKK
K
K
K
(3.11)
Это и будет характеристическое уравнение системы, a
λ
λ
λ
12
, ,....
n
явля-
ются корнями характеристического уравнения.
Получив характеристическое уравнение системы можно определить устой-
чивость по корням этого уравнения. Для этого запишем общее решение системы
(3.8)
XCe
CB i i
t
i
n
i
=
=
∑
λ
1
.
Для устойчивости системы необходимо и достаточно, чтобы
lim
t
CB
X
→∞
=
0
.
Это условие выполняется в случае , если все корни характери-
стического уравнения будут "левыми", т.е. будут иметь отрицательные дей-
ствительные части и располагаться слева от мнимой оси комплексной плоскости.
Непосредственное применение необходимого и достаточного условия, тре-
бующее решение характеристического уравнения, просто лишь для систем перво-
го и второго порядков, менее
удобно в случае третьего и четвертого порядков,
а для систем более высоких порядков является довольно трудоемкой задачей. Од-
нако, чтобы судить о том, удовлетворяет ли линейная система необходимому и
достаточному условию устойчивости, нет надобности находить корни характе-
