Аракелян А.К., Афанасьев А.А. Вентильные электрические машины в системах регулируемых электроприводов. Том 1
Подождите немного. Документ загружается.

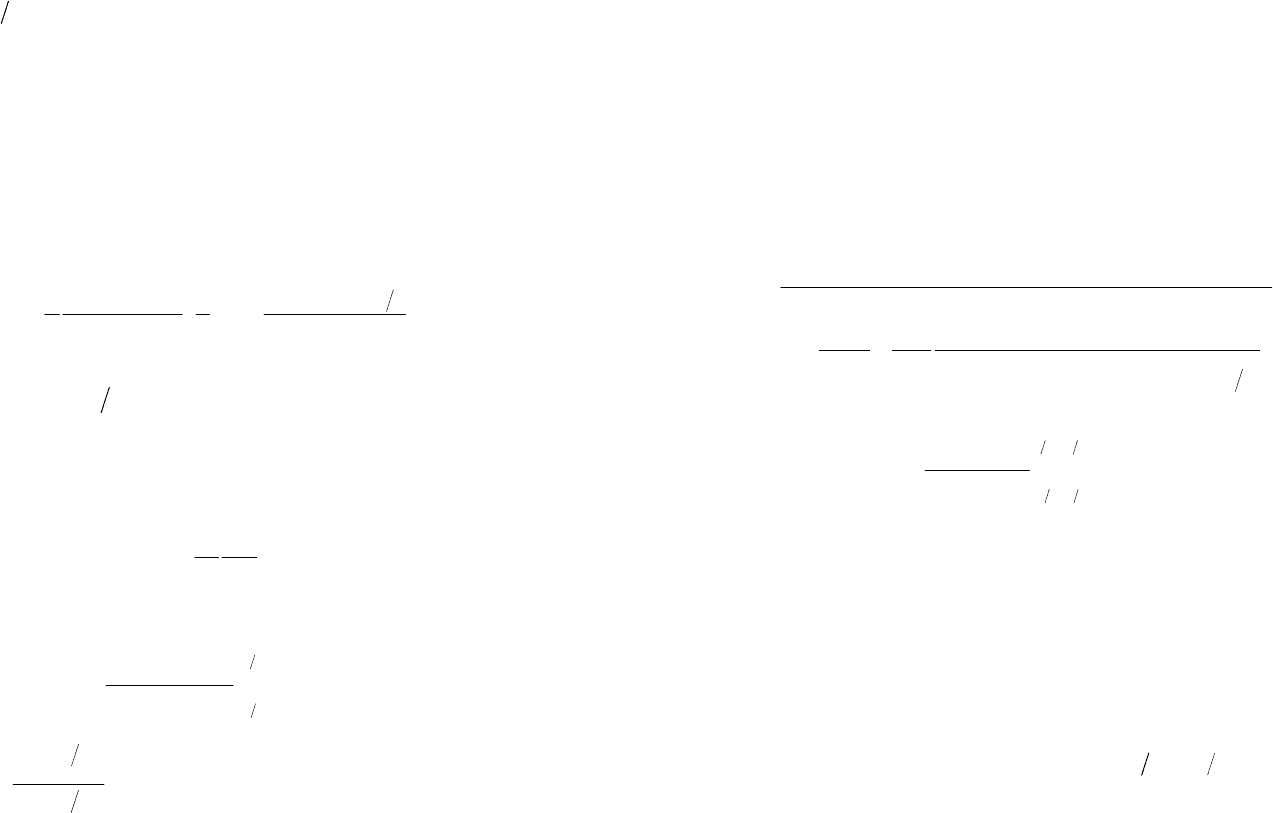
80
81
iiimii
l BBB
,,;
- магнитная индукция, длина и магнитная
ï ðî í èöàåì î ñòü ó÷àñòêà ñ í î ì åðî ì
i магнитопровода.
Элементарные магниты обычно изготавливают в форме
прямых призм, ширина одной из параллельных граней которых
выбирается равной ширине наружной грани шихтованного ярма
ротора. Ротор с приклеенными магнитами и текстолитовыми
прокладками в межполюсных зонах подвергается шлифовке,
которая придает его наружной поверхности форму, близкую к
цилиндрической. Переменная высота образовавшегося магнитного
слоя может быть представлена рядом
,
pp
м0м
1
minmax
1212
6cos1
2
1
24
)(
k
k
kk
kx
DD
hxh
(1.200)
где
min pmax pмmaxрмм0
, , DDDDDh ,2
- диаметры ротора по
наружной поверхности магнитов, описанной и вписанной
окружностей наружного многоугольника поперечного сечения
ярма ротора.
Остаточный момент находится по известной зависимости
,
Wp
M
(1.201)
где W - энергия МП в воздушном зазоре и магнитах машины,
определяемая по формуле [186]
,
2
23
2
0
2min
dxB
Bpkkl
W
r
(1.202)
где
0
2
1
k
l
k
i
iii
min
; B
r
- остаточная индукция магнитов.
При скошенных полюсных зонах, имеющих форму трапеции с
высотой l и основанием b
p
(рис.1.18,б), расчет магнитной энергии
требует обращения к формуле с двукратным интегрированием, в
которой у одного из интегралов верхний и нижний пределы являются
не числами, а функциями одной из координат, например, )(x
.
Поскольку использование такой формулы усложняет численные
расчеты, то целесообразно область интегрирования в плоскости х,
у подвергнуть преобразованию
,;
yx ctg
c
функциональный определитель (якобиан) которого
01
J
(
c
-
угол скоса полюсной зоны).
В новых координатах (
, ) полюсная зона будет иметь форму
прямоугольника с размерами
p
bl
. В результате этогоо
преобразования формулы (1.200), (1.202) принимают вид
;
)(2cos
1)(
)()(
10
0
min
1
k
k
tk
h
k
hH
B
c
м
м
мc
ctg
(1.203)
.
2
2
2
23
2
0
2min
l
l
r
ddB
Bkk
W
(1.204)
Для определения
)(
м
h
нужно воспользоваться выражением
(1.200), заменив в нем х на
.
По предложенным формулам рассчитывался остаточный
момент трехфазного шестиполюсного бескорпусного ВД с
диаметром фланца 115 мм, высотой оси вращения 50 мм, который
выполняется на три длины, соответствующие моментам 1,7; 4,7;
7,0 Нм. Его параметры в базовом варианте 1 следующие: магниты
- самарий-кобальтовые (
мм;
мо
5,3
h кА/м;
c
480
H Тл;7,0
r
B
;49мм
maxp
D мм;
pmin
4,48
D
мм;
м
56
D
количество наружных
граней у ярма ротора - 18);
мм;
min
75,0
pZt 2
11
27/6=4,5;
q=1,5; пазы на статоре полузакрытые с относительным раскрытием
;36,068,6/4,2/
1
tb
ш
длина пакета статора (вторая) l=100 мм.
Базовый вариант 2 выполняется в тех же габаритах, но с целым
числом пазов на полюс и фазу (q=2; z
1
=36). При изготовлении
опытных образцов ВД элементарные магниты намагничивались в
импульсном режиме до закрепления на ярме ротора.
На рис.1.19 приведены кривые остаточного момента в функции
82
83
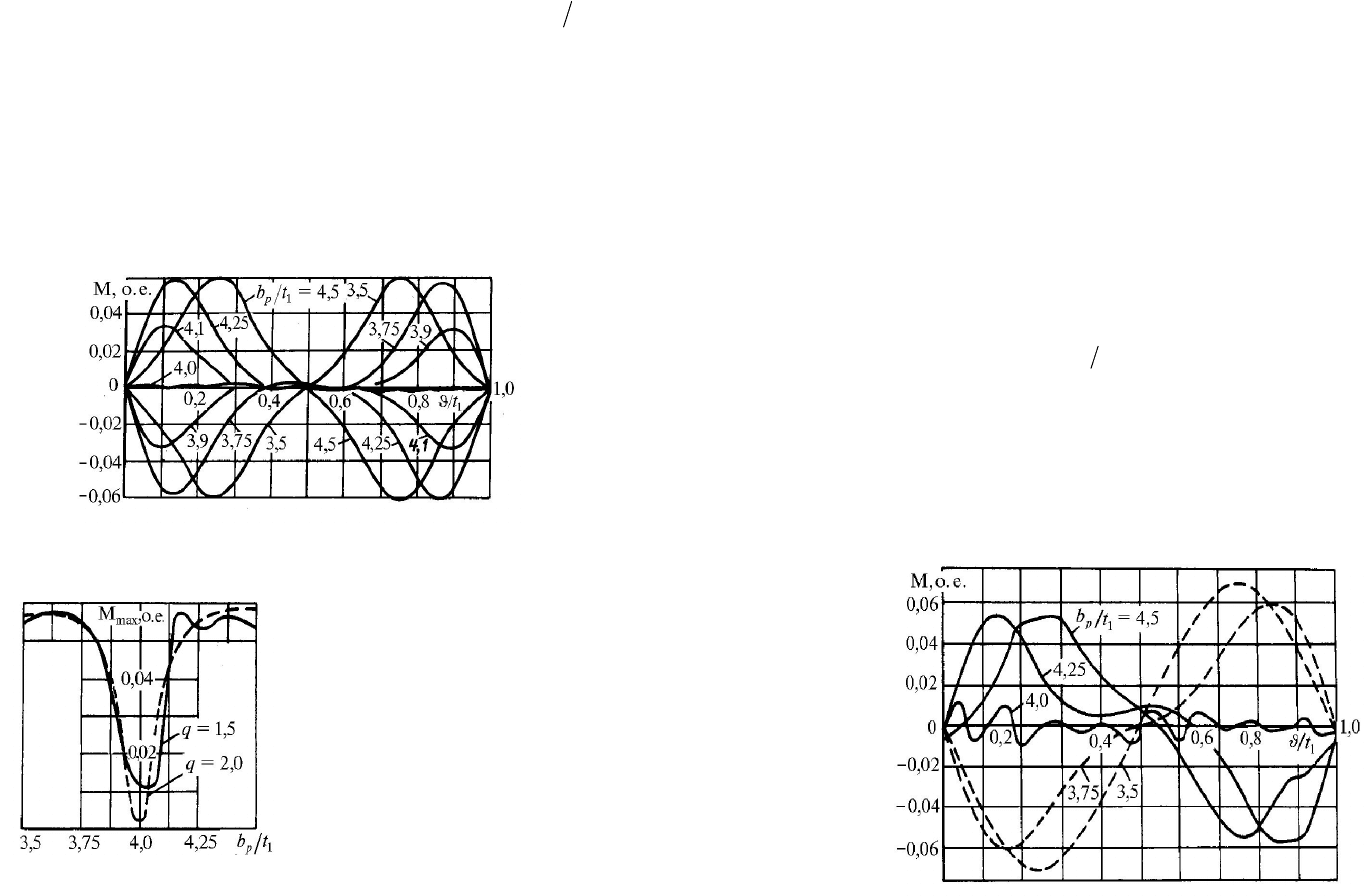
Рис.1.20. Максимум остаточного
момента в функции ширины
полюсной зоны
углового положения ротора для базового варианта 2 с различной
относительной шириной полюсной зоны (
1
tbb
pp
),
рассчитанные на ЭВМ по формулам (1.199)-(1.202), из которого
видно, что чувствительность максимума остаточного момента к
параметру
p
b
проявляется в виде остро выраженного резонанса:
она резко возрастает при целом значении
p
b
. Как следует из
рис.1.20, при отклонении
p
b
от целого значения всего на 2,5% (или
на 0,67 мм для варианта 1) максимум момента возрастает в
вариантах 1 и 2 соответственно в 2,6 и 13 раз по сравнению с его
значениями при целом
p
b
, составляющими соответственно 1,29 и
0,27% номинального момента ВД.
Для оптимальной ширины
полюсной дуги максимум
остаточного момента при целом
q (q=2) в 4,8 раза меньше, чем
при дробном q (q=1,5). В
практике изготовления дви-
гателя с кусочно-составным
(мозаичным) принципом форми-
рования магнитного слоя ротора
необходимая ширина геометри-
ческой полюсной зоны должна
выдерживаться с требуемой
точностью благодаря специаль-
ной механической обработке
Рис. 1.19. Остаточный момент в функции
углового положения ротора при 2
q
магнитов на собранном роторе. Ширина фактической (физической)
полюсной зоны может быть больше геометрической за счет эффекта
выпучивания МП [240]. В принятых обозначениях под параметром
p
b
следует понимать относительную ширину именно физическогоо
полюса.
Кривые на рис.1.21, показанные сплошными линиями,
соответствуют базовому варианту 1. Видно, что при дробном
p
b
число пазов q=1,5 вызывает незначительное снижение максимума
момента (примерно на 10%), кривые становятся более
специфичными, но их характер в принципе сохраняется. Однако
для целого значения
p
b
при переходе от варианта 2 к варианту 1
наблюдается, как отмечалось, значительный рост (в 4,8 раза)
максимума момента до 0,0129M
н
. Кривые (рис.1.21), показанные
штриховыми линиями, соответствуют варианту 2 и пазам статора
с большим открытием (
5,0
1
tb
ш
). Сравнивая эти кривые с
предыдущими того же варианта (рис.1.19), следует отметить рост
максимального значения момента (примерно на одну треть) и
форму, близкую к синусоиде, у кривой с
p
b
=3,5 или 4,5.
Были выполнены также соответствующие расчеты для ротора
с постоянной толщиной магнитного слоя
minpmaxp
DD
, которые
показали, что при дробном
p
b
(и при
p
b
, равном целому числу для
Рис.1.21. Остаточный момент в функции углового
положения ротора при дробном (--) и целом (- - -) q

84
85
q=1,5) грани на поверхности ярма ротора практически не влияют
на остаточный (реактивный) момент (максимальное расхождение
с предыдущими кривыми не превосходит 5%). Только лишь для
кривых с целым значением
p
b
и q характерно качественноее
различие, которое, однако, практического значения не имеет,
поскольку остаточные моменты при таких b
p
ничтожно малы (не
превышают 0,3 % номинального рабочего момента). Измерения
остаточного момента у опытного ВД с q= 1,5 и цилиндрической
(гладкой) наружной поверхностью ярма ротора подтвердили эти
расчетные результаты.
Во всех предыдущих расчетах полагали
const
c0c
HH
для
любых точек полюсных зон. Целесообразно оценить влияние
пространственной неоднородности коэрцитивной силы
элементарных магнитов на остаточный момент. Рассмотрим два
варианта испытательного воздействия:
- имеет место неоднородность только по оси х (рис. 1.26), при
этом
)sincos1(
210
xnkxnkHH
xxcc
, (1.205)
- неоднородность аналогичного характера имеет место только
по оси y, при этом
)sincos1(
210
ynkynkHH
yycc
, (1.206)
где
)()(
2
yxyx
T
.
На рис.1.22 построены кривые остаточного момента,
полученные с помощью формул (1.199)-(1.202), (1.205) для
4
p
b
;
;2
x
T
n'=3 (по ширине полюса располагались три ряда
элементарных магнитов); k
1
= k
2
= k = var, которые показывают, что
неоднородность первого вида может в принципе вызвать
остаточный момент с максимальным значением такого же порядка,
как и при неоптимальной ширине полюсной зоны (
p
b
- дробноее
число) в случае с
const
c
H
. Неоднородность
c
H
по оси y являетсяся
практически не опасной, так как она, как показывает анализ формул
(1.199)-(1.202), (1.206), при k
1
= k
2
= k увеличивает остаточный
момент лишь на множитель (1+k
2
), близкий к единице. Поэтому,
если ширина полюсной зоны оптимальна, то остаточный момент
сохраняется малым и при наличии указанной неоднородности.
Из-за резко выраженной критичности остаточного момента к
оптимальной ширине полюсной зоны, технологических трудностей
выдерживания этой ширины, ограниченной предсказуемости
параметров пространственной неоднородности магнитов
целесообразна такая конструкция ВД, которая позволяла бы
направленно влиять на значение остаточного момента при действии
указанных факторов. Опыт показывает, что такие возможности
предоставляются при составном роторе, состоящем, например, из
двух равных по длине частей, из которых одна жестко фиксирована
на валу, а угловое положение другой определяется из условия
получения минимума остаточного момента. Зубцы статора диктуют,
как видно из рис.1.19 и 1.21, взаимный сдвиг обеих частей ротора
на половину зубцового деления статора, опытные же данные
показывают, что при сдвиге на 0,2t
1
обеспечивается снижение
остаточного момента с 0,047М
н
до минимального значения 0,017М
н
.
Специфический размер сдвига частичных роторов указывает, что
фазовая ориентация их магнитных полей определяется не только
геометрией магнитной цепи, но и характером пространственного
распределения вектора намагниченности. Следует также заметить,
что поскольку периодические кривые остаточного момента
частичных роторов не обладают симметрией третьего рода
)()2( xfTxf
, то при их сложении с взаимным сдвигом число
пульсаций момента (число фиксаций ротора) на интервале
1
0 t
удваивается. Так, у опытного двигателя с z
1
=27 число
Рис. 1.22. Влияние на остаточный момент тангенциальной
неоднородности магнитов при дробном (-) и целом (- - -) q

86
фиксаций ротора за один оборот увеличивается с 27 (при отсутствии
сдвига частичных роторов) до 54 (при наличии сдвига).
Опытные измерения и расчеты остаточного момента у
двигателей, выполненных со скосом полюсных зон (q=1,5) и пазов
(q=2)
1
на одно зубцовое деление статора, не выявили преимущества
этого способа борьбы с "залипанием" ротора по сравнению с
выдерживанием целого значения
p
b
. Однако у двигателя с q=2
(z
1
= 36) при скосе пазов статора на два зубцовых деления опыт
показал существенное снижение остаточного момента почти до
такого же значения, как и при настроенном развороте частичных
роторов. Обнаруженный эффект можно объяснить тем, что
выполненный скос пазов не настроен на пространственный период
основной волны неоднородного намагничивания магнитов, который
оказался не равным зубцовому делению статора. В этом случае,
как известно [240], c увеличением скоса пазов уменьшаются
амплитуды зубцовых гармоник момента.
При сравнительно большом числе пазов статора, приходящихся
на один полюс, указанный скос не вызывает существенного
снижения использования двигателя, так как коэффициент скоса на
рабочей гармонике остается достаточно высоким (в рассмотренном
варианте k
с1
=0,955).
Выводы
1. Для снижения остаточного момента ВД целесообразны
следующие мероприятия: составная конструкция ротора и двойной
скос пазов статора соответственно в бескорпусном и корпусном
исполнениях ВД; строгое выдерживание оптимальной ширины
полюса с отклонением не более 2,5%, целое число пазов (q),
минимальное возможное раскрытие пазов статора.
2. Огранение наружной поверхности ярма ротора, диктуемое
технологией закрепления магнитов, практически не влияет на
значение остаточного момента.
1
Опытный образец двигателя в варианте 2 (q=2; 2p=6, Z
1
=36) выполнен в
корпусном исполнении, позволяющем производить сдвиг пазов статора.
87
Г л а в а в т о р а я
РАСЧЕТ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ
МАШИНАХ СИНХРОННОГО ТИПА
МОДЕРНИЗИРОВАННЫМ МЕТОДОМ УДЕЛЬНОЙ
МАГНИТНОЙ ПРОВОДИМОСТИ
2.1. Общие замечания
Электрические машины синхронного типа, специально
предназначенные для совместной работы со статическими
преобразователями частоты (вентильные электрические машины),
отличаются большим конструктивным разнообразием в
зависимости от типа используемого преобразователя частоты,
функционального назначения электроустановки, диапазона
регулирования частоты вращения, способа возбуждения, типа
постоянных магнитов и других факторов.
Особенно широкое применение вентильных машин характерно
для электропривода металлорежущих станков и роботов [120, 179].
Такие электроприводы отличаются, в частности, повышенной
надежностью из-за отсутствия механического коллектора и
пониженными эксплуатационными расходами.
В электроприводе главного движения металлорежущих станков
используются вентильные электродвигатели с электромагнитным
возбуждением мощностью 15...180 кВт с диапазоном регулирования
скорости вращения 1:1000, в том числе с постоянством мощности
вверх от номинальной 1:4 [154]. Такой же тип электрической
машины применен в серии вентильных двигателей мощностью
200...3150 кВт при максимальных частотах вращения
100...1000 об/мин [165].
Для робототехнических комплексов и механизмов подачи
металлорежущих станков наиболее перспективны электроприводы
с двигателями, имеющими возбуждение от высокоэнергетических
постоянных магнитов. Эти электроприводы могут быть полностью
бесконтактными, с высоким уровнем удельного момента и
показателей быстродействия.
88 89
В настоящей главе рассматриваются методы и особенности
электромагнитного расчета вентильных машин с электро-
магнитным и магнитоэлектрическим возбуждением.
Приводятся краткие сведения о принципиальных особенностях
конструктивного исполнения этих машин с точки зрения увязки
его со спецификой электромагнитных расчетов.
2.2. Расчет магнитного поля явнополюсной электрической
машины с электромагнитным возбуждением
Магнитное поле электрической машины может быть
определено решением уравнений Максвелла, представленных в
дифференциальной или интегральной формах.
Уравнения второй формы положены в основу известных методов
расчета магнитного поля: магнитной проводимости [96],
проводимостей зубцовых контуров [135]. Они позволяют с тем или
иным приближением учесть основные физические факторы:
нелинейность магнитной цепи, двухстороннюю зубчатость воздушного
зазора, дискретность распределения проводников обмоток.
Применительно к конкретным типам и особенностям работы
электрических машин актуальны разработка новых и
совершенствование известных методов расчета поля. Так, для
электрических машин автономной энергетики и электропривода,
работающих совместно со статическими преобразователями
частоты, целесообразны методы расчета магнитного поля и
индуктивных параметров, позволяющие с приемлемыми для
практики точностью и затратами машинного времени учесть, в том
числе в переходном режиме, все или часть перечисленных
физических факторов [219]. Такие машины имеют высокую степень
насыщения магнитной цепи и, в частности, малые частоты
вращения на нижней границе рабочего диапазона, при которых на
качество вращения существенное влияние оказывают зубчатость
воздушного зазора и дискретность распределения проводников
обмоток.
В настоящем разделе рассматриваются особенности
численного расчета магнитного поля в явнополюсной
электрической машине методом магнитной проводимости при
раздельном учете всего спектра проводимостей различных
зубчатых структур воздушного зазора: зубцов статора и ротора,
полюсов индуктора, неравномерности зазора между полюсными
наконечниками и окружностью расточки якоря.
Излагаемая ниже методика может быть использована для
расчета магнитного поля других типов электрических машин с
различными видами пазов и зубчатых образований, например,
асинхронных, редукторных.
2.2.1. Исходные допущения и принципиальные особенности
расчета
Расчет поля производим при следующих основных
допущениях:
1) магнитное поле в воздушном зазоре плоскопараллельно;
2) насыщение зубцовой зоны не оказывает влияния на
конфигурацию магнитного поля в воздушном зазоре;
3) магнитное поле в зазоре является полем взаимоиндукции.
(В соответствии с принятым методом расчету подлежит нормальная
(радиальная) составляющая индукции в середине локального
воздушного зазора между условно гладкими поверхностями статора
и ротора. При таком допущении для каждой силовой трубки
магнитное напряжение зазора может быть выражено через
произведение индукции в среднем сечении и удельного магнитного
сопротивления трубки, которое при допущении (2) является
функцией только взаимного положения статора и ротора). Поле
рассеяния по коронкам зубцов может рассчитываться отдельно;
4) воздушный зазор при расчете удельной магнитной
проводимости принимается равным сумме равномерного
воздушного зазора и дополнительных зазоров, обусловленных
раздельно зубчатостью статора при гладком роторе и зубчатостью
ротора при гладком статоре;
5) магнитные поля рассеяния обмоток якоря и успокоительной
не зависят от насыщения магнитной цепи.
Будем считать, что точки зазора, в которых определяется
индукция, принадлежат двум осям: неподвижной (жестко
привязанной к статору, с началом отсчета на магнитной оси фазы А)
90 91
и вращающейся x (жестко привязанной к ротору, с началом отсчета
на оси d). Каждой счетной точке с координатами
k
или x
k
(k = 0,1,2,...
nz
1
; z
1
- число пазов якоря) соответствует значение индукции B
k
(рис.2.1). Связь между координатами
k
и x
k
выражается
равенством:
,2 ppx
kkk
1
(2.1)
где
k
1
- единичная ступенчатая функция;
p - число пар полюсов,
d
t
0
р0 , (2.2)
ð
- электрическая частота вращения ротора.
Магнитное напряжение в k-й точке воздушного зазора равно:
0
kkk
BF , (2.3)
где
4
1i
k
i
mk
, (2.4)
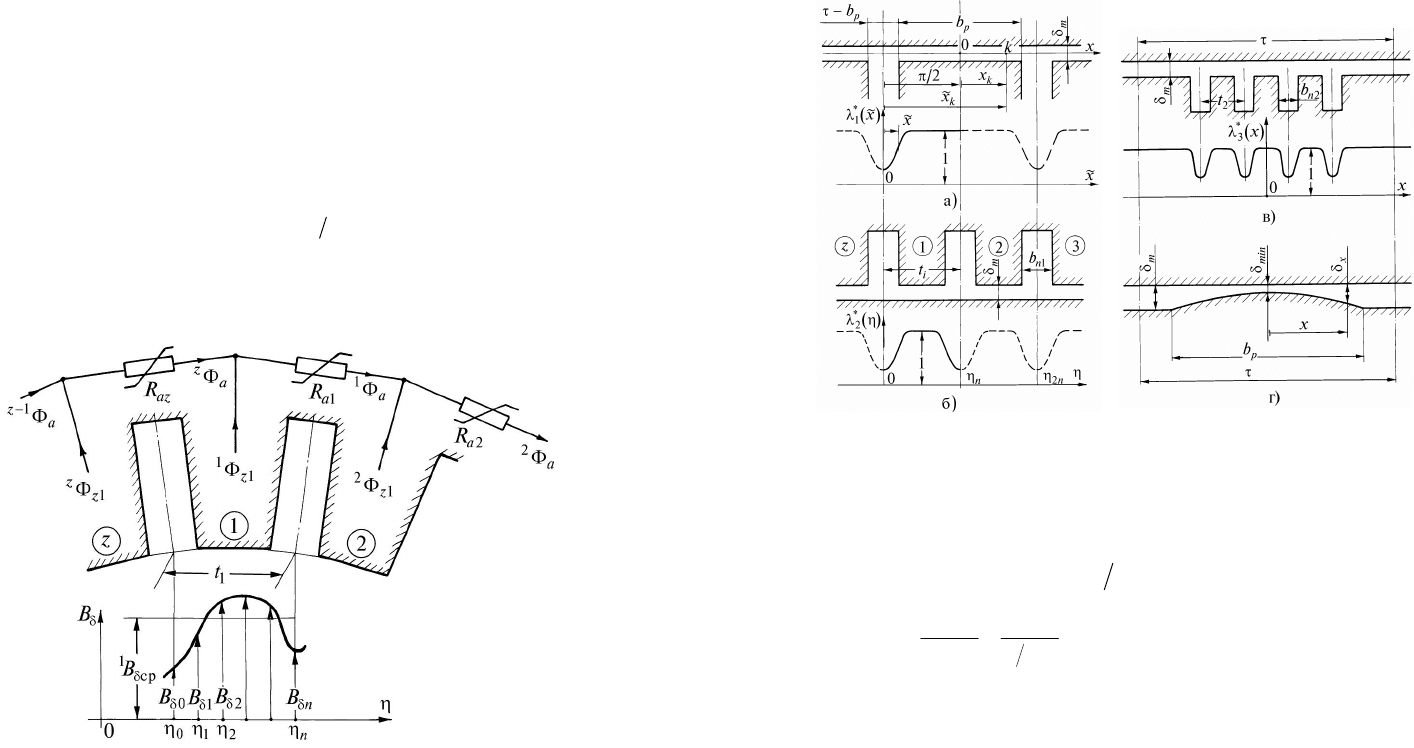
Рис. 2.1. Расчетная схема якоря
k
i
- составляющие длины воздушного зазора в k-й точке,
обусловленные четырьмя зубчатыми структурами зазора.
Полюса индуктора образуют первую зубчатую структуру (i=1).
Они могут рассматриваться в виде больших зубцов, отделенных от
якоря равномерным зазором
m
, а друг от друга - пазами конечной
или бесконечной глубины и шириной, равной расстоянию между
полюсными наконечниками (рис.2.2,а).
В этом случае
mkmk
x
~
1
1
, (2.5)
где
m
k
max
k
k
xx
x
1
~
~
~
11
1 - относительная удельная магнитная
проводимость зазора. Она является периодической функцией,
полученной в результате сплайновой аппроксимации и
периодизации функции удельной относительной магнитной
Рис.2.2. Расчет зубчатости воздушного зазора, обусловленной: а - по-
люсными сердечниками индуктора; б - зубцами якоря; в - зубцами на
поверхности полюсных наконечников индуктора; г - неконцентричностью
гладких поверхностей якоря и полюсных наконечников

92 93
проводимости униполярному потоку [44] для средней окружности
воздушного зазора
.2
m
y
.
Зубцы якоря при гладкой поверхности индуктора (рис.2.2,б)
образуют вторую зубчатую структуру (
2
i
). Для нее
mkmk
2
2
, (2.6)
где периодическая функция относительной удельной магнитной
проводимости
*
2
получена в результате сплайновой
аппроксимации и периодизации соответствующей функции,
рассчитанной также для средней окружности воздушного зазора
2
m
y
.
Если ширина зубцов якоря удовлетворяет неравенству
3
mz
b
, то для нахождения функции
*
2
можно
воспользоваться и более простой зависимостью [44].
Зубцы на поверхности индуктора при гладкой поверхности якоря
(рис. 2.2,в) образуют третью зубчатую структуру (
3
i
). Для нее
mkmk
x
3
3
. (2.7)
Периодическая функция
x
3
может быть определена
аналогично предыдущему случаю.
В качестве четвертой зубчатой структуры зазора (
4
i
)
выступает неравномерность зазора между гладкой поверхностью
якоря и полюсными наконечниками индуктора (рис.2.2,г).
Профилированные, небольшой высоты выступы на гладкой
поверхности индуктора рассматриваются как зубцы. Для
параболического характера изменения зазора под полюсами имеем
при 0,
при
.22
;22,2
2
4
pkp
pkppkminmmmin
k
bxb
bxbbx
(2.8)
Формула (2.4) позволяет найти локальные и средние значения
коэффициента Картера:
4
1
1
i
mk
i
k
k
;
dk
i
i
m
cp1
2
0
4
1
2
1
1
;
dxx
b
k
p
p
b
b
i
i
mp
cp
2
2
4
1
2
1
1
,
где
p
b
- ширина полюсного наконечника.
Для синхронной машины типа СД 102-8 с параметрами,
отмеченными ниже, будем иметь
3213,3
1
cp
k
;
5915,1
2
cp
k
.
Коэффициент Картера, рассчитанный для этой машины по
обычной методике [139], основанной на усреднении индукции в
пределах зубцовых делений статора и ротора, составит 1,4684.
Следует отметить, что расчет магнитной проводимости
воздушного зазора с двухсторонней зубчатостью указанным
методом, как показано в [44], принципиально точнее по сравнению
с известной формулой для этой проводимости, содержащей в
качестве сомножителей относительные магнитные проводимости
статора и ротора [96].
Счетные точки выбираются на неподвижной оси
, причем
таким образом, чтобы каждый зубцовый шаг статора содержал n
точек.
Фиксируются зубцовые множества
1
статора:
1
...,,2,1, zS
S
k
; ротора:
2
...,,2,1, zRx
R
i
k
,
.2...,,3,2,1
pi
Первые определяют счетные точки оси
, относящиеся к зубцу
статора с номером S, вторые объединяют точки, относящиеся к
зубцу с номером R и полюсу i ротора. Находятся средние значения
индукции в воздушном зазоре, приходящиеся на конкретные
зубцовые деления статора
)...,2,1(
1
zбSB
S
ср
; ротора
*
2
...,,2,1 zRB
R
ср
и полюсные деления
)2...,2,1(
piB
i
,
ср
.
При расчете магнитного напряжения зубцов полагаем, что
магнитный поток, приходящийся на участки оси
x
в пределах
зубцового деления
21
tt
, полностью входит в зубец на расстоянии
кp
)2(1z
h
от вершины зубца. За
кp
)2(1z
h
принимаем значение одногоо
открытия паза. В соответствии с этим для прямоугольных пазов
определяются три значения магнитной индукции, а затем, по кривой
1
Значения величин
pzz ;;
2
1
определяются пространственным периодомм
магнитного поля.

94 95
намагничивания и значения магнитной напряженности в зубце: на
вершине
вер
z
H
, в критическом сечении
кp
z
H
и у основания зубца
осн
z
H
. Кривую намагничивания стали аппроксимируем сплайнами
третьего порядка. Магнитное напряжение зубцов определяем по
формуле:
крсркрср
zzzzzz
hhHhHF
21
, (2.9)
где
2
1 крверср
zzz
HHH
;
2
2 оснкрср
zzz
HHH
.
Для счетных точек каждого множества
S
k
или
R
i
x
принимаются соответственно одинаковые значения
1z
S
F
или
2z
R
F
.
Магнитное напряжение зубцового слоя для k-й точки
воздушного зазора
21 z
R
z
S
zk
FFF
. (2.10)
Магнитное напряжение ярма якоря находим в соответствии с
расчетной схемой (рис. 2.1), на которой магнитный поток S-го зубца
якоря
.
11
tlB
S
z
S
кр
Потоки
1
zzz
элементов ярма якоря определяются в
соответствии с уравнениями:
1
1
za
A
;
1
1
z
z
a
z
a
z
, (2.11)1)
где
Т
a
z
aaaa
1321
...
,
Т
1
1
1
3
1
2
1
1
1
...
z
z
zzzz
,
11...000
..................
00...110
00...011
11...111
)1()2(321 zazaaaa
rrrrr
A
,
ziRRr
azaiai
...,,3,2,1
,
;
a
i
a
i
ai
Fr
- магнитное сопро-
тивление i-го элемента ярма.
Значения магнитных потоков
a
i
и напряжений
a
i
F
уточняются итерационным методом. При первом просчете
уравнений (2.11) элементы
ai
r
считаем известными. Найденные
значения
a
i
a
i
a
i
a
i
FHB
используются для определения
элементов второго приближения и т.д.
Магнитное напряжение i-го полюса индуктора
2
F
i
, равноее
сумме магнитных напряжений полюсного сердечника
m
i
F
, стыкаа
сердечника с ярмом
m
i
F
и ярма индуктора
aи
i
F
, находитсяся
путем расчета магнитных потоков в трех сечениях полюса: у
основания, в среднем сечении и у полюсного наконечника.
Соответствующая система уравнений, включая уравнения
сплайновой аппроксимации кривых намагничивания стали, решается
относительно магнитных индукций и напряженностей в указанных
сечениях и ярме индуктора, средней магнитной напряженности
полюсного сердечника методом простых итераций (при малых и
средних насыщениях стали) и методом Ньютона (при значительных
насыщениях).
При расчете суммарного тока, сцепленного с контуром
магнитной цепи, стороны которого проходят через воздушный
зазор, предполагаем линейный характер изменения МДС обмотки
в пределах открытия ее пазов. Это касается всех обмоток, в том
числе и возбуждения. Нахождение униполярной составляющей
МДС в данном случае не требуется, так как каждый расчетный
магнитный контур включает в себя две разные счетные точки
воздушного зазора. При обходе такого контура значения
униполярной МДС взаимно компенсируются (их суммарная
величина равна нулю), непрерывность же магнитного потока
учитывается уравнением (2.15). В принципе, для этих контуров
можно не обращаться к понятиям МДС, а пользоваться полными
токами, сцепленными с контурами.
Короткозамкнутую обмотку на полюсах индуктора
представляем в виде двухслойной обмотки, имеющей шаг, равный
зубцовому делению (на участке в пределах полюсного
наконечника), и 1
q .
Основной целью расчета является определение значений
индукции
k
B
в точках воздушного зазора
k
или
k
x
, взятых
соответственно в неподвижных относительно статора или ротора

96 97
системах координат. В силу периодичности магнитного поля имеем
1
znk
k
BB
. (2.12)
Следовательно, для определения
k
B
необходимо составить
уравнения. Это будут (2Q-1) уравнений равновесия магнитных
контуров, имеющих шаги по расточке соответственно из Q и
единицы счетных точек:
QkkakQkk
FFUUU
, (2.13)
11
kkkk
FFUU
, (2.14)
и одно уравнение непрерывности магнитного потока:
.0
2
0
Q
k
k
B
(2.15)
В формулах (2.13), (2.14)
2
FFFU
i
zkkk
, (2.16)
2
FFFU
i
QkzQkQk
– (2.17)
– магнитные напряжения переходного слоя и полюса индуктора,
приходящиеся на сторону контура со счетной точкой воздушного
зазора соответственно k и ( Qk
);
Qk
k
S
Si
a
i
ak
FU
– (2.18)
– магнитное напряжение части контура с шагом Q,
соответствующим ярму якоря; S
k
- номер зубца якоря, через который
проходит сторона контура со счетной точкой зазора k;
kkfkk
xFxFFF
Д
– (2.19)
– сумма МДС обмоток якоря, возбуждения и успокоительной,
приходящихся на счетную точку зазора k.
В случае, когда пространственный период изменения
магнитного поля составляет
2
(
pzz
11
; имеем обмотку якоря с
целым q или
2Nq
целому числу), в качестве счетных точек
удобно взять точки, принадлежащие первым двум полюсам. Эти
точки удовлетворяют неравенствам:
22
1
R
i
k
x
;
232
2
R
i
k
x
.
2.2.2. Решение исходной системы уравнений (2.13)-(2.15) на ЭВМ
При отсутствии насыщения магнитной цепи, когда
0
2
akzk
UFF
,
исходная система алгебраических уравнений (2.13)-(2.15) является
линейной и может быть решена, при заданных значениях токов
обмоток и углового положения ротора, стандартными численными
методами, например, методом Гаусса. Попытки решений системы
с учетом насыщения магнитной цепи методом Ньютона
применительно к синхронной машине типа СД 102-8 мощностью
75 кВт (открытые пазы на статоре; q =5/2;
1
z
=15; n =2) в
большинстве случаев успеха не имели - для получения решения
требуется знание начального вектора неизвестных сравнительно
хорошего приближения. Наиболее надежно и достаточно просто
этот вектор можно определить методом продолжения решения по
параметру [109]. Исходную систему нелинейных уравнений,
записанную в векторном виде
,Fxf
(2.20)
где
,......
221221
TT
QQ
BBBxxxх
,
f
F
– вектор-функции со-
ответственно левой и правой частей исходной системы, можно
представить также в форме
,T
CFCxf
(2.21)
где
- некоторый вещественный параметр с областью
непрерывного изменения
T
0
;
0
xfC
- значение вектора
f
при произвольном (начальном) векторе
0
xx
.
Как видно из (2.21), переменные
i
x
непрерывно зависят отт
значения параметра
:
ii
xx
; Qi 2,...2,1
, (2.22)
причем решение
0
xx
соответствует значению параметра 0
.
При T
уравнение (2.22) принимает вид (2.20). Очевидно,
решение
Txx
ii
является искомым. В соответствии с теорией о
неявных функциях решение уравнения (2.21) единственно, если
